基于RSSI的改进差分修正加权质心定位算法
2021-06-21余学帆王宏志曹学瑶胡黄水
余学帆, 王宏志, 韩 博, 曹学瑶, 胡黄水
(长春工业大学 计算机科学与工程学院, 吉林 长春 130012)
0 引 言
由大量低成本、低功耗的微型无线传感器节点构成的无线传感器网络(Wireless Sensor Network, WSN)已经广泛应用于环境监测、军事、公共安全等领域[1]。在WSN领域,节点定位技术已经成为WSN研究技术中重要的支撑技术之一[2]。
目前的定位技术根据定位方法可分为两类:基于测距(Range-based)定位算法,通过测量节点间距离或角度,运用三边测量或者三角测量法等,主要包括TOA、TDOA、RSSI[3-5]等,基于非测距(Range-free)定位算法,通过网络连通度来估计未知节点到信标节点的距离或未知节点的坐标,主要包括APIT、DV-Hop以及质心算法等。文献[6]提出一种将路径损耗因子根据实测环境进行动态修正的三边质心定位算法,通过修正路径损耗因子优化RSSI,但在三边定位过程中只计算相交圆交点的均值,没有考虑交点对质心的影响力;文献[7]提出采用最小二乘曲线拟合方法估计发射功率和路径损耗指数,实现优化算法的目的;文献[8]采用卡尔曼滤波对RSSI进行最优化处理,在三边质心的基础上采用加权质心算法提高定位精度,但在求质心时,按顺序取9个距离构建3个距离组合,距离组合间相差较大,增加定位误差;文献[9]根据接收的信号强度设定自适应基准值修正RSSI集合,减少算法的误差与计算量;文献[10]以常态方程代入解得坐标的误差倒数作为权值提高定位准确性;文献[11]采用四边形加权定位结合最小二乘法辅助定位实现精确定位;文献[12-14]在质心定位的基础上引入粒子群算法,通过粒子群算法优化定位结果,但增加了算法的复杂度。
文中提出一种基于RSSI的改进差分修正加权质心定位算法(Improved differential correction weighted centroid location algorithm based on RSSI, IDCL-BR),通过预处理后的RSSI计算信标节点的距离,升序排序后,将前3个距离的质心作为参考节点,通过参考节点与信标节点的位置关系计算差分修正因子,最后对修正后的质心作加权计算未知节点坐标。从节点通信半径、路径损耗因子、信标节点个数等方面对算法进行仿真分析,验证其性能。
1 算法模型
在WSN中,节点通过收发信号传输自身节点坐标及数据。在实际环境中,信号传输会受到多径效应、反射、折射等干扰,从而造成信号衰减。文中采用自由空间传播损耗模型和对数-常态分布模型[15]。
自由空间传播损耗模型
P(d0)=32.4+10klg(d0)+10klg(f),
(1)
式中:P(d0)----信号传播距离为d0的路径损耗;
k----路径损耗因子,取值为[2,5];
f----信号频率。
对数-常态分布模型
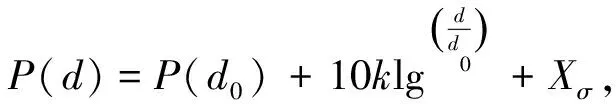
(2)
式中:P(d)----信号传播距离为d的路径损耗;
d0----参考距离,取d0=1 m;
Xσ----均值为0、方差为σ的高斯随机分布函数。
未知节点接收信标节点的信号强度为
RSSI=PS+PA-P(d),
(3)
式中:RSSI----接收信号强度;
PS----信号发射功率;
PA----天线增益。
通过式(1)~式(3)可求未知节点与信标节点的距离d。
2 质心定位算法
2.1 传统质心定位算法
传统质心定位算法是基于节点的连通性,无需测量节点间距离的定位算法。其原理是未知节点接收到通信范围内多个信标节点的广播信号,记录信号内信标节点的ID及坐标等相关信息,并根据多边形的质心算法来估计未知节点的坐标,即

(4)
式中:(x,y)----未知节点坐标;
(x1,y1),(x2,y2),…,(xn,yn)----未知节点通信范围内的信标节点坐标;
n----信标节点数量。
2.2 加权质心定位算法
通过对质心定位算法研究可知,传统质心定位算法实施简单,定位精度误差较大,没有体现出信标节点对未知节点定位的影响力。由未知节点到信标节点间的距离与RSSI值的关系可知,未知节点接收到的RSSI值越大,则未知节点与信标节点距离越近,定位误差越小;反之,RSSI值越小,未知节点与信标节点距离越远,定位误差越大。加权质心定位算法基本原理是通过加权因子来体现信标节点对未知节点定位的影响力。
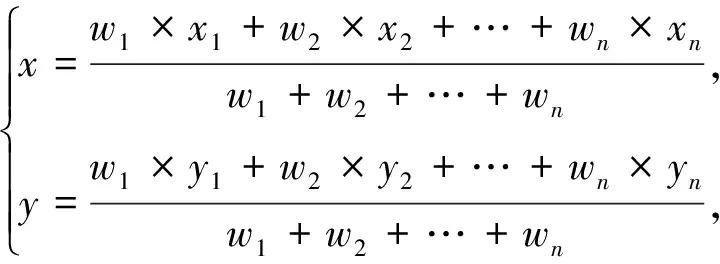
(5)
式中:(x,y)----未知节点坐标;
(x1,y1),(x2,y2),…,(xn,yn)----信标节点坐标;
di----未知节点与信标节点的距离。
3 IDCL-BR算法
3.1 RSSI预处理
未知节点接收到信标节点的广播信号,记录信号对应的信标节点ID、坐标以及RSSI值等信息。但是广播信号在实际传输过程中,受到多径效应、反射、折射等不稳定因素的干扰,未知节点接收的RSSI值误差较大。因此,通过下式对每个信标节点的一组RSSI值进行预处理。

(6)
式中:RSSIi----第i个信标节点的RSSI预处理结果;
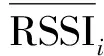

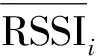

(7)

(8)
式中:m----未知节点接收到每个信标节点的RSSI值样本数。
3.2 质心差分修正
在实际环境中,多径效应、反射、折射等环境因素对RSSI值的影响较大,通过预处理在一定程度上解决了RSSI值的波动问题,直接采用预处理后的RSSI值通过加权质心定位的精度偏低。文中通过预处理后的RSSI值计算信标节点的测量距离与质心,并对质心差分修正以提高定位精度。
假设点O为未知节点,A1(x1,y1),A2(x2,y2),…,An(xn,yn)是未知节点通信范围内的信标节点,由RSSI计算的距离升序排序为{d1,d2,d3,d4,…,dn},取距离{d1,d2,d3},其对应的信标节点为A1、A2、A3,以信标节点A1、A2、A3为圆心,分别以d1、d2、d3为半径画圆,可得到三个圆的重合区域,如图1所示。

图1 三边测量示意图
重合区域的交点为O1、O2、O3,交点O1(xo1,yo1)的坐标由下式可求,
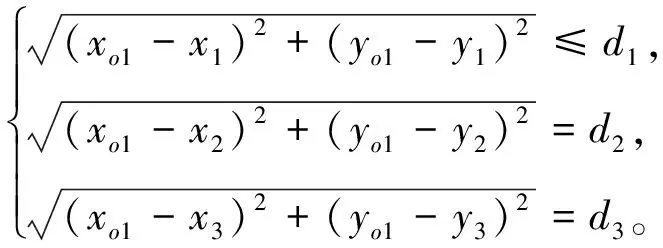
(9)
其中,(xo1,yo1)为交点O1的坐标,同理可求交点O2、O3的坐标(xo2,yo2)、(xo3,yo3),以O1、O2、O3为顶点作三角形,则△O1O2O3的质心M1(xm1,ym1)为

(10)
同理,按顺序逐次取{d2,d3,d4},{d3,d4,d5},…,{dk,dk+1,dn}为半径,距离对应的信标节点为圆心画圆,得到的质心坐标为M2(xm2,ym2),M3(xm3,ym3),…,Mk(xmk,ymk),k=n-2,质心分布如图2所示。
由上文距离排序可知,{d1,d2,d3}对应的三个信标节点离未知节点最近,则其质心M1与未知节点的误差相对于其他质心更小,因此,将质心M1作为参考节点,通过参考节点与信标节点的位置关系计算差分修正因子。信标节点A1,A2,A3,…,An与未知节点的距离为d1,d2,d3,d4,…,dn,信标节点与质心M1距离为d11,d12,d13,d14,…,d1n,则差分修正因子为

(11)
对质心修正

(12)


图2 差分修正示意图
通过对质心坐标的差分修正,减小了质心与未知节点的偏差。利用质心对未知节点进行定位的过程中,距离越近的质心对未知节点坐标确定的影响力越大,可通过质心权值来体现。质心M1由未知节点与信标节点{A1,A2,A3}的测量距离确定,则质心M1权值为
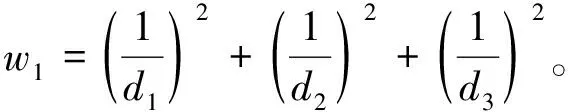
(13)
同理,质心Mi权值为

(14)
未知节点的估计坐标(xbest,ybest)为

(15)
则未知节点的定位误差为

(16)
式中:(xo,yo)----未知节点O的真实坐标;
(xbest,ybest)----未知节点的估计坐标。
若节点通信半径为R,则平均定位误差为

(17)
3.3 算法步骤
1)信标节点周期性广播信号,信号包含其自身的ID及坐标等信息。
2)未知节点接收到多个信标节点信号,记录信标节点的ID、坐标,并对每个信标节点的一组RSSI进行预处理。
3)未知节点通过传播损耗模型计算信标节点的距离,对距离从小到大排序,并建立距离与信标节点的映射。
4)按顺序逐次取三个距离及对应的信标节点,构成如图1所示重合区域,计算重合区域交点以及交点的质心。
5)前三个距离的质心M1作为参考节点计算差分修正因子对其他质心进行差分修正,减少质心的位置偏差。
6)采用加权质心算法对修正后的质心估计未知节点的坐标。
4 仿真分析
为了验证IDCL-BR算法的性能,采用Matlab实验平台,在50 m*50 m的区域内,随机分布25个信标节点与5个未知节点。从节点通信半径、路径损耗因子、信标节点个数三个方面对IDCL-BR算法、传统质心定位算法、三边质心定位算法[6]以及加权质心定位算法[8]进行仿真实验对比分析,为了提高算法的稳定性,进行了30次实验,取30次实验的平均值作为最终结果。
随着节点通信半径变化的平均定位误差仿真结果如图3所示。

图3 不同节点通信半径的平均定位误差
由图3可见,传统质心定位算法采用未知节点通信半径内的信标节点坐标直接估算未知节点坐标,平均定位误差较大。而三边质心定位算法、加权质心定位算法、IDCL-BR算法根据接收信号强度对未知节点进行定位,定位精度明显优于传统质心定位算法。当通信半径为10 m时,IDCL-BR算法平均定位误差高于加权质心定位算法,但随着通信半径的增大,未知节点通信半径范围内的信标节点数量增多,IDCL-BR算法的误差低于其他三种定位算法。当通信半径为30 m时,IDCL-BR算法的平均定位误差只有0.118。
路径损耗因子k的取值为2.0~5.0,由于传统质心定位算法只参考信标节点的位置,路径损耗因子变化不影响传统质心定位算法的精度,所以只对比三个算法随着路径损耗因子变化的平均定位误差仿真结果,如图4所示。
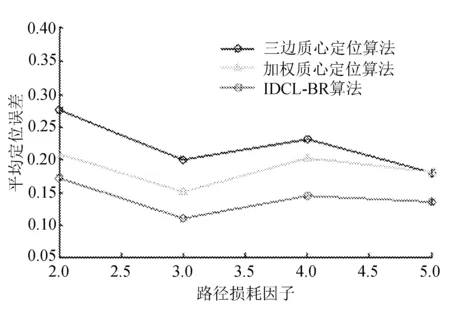
图4 不同路径损耗因子的平均定位误差
由图4可见,IDCL-BR算法优于其他两种算法,并且当路径损耗因子为3.0时,IDCL-BR算法的定位误差最小。
随着信标节点数变化的平均定位误差仿真结果如图5所示。

图5 不同信标节点的平均定位误差
由图5可见,在参与定位的信标节点数量较少的情况下,四种定位算法的定位误差都较大,传统质心定位算法的平均定位误差高达0.493,随着参与定位的信标节点数的增加,定位误差逐渐降低。IDCL-BR算法的定位误差明显低于其他三种算法,当信标节点数为25时,四种算法的定位误差都达到最小,IDCL-BR算法的平均定位误差为0.122,传统质心定位算法的平均定位误差为0.176,三边质心定位算法的平均定位误差为0.146,加权质心定位算法的平均定位误差为0.134。
5 结 语
提出一种基于RSSI的改进差分修正加权质心定位算法,首先对信标节点广播信号的接收强度进行预处理,在一定程度上减小了环境对定位结果的影响;然后采用改进的差分修正质心算法进行定位,采用逐次构建相交圆计算质心,并将第一个质心作为参考节点计算差分修正因子对质心进行修正,减少质心的偏差;最后对修正后的质心作加权处理,以距离的倒数平方和作为权值,降低偏差相对较大质心的影响力,从而提高定位精度。从节点通信半径、路径损耗因子、信标节点数等方面对算法进行仿真分析,IDCL-BR算法在通信半径为30 m,路径损耗因子为3.0,信标节点数为25时,平均定位误差为0.122,该算法相比其他算法,定位精度与稳定性方面更加突出。
