单轴对称十字型钢混凝土柱轴压荷载-变形曲线理论模型及其试验验证

余吉鹏，周天华，李亚鹏，张钰

(长安大学建筑工程学院，陕西西安，710061)

结构设计中，梁、柱中心线宜重合[1]，但由于要满足建筑立面或不均匀受力的要求，实际工程中，常出现梁柱中心线不重合的现象[2]。对于组合结构，为满足建筑立面一侧平齐，型钢混凝土梁中心线偏离型钢混凝土柱中心线，造成组合柱中型钢非对称设置[3-4]，T形、L形和单轴对称十字型钢的配置方式分别适用于边柱、角柱和中柱。一些学者对非对称型钢组合柱结构性能进行了研究[4-11]。曾磊等[7-8]对24个非对称配钢组合柱在低周反复荷载作用下受力性能进行了试验研究，根据塑性下限定理，提出了非对称配钢组合柱压弯承载力计算公式。NISHIMURA 等[9]采用叠加法对T形配钢组合柱受弯性能进行试验和理论研究，提出了该组合柱受弯承载力计算方法。CHEN等[10]以纵筋分布形式、是否配置拉筋、箍筋间距和轴压比为参数，对T形型钢组合构件进行低周往复加载试验，结果表明，T形型钢对构件破坏形态影响较为明显。XIANG 等[11]对T 形型钢混凝土柱在冲击荷载作用下的受力性能进行研究，试验结果表明，该组合柱具有较好的抗冲击性能。上述研究表明，目前关于该类组合柱的研究大部分集中在T形和L形型钢组合柱，缺乏对SRCC-MCS 结构性能的研究。

在型钢约束混凝土本构模型研究方面，El-TAWIL 等[12]对H 型钢约束混凝土受力机理进行了研究，提出了组合柱型钢内混凝土所受约束应力的计算方法。CHEN等[13]对组合柱轴压性能进行理论研究，提出了十字型钢约束混凝土本构模型计算方法。赵宪忠等[14]结合试验和理论研究，建立了十字型钢约束混凝土应力-应变曲线计算方法。综上可知，关于型钢约束混凝土本构模型大多是基于H 型钢和十字型钢建立的，而对非对称型钢约束混凝土本构模型的研究较少。鉴于此，本文以SRCC-MCS 为研究对象，根据箍筋和型钢的约束范围，划分SRCC-MCS 截面约束区，分析型钢对混凝土的约束机制，借鉴Mander 约束混凝土模型[15]，提出不同约束区混凝土应力-应变曲线，基于静力平衡及应变协调，建立该组合柱荷载-变形曲线理论模型和简化计算模型，并进行试验验证，为后续该类组合柱研究提供理论支持。

1 SRCC-MCS 轴压荷载-变形曲线理论模型

轴压荷载作用下，SRCC-MCS 混凝土膨胀变形，钢筋和型钢限制混凝土变形的发展，从而使混凝土强度和变形能力得到提高[12-15]，SRCC-MCS的轴压性能增强。根据箍筋和型钢的约束范围，划分SRCC-MCS 截面约束区[14]，SRCC-MCS 截面可分成非约束区、部分约束区、型钢弱约束区、型钢强约束区、纵筋、型钢翼缘和腹板7部分，如图1所示。

图1 SRCC-MCS截面约束区划分Fig.1 Regional partition of the concrete of SRCC-MCS

1.1 非约束混凝土和部分约束混凝土应力-应变曲线

矩形箍筋有效约束区如图2所示，图中，bc为箍筋x方向中心线之间的距离；dc为箍筋y方向中心线之间的距离；w'i和s′分别为相邻纵筋和箍筋之间的净距；s为箍筋间距。Mander 约束混凝土应力-应变模型[15]为

图2 矩形箍筋有效约束区Fig.2 Effectively confined core for rectangular stirrup

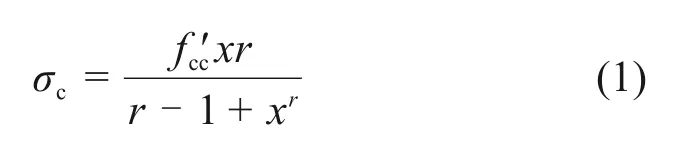
其中：

式中：r和x为参数；σc，εc和f'cc分别为约束混凝土应力、应变和强度；εcc和Esec分别为约束混凝土峰值应变和割线模量；εco，Ec和fco分别为混凝土峰值应变、切线模量和强度[15]。

部分约束混凝土受箍筋x方向和y方向有效侧向约束应力分别为[15]：

其中，箍筋有效约束系数ke为：

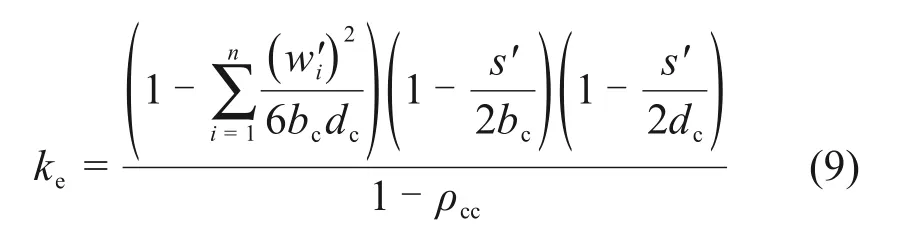
式中：ρx为箍筋x方向中心线之间的配箍率；ρy为箍筋y方向中心线之间的配箍率；ρcc为部分约束区配筋率；fyh为箍筋屈服强度。

有效约束应力与混凝土强度提高系数关系如图3所示，其中，fl为有效侧向约束应力；flx和fly分别为x方向和y方向有效侧向约束应力。由图3可得到部分约束混凝土强度提高系数Kp，则部分约束区混凝土强度fpc为

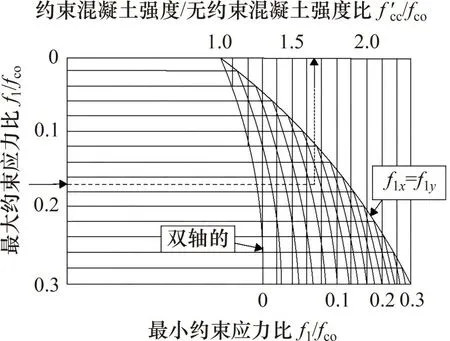
图3 有效约束应力与混凝土强度提高系数关系Fig.3 Relationships between effective confining stress and coefficient of strength enhancement

非约束混凝土不受约束作用，因此，非约束混凝土强度fuc=fco。由式(1)～(6)可得非约束混凝土和部分约束混凝土应力-应变曲线，如图4所示，其中，ε'pc为部分约束区混凝土峰值应变。

图4 非约束和部分约束混凝土应力-应变关系Fig.4 Stress-strain relations of unconfined concrete and partly confined concrete

1.2 型钢弱约束和强约束混凝土应力-应变曲线

以SRCC-MCS芯柱1/4截面为研究对象分析型钢对混凝土的约束机制。SRCC-MCS 芯柱截面如图5所示，其中，B和tf分别为翼缘长度和厚度；tw为腹板厚度；H为水平腹板长度。

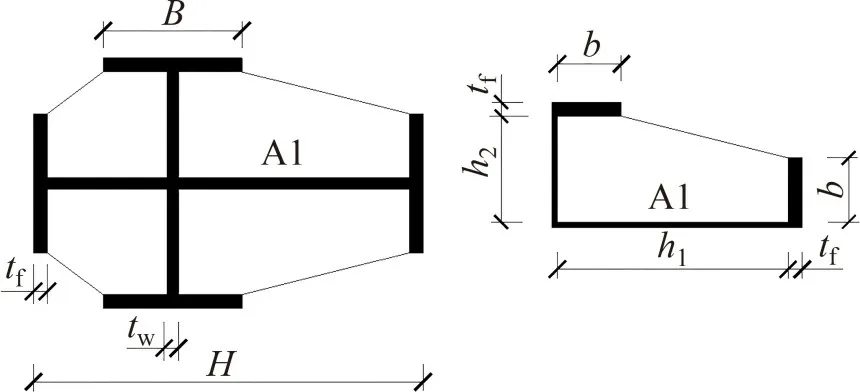
图5 SRCC-MCS芯柱截面Fig.5 Cross section of SRCC-MCS core column

SRCC-MCS芯柱1/4截面型钢真实约束应力分布状态如图6(a)所示，其中，fl,s为型钢侧向约束应力。由图6(a)可知，型钢对混凝土的约束应力大部分集中在翼缘AB和CD段、腹板EF和FG段，而腹板AG与ED段侧向约束应力相对较小。为便于分析，简化约束应力分布，如图6(b)所示，不考虑AG和ED段约束应力，再将其余各段约束应力等效成均匀分布[14,16]。

图6 SRCC-MCS芯柱约束应力简化模型Fig.6 Simplified state of lateral confining stress of SRCC-MCS core column

根据上述分析可将SRCC-MCS芯柱1/4截面分为型钢无约束区、弱约束区和强约束区，各型钢约束区混凝土受力状态如图7所示。

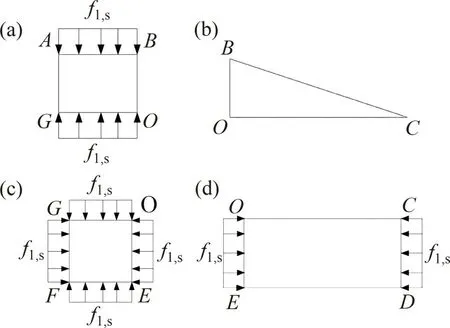
图7 各约束区混凝土简化约束状态Fig.7 Simplified stress state of each confined concrete region

根据SRCC-MCS 芯柱1/4 截面约束区的划分，SRCC-MCS芯柱约束区划分如图8所示。

图8 SRCC-MCS芯柱约束区划分Fig.8 Regions for SRCC-MCS core column

轴压荷载下，SRCC-MCS 混凝土膨胀变形，翼缘外伸段发生弯曲变形，将外伸段等效成悬臂梁[16]，则外伸段受力状态如图9所示。其中，外伸段所受的力矩Mu为

图9 翼缘受力状态Fig.9 Stress state of flange

式中：b为外伸段长度。

试件达到极限状态时，外伸段根部达到屈服(图9)，则外伸段截面抵抗矩M'u为[16]：

式中：fyf为翼缘屈服强度。

由式(11)和(12)可得翼缘侧向约束应力fl,s为

参考箍筋有效侧向约束应力计算方法[15]，计算翼缘有效侧向约束应力fl,es：

其中，型钢有效约束系数ke,s为[15]：

式中，Aec和Acc分别为型钢有效约束区和约束区的混凝土面积。

MIRZA[17]在定义H型钢有效约束区时，认为H型钢有效约束区边界为抛物线，且抛物线与型钢翼缘的切线倾角为45°，如图10所示。

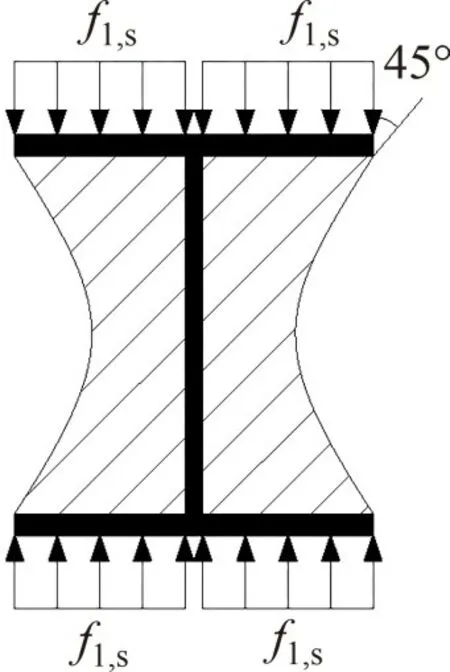
图10 H型钢混凝土有效约束区Fig.10 Region for H-shaped steel effectively confined concrete

为便于分析，将SRCC-MCS芯柱1/4截面等效成2个1/2 H型钢截面[16]，分别计算2个方向有效约束系数，借鉴H型钢有效约束区划分方法[17]，划分1/2 H型钢有效约束区，如图11所示。

图11 混凝土有效约束区Fig.11 Effective region of confined concrete

由式(15)可得SRCC-MCS 芯柱1/4 型钢截面在x和y方向有效约束系数ke,sx和ke,sy分别为：

式中：h1和h2分别为型钢腹板在x和y方向净长度。

型钢和箍筋对Ⅰ区混凝土(图8)在x方向和y方向的复合有效侧向约束应力fle,hx1和fle,hy1分别为[12]：

其中，fle,sx1和fle,sy1分别型钢对Ⅰ区混凝土2个方向施加的有效侧向约束应力。

由图4可得Ⅰ区约束混凝土强度提高系数Kh1，则Ⅰ区约束混凝土强度为：

同理，可得SRCC-MCS 芯柱各约束区混凝土强度，由式(1)～(6)得到不同约束区混凝土应力-应变曲线，如图12所示。图中，ε′sc1，ε′sc2，ε′sc3，ε′sc4和ε′sc5分别为Ⅰ～Ⅴ区混凝土对应的峰值应变；fsc1，fsc2，fsc3，fsc4和fsc5分别为Ⅰ～Ⅴ区混凝土对应的峰值应力。

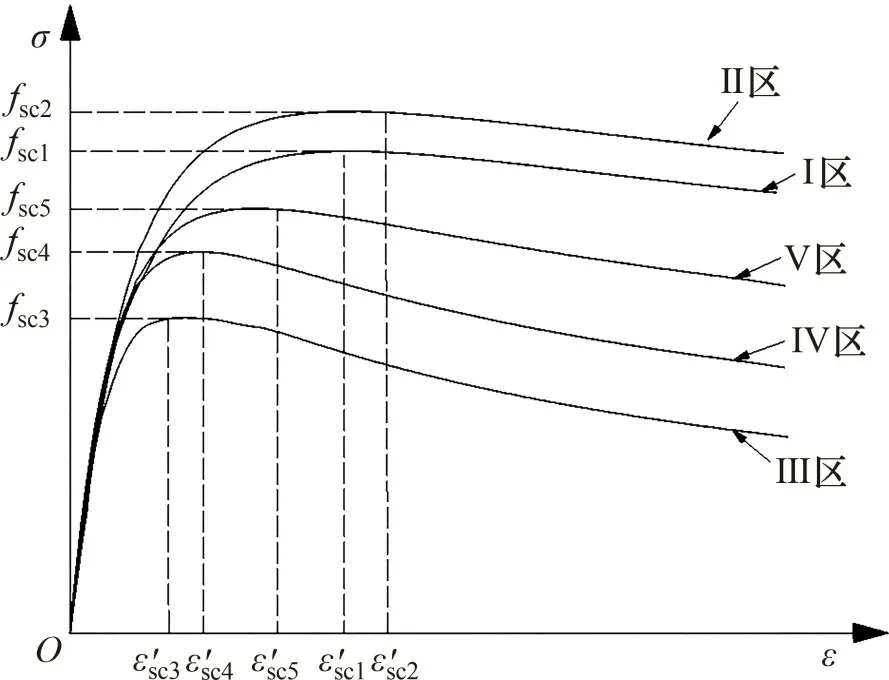
图12 不同约束区混凝土应力-应变曲线Fig.12 Stress-strain curves of different steel confined concrete

对于工程中常见的T形和L形型钢，可采用本文提出的型钢混凝土约束区划分方法(图13)，计算不同型钢约束区有效约束系数，然后基于Mander约束混凝土本构模型，得到各型钢约束区混凝土应力-应变曲线。

图13 芯柱约束区划分Fig.13 Regions for core columns

1.3 纵筋应力-应变曲线

采用文献[13]提出的钢筋简化应力-应变曲线研究纵筋应力-应变关系，如图14所示。由图14可见，当应变达到纵筋屈服应变εyr，纵筋强度达到屈服强度fyr；当应变达到非约束混凝土峰值压应变εco，认为混凝土保护层剥落，纵筋出现局部屈曲，应力开始下降；当应变达到4εco，纵筋应力下降到0.2fyr，应变继续增大，应力保持不变。

图14 纵筋应力-应变关系Fig.14 Stress-strain relation of longitudinal bar

1.4 型钢应力-应变曲线

轴压荷载使组合柱混凝土产生横向变形，则型钢腹板水平受拉(图9)，根据静力平衡可得型钢腹板受到的拉应力σst为

由于型钢腹板处于拉压双向应力状态，根据“双向应力椭圆理论”得[13]

式中：σsv为腹板轴向应力；fyw为腹板屈服强度。

由式(22)可得双向应力状态下，型钢腹板达到屈服强度时腹板轴向应力fyv,w，同时，考虑钢材的应变硬化[13]，其中，钢材硬化段斜率Esh为

式中：εy和εu分别为钢材屈服应变和极限应变；fy和fu分别为钢材屈服强度和极限强度。

型钢腹板和翼缘应力-应变曲线如图15所示，图中，Esh,f和Esh,w分别为型钢翼缘和腹板硬化段斜率；εyv,f为翼缘屈服应变；εyv,w为腹板轴向应力达到fyv,w时的应变。

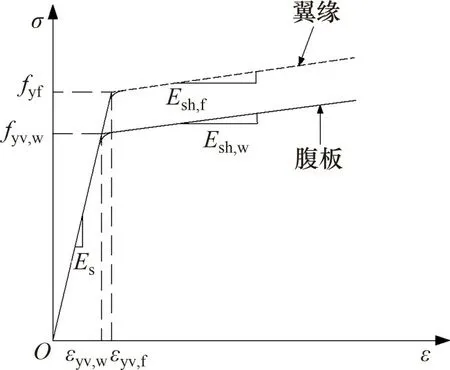
图15 翼缘和腹板应力-应变关系Fig.15 Stress-strain relation of steel flange and web

1.5 荷载-变形曲线理论模型的建立

计算SRCC-MCS荷载-变形曲线时，基本假定如下：

1)混凝土和型钢无相对滑移。

2)组合柱各部分采用本文建立的应力-应变曲线。

3)不考虑长细比的影响。

基于以上假定，将SRCC-MCS 轴压承载力N分成10 部分承载力叠加，分别为翼缘、腹板、纵筋、非约束混凝土、部分约束混凝土、型钢强约束混凝土(Ⅰ和Ⅱ区)和型钢弱约束混凝土(Ⅲ，Ⅳ和Ⅴ区)。根据静力平衡和变形协调[18-19]，可得：

式中：N为组合柱轴压承载力；σuc和Auc分别为非约束混凝土轴向应力和截面面积；σpc和Apc分别为部分约束混凝土轴向应力和截面面积；σsc1，σsc2，σsc3，σsc4和σsc5分别为Ⅰ～Ⅴ区混凝土轴向应力；Asc1，Asc2，Asc3，Asc4和Asc5分别为Ⅰ～Ⅴ区混凝土截面面积；Ar，Aaw和Aaf分别为钢筋、腹板和翼缘截面面积；σr，σaf和σaw分别为钢筋、翼缘和腹板轴向应力；εuc，εpc，εr，εaf和εaw分别为非约束混凝土、部分约束混凝土、钢筋、翼缘和腹板轴向应变；εsc1，εsc2，εsc3，εsc4和εsc5分别为Ⅰ～Ⅴ区混凝土轴向应变。

荷载-变形曲线计算流程如图16所示。具体步骤如下。

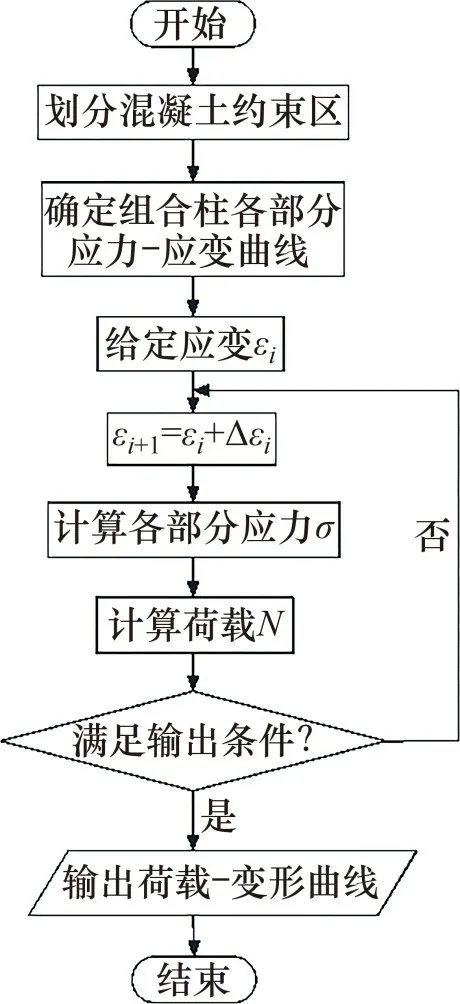
图16 荷载-变形曲线计算流程图Fig.16 Calculation flow chart of load-deformation curve

步骤1)给定初始轴向应变ε1，由上述10 部分应力-应变关系可得各部分应力，由式(24)可得荷载-变形曲线上对应的第1点。

步骤2)给定初始应变增量Δε1，可得第2 个点轴向应变为ε2=ε1+Δε1，重复步骤1)，得到曲线上第2点，依次进行，得到荷载-变形全过程曲线。

1.6 荷载-变形曲线简化模型

为便于应用，参考文献[20]中组合柱轴压荷载-变形曲线简化方法，建立了SRCC-MCS 荷载-变形曲线简化模型，如图17所示。该模型可分成弹性段和下降段2 个阶段，其中，弹性段刚度EA为[21]：

图17 轴向荷载-变形曲线简化模型Fig.17 Simplified calculation model of axial loaddeformation curve

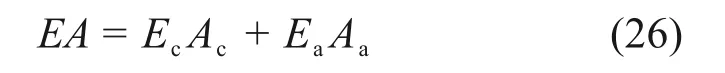
式中：EcAc为钢筋混凝土部分截面轴向刚度；EaAa为型钢截面轴向刚度。Ec和Ea分别为钢筋混凝土和型钢部分弹性模量；Ac和Aa分别为钢筋混凝土和型钢部分面积。

则弹性段斜率ke为[20]：

式中：H组合柱高度。

采用叠加法计算SRCC-MCS 轴压承载力Nm[16]为

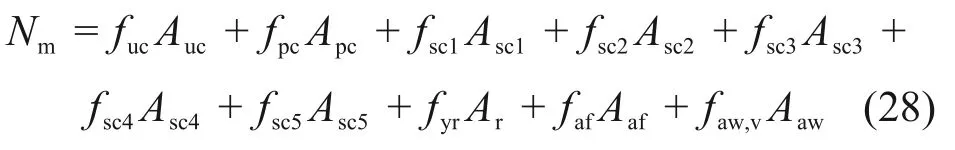
峰值点位移Δm为

参考文献[20]，下降段斜率kd为

极限荷载Nu为

则极限变形Δu为极限荷载Nu对应轴向变形。

2 试验验证

2.1 SRCC-MCS截面特征

SRCC-MCS 截面物理形心位置，对研究其轴压性能影响显著。如图18所示，图中Oa为偏心H型钢对称轴，Oc和Om分别为SRCC-MCS截面几何和物理形心轴[22]，则Oa轴之间的Oc轴的距离ea为十字型钢偏心距。

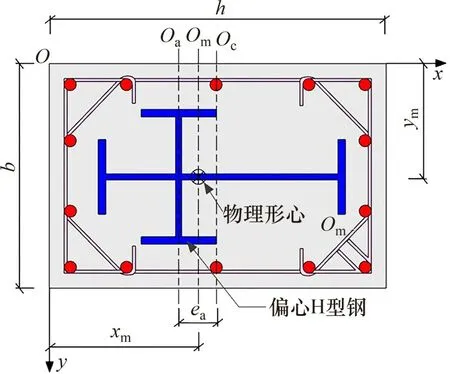
图18 SRCC-MCS截面特征Fig.18 Section feature of SRCC-MCS

参考文献[4]中方法，将混凝土面积按强度等效原则换算成钢材面积，然后计算SRCC-MCS 截面物理形心位置，即[4]

式中：xc，xr，xaw和xaf分别为混凝土、纵筋、腹板和翼缘形心横坐标；Ac为混凝土截面面积。

2.2 试验概况

以十字型钢偏心率(ea/h)、配钢率(ρa)、箍筋间距(s)和混凝土立方体抗压强度(fcu)为参数，共设计了9 个试件，其中，1 个为SRCC-CS 试件，8 个为SRCC-MCS 试件，试件具体设计参数见表1，表中，h为柱截面长度。试件截面尺寸及配筋按JGJ 138—2016[21]进行设计，其中，试件长×宽×高为450 mm×300 mm×900 mm，型钢采用不同厚度的Q235B 钢板焊接，纵筋采用HRB400 螺纹钢C16，配筋率为2.08%，箍筋和八字形拉筋采用HRB335螺纹钢B12，试件截面尺寸及配筋如图19所示。试验采用C30，C40和C50 3种强度等级的混凝土，混凝土标准立方体试块实测抗压强度平均值见表1，钢材性能实测结果见表2。

表2 钢材实测性能Table 2 Material properties of steel

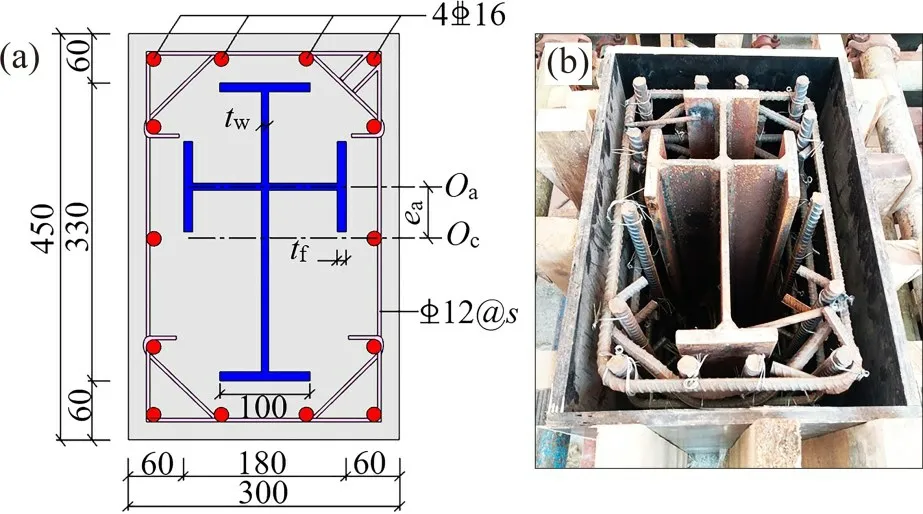
图19 SRCC-MCS配筋形式Fig.19 Construction from of SRCC-MCS

试验在30 MN 电液伺服液压机上进行，试验加载装置如图20(a)所示。在柱两端设置夹具，防止柱端提前破坏。加载前，根据混凝土及钢材力学性能测试结果，确定不同SRCC-MCS 试件物理形心(表1)，将柱截面物理形心与试验机加载板中心对齐，使组合柱轴心受压。加载程序采用位移控制，按0.3 mm/min 的加载速率进行加载，当柱承载力下降至峰值荷载的60%，结束加载[16]。

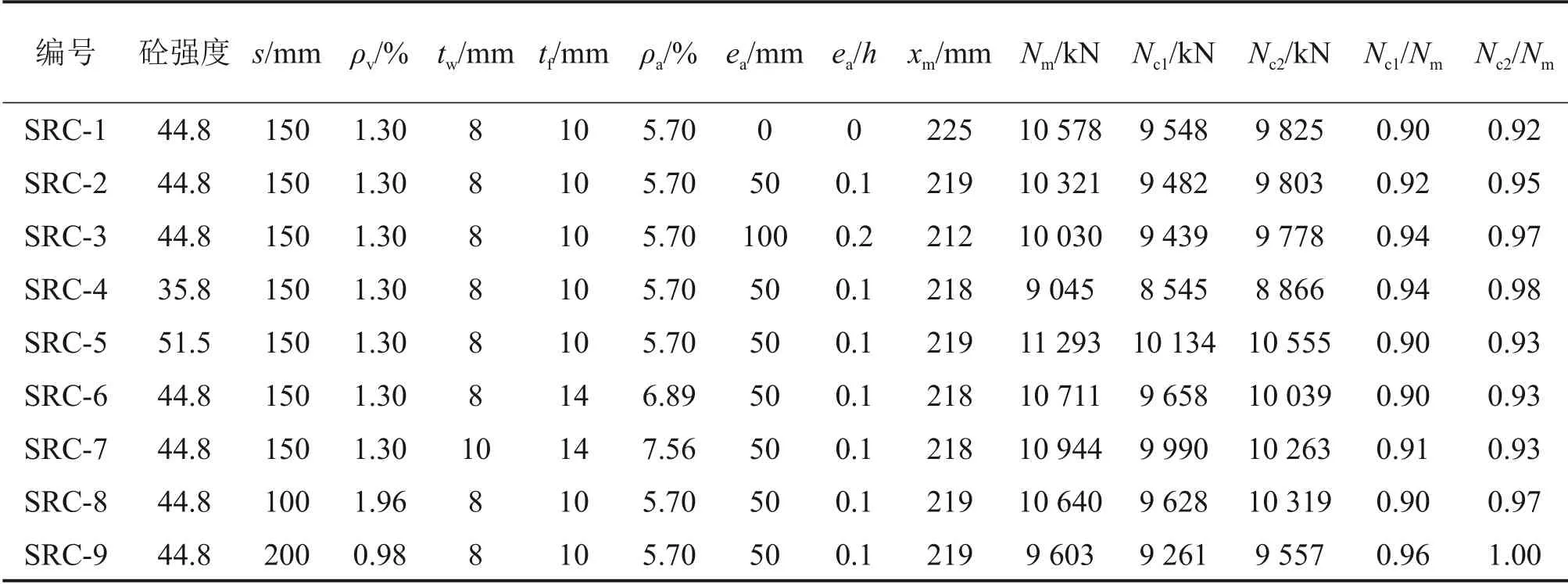
表1 试件参数及试验结果Table 1 Variables and test results of specimens

位移计和应变片布置位置如图20所示，其中，在试件加载端和固定端各布置2 个位移计(D1～D4)量测试件轴向变形，在柱跨中截面粘贴钢筋应变片(Z1～Z3)、型钢应变片(Y1～Y6 和F1～F2)、箍筋应变片(G1～G3)和混凝土应变片(H1～H3)，以量测组合柱各部分应变发展情况。

图20 加载装置及位移计和应变片布置位置Fig.20 Test set-up and position of displacement gauge and strain gage

2.3 试验现象和结果

2.3.1 破坏过程及模式

对于SRCC-CS 试件SRC-1，加载前期，未发现混凝土产生裂缝。荷载达到峰值荷载80%左右时，柱上端出现竖向裂缝，加载位移增大，裂缝发展缓慢，型钢逐渐屈服，箍筋应变增长速率加快。当荷载增加至峰值荷载90%左右时，柱表面裂缝发展迅速，纵筋开始屈服，混凝土起皮剥落，柱达到峰值荷载。加载位移增大，荷载逐渐降低，混凝土大块剥落，纵筋压屈，箍筋向外弯曲变形，试件典型破坏形态如图21所示。由图21(d)可知，试件SRC-1中间截面型钢翼缘轻微压屈。

SRCC-MCS 试件破坏现象及形态大致相同，采用试件SRC-2 介绍SRCC-MCS 系列试件破坏过程。加载前期，混凝土表面未见裂缝。当荷载达到峰值荷载的80%左右时，型钢开始屈服，偏心H型钢对侧柱表面出现竖向裂缝，加载位移增大，裂缝迅速发展。当荷载达到峰值荷载90%左右时，纵筋进入屈服阶段，偏心H 型钢对侧竖向裂缝宽度不断增大，该处混凝土起皮剥落，柱荷载达到峰值。加载位移增加，荷载迅速下降，加载后期，荷载下降缓慢，偏心H 型钢对侧纵筋开始压屈，试件典型破坏形态如图21所示。由图21(e)可知，试件SRC-2 偏心H 型钢对侧型钢翼缘出现轻微局部屈曲。

图21 试件破坏形态Fig.21 Failure modes of specimens

通过比较试件SRC-1 和SRC-2 破坏形态可知，试件SRC-1 破坏整体比较均匀，而试件SRC-2 破坏大部分集中在偏心H型钢的对侧。

2.3.2 应变分析

1)型钢应变分析。典型试件荷载-型钢翼缘应变曲线如图22所示。由图22可见，加载过程中，试件SRC-1不同位置型钢翼缘应变发展规律相同，当荷载增加到峰值荷载的80%左右时，不同位置型钢翼缘应变约为1 900×10-6，达到屈服应变。对于试件SRC-2，当荷载增加到峰值荷载的80%左右时，翼缘应变加速增长，但Y1，Y2 和Y3 处应变增长速率存在差异，Y3 处应变增长较快，先达到屈服应变，试件达到峰值荷载时，Y1 处应变为2 094×10-6，也达到屈服应变，说明型钢的强度得到充分利用。

图22 型钢翼缘荷载-应变曲线Fig.22 Load-strain curves of flange

2)箍筋应变分析。典型试件箍筋荷载-应变曲线如图23所示。由图23可见，加载初始阶段，SRC-1箍筋应变基本保持不变，说明其对混凝土约束作用未发挥。当荷载增加到峰值荷载的80%左右时，箍筋G2处应变增长迅速，先达到屈服，原因是组合柱矩形箍筋长边方向抗弯刚度相对较小。试件达到峰值荷载时，箍筋G1 和G3 处应变约为2 400×10-6，都达到屈服。对于试件SRC-2，当荷载增加到峰值荷载的80%时，箍筋G3处应变增长速率比应变G1处的大。但达到峰值荷载时，箍筋G1处应变约为1 500×10-6，基本达到屈服，这是因为型钢对混凝土的约束应力大部分集中在偏心H型钢的近侧[16]，该处混凝土膨胀变形较小。

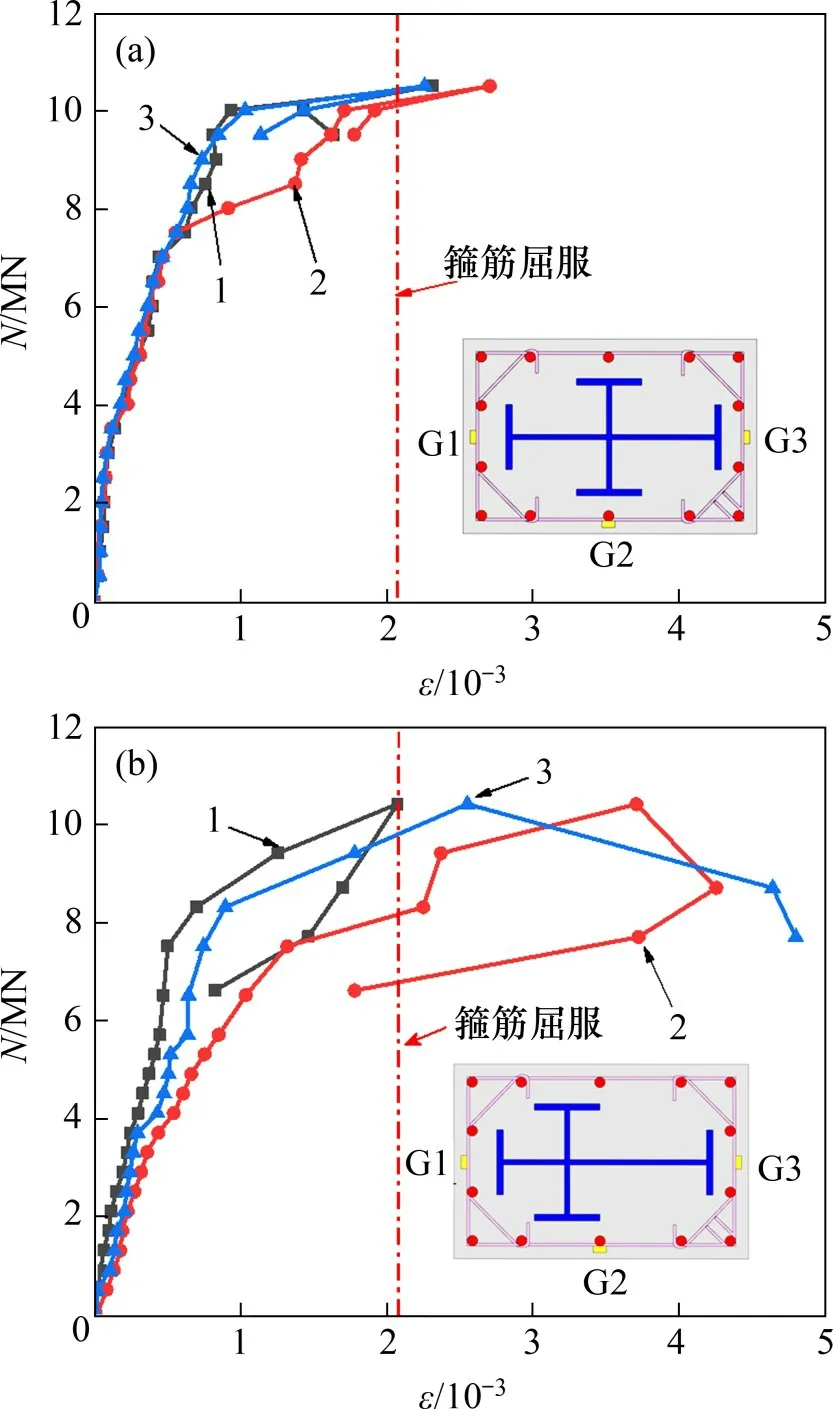
图23 箍筋荷载-应变曲线Fig.23 Load-strain curves of stirrup

2.3.3 轴压荷载-变形曲线

试件轴压荷载-变形曲线如图24所示，试件峰值荷载见表1。由图24和表1可得：

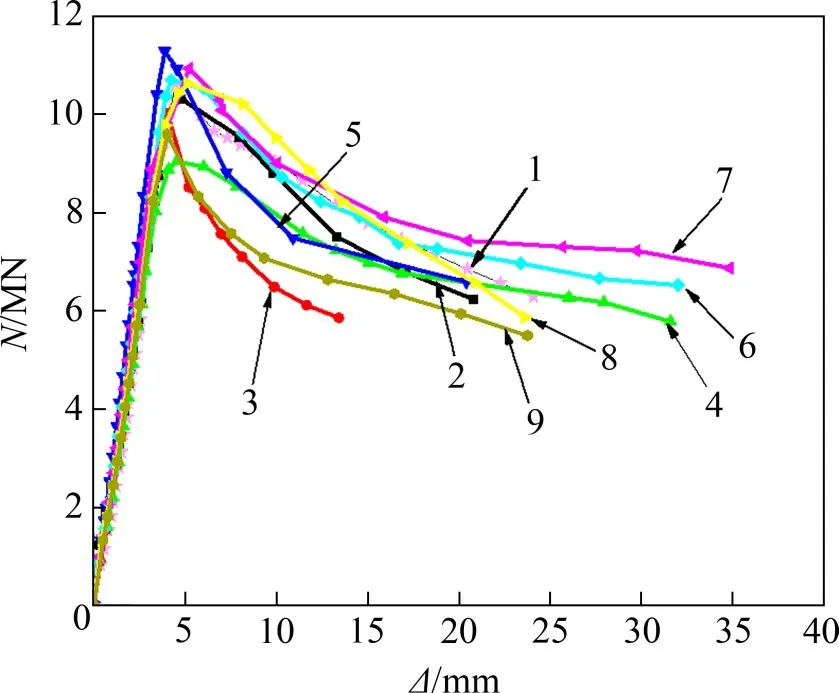
图24 试件荷载-变形曲线Fig.24 Load-deformation curves of samples

1)当十字型钢偏心率ea/h从0增加到0.1，试件SRC-1承载力(峰值荷载Nm)比SRC-2的承载力下降了2.43%；当ea/h从0.1 增加到0.2，试件SRC-2 承载力比SRC-3的承载力下降了2.81%，说明提高十字型钢偏心率，试件承载力降低，这是因为型钢对混凝土的约束作用主要集中在偏心H 型钢近侧[14]，十字型钢偏心率越大，型钢对混凝土的约束作用越不明显[23]，试件后期变形能力下降。

2)当混凝土立方体抗压强度fcu从35.8 MPa 上升到44.8 MPa 时，试件承载力上升了14.09%；当fcu从44.8 MPa 上升到51.5 MPa 时，试件承载力上升了9.42%，表明混凝土强度提高，试件承载力上升，而试件后期变形能力降低，原因是混凝土强度越高，其脆性越大，箍筋和型钢的约束作用越难发挥。

3)当配钢率ρa由5.7%增加到6.89%，试件承载力从10 321 kN 提高到10 711 kN，上升了3.78%；当ρa从6.89%增加到7.56%，试件承载力从10 711 kN 提高到10 944 kN，上升了2.18%，说明提高截面配钢率，组合柱轴压承载力上升，同时可以提高该组合柱后期变形能力。

4)当箍筋间距s从100 mm提高到150 mm，试件承载力由10 640 kN 减小到10 321 kN，降低了3.0%；当s从150 mm提高到200 mm，试件承载力由10 321 kN 减小到9 603 kN，降低了6.96%，说明箍筋间距增大对试件轴压性能产生不利影响，箍筋间距增大，试件承载力减小，后期变形能力下降，原因是增大箍筋间距，箍筋对混凝土的约束作用减小[15]。

2.4 结果验证

图25所示为采用式(24)和(28)计算的试件荷载-变形曲线与试验曲线的对比，表1所示为采用上述2 种方法计算的试件峰值荷载与试验值的比较。由图25可知，采用上述2 种方法计算的试件荷载-变形曲线与试验曲线基本吻合。由表1可知，采用式(24)计算的试件峰值荷载Nc1与试验值Nm比值的均值为0.92，变异系数为0.026，说明提出的型钢约束混凝土应力-应变关系可较好地预测该组合柱荷载-变形全过程曲线；同时，采用式(28)简化模型计算的试件峰值荷载Nc2与试验值Nm比值的均值为0.95，变异系数为0.029，表明建立的SRCC-MCS 轴压荷载-变形曲线简化模型较为合理，可为该组合柱理论分析提供参考。

图25 荷载-变形计算曲线与试验曲线对比Fig.25 Comparison of load-deformation curves between calculation and experiment

3 结论

1)根据箍筋和型钢的约束范围，把SRCCMCS 截面分成7 部分，参考Mander 约束混凝土模型，建立不同的约束区混凝土应力-应变曲线，基于静力平衡和变形协调，得到SRCC-MCS荷载-变形曲线理论模型和简化模型。

2)轴压试验结果表明，SRCC-CS 试件破坏较为均匀，而对于SRCC-MCS 试件，偏心H 型钢对侧混凝土压溃剥落较为严重，该处型钢翼缘及纵筋发生局部屈曲。SRCC-MCS 试件达到峰值荷载时，型钢、纵筋和箍筋均达到屈服。十字型钢偏心率提高，试件承载力和后期变形能力下降。混凝土立方体抗压强度提高，试件承载力大幅提高，而变形能力显著降低。随着配钢率上升，试件承载力和变形能力小幅提高。箍筋间距提高，试件承载力和变形能力降低。

3)采用理论模型和简化模型2种方法计算的试件荷载-变形曲线与试验曲线吻合较好，证明了提出的荷载-变形曲线理论模型和简化模型的正确性。