大埋深隧洞泥质粉砂岩的三轴蠕变试验与理论分析

林韩祥，张强勇，张龙云，向文，丁炎志，张振杰

(1.山东大学岩土与结构工程研究中心，山东济南，250061；2.山东大学齐鲁交通学院，山东济南，250061)

流变理论是岩体力学的重要组成部分，与工程的安全稳定和服务时间紧密相关。大量工程实践表明，岩体工程的破坏与失稳，在许多情况下并不是在开挖完成后立即发生的，它是岩体的应力、变形随时间变化而不断发展和调整，需要延续一段时期[1]。原位测试及试验表明，岩石并不是理想的线性体，其本构关系也是非线性的[2-6]。因此，建立合适的蠕变本构模型来描述岩石的流变力学特性是目前流变力学理论需要研究的重要课题。目前，国内外学者从元件组合模型角度研究岩石的蠕变本构模型已取得了丰硕的研究成果[7-9]。徐卫亚等[10-12]提出一个新的非线性黏塑性元件(NVPB 模型)并与五元件线性黏弹性体串联得到河海模型，可以充分地描述绿片岩加速流变特性。杨文东等[13]研究了大岗山水电站坝基辉绿岩的流变特性，建立了由瞬弹性Hooke 体、黏弹塑性村山体、非线性黏性元件串联组成的岩石非线性黏弹塑性流变模型。张治亮等[14]通过室内岩石三轴蠕变试验研究了向家坝水电站坝基挤压破碎带砂岩的蠕变力学特性，并建立了一个新的岩石六元件非线性黏弹塑性蠕变模型。屈丽娜[15]将非线性黏弹塑性体与伯格斯体串联，得到了改进的非线性伯格斯模型，发现煤样加速蠕变过程中应变加速度与时间成正比的关系，通过河南焦煤集团九里山矿煤样试件蠕变试验曲线验证并取得了理想的试验结果。曹树刚等[16]对西原模型中牛顿黏壶的黏性系数进行改进，所得理论曲线与岩石实际蠕变曲线吻合度较高，较好地反映了岩石的非衰减蠕变特性。康永刚等[17]利用非牛顿黏壶Kelvin模型、非牛顿黏壶粘塑性体与弹簧串联，给出一种改进的岩石黏弹塑性本构关系及对应的蠕变函数，蠕变试验数据进行了较好地描述。

尽管国内外学者针对岩石的蠕变特性开展了大量研究，但目前针对埋深1 km 以上引水隧洞泥质粉砂岩的非线性蠕变力学特性的研究鲜有报道。鉴于此，本文基于三轴蠕变试验结果，从非线性流变力学理论出发，建立一种非线性黏弹塑性模型(NVEPB 蠕变模型)来反映对大埋深隧洞泥质粉砂岩的流变力学特性。研究成果可为工程设计施工和长期运行稳定分析提供了理论指导。

1 大埋深隧洞泥质粉砂岩三轴蠕变试验

1.1 工程概况

香炉山隧洞位于我国云南省境内，起于丽江市玉龙县石鼓镇水源地，止于大理白族自治州鹤庆县松桂镇，全长63.426 km，最大埋深1 512 m，最大洞径9.8 m，是滇中引水工程的控制性重点工程。香炉山隧洞埋深大，地应力较高，地质条件复杂，洞区岩性主要为泥质粉砂岩，采用钻爆法和TBM 组合施工[18-19]。为分析泥质粉砂岩对大埋深隧洞围岩稳定的影响，通过现场深部取样，首先在室内开展泥质粉砂岩的三轴蠕变试验。

1.2 蠕变试验方案

根据国际岩石力学学会(ISRM)试验规程，将现场钻取的深部泥质粉砂岩岩芯运回室内进行切割打磨，加工成直径×长度为50 mm×100 mm 的标准圆柱体。为消除试件微细观缺陷对试验结果的影响，需要对制备的岩石试件进行超声波测试，以选取波速相近的岩样进行蠕变试验。采用山东大学与长春朝阳试验厂联合研制的RLW-1000G岩石三轴蠕变仪进行不同围压分级加轴压三轴蠕变试验，试件围压采用洞区实测的水平应力20 MPa，轴压根据自重应力分级施加，共分7级荷载(19.37，25.46，31.55，37.64，43.73，49.82 和52.86 MPa)。在试验过程中，先以0.5 MPa/s 的速率施加围压，待围压稳定后，再以100 N/s 的速率施加轴向荷载，待变形稳定后，继续施加下一级荷载，直至试样发生破坏为止，本次蠕变试验共历时约320 h。

1.3 蠕变试验结果分析

图1所示为泥质粉砂岩在围压20 MPa 条件下的分级加轴压蠕变曲线；根据图1采用Boltzmann叠加原理处理得到的各级应力水平下的蠕变曲线如图2所示，围压20 MPa 分级加轴压蠕变试验结果如表1所示。

图1 泥质粉砂岩分级加载蠕变试验曲线Fig.1 Creep test curve of argillaceous siltstone under graded loading

图2 各级应力水平下的蠕变曲线Fig.2 Creep curves at each level of stress

表1 围压20 MPa分级加轴压蠕变试验结果Table 1 Creep test results under pressure of axial compression under graded loading when confining pressure is 20 MPa

由图1、图2和表1可知：

1)在不同应力水平下，泥质粉砂岩均具有显著的瞬时变形，蠕变特征的差异也十分明显。

2)岩石蠕变存在门槛效应。当应力水平不超过31.55 MPa时，流变效应不太显著，仅存在衰减蠕变阶段，减速蠕变阶段的蠕变速率趋近于0。当应力水平超过31.55 MPa以后，蠕变效应逐渐显现出来，开始出现稳定蠕变阶段，等速蠕变速率趋近于恒定正值，这表明围压在20 MPa 时，蠕变门槛值为31.55 MPa。

3)当应力水平超过蠕变门槛值时，泥质粉砂岩的等速蠕变速率随着应力水平的提高而不断增大，在最后一级破裂应力作用下，等速蠕变速率达到最大值。

4)当应力水平达到52.86 MPa时，泥质粉砂岩经历短暂的等速蠕变阶段后约在25.19 h 时发生加速蠕变。这表明当应力水平超过泥质粉砂岩的长期强度时，岩石经历减速、等速蠕变阶段后会很快进入加速蠕变阶段。在此过程中，岩石由黏弹性流动发展转化为黏塑性流动。

2 泥质粉砂岩的非线性黏弹塑性蠕变模型(NVEPB蠕变模型)

2.1 蠕变模型辨识

根据前面的蠕变试验结果可知，在进行泥质粉砂岩的蠕变模型辨识时应考虑如下特点：

1)每级荷载(偏应力)作用的瞬时会立即产生瞬时应变，因此，辨识模型中应存在弹簧元件即Hooke体；

2)围压、偏应力保持不变，岩样的应变继续增加，表现出弹性后效的性质，因此，辨识模型中应存在黏性元件即Newton体；

3)当应力较低时，蠕变曲线仅存在减速蠕变阶段，且蠕变速率不断降低，最终趋于0；应力水平较高时，蠕变速率趋于某恒定正值，因此，辨识模型中应存在开关元件[20]；

4)当应力继续不断提高直至超过一定值时，出现加速蠕变阶段，因此，辨识模型中应存在塑性元件即理想塑性体。

为了反映泥质粉砂岩的非线性蠕变特性，基于上述特点，建立由修正的Burgers 模型和非线性黏塑性体串联而成的非线性黏弹塑性蠕变模型(NVEPB 蠕变模型)，见图3。图3中，σ为模型总应力；σK为开关元件的应力阀值；σs为理想塑性体的应力阀值；E1和E3分别为模型第1和第3部分的弹性参数；η2，η3，η4分别为模型第2，3，4 部分的黏性参数；n为蠕变指数。

图3 非线性黏弹塑性蠕变模型（NVEPB蠕变模型）Fig.3 Nonlinear viscoelastic-plastic creep model(NVEPB model)

NVEPB 蠕变模型中，定义了一个开关元件σK，该元件的物理意义是：当σ＜σK时，开关元件关闭，牛顿体不起作用，Burgers 模型转化为广义Kelvin 模型；当σ≥σK时，开关元件打开，牛顿体发挥作用，广义Kelvin 模型转化为Burgers 模型。开关元件与理想塑性体类似但本质上存在区别，开关元件的σK仅是蠕变门槛值，不分担荷载；理想塑性体的应力阀值σs表示达到临界塑性应变时的屈服应力，当应力水平超过σs时，它要始终分担大小为σs的应力。

岩石的加速流变是岩石内部微小裂缝不断萌生、扩展、贯通的结果，为此，将黏壶元件分解为线性部分和非线性部分，即岩石在进入加速蠕变阶段以前，黏滞系数η4为定值，岩石进入加速蠕变阶段后，η4急剧减小。直接将黏滞系数η4换成η4(σ,t)常常会得到错误的蠕变方程[21]。因此，将图3中非线性黏塑性元件的蠕变方程定义为

式中：Δt取单位时间，用来保持量纲一致；tF为加速蠕变启动时间[14]，即岩石从稳定蠕变阶段向加速蠕变阶段过渡的临界时间点；H(t-tF)为符号函数，

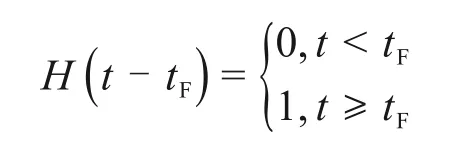
当t≺tF时，岩石为理想黏弹塑性体，可用来描述减速和等速蠕变阶段蠕变特性；当t≥tF时，岩石为非线性黏弹塑性体，可用来描述减速、等速和加速蠕变阶段蠕变特性。

2.2 NVEPB蠕变模型本构方程的推导

NVEPB蠕变模型中各部分满足：

式中：σ和ε分别为模型总应力和总应变；σi和εi分别为第i(i=1，2，3，4)部分的应力和应变；Ei和ηi分别为第i(i=1，2，3)部分的弹性模量和黏性参数；H(σ-σK)为符号函数，

根据式(2)可得七元件(NVEPB蠕变模型的蠕变本构方程如下。

1)当σ＜σK时，

2)当σK≤σ＜σs时，

3)当σ≥σs,t＜tF时，

4)当σ≥σs,t≥tF时，

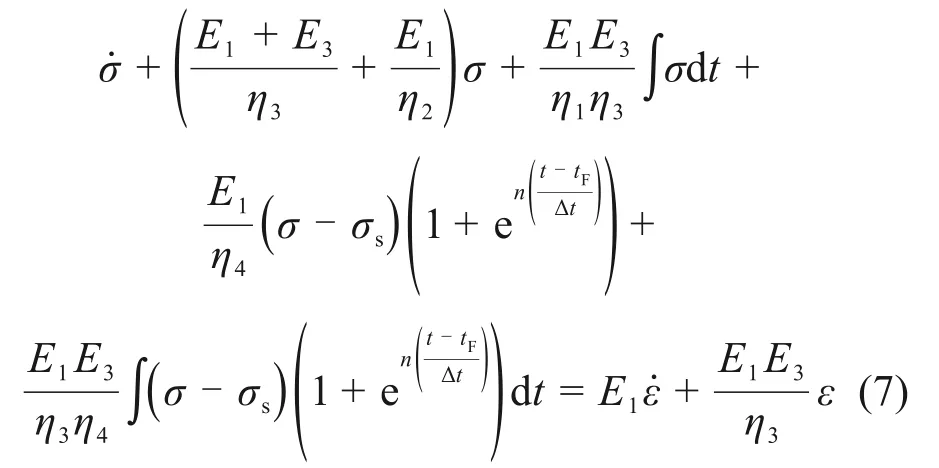
设在时间t=0 时刻施加一恒定不变应力σ=σ0＜σs，考虑初始条件ε2(0)=ε3(0)=ε4(0)=0，对式(2)作Laplace变换有

式中：为ε的拉氏变换，S为Laplace 变换中的复变量。对式(8)作Laplace逆变换可得

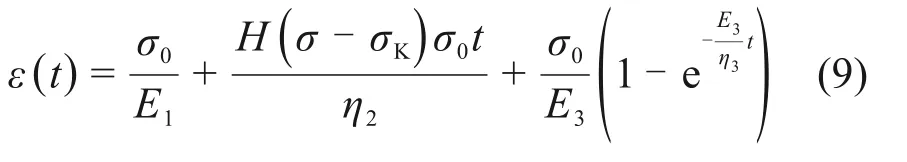
式(9)即为修正Burgers模型的蠕变方程。

设在时间t=0 时刻施加一恒定不变应力σ=σ0≥σs，并注意到初始条件ε2(0)=ε3(0)=ε4(0)=0。对式(2)作Laplace变换，可得

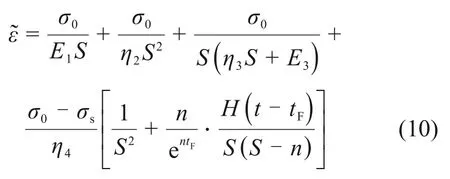
再对式(10)做Laplace逆变换，可得

于刚性轮，其中在空载工况中尤为明显，脱轨系数减小43.84%，超限时间减少26.09%。直线轨道上弹性轮和刚性轮的脱轨系数均未超过限值，弹性轮的最大值略小。

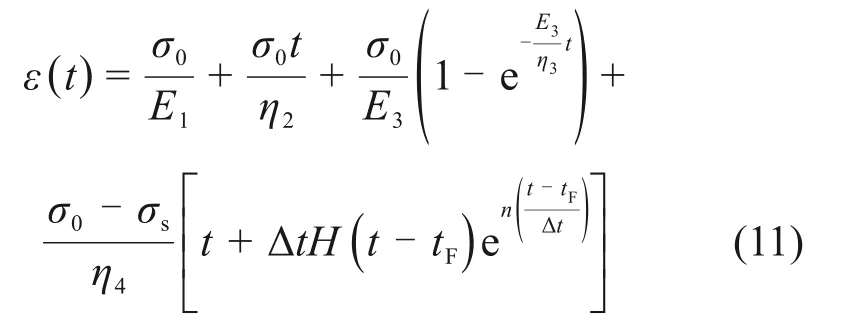
式(11)即为NVEPB 蠕变模型在破裂应力下的蠕变方程。

2.3 NVEPB蠕变模型蠕变方程的三维形式

地下岩体通常处于三维应力状态，推导三维应力状态下的NVEPB蠕变模型的本构关系对指导工程实践尤为必要。由图3及叠加原理可知，NVEPB 蠕变模型在三维应力条件下的总应变可以用张量表示：

式中：，，和分别为NVEPB蠕变模型第1～4部分的应变张量。

在三维应力状态下，材料内部的应力张量σij可以分解为应力球张量σm和应力偏张量Sij：

式中：δij为Kronecker函数。

根据塑性力学，满足材料各向同性的要求下，一般认为应力球张量不会引起岩石产生蠕变，只有应力偏张量会引起岩石产生蠕变。同理，材料内部的应变张量εij也可以分解为应变球张量εm和应变偏张量eij：

对三维应力状态下的NVEPB 蠕变模型第1 部分Hooke体，根据广义胡克定律可推导出：

其中：

K为体积模量；G为剪切模量；E为弹性模量；μ为泊松比。

对于三维应力状态下的黏弹性体的蠕变方程，可将单轴应力状态下的蠕变方程中的σ0用岩石试验时恒定偏应力(Sij)0替换得到[22]。由式(15)和(17)可以推导得到Hooke体的应变为

NVEPB 蠕变模型第2 部分修正Newton 体的应变为

NVEPB蠕变模型第3部分Kelvin体的应变为

对NVEPB蠕变模型第4部分非线性黏塑性体，由单向应力状态过渡到复杂应力状态，必须引入屈服面和塑性势的概念[22-23]。塑性体在三维应力状态黏塑性应变为

式中：F为岩石的屈服函数；F0为屈服函数的初始值，通常取F0=1；Q为塑性势函数；φ函数取幂函数形式，通常取幂指数为1[24]。

假设在常温或中低温条件下，不考虑应力球张量的影响，应力偏张量对岩石材料蠕变起主要作用，屈服函数F为

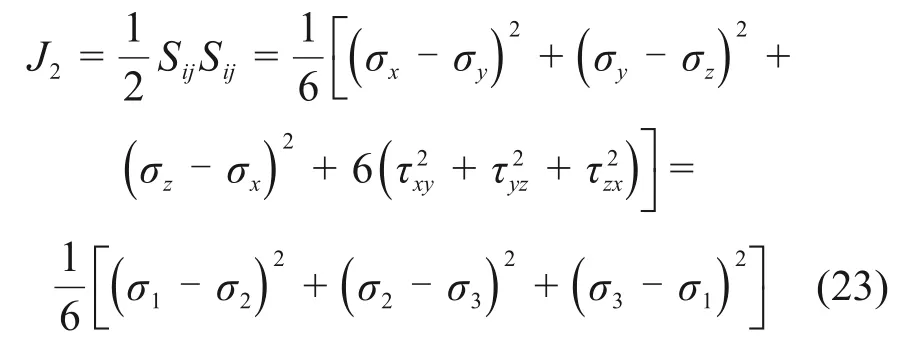
式中：J2为应力偏量的第二不变量。

假设岩石材料满足各向同性，在岩石蠕变过程中泊松比保持不变且岩石弹性应变和蠕变分别由应力球张量引起和应力偏张量引起等，结合前面各式，根据叠加原理，可以得到NVEPB蠕变模型在三维应力条件下的岩石蠕变方程：

式中：SS为三维应力状态下的长期强度。

在实验室常规三轴压缩应力状态下，有条件σ2=σ3(σ2和σ3为岩石试件所受围压)；取岩石轴向变形来描述岩石的蠕变全过程，即第一主应变ε11，则

结合式前面各式，可以得到常规三轴压缩应力状态下，NVEPB蠕变模型的蠕变方程为

式中：σs为岩石的长期强度，取倒数第二级应力水平[14]，即σs=49.82 MPa。近似认为应力水平超过这一阈值时，岩石将要发生加速蠕变破坏。

3 黏弹塑性模型的蠕变参数反演

为进行蠕变力学参数辨识，先对式(28)进行简化。由常规三轴试验可得围压20 MPa 下，岩石弹性模量为14 GPa，泊松比为0.3，K=11.7 GPa，由此可以确定NVEPB蠕变模型中Hooke体的应变。

借助Origin 平台，将NVEPB 蠕变模型在不同应力状态下的三维蠕变方程编程并嵌入其内置的非线性拟合模块，采用Origin 平台Levenberg-Marquardt 非线性最小二乘法对不同应力水平下泥质粉砂岩的蠕变试验曲线的蠕变参数进行反演。各级应力水平作用下岩石轴向蠕变试验曲线和NVEPB 蠕变模型拟合曲线的对比见图4。围压为20 MPa下泥质粉砂岩径向的蠕变参数见表2。

由图4和表2可知，NVEPB蠕变模型拟合得到的岩石轴蠕变理论曲线和试验所得蠕变试验数据高度吻合，拟合系数R2均大于0.94，充分证明提出的NVEPB蠕变模型的合理性与适用性。

表2 围压为20 MPa下NVEPB蠕变模型辨识的泥质粉砂岩蠕变力学参数Table 2 Creep mechanical parameters of argillaceous siltstone under confining pressure of 20 MPa identified by NVEPB model

图4 NVEPB蠕变模型计算曲线和试验曲线的比较Fig.4 Comparison between calculation curves of NVEPB model and test curves

4 非线性黏塑性体蠕变指数对蠕变曲线的影响

加速蠕变段的应变记为εacce(t)：

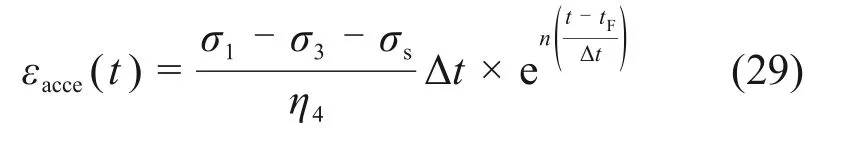
式中：取σ1-σ3-σs=10 MPa，η4=1 000 GPa·h，0≤t-tF≤5 h；n=0.5，0.6，0.7，0.8，0.9，1.0，2.0。εacce(t)与n的关系如图5所示。

由图5可见：随着非线性黏塑性体蠕变指数n增大，加速蠕变段的应变εacce(t)的增长速度越来越快，尤其是当n从1 增加到2 时，非线性黏塑性体的应变增大约200倍。由此可见非线性黏塑性体可以描述岩石在加速蠕变阶段应变随时间剧烈、快速变化的性质，充分反映了建立的非线性黏塑性体对于岩石非线性加速蠕变特性描述的优越性。

图5 非线性黏塑性体蠕变指数n对蠕变曲线的影响Fig.5 Influence of creep index n on creep curves of nonlinear viscoplastic body

5 结论

1)本室内三轴蠕变试验揭示了滇中引水工程香炉山隧洞深度1 km处T3sn泥质粉砂岩存在门槛效应，当应力水平低于蠕变门槛值时，流变效应不太显著，仅存在减速蠕变阶段，减速蠕变阶段的蠕变速率趋近于0；当应力水平高于蠕变门槛值时，蠕变效应逐渐显现，开始出现等速蠕变阶段，蠕变速率趋近于恒定正值，且蠕变速率随应力水平提高而增大。

2)根据泥质粉砂岩的蠕变曲线特征，引入了开关元件与牛顿体并联形成修正Newton 体，修正Newton 体与Hoek 体、Kelvin 体串联形成修正Burgers模型，修正Burgers模型与提出的非线性黏塑性体串联形成非线性黏塑性蠕变组合模型(NVEPB 蠕变模型)，它可以更精确地描述岩石蠕变的减速、等速尤其是加速蠕变阶段的应变随时间的变化规律。

3)推导了三轴应力状态下的八元件NVEPB蠕变模型的三维本构方程，并对模型进行参数辨识，蠕变试验曲线与模型理论曲线十分吻合，拟合系数均大于0.94，充分证明了该蠕变组合模型的合理性与适用性。

4)NVEPB 蠕变模型中，非线性黏塑性体的非线性随蠕变指数的增大而不断提高，在岩石加速蠕变阶段应变快速剧烈变化的情况下，其优越性更加明显。

5)所建立的NVEPB蠕变模型可描述更多软岩的蠕变力学性质，具有较大的工程应用价值。