基于随钻电阻率成像测井仪的洞穴评价模型理论研究

2021-06-21康正明柯式镇李新倪卫宁李飞

中南大学学报（自然科学版） 2021年5期

康正明，柯式镇，李新，倪卫宁，李飞

(1.西安石油大学陕西省油气井测控技术重点实验室，陕西西安，710065；2.西安石油大学电子工程学院，陕西西安，710065；3.中国石油大学(北京)地球物理学院，北京，102249；4.中国石化石油工程技术研究院，北京，100101)

随钻电阻率成像测井是地球物理勘探中一种精细化描述井筒附近地质构造的方法，据高精度的采样率得到的井壁图像不仅可以直观展示其附近缝洞体，而且可以进行储层参数计算，因此，该技术在钻完井中优势明显，可以准确监测井下地质环境，为低渗透油气藏高效开发提供了丰富的地层信息，是实现优快钻井和提高开发效益的基础[1-3]。随着井下数据传输技术和小纽扣电极技术的不断进步，最新的测量仪器分辨率与地层微电阻率成像仪(FMI)的分辨率相当[4-5]。

洞穴是油气储层中常见的地质构造，不仅可以作为油气的运移通道，而且可以进行油气储集。洞穴的发育往往具有强非均质性与各向异性，因此，测井响应复杂，测井识别与定量评价难度较大[6]，利用电阻率成像测井图像，可以较快地发现洞穴的存在。在洞穴参数计算方面，理论上通过井场实时反演可以定量评价，但含有洞穴的三维地层模型较大，反演耗时耗力，在实际应用中难以实施。相比而言，三维正演在其参数计算模型建立中发挥重要作用，可有效提高反演速度和精度。通过对特定模型进行正演模拟，确定洞穴参数与测量信号的定量关系，从而可以获得洞穴参数解释模型。关于洞穴地层的测井响应研究，前人做了大量模拟工作，但是大多数都聚焦在双侧向测井仪器和电磁波传播测井仪器方面[7-13]，而对于随钻电阻率成像测井仪器在洞穴地层的测井响应机理的研究很少，目前主要的数值模拟集中在仪器的探测特性、常见典型地层测井响应特征、环境影响因素等方面[14-19]，采用的模型主要基于水平层状地层和倾斜层状地层[10]。因此，很有必要利用数值模拟手段研究其在复杂洞穴地层的测井响应机理并建立其参数解释模型。

在仪器探测深度方面，双侧向测井对洞穴直径大于1 m 以上的洞穴具有较好的识别和评价效果，而成像测井对小于这一尺寸的洞穴可以显示出洞穴图像。不同于一般测井仪器的数值模拟模型，随钻电阻率成像测井响应的模型尺寸变化较大，比如几厘米的纽扣电极、长达几米的测井仪器和地层，因此，属于多尺度问题[20]，目前，大多采用有限元素法模拟。本文针对直径1 m以下的洞穴，基于三维有限元建立单洞穴和多洞穴模型，考察随钻电阻率成像测井的响应特性，通过分析洞穴参数与测量信号的定量关系，建立洞穴直径和洞穴延伸度计算模型，以便为随钻电阻率成像测井在复杂地层测井响应机理和解释模型提供理论支撑。

1 三维有限元建模

1.1 基本原理

随钻电阻率成像测井仪器有2种激励机制，其中，一种是直接给电极加载电流，另一种是通过螺绕环激励在钻铤上产生等量电位以达到自动聚焦的作用。第二种方法在工艺上容易实现，因此被广泛应用[18,21]。在不考虑测量频率的影响的情况下，可以将激励源螺绕环等效为延伸的电压偶极子，其在地层中产生的电场与在侧向测井中产生的电场类似，满足拉普拉斯方程，对电流面密度的拉普拉斯方程进行求解可获得。在直角坐标系下，地层电阻率为R时电流密度J(x,y,z)满足以下泛函表达式[22]：

式中：F(J)为J(x,y,z)的泛函；Ω为求解区域；UC为钻铤表面电压；IC为下接收螺绕环接收到的轴向电流。

钻铤表面电压UC和无限远地层边界电压UI满足第1类边界条件[16]：

式中，C为常数。

根据边界条件和电阻率分布满足条件，过对F(J)进行离散化，可得到每个单元的表达形式：

将求解的所有单元的节点合起来形成要求解的刚度矩阵：

式中，K为总刚度矩阵：J为电流密度矩阵；S为施加条件矩阵。

式(4)为大型稀疏矩阵，采用广义最小余量法(FGMRES)对式(4)求解，即可得到纽扣电极处的电流密度J，然后对电流密度J进行面积分，即可获得纽扣电极处的电流I：

最后，利用欧姆定律即可获得地层视电阻率Ra。

1.2 模型

洞穴地层一般不对称，因此，需要借助三维模型进行模拟。对复杂仪器结构进行简化可减小计算量，因此，本文在数值模拟中忽略了螺绕环线圈结构，将之等效为延伸的电压偶极子。同时，将钻铤结构掏空，只对其面赋予相关物质属性。分别设计了单洞穴和多洞穴2种地层模型模拟洞穴地层测井响应，其中，单洞穴模型用于模拟测量点与洞穴中心处于同一深度时的测量信号，多洞穴模型用于成像采样过程模拟，得到的洞穴成像结果可以更加直观地反映不同因素对洞穴的影响。

图1所示为单洞穴地层模型截面示意图，模型由随钻电阻率成像测井仪器、井眼、基岩和洞穴组成。钻铤直径为17.02 cm，包括1 个发射螺绕环、2 组纽扣电极和2 个接收螺绕环。2 组用于成像的纽扣电极B1 和B2 纵向分布，其直径分别为10 mm和25 mm，每组纽扣在周向上间隔90°分布。纽扣电极B1的4个电极分布于正北、正东、正南、正西方向，标记为1，3，5，7，类似地，纽扣电极B2 的4 个电极分别标记为2，4，6，8。模拟中采用的仪器参数具有普遍性，因此，得到的洞穴参数解释模型具有一定的通用性。

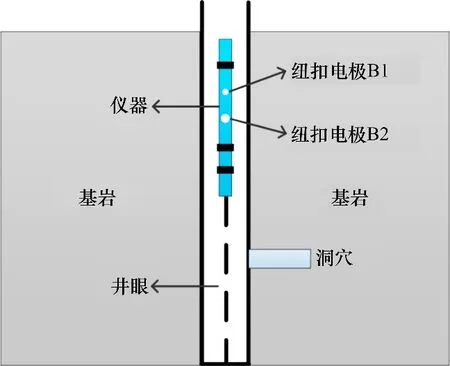
图1 单洞穴模型示意图Fig.1 Schematic of single cave model

在单洞穴模型中，分别将1号和2号纽扣电极正对洞穴进行模拟用于考察不同纽扣电极直径对洞穴测井响应的差异。洞穴形状采用柱状、过井眼型洞穴。

单洞穴模型中，主要分析洞穴直径、洞穴电阻率、洞穴延伸长度对测量信号的影响。根据地质上洞穴尺寸的分类方法，将洞穴分为中等洞穴(直径为10 mm)和大洞穴(直径为50 mm)。表1所示为单洞穴测量信号影响因素模拟参数，洞穴位于正北方位。

表1 单洞穴模拟参数Table 1 Simulation parameters of single cave

多洞穴模型俯视图如图2所示，6 个洞穴分布在正北、东北、正东、东南、正南、正西方位，每个洞穴中心在纵向上处于同一深度。考察洞穴直径、洞穴电阻率、洞穴延伸长度不同时，洞穴图像的差异。表2所示为多洞穴测量信号影响因素模拟参数，当考察因素的参数有多个时，参数依次与洞穴1～6相对应。

表2 多洞穴模型模拟参数Table 2 Simulation parameters of multi cave model

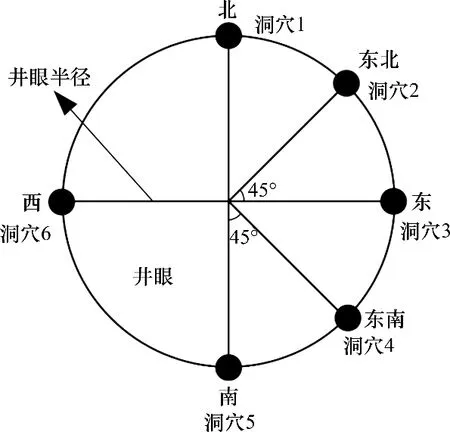
图2 多洞穴模型俯视图Fig.2 Top view of multi caves model

1.3 网格剖分

模拟过程中，需要对模型进行区域分解，针对不同区域设置不同的网格尺寸，而且需要控制不同区域网格的彼此影响，以达到求解精度和提高求解速度。本文采用有限元局部网格细化技术以解决网格自由度过大或者计算精度不足的问题。网格细化区域包括纽扣电极表面、洞穴、井眼等部分。其中，钻铤、井眼、纽扣电极等表面，采用三角形网格进行加密，由于是面网格，因此，这部分网格数量较少，但能较大地提升电流采集的精度。除了对研究对象本身进行加密外，模型还增加了1个全新的柱状体域，将洞穴全部包含在内，并对该域进行网格加密。为了与上述表面三角形网格更好地匹配，洞穴和地层等区域的网格剖分采用四面体网格。

2 数值模拟结果分析

2.1 洞穴直径

模拟洞穴形状为圆柱体，与井轴正交且被井眼钻穿。洞穴直径小于井眼直径，因而，二者在井壁上形成的交线不规则，在机械行业称之为二者的“相贯线”。当二者直径相差较大时，相贯线类似于圆，如图3所示。

图3 洞穴与井眼相贯线示意图Fig.3 Intersecting line schematic between cave and borehole

在地质上，将直径在2 mm以上的孔隙称为洞穴，其中，直径为2～5 mm 的为小洞，直径为5～10 mm的为中洞，直径大于10 mm的为大洞[23]。本文研究的洞穴直径为10～100 mm，洞穴与井眼正交的相贯线接近圆，方便图像分析。洞穴直径对测量信号的影响如图4所示，其中，Imax为纽扣电极中心和洞穴中心在同一纵向位置时纽扣电极测量电流，Imin为纽扣电极正对基岩时测量电流。当背景地层电阻率不变时，Imin几乎不变，电阻率成像测井数据成像后反映的是电流对比度的变化，因此，采用Imax/Imin表征不同因素变化对测量信号的影响。

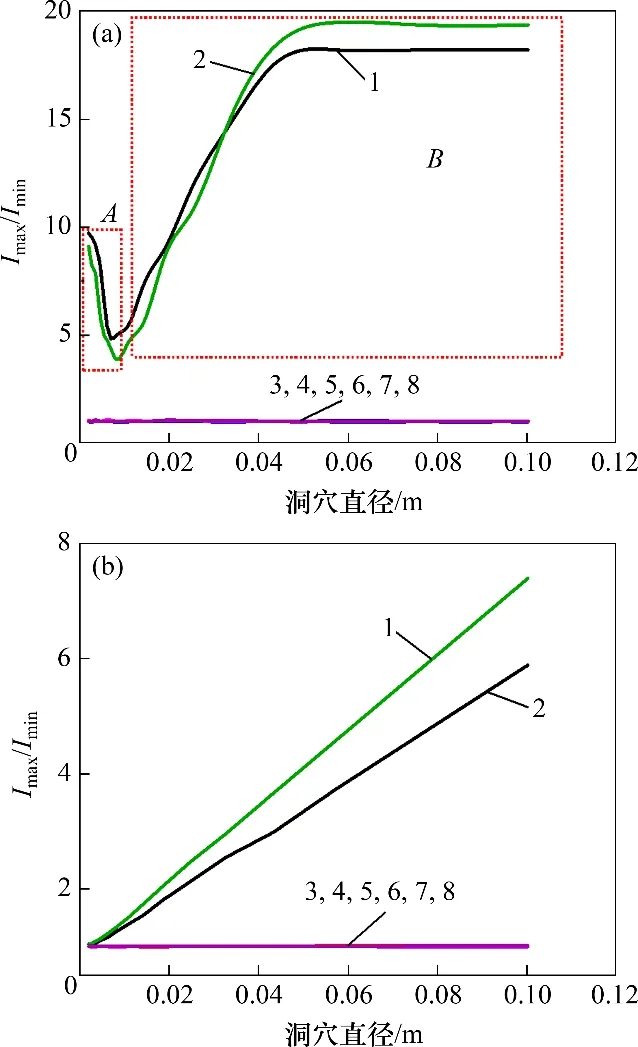
图4 洞穴直径对测量信号的影响Fig.4 Effect of cave diameters on measured signals

从图4(a)可以看出，当存在井眼时，正对洞穴的纽扣电极测量信号影响较大。当洞穴直径小于100 mm时(区域A)，测量信号较大，随着直径的增大，测量信号逐渐变小，此时，测量的信号几乎来自于井眼，受井眼的影响，该方位纽扣电极无法较好地识别洞穴；当洞穴直径大于100 mm时(区域B)，随着洞穴半径的增大，测量信号增大至趋于平稳。从图4(b)可以看出，不考虑井眼时，随着洞穴直径从2 mm 变化到100 mm，正对洞穴的纽扣电极测量信号逐渐增大，呈线性关系，而其他方位纽扣电极信号对洞穴不敏感，几乎无法检测到洞穴的存在。因此，有效消除井眼的影响成为准确地识别洞穴的关键所在，目前常用的方法是将纽扣电极紧贴井壁进行测量。

根据模型参数(表2)，固定仪器钻铤直径为17.02 cm，井眼直径分别为17.78 cm 和21.59 cm，即纽扣几乎贴在井壁和纽扣距离井壁较远的情况，模拟分析井眼对不同直径洞穴的影响。图5和图6所示分别为21.59 cm 和17.78 cm 井眼环境下不同直径洞穴的成像结果，方位依次为北、东、南、西、北(下同)。可见，当洞穴直径小于10 mm 时，大小纽扣电极均无法识别出洞穴的存在，当洞穴直径大于等于10 mm 时，大小纽扣电极均可以识别洞穴。洞穴直径越大，成像效果越明显，越能够清楚地、完整地显示出洞穴的实际形状。对比图5和图6可知，当纽扣越靠近井壁，洞穴成像分辨率越高。因此，在考察洞穴延伸度和洞穴电阻率参数对测量信号影响时，控制井眼直径为17.78 cm。

图5 直径21.59 cm井眼中不同直径洞穴成像结果Fig.5 Imaging results of caves with different diameters in borehole with diameter of 21.59 cm

图6 直径17.78 cm井眼中不同直径洞穴成像结果Fig.6 Imaging results of caves with different diameters in borehole with diameter of 17.78 cm

2.2 洞穴电阻率

选取泥浆为填充物，与实际随钻测井情形相符，其电阻率Rm从0.2 Ω·m 到20 Ω·m 变化，背景地层电阻率Rb固定为100 Ω·m。图7所示为单洞穴模型下正对洞穴方向纽扣电极测井响应特征。从图7可以看出，在双对数坐标系下，随着Rm/Rb增大，大小纽扣电极在中洞穴和大洞穴中测量的电流对比度呈线性递减趋势(实际为幂指数关系)。

图7 洞穴填充物电阻率对测量信号的影响Fig.7 Effect of cave filter on measured signals

设置洞穴的直径和延伸长度为定值，模拟不同洞穴填充物的成像结果如图8所示。从图8可见：当洞穴填充物电阻率比基岩的高时，洞穴图像为亮色，接近白色；当洞穴填充物电阻率与基岩电阻率相等时，洞穴图像和基岩颜色一致，此时无法判断出洞穴的存在；当Rm/Rb为0.1时，可以从成像结果看出洞穴的存在，但是对比不明显；当Rm/Rb为0.01 时，此时可以清晰识别出洞穴的存在。

图8 不同填充物时洞穴成像结果Fig.8 Imaging results of caves with different filters

2.3 洞穴延伸长度

电缆式微电阻率成像测井图像可以直观地显示洞穴的分布特征，但其探测范围有限，仅能提供井壁的洞穴信息，很难反映洞穴的径向发育特征；双侧向测井探测深度较深，但是其对于直径小于1 m的洞穴不敏感。与这2种仪器相比，随钻电阻率成像测井的探测深度较电缆式仪器的探测深度大且对直径较小的洞穴具有较好的识别功能。

图9所示为延伸长度对不同纽扣电极的测量信号的影响。从图9可以看出：对于中洞穴，随着延伸长度从100 mm增加到500 mm，B1和B2电极正东、正南、正西信号几乎没有变化，Imax/Imin接近1，说明洞穴对测量信号几乎没有影响；当洞穴延伸长度小于150 mm时，正北方位的纽扣电极测量信号与洞穴延伸长度具有非线性变化关系，且Imax/Imin远大于1，考虑到洞穴直径较小，因此，这主要是受井眼泥浆的影响；当洞穴延伸长度大于150 mm时，大小纽扣电极测量的电流信号不随洞穴延伸长度的变化而变化，说明此时井眼对测量结果的影响趋于稳定；对于大洞穴，随着洞穴延伸长度的增大，洞穴正对的纽扣电极测量信号呈现幂指数变化。

图9 洞穴延伸长度对测量信号的影响Fig.9 Effect of cave extension on measured signals

图10所示为不同延伸长度时洞穴的成像结果。从图10可以看出：当洞穴延伸长度小于20 mm时，很难通过图像识别洞穴；当洞穴延伸长度为50～100 mm 时，能够识别洞穴的存在，但是图像无法还原洞穴的形状，而当洞穴延伸长度达到150 mm时，不但能够识别洞穴的存在，而且可以通过图像大致判断洞穴的形状。

图10 不同延伸长度洞穴成像结果Fig.10 Imaging results of caves with different extensions

3 洞穴参数计算模型

3.1 洞穴直径计算模型

通过对随钻电阻率成像测井资料进行处理，可以计算出洞穴的面孔率、洞穴直径以及洞穴密度，本文主要针对不同洞穴直径计算模型得到的成像结果进行分析。通常利用电流异常面积计算洞穴直径，即从图像出发，利用电成像测井的静态图，按照灰度差将洞穴从骨架背景中提取出来，然后根据其直方图得到分割阀值T，利用下式可计算出洞穴的面积A：

式中：H(D)为灰度直方图；D为洞穴直径。

由于式(6)在求取洞穴处电流异常面积积分时往往误差较大，因此，需要对模型进行改进。由上述模拟结果可知，洞穴处最大电流对比度Imax/Imin与洞穴直径D为线性关系，Imax/Imin与Rm/Rb呈幂指数关系，对上述关系进行拟合，分别得到

式中：a，b，c，d均为常数。

令y=Imax/Imin，式(7)和式(8)可变为：

Rm/Rb固定时，

Rm/Rb不固定时，则有

式中，Q为常数。

通过式(11)和(12)可得到在任何Rm/Rb下的洞穴直径D定量评价公式：

利用上述理论模型，对图6(b)中纽扣电极B1的模拟图像中的4个洞穴进行直径计算，结果如表3所示。从表3可以看出，利用模型计算得到的洞穴直径更加接近真实值，当洞穴直径大于25 mm时，计算得到的相对误差小于3.2%，洞穴直径越大，模型得到的相对误差越小。新模型计算得到的洞穴直径结果表明，利用电流对比度评价洞穴直径模型效果较好。

表3 洞穴直径计算结果Table 3 Calculation results of cave diameter

3.2 洞穴延伸长度计算模型

由图9(b)可知，洞穴延伸长度Ex和测量信号Imax/Imin具有幂指数关系。对洞穴延伸长度Ex和纽扣电极B1和B2的测量信号Imax/Imin进行拟合。拟合公式如下：

对拟合公式进行简单的变换，即可得到大洞穴延伸度的理论计算模型。表4所示为Imax/Imin模拟结果和计算结果的相对误差。从表4可以看出：Imax/Imin相对误差大多在5%以内，说明通过随钻电阻率成像测井获得正对洞穴方位的Imax/Imin，再应用上述公式可以求取大洞穴的径向延伸长度。通过理论计算可以得到不同洞穴直径对应的延伸长度计算公式系数。此外，不同直径洞穴延伸长度和测量信号关系的大量模拟也论证了上述结论。值得注意的是，只有大洞穴直径为100～500 mm 时，通过此模型计算得到的洞穴延伸长度才更加准确。同时，洞穴延伸长度模型适用条件为围岩电阻率和洞穴电阻率对比度较大的情况(Rm/Rb＞10)，特别适用于低阻的水基泥浆侵入洞穴、围岩电阻率为高阻的情况。