动点轨迹中的“定”元素

黄晓南

【摘要】动点轨迹问题一直是近年来广东中考的一个热 点、难点问题，学生在解决此类问题时，需要明确运动的轨迹，而关键的突破口在于运动过程中“定”的元素。教师要引导学生抓住图形的几何特征，才能从本质上发现运动的根本轨迹。“隐形圆”是广东中考新出现的动点轨迹考点，本文将从利用“隐形圆”求解线段最小值的角度出发，分析解 决此类问题的基本思想方法。

【关键词】隐形圆;动点;轨迹;最小值

一、问题背景

各地中考中，求线段的最值问题是时常出现的考题。基本可分为两类：一类是只求一条线段的最值问题;另一类是由两条或多条线段的和或差形成的最值问题。2020 年广东中考题填空题第 17 题——“猫捉老鼠”模型，就是利用“隐形圆”求解一条线段最小值问题的一个典型例子。笔者将从这个问题开始讲起，分析解决此类问题的基本做法。

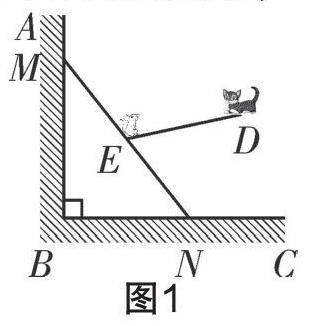
例 1：（2020 年广东中考）有一架竖直靠在直角墙面的梯子正在下滑，一只猫紧紧盯住位于梯子正中间的老鼠，等待与老鼠距离最小时扑捉。把墙面、梯子、猫和老鼠都理想化为同一平面内的线或点，模型如图 1，∠ABC=90°，点 M、N 分别在射线 BA、BC 上，MN 长度始终保持不变，MN=4， 点 E 为MN 的中点，点 D 到 BA、BC 的距离分别为 4 和 2。在此滑动过程中，猫与老鼠的距离DE 的最小值为              。

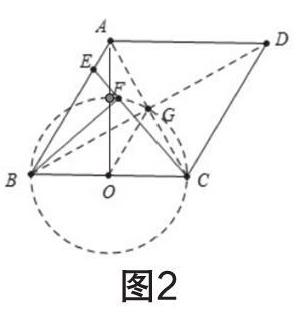
分析：本题考查的知识点主要有直角三角形斜边上的中线性质;勾股定理的应用;两点之间线段最短等。题目中由于 MN 的运动，导致了点 E 发生运动，而整个运动过程中，MN 保持不变，∠ABC=90°，且点 E 为 MN 的中点，故 BE 也是不变，此为运动中的“定元素，并且 BE=    MN= 2，（直角三角图形斜边上的中线等于斜边的一半）;因此不难发现点 E 的运动轨迹落在半径为 2 的⊙B 上（如图 2）， 那么 DE 的最小值即为点D 到⊙B 的最短距离，此时D、E、B 三点共线，根据勾股定理可求出 BD=2  5 ，所以 DE 最小值为 2  5 -2。

本题看似计算结果简单，实则有一定的难度。学生容易利用勾股定理计算，同时也会知道“两点之间线段最短”， 但关键点在于发现点E 的运动轨迹，找出“隐形圆”，从而把“线段最值问题”转化为“圆外一点到圆上的点距离最近问题”。这种考查就特别要注意学生平时课堂活动经验的积累，并对“数形结合”及“数学转化”思想的进行有效培养。

二、问题基本模型

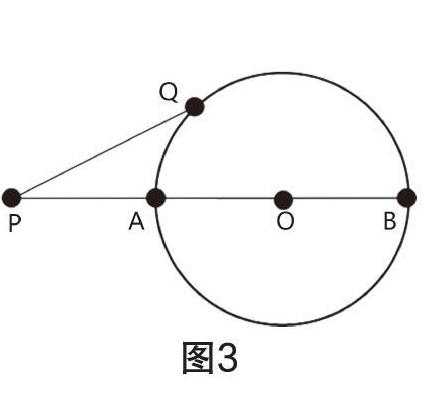
利用“隐形圆”求线段最值问题，要清楚了解问题的基本模型，如图 3，当点 P 为⊙O外一点，直线PO 与⊙O分别交于A、B 两点，那么，根据“三角形任意两边之和大于第三边;任意两边之差小于第三边”，点 P 到圆上任意一点 Q 的最小距离则是线段 PA 的长;点 P 到圆上任意一点 Q 的最大距离是线段 PB 的长。明确问题基本模型，我们便可以将“两点间线段的长度最值” 的问题转化为“定点 P 到圆上一点的距离最值”的问题。通过探索动点运动轨迹是隐形圆或弧，利用“隐形圆”与直线的两个交点的关系，即图 3 中的 PA 为最短距离，PB 为最长距离来求线段长的最小值或最大值。

三、典型例题分析

为了更好地运用以上基本模型，下面将选用两个经典例题，分析如何在运动上找出“定”元素构造“隐形圆”，然 后将线段最值问题转化为定点到圆上一点的距离最值问题。

例 2：（2020 年揭西县中考模拟改编）如图 4，在菱形ABCD 中，∠ABC=60°，AB=6，点 E 是 AB 边上的动点，过点B 作直线CE 的垂线，垂足为 F，连接 AF，当点 E 从点 A 运动到点 B 时，线段 AF 的最小值为（        ）

A.3    B.6    C.3  3  -3      D.6  3 -6

分析：首先，点 E 的运动导致了点F 的位置变化，而在整个变化过程中，∠BFC=90°，BC 不变，这是“定”的元素。可判断点 F 在以 BC 为直径的圆上运动（如图 5）。由于点 E 只在 AB 间运动，因此，连接 AC、BD 交于点 G，故可判断点 F 的运动轨迹是在 BG上;其次，假设 BG所在圆心为 O，连接 AO，此时将AF 的最短距离转化为点A 到⊙O的最短距离;最后，利用锐角三角函数或勾股定理求得 AO=3 3 ，所以 AF 最小值为3 3  -3。故选择 C。

本题目利用菱形的性质作为背景，考查了学生对动点运动轨迹的观察与判断，关键突破口在于发现直角所对的弦为直径，利用直角这一“定”元素找出“隐形圆”，最后运用 数学转化将 AF 的最短距离转为定点 A 到⊙O的最短距离进行解决。

例 3：如图 6，△ABC 是等边三角形，AB=2若 P 为△ABC 内一动点，且满足∠PAB=∠ACP则线段PB 长度的最小值是           .

分析：本题目条件比较简单，需要学生观察发现点P 的运动轨迹，整个问题中∠PAB=∠ACP 是分析解决问题的关键。因为∠PAB=∠ACP，∠PAB+∠CAP=60°，所以∠APC=120°; 结合等边三角形的性质，不难发现AC=6，∠APC 在整个运动过程中保持 120°不变，这就是本题中的“定” 元素。故点 P 落在 A、C、P 三点确定的圆上，则找出了“隐形圆”。

由于点 P 在 AC上运动，不难发现当点 P 位于 AC中点时，PB 取得最小值，此时 B、P、O 三点共线，连接 BO，交AC 于点 G，利用垂径定理可知∠CGP=90°，∠CPG=60°，故可利用锐角三角函数求得 BG= 3 ，PG=     ，所以 PB 的最小值为       。

本题目要求学生能够综合考虑等边三角形的基本性质， 准确判断 A、P、C 三点共圆的由来，在与学生交流时，发现大多学生容易把思路偏向于利用相似三角形来解决，这是由于对∠PAB=∠ACP 这一条件的作用没能准确把握的缘故。在找出“隐形圆”后，运用垂径定理及锐角三角函数进行求解， 也是大多数学生的一个难点所在。

四、总结思考感悟

综合以上问题的探究与分析，我们发现基础知识是学生解决数学问题的最基本要素。按新课程标准的要求，中考应注重考察基础知识、基本技能;注重考察思维过程、创新意识和分析问题、解决问题的能力。这便要求教师在教学过程中，应注重引导学生进行学习活动经验的积累，要注重数学学习方法的归纳与总结，并提炼成一种常用的技巧和方法， 这不仅有利于拓宽学生的解题思路、提高学生分析解决问题的能力，同时也对培养学生形成良好学习习惯、优化思维创新意识具有重大意义。

在“隐形圆”的问题教学中，教师要善于引导学生发现动点题目中不变的量，不变的性质和不变关系，以“定”的元素来确定“動”的轨迹，对题目的基本数学模型进行分析。 在提炼出问题的基本模型后，还应当注意对数学问题的转化，将要求的线段最值问题，转化为最基本的定点到圆上一点距离的最值问题，达到解决问题的最终目的。

【参考文献】

[1]张洁彬.巧用隐形圆解决线段的最值问题[J].中国校外教育（上旬刊），2019（3）：67-68.

[2]何君青.利用“隐圆” 巧解“线段最值题”[J].中学数学（初中版），2017（12）：84-85.