理论最低潮面确定方法探讨
2021-06-20卓玉生
卓玉生,王 岩
(中交第一航务工程勘察设计院有限公司,天津 300220)
引言
我国对理论最低潮面的计算方法的规定有一个发展过程,而通常情况下,理论最低潮面一旦确定,不宜轻易变动,这就导致国内理论最低潮面采用值复杂多样。同时,相同计算方法下,计算时采用不同的数据长度、年份,也可能得到不同的结果,给港口与航道工程及航运带来较多困扰。在此,对确定理论最低潮面的计算方法进行总结,并对其影响因素进行汇总分析,为确定理论最低潮面给出方法和建议。
1 理论最低潮面及相关概念
理论最低潮面,是根据前苏联弗拉基米尔斯基提出的方法[1]计算出的平均海面以下理论上能达到的最低潮位,通常记为平均海面到理论最低潮面的距离。理论最低潮面是国际上常用的深度基准面之一,也是常用的潮高基准面之一。深度基准面是水深测量工作中水深的起算面,现行国家标准《海道测量规范》(GB12327-1998)明确规定“以理论最低潮面作为深度基准面”[2]1,其算法为弗拉基米尔斯基方法的改进算法。现行国家标准《中国海图图式》(GB12319-1998)也做出规定:“中国沿海地区一般采用‘理论最低潮面’作为深度基准”[3]。根据国家海洋信息中心编制的潮汐表[4]说明中描述,“潮高基准面与海图深度基准面一致”。
港口与航道工程及航运中,确定适宜的理论最低潮面数值是一项重要的基础性工作。确定深度基准面时,既要考虑船舶的航行安全,又要考虑航道的利用率,这是确定海图深度基准面时的基本原则。深度基准面定得过高,船舶容易发生事故;深度基准面定得过低,则降低了航道的利用率。
2 理论最低潮面计算原理
理论最低潮面概念是前苏联弗拉基米尔斯基提出的,其计算原理概括为:利用潮位调和常数,选取振幅较大的13 个分潮,通过一些规定和算法,求取平均海面下能达到的最低潮位。其算法中的13 个分潮包括三部分:M2、S2、N2、K2、K1、O1、P1、Q1等8 个主要分潮,M4、MS4、M6等3 个浅水分潮和Sa、Ssa等2 个长周期分潮。为方便进行算法对比分析,以下内容对算法中间过程进行了提炼和概化,详细过程可参见文献[1]或文献[5]。
1)8 个主要分潮部分
8个主要分潮在平均海面上t时的潮高h8(t)可表示为:
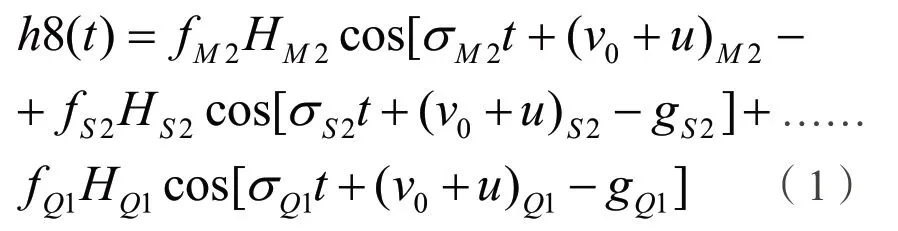
式中f、H、g、σ分别为各分潮的交点因子、振幅、迟角、角速度,v0+u为各分潮在格林威治1 月1 日0 时的相角,t为平太阳时。
通过形式变换(1)式可变换为以下形式:

式中φ为各分潮的相角,均可用以φK1为变量的函数表示,R、ε为辅助变量,其中R始终为正值。当φM2-ε1=180°、φS2-ε2=180°φN2-ε3=180°时,cos180°=-1,h8(φK1)可能为极小值,用L8(φK1)表示,即
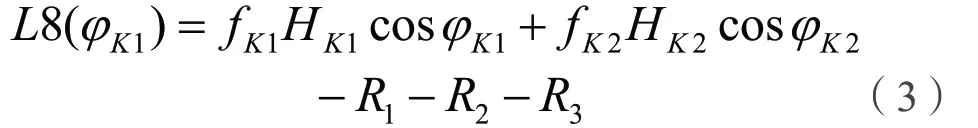
φK1从0°到360°变化,选取L8(φK1)的最小值,即为8 个主要分潮组合出的最低潮位,记为L8,对应的φK1相角记为(φK1)8min。
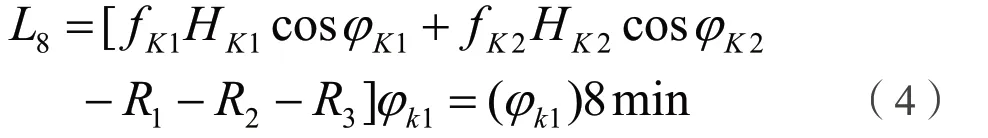
2)3 个浅水分潮改正部分
3 个浅水分潮在平均海面上t时的潮高改正可表示为以φK1为变量的函数:

式中φ为各分潮的相角,均可用以φK1为变量的函数表示。
根据L8对应的相角(φK1)8min,求出3 个浅水分潮的相角φ,计算各分潮的fHcosφ值,最后求其总和,记为ΔL3。

3)2 个长周期分潮改正部分
对于平均海面季节变化较大的海区,可根据由一年以上潮位资料分析所得潮汐调和常数的长周期分潮Sa和Ssa来进行改正。
2 个长周期分潮在平均海面上t 时的潮高改正可表示为以φK1为变量的函数,记为

式中φ为各分潮的相角,均可用以φK1为变量的函数表示。
根据L8对应的相角(φK1)8min在其±60°范围内以15°间隔为样本,分别通过查表(或通过公式)求取ε2等相关辅助角[1],进而分别求出2 个长周期分潮的相角,计算2 个长周期分潮的贡献之和,选取最小值,记为ΔL2。

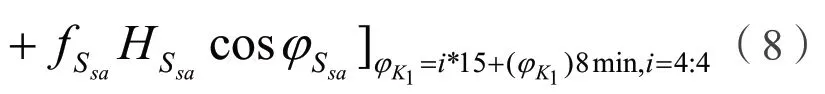
该项改正也可采用海平面季节改正数。
以上三部分,L8部分算法较稳定;ΔL3部分在3 个浅水分潮振幅之和在20 cm 附近时,由于其算法的不连续性,浅水分潮调和常数的较小变化,可能出现理论最低潮面的较大变化;ΔL2部分对“平均海面季节变化较大”没有量化的判别,对其理解容易产生分歧,从而导致不同人使用相同潮位数据计算理论最低潮面结果不唯一。
3 确定理论最低潮面的影响因素
3.1 理论最低潮面算法演变
通常深度基准面一旦被正式采用,不宜轻易改变。现行国家标准《海道测量规范》(GB 12327-1998)明确规定[2]:“深度基准面一经确定且在正规水深测量中已被采用者,一般不得变动”。该规定弱化了现行规范算法的强制执行要求,基于此点,很多港口或海域采用的理论最低潮面数值并未因规范规定算法的变化而改变,从而加剧了我国沿海采用的深度基准面的复杂多样。在此,列出我国理论最低潮面算法的主要演变过程,并对比各算法的特点和相互之间的差异。由于对理论最低潮面的理解有分歧,诸多文献发布了不同的改进算法[6-8],在此不作描述。
1956 年以前,我国采用的深度基准面不统一,主要采用略最低低潮面作为深度基准面,也有采用实测最低潮位、实测中等水位、平均海面等其他潮面的。
1956 年以后,海军司令部海道测量部在全国海洋测绘中,统一采用理论最低潮面(初期称“理论深度基准面”),其算法主要依据前苏联弗拉基米尔斯基方法(以下简称“弗拉基方法”)。1959 年海军司令部海道测量部出版的《实用潮汐学》是早期重要的参考文献。
1975 年,《海道测量规范》-水深测量(以下简称“75 规范”)规定:“长、短期验潮站的深度基准面,根据八个分潮(M2、S2、N2、K2、K1、O1、P1、Q1)的潮汐调和常数H、g值,按理论深度基准面的公式计算。当M4、MS4、M6三个浅海分潮振幅之和大于20 cm 时,还要进行浅水分潮改正”[9]。75 规范中考虑的分潮共计11 个,规范中未给出理论最低潮面具体算法。不考虑长周期分潮改正,保证了采用相同潮位数据计算结果的唯一性,但该算法降低了深度基准面的保证率。
1990 年,《海道测量规范》(GB 12327-90)(以下简称“90 规范”)规定:“以理论最低潮面作为深度基准面”[10]。同时,90 规范给出了理论最低潮面计算公式[10],除计算公式(明显不合理,应属排版疏漏)外,与《海道测量规范》(GB 12327-98)基本一致,在此不做详述。
1998 年,《海道测量规范》(GB 12327-1998)(以下简称“98 规范”)修正了90 规范理论最低潮面算法中的明显疏漏,是现行国家强制标准。98规范明确规定了用13 分潮计算理论最低潮面的计算公式[2],可概化如下:

98 规范算法是弗拉基方法的改进算法,改进后的计算结果有时会与原算法有较大差异,在做国外项目时应注意与当地的理论最低潮面算法的差别。
对比不同时期深度基准面算法之间的差异,将不同时期算法列于下表1:

表1 不同深度基准面算法对比
以下实例中,用2018~2019 年两年潮汐表[4]所载逐时潮位预报值进行调和分析,取得黄、渤海29 个站位的调和常数,分别按以上三种算法计算理论最低潮面,绘制与潮汐表采用值对比图(见图1)。其中的弗拉基方法,对比计算过程中均认为“平均海面季节变化较大”,“平均海面季节变化较小”情况与75 规范算法一致,不再单独列出。

图1 黄、渤海各站潮汐表与三种理论最低潮面算法结果对比
为方便显示黄、渤海各站三种规范算法计算结果与潮汐表所载理论最低潮面差异,绘制差值图见图2。
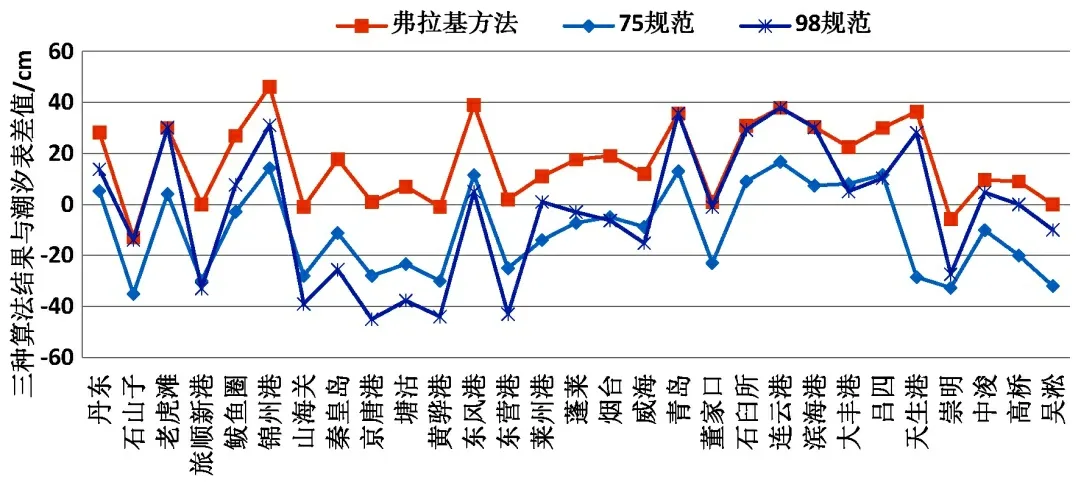
图2 黄、渤海各站三种理论最低潮面算法结果与潮汐表采用值差值
从以上计算及对比结果可以看出,大部分潮汐表采用值与98 规范规定算法计算结果存在明显差异,应非计算误差所致,而是采用了不同算法。
3.2 采用不同数据资料引起的差异
1)采用不同长度的潮位数据
采用不同长度的潮位数据,调和分析结果会有差异。一般情况下,采用的潮位数据资料越长,调和分析可靠性越高,理论最低潮面计算结果稳定性越好。
由于月球升交点作18.61 年周期变化,较多文献提出引入潮汐历元和深度基准面历元,长度为19 年。通常情况下,采用历元周期长度的潮位资料,既可以提高计算理论最低潮面的可靠性,也能修正非周期性变化影响。国际上,美国、澳大利亚等国均有潮汐历元和深度基准面历元长度的规定,如美国曾将潮汐和深度基准历元确定为1960~1978 年,2003 年起重定为1983~2001 年,长度为19 年;而澳大利亚潮汐和平均海面委员会建议采用的潮汐基准面历元为1992~2011 年,长度为20 年[11]。我国尚未有历元规定,为提高计算理论最低潮面的可靠性,可尽量增加采用的潮位资料长度。鉴于我国海平面上升引起的潮波改变、岸线及水下地形变化、局部地区潮差非周期性变化等因素,有条件时,宜分析理论最低潮面的非周期性变化趋势,确定适宜的理论最低潮面数值。
在此呼吁掌握长期潮位资料的权威部门,确定潮汐和深度基准面历元时段,并给出不同海域主港的历元时段平均海面、理论最低潮面和深度基准面保证率等数值,将会对规范国内深度基准面体系起到关键性作用。不宜变动深度基准面时,也会对评价采用的深度基准面提供依据。
2)采用不同时段的潮位数据
搜集夏威夷大学海平面中心(UHSLC)发布的连云港等8 站1975 年~1997 年连续23 年逐时实测潮位资料,分别以每年潮位资料为样本进行调和分析,然后分别以98 规范算法计算理论最低潮面,绘制各站理论最低潮面逐年计算结果见图3。

图3 各站1975 年~1997 年逐年潮位计算理论最低潮面结果
根据计算结果,统计各站23 年逐年计算理论最低潮面时,不同年份之间最大值、最小值和最大互差,并给出用23 年资料计算出的理论最低潮面,结果见表2。
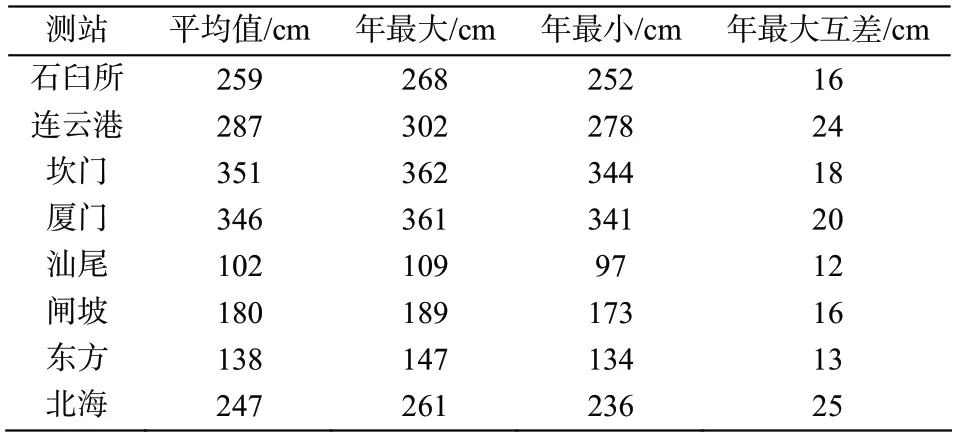
表2 各站23 年逐年计算理论最低潮面统计结果
通过对比分析可以看出,采用不同年份资料推算理论最低潮面可能出现明显差异,本例中按现行98 规范算法最大互差为25cm。
3.3 潮位观测位置变化引起的差异
长期潮位观测过程中,验潮站位置发生变化的情况时有发生,也有验潮站所在位置因工程建设导致潮汐特征改变情况出现。在变动前、后位置潮汐特征相似的情况下,为延长潮位资料序列,应进行变动前、后位置同步验潮,对原位置潮位资料进行必要订正。变动前、后位置潮汐性质变化较大情况下,应作为两个测站使用。
随着我国港口建设的发展,一些长期验潮站所在位置的潮汐性质因地形地貌变化(如在原本开敞环境下变为狭长通道内部情况)也会发生变化,进行潮汐分析时也要考虑。
3.4 调和分析的算法影响
调和分析的算法间接影响计算理论最低潮面结果。调和分析的算法中,能够分离出的调和分潮个数和方程组求解方法不同,都会造成计算结果差异。由于现在的潮汐调和分析理论已十分成熟,这类差异通常较小。
4 理论最低潮面计算结果检验
4.1 深度基准面保证率验证
深度基准面保证率是常用的评价海图深度基准面是否适宜的标准之一。
深度基准面保证率的计算公式为:
深度基准面保证率=高于深度基准面的低潮次数/低潮总次数×100 %。
通常认为深度基准面保证率的适宜数值为 95 %。也有深度基准面的保证率应大于98 %,特殊情况下不得小于95 %的说法[12],一般要求统计深度基准面保证率应有一年以上的水位观测资料。实际上,统计采用的资料越长,保证率的可靠性越高,遇到异常年份,仅采用一年水位资料统计深度基准面保证率可能产生较大偏差,这种情况在保证率较低时较明显。
4.2 附近港口或海域长期站采用值对照
计算理论最低潮面时,如附近港口或海域有长期潮位站,可与长期站采用值进行对照,必要时进行同步观测,与长期站潮位资料做相关分析,修正观测时段潮位代表性影响,以提高计算理论最低潮面的可靠性。
5 结语
通过以上分析,在当前形势下,建议按以下思路确定理论最低潮面:
1)确定理论最低潮面算法;
首先确定理论最低潮面的算法,以保证与附近港口或海域理论最低潮面算法协调一致。
2)计算理论最低潮面;
计算时应采用可靠的方法或软件。
3)采用的潮位资料的代表性分析和修正;
理论最低潮面计算结果应与附近港口或长期验潮站采用值进行对比分析,有条件应进行短期同步观测,通过相关分析等方法,确定采用的潮位资料的代表性,必要时应进行修正。
4)安全性评价。
对计算的理论最低潮面结果应进行安全性评价。安全性和与附近港口或海域采用值的协调性冲突时,应以安全性为重,重新确定算法。
总之,理论最低潮面的确定不应该是简单的计算,而是要在保证港口与航道安全的前提下,兼顾利用率,同时尽可能与附近港口或海域的采用值保持协调一致。
