基于改进的群论优化算法求解具有单连续变量背包问题

李香军，朱晓斌

（1.河北地质大学 信息工程学院，河北 石家庄 050031；2.石家庄文化传媒学校，河北 石家庄 050000）

0 引言

背包问题是一类重要的 NP难问题，其中包括 0-1背包问题[1]、带建制的背包问题[2]、折扣0-1背包问题[3]以及具有单连续变量背包问题（knapsack problem with a single continuous variable，KPC）[4]等多种类型的背包问题，在项目选择、网络阻截问题和资源配置等众多实际领域[5-8]都有重要的应用。KPC问题是由 Marchand和Wolsey[1]在1999年提出的一种带有连续变量的扩展 0-1背包问题，在物品生产、组织管理以及其他生产分配问题中有很高的应用价值。2011年，Lin等人[5]将 KPC问题分解为标准 0-1背包和伪背包问题，分别利用动态规划法和分支定界法进行求解。2012年，Buther和 Briskorn[6]利用构造法和启发式算法求解KPC问题。2018年，He等人[9]利用放缩法将KPC中的连续变量离散化，基于动态规划求解KPC问题。这些论文皆利用精确算法求解KPC问题，都具有时间复杂度过高的缺点。之后，He等人[10]在2018年引入了演化算法求解KPC问题的思想，建立了KPCM2和KPCM3两种新模型，并基于HBDE算法提出S-HBDE和B-HBDE算法分别求解这两种模型，此方法降低了时间复杂度，但求解效果欠佳。在 2019年，He等人[11]提出了ETDE算法，将背包的装载方案和连续变量作为一个个体，进一步提高了求解KPC问题的效率。近日，王泽昆等人[12]提出一个基于新颖S型转换函数的NBPSO算法求解KPC问题，提高了求解问题的精度与速度。利用演化算法求解KPC问题已经取得了不错的成果，所以利用演化算法求解KPC问题值得深入研究。

群论优化算法（Group theory-based optimization algorithm,GTOA）是He等人[13]在2018年提出的新颖算法，将代数群运算引入背包问题的进化过程中，将背包问题的可行解视为群的直积的一个元素，通过群的直积的乘法和逆运算来实现演化过程。GTOA算法在解决集合联盟背包问题、折扣{0-1}背包问题和有界背包问题上已有很好的结果。本文对 GTOA算法进行改进，基于KPCM2模型[10]求解KPC问题，对不可行解进行修复优化，给出求解KPC问题的一个新的高效的方法。

1 KPC定义与数学模型

KPC问题的描述如下[12]：给定物品集合N={1,2,…,n}和一个背包基本载重 C，物品j(j∈N)的价值为pj＞0，重量为wj＞0。在 KPC问题中，背包载重可变，添加了一个变量S进行调整，文献[10]基于降维法建立了模型KPCM2，消去了连续变量S，将解空间的维数从n+1降为n。KPCM2的数学模型如下：

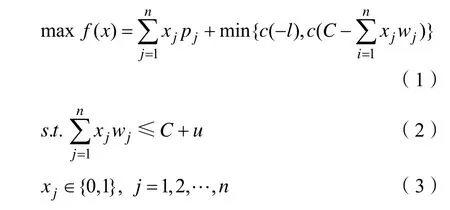
KPCM2数学模型更适于二进制演化算法求解KPC问题，减少了变量的数量，降低了求解的难度，所以本文基于 KPCM2模型求解 KPC问题。

2 GTOA 简介与改进

群论优化算法（Group theory-based optimization algorithm,GTOA）是利用Z/nZ的加法群（n为整数取得模，Z为整数集）生成群的直积来设计的一种新的进化算法。从代数观点看，无论背包问题属于哪一类，其可行解的每个分量都可以看作是Z/nZ可加群中的一个元素，可简化为Zn={0,1,…,n–1}，n其中n为正整数，n≥2。在此基础上，提出了一种代数方法来设计 EAs，并利用群的直积提出了一种基于群论的优化算法（GTOA）。GTOA算法可以直接求解整数规划问题，在离散空间[m1+1,m2+1,…,mn+1]上求解，[m1+1,m2+1,…,mn+1]={0,1,…,m1}×{0,1,…,m2}×…×{0,1,…,mn}，具有普适性，不仅易于实现，而且效率很高，适合于求解KPs。

GTOA算法主要包含随机线性组合算子（the Random Linear Combination Operator,RLCO）和变异算子。

RLCO算子：

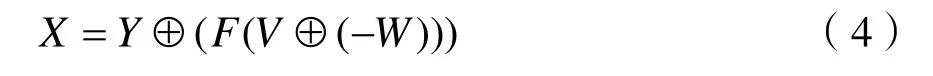
其中Y、V、W是群Z中随机选择的三个不同的元素，Y=(y1,y2,…,yn)，V=(v1,v2,…,vn)，W=(w1,w2,…,wn)，即种群中三个不同的个体，F=(f1,f2,…,fn)={–1,0,1}n是组合系数向量，为随机向量，X=(x1,x2,…,xn)是线性组合生成的新个体。新个体的产生为xj=yj⊕ [fj(vj⊕ (mj+1–wj))]，j=1,2,…,n。当m=1时，解空间为[2,2,…,2]={0,1}n。本文为求解KPC问题，KPC问题是0–1向量问题，所以解空间为[2,2,…,2]。

变异算子分为两种：反转与随机变异算子(the Inversion and Random Mutation Operator,IRMO)和选择变异算子（the Switch Mutation Operator,SMO）。当解空间为(m1+1,m2+1,…,mn+1)，md≥1，d=1,2,…,n时，使用IRMO算子，当解空间为(2,2,…,2)，使用 SMO 算子。由于本文是基于IGTOA算法求解KPC问题，所以使用的是SMO算子，伪代码描述本文不再赘述。

为了提升算法的全局搜索能力，本文将式（4）改为式（5），从而提出了IGTOA算法。

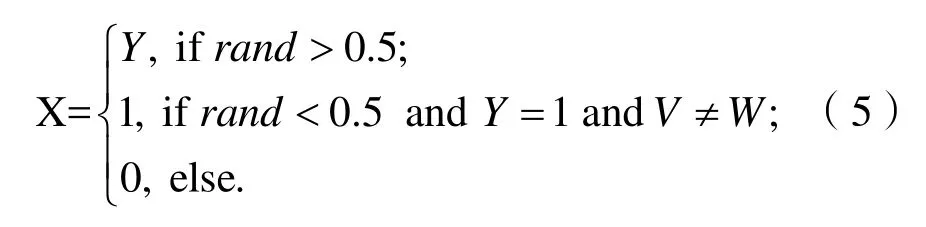
3 利用IGTOA求解KPC问题

由以上描述可得出IGTOA算法求解KPC问题的伪代码描述如算法1所示。

算法1 IGTOA算法。

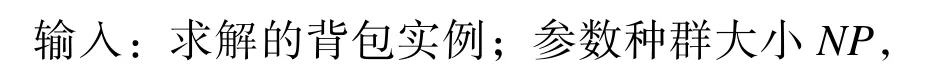
在算法1中，第1步的时间复杂度为O(NP*n)，M2-GROA算法的时间复杂度为O(n2)，令O(f)表示计算f(Xi)的时间复杂度，所以第2步时间复杂度为NP×O(f)+NP×O(n2)，第5步的时间复杂度为O(n)，第6步的时间复杂度为O(n)，第7步的时间复杂度为O(n2)，所以第 3～13步的时间复杂度为MIT×NP×(O(n)+O(n)+O(n2)+O(f))，故改进的GTOA算法的时间复杂度为O(NP×n)+NP×O(f)+NP×O(n2)+MIT×NP×(O(n)+O(n)+O(n2)+O(f))，当MIT、NP和O(f)是关于n的多项式时，此算法是多项式时间复杂度。

4 实验结果与分析

所有的计算均在配置为 Intel(R) Core(TM)i7-3770 CPU @ 3.40GHz和8GB内存的微型计算机上进行。操作系统为Windows 7旗舰版。本实验的编程语言为C，编译环境为Code:Blocks，使用Python语言绘制曲线图。

4.1 四类KPC实例

本文使用的实例为：逆强相关实例（ikpc）、强相关实例（skpc）、不相关实例（ukpc）、弱相关实例（wkpc），数据的规模为 100～2000，来自于文献[10]。

4.2 计算结果与分析

本节为 IGTOA、ETDE、S-HBDE、B-HBDE算法求解KPC实例的情况，并对这些实验结果进行分析比较。表1给出IGTOA、ETDE、S-HBDE、B-HBDE 4个算法的参数设置，其中NP为种群规模，n为问题实例的维数，MIT为迭代次数，Run为每个例子独立计算次数，CR为交叉因子，FS、F为缩放因子，ETDE、S-HBDE、B-HBDE中[–A,A]为问题每维的取值范围。

表1 IGT OA、ETDE、S-HBDE、B-HBDE算法参数设置Tab.1 The parameter settings of IGTOA、ETDE、S-HBDE and B-HBDE

记 Best、Average、Std分别为算法独立运行50次的得到结果的最好值、平均值、标准差，OPT为每类实例的最优值，表2～表5为各算法求解规模为100～1000的四类kpc实例的结果，其中加*号代表可以达到最优值，表现最好的用加粗标示。

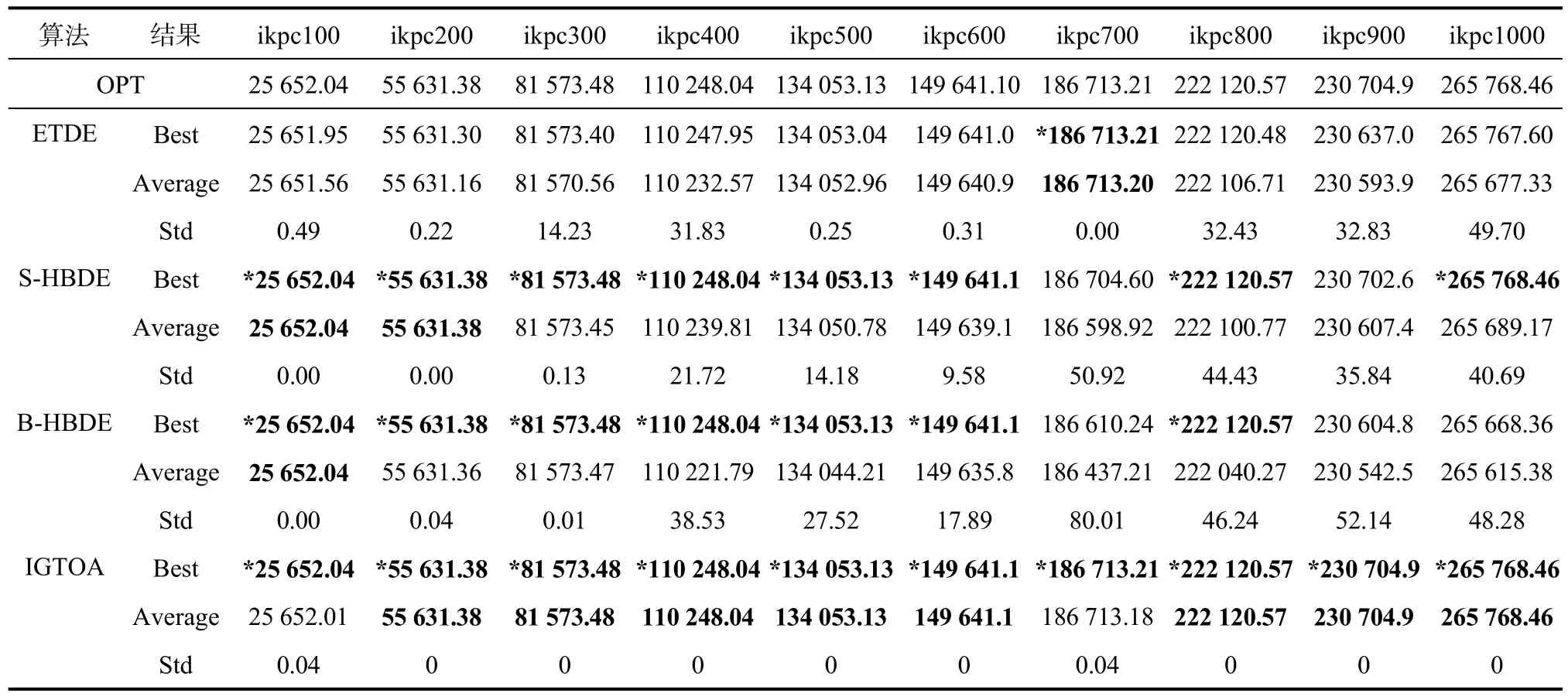
表2 ETDT、S-HBDE、B-HBDE和IGTOA求解ikpc类实例的计算结果Tab.2 ETDT 、S-HBDE、B-HBDE and IGTOA calculation results of ikpc class instances

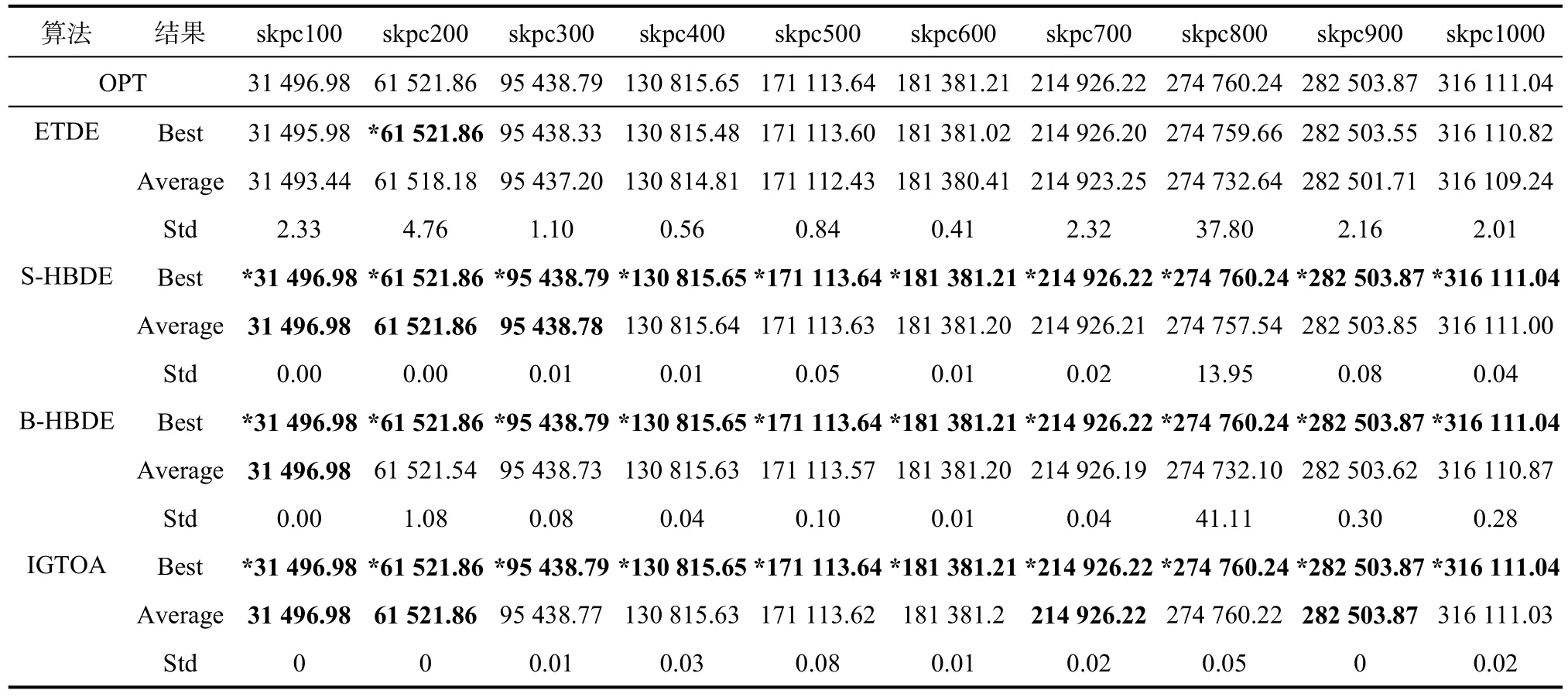
表3 ETDT、S-HBDE、B-HBDE和IGTOA求解skpc类实例的计算结果Tab.3 ETDT 、S-HBDE、B-HBDE and IGTOA calculation results of skpc class instances

表4 ETDT、S-HBDE、B-HBDE和IGTOA求解ukpc类实例的计算结果Tab.4 ETDT 、S-HBDE、B-HBDE and IGTOA calculation results of ukpc class instances

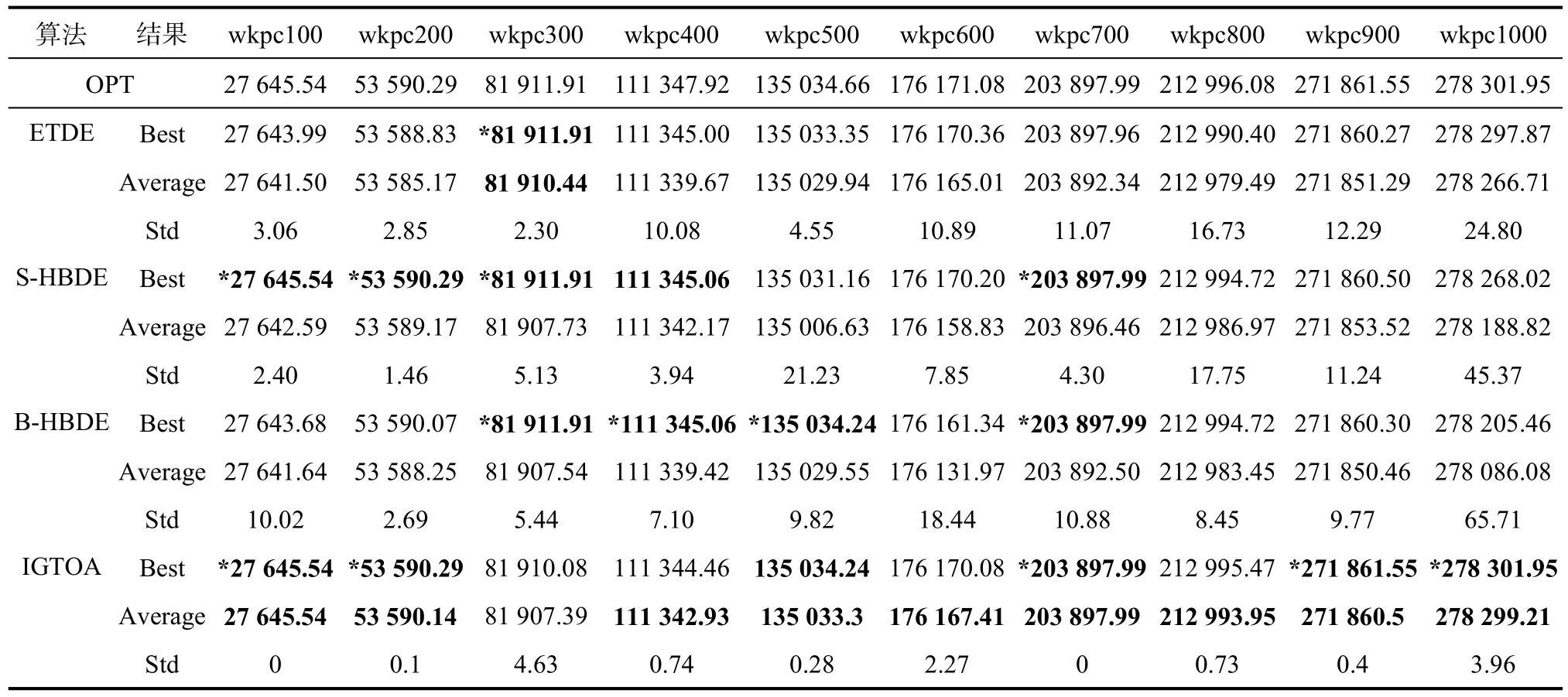
表5 ETDT、S-HBDE、B-HBDE和IGTOA求解wkpc类实例的计算结果Tab.5 ETDT 、S-HBDE、B-HBDE and IGTOA calculation results of wkpc class instances

从表2中可以看出，对于ikpc类实例，ETDT、S-HBDE、B-HBDE、IGTOA算法所求的最好值Best的个数分别为 1、8、7、10个，可以看出 IGTOA算法求解 ikpc类实例的精度最高；ETDT、S-HBDE、B-HBDE、IGTOA算法所求的平均值Average的个数分别为1、2、1、8个，所以IGTOA算法求解ikpc类实例的平均性能最好；而对于标准差Std，IGTOA算法求解的标准差10个实例里有 8个达到了 0，而其他算法只有一个或两个实例可以达到0，所以IGTOA算法求解问题的稳定性很好。总体而言，IGTOA算法求解ikpc类实例比其他算法都好，精度高，求解效果平均性能很好，稳定性最好。

从表3中可以看出，对于skpc类实例，ETDT、S-HBDE、B-HBDE、IGTOA 算法所求的最好值Best的个数分别为1、10、10、10个，可以看出ETDT算法求解 skpc类实例时精度最差，S-HBDE、B-HBDE、IGTOA算法10个实例都可以求解到最好值；ETDT、S-HBDE、B-HBDE、IGTOA算法所求的平均值Average的个数分别为0、3、1、4个，所以IGTOA算法求解skpc类实例的平均性能最好；而对于标准差 Std，IGTOA算法求解10个实例的标准差都几乎接近于0，其余算法求解问题的标准差略大，稳定性很好。总体而言，IGTOA算法求解 skpc类实例在精度上高于ETDT算法，和S-HBDE、B-HBDE算法精度相同，在平均性能和稳定性上比其他算法都好。

从表4中可以看出，对于ukpc类实例，ETDT、S-HBDE、B-HBDE、IGTOA 算法所求的最好值Best的个数分别为8、8、8、6个，ETDT算法求解ukpc类实例时在求解精度上略差于其他算法；ETDT、S-HBDE、B-HBDE、IGTOA算法所求的平均值Average的个数分别为3、3、2、6个，所以IGTOA算法求解ukpc类实例的平均性能最好，比其他算法都好；对于标准差 Std，IGTOA算法求解10个实例的标准差比其他算法小，其他算法求解问题的的标准差都较大，所以IGTOA算法求解问题稳定性最好。总体而言，IGTOA算法求解ukpc类实例在精度上比其他算法略差，在平均性能和稳定性上比其他算法都好。

从表5中可以看出，对于wkpc类实例，ETDT、S-HBDE、B-HBDE、IGTOA算法所求的最好值Best的个数分别为1、5、4、6个，ETDT算法求解 wkpc类实例时在求解精度上高于其他算法；ETDT、S-HBDE、B-HBDE、IGTOA算法所求的平均值Average的个数分别为1、0、0、9个，可以明显看出IGTOA算法的平均性能最好；对于标准差 Std，IGTOA算法也比其他算法小，稳定性很好。总体而言，IGTOA算法求解wkpc类实例在精度、平均性能和稳定性上比其他算法都好。

平均性能更能代表一个算法求解问题的效果如何，为了更直观的观察各算法的平均性能的好坏，图1给出了 ETDT、B-HBDE、S-HBDE、IGTOA算法求解 ikpc500、skpc500、ukpc500、wkpc500实例的平均收敛曲线图，从中可以看出，对于每一类实例，IGTOA算法都可以更快的求得最优解，所需要的时间最短，IGTOA算法在求解四类实例时收敛速度最快，在迭代150次之前基本就可以找到最优解，而其余算法都需要在迭代 150次之后才能找到最优解，所以，IGTOA算法比ETDT、S-HBDE、B-HBDE算法在求解kpc问题时效果好很多。

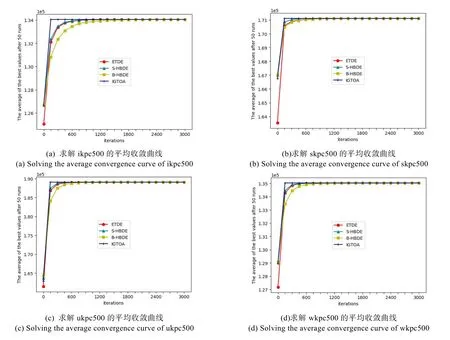
图1 ikpc500,skpc500,ukpc500和wkpc500实例的平均收敛曲线Fig.1 The average convergence curve of instance ikpc500, skpc500, ukpc500 and wkpc500

总体而言，IGTOA算法在求解 ikpc、wkpc类实例时在精度、平均性能、稳定性上比其他算法都好；在求解skpc类实例时，在求解精度上，比ETDT好，和S-HBDE、B-HBDE效果相当，在平均性能、稳定性上比其他算法都好；在求解ukpc类实例时，求解精度比 ETDT、S-HBDE、B-HBDE算法略差一些，但平均性能、稳定性上都高于其他算法，所以 IGTOA算法是一个求解KPC问题的高效算法。

5 总结

本文基于群论优化算法（GTOA)在模型KPCM2的基础上求解KPC问题，首先对GTOA算法进行改进，扩大算法的全局搜索范围，从而提出了改进的群论优化算法（IGTOA)。为了证明IGTOA算法在求解 KPC问题时效果更好，采用文献[10]中的40个实例进行验证，将IGTOA算法与ETDE、S-HBDE、B-HBDE算法的求解结果进行比较，表明IGTOA算法在求解KPC问题时，精度高、平均性能好、稳定性高、收敛速度很快，是一个求解 KPC问题的高效算法。由于 IGTOA算法是一种新颖的演化算法，在求解组合优化问题时仍需要探讨和研究，今后将尝试利用IGTOA算法求解其它整数规划问题，并进一步探讨将GTOA改进的高效方法。