白噪声作用下欠阻尼随机双稳系统中的随机共振

朱福成,郭 锋

(1.绵阳职业技术学院,四川 绵阳 621000;2.西南科技大学信息工程学院,四川 绵阳 621000)

0 引言

随机共振是一种出现在随机动力系统中的非线性现象，即在弱周期力的作用下，由噪声诱导的系统势井间的跳跃同步行为[1]。对于随机非线性系统而言，这种同步依赖于噪声和周期外力间的协同作用。因此，系统非线性、驱动力的周期性、噪声3个因素是非线性系统出现随机共振现象的必要条件。阻尼指由于外部作用或系统内在原因而使振动系统振幅逐渐减小的物理现象。对于足够大的阻尼力，系统处于过阻尼状态；否则，系统处于临界阻尼或欠阻尼状态。对于过阻尼条件下的动力系统，其惯性项可以忽略。但是，对于中、小阻尼系统，由于惯性效应不可忽略而应建立相应的欠阻尼模型。自随机共振现象发现以来，过阻尼非线性系统中的随机共振受到学者们的广泛关注。文献[2]分析了过阻尼分数阶Langevin方程产生随机共振的内在机理。文献[3]研究了过阻尼双稳系统在α噪声作用下出现随机共振的不同特征。文献[4]利用过阻尼Langevin方程来描述企业的随机动力学行为，认为内外部资本环境的随机波动产生了统计意义上的最大随机激励效应。文献[5]～[7]研究发现过阻尼生物模型中也会出现随机共振现象。文献[8]～[10]将过阻尼双稳系统中的随机共振用于故障诊断和微弱信号检测中。同时，欠阻尼动力系统中的随机共振也得到了深入研究。文献[11]研究了二阶欠阻尼线性谐振子的稳态响应，给出了由质量及频率涨落噪声诱导而出现随机共振现象的充分必要条件。文献[12]讨论了欠阻尼双稳系统中噪声强度、强迫频率对系统响应的影响。文献[13]研究表明，增加双值噪声非对称参数和阻尼参数可以抑制欠阻尼系统的随机共振现象。文献[14]分析了泊松白噪声作用下耦合欠阻尼双稳态系统的随机共振行为。文献[15]研究发现，欠阻尼系统输出在一二次谐波处的信噪比随着噪声强度的增加呈现出先最小后最大的变化规律。文献[16]发现欠阻尼三阱势系统存在两个临界阻尼值，分别会导致随机共振的出现和消失。

上述文献均基于系统具有确定性势能函数的情形；在某些情况下，环境的扰动会干扰系统的势能函数，从而势能函数应该按随机势能建模。文献[17]分析了受位置随机扰动的过阻尼布朗粒子在周期势中的运动，发现随着随机势幅度的增加，概率流的最大值减小。文献[18]研究发现，随机势对输运过程的影响随随机势振幅和随机势相关长度的增大而增大。文献[19]研究发现，随着双稳态系统随机势强度的增加，信噪比存在多个峰值到没有峰值的转变。文献[20]、[21]研究表明，在随机双稳系统的信噪比与噪声强度、静态力的关系曲线上出现了随机共振现象。文献[22]在具有波动势垒的蛋白质—马达系统中发现了系统的随机共振行为。

1 随机双稳系统的输出信噪比

考虑二阶随机系统(1)

(1)

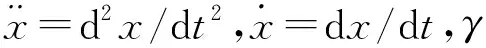
〈η(t)〉=0,〈η(t1)η(t2)〉=2Dδ(t1-t2)。

(2)

势能函数为

(3)

其中，U0(x)为确定性势能部分,ξ(x)为小的态变量扰动，即势能U(x)的随机部分,其取值为±Δ,沿一维空间随机跳跃。ξ(x)可以用一个随机函数n(x2,x1)表示,它表示在x=x1和x=x2坐标范围内在+Δ和-Δ两个数值间跳跃的次数。n(x,0)服从Poisson分布。

(4)

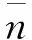
(5)

其中，L是相关长度。ξ(x)的均值和相关函数分别为

(6)

对于单一双值势能，有：

(7)

(8)

(9)

(10)

随机势ξi(x)的统计特性为

(11)

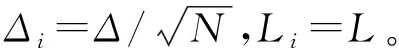
(12)

(13)

在极限N→∞下,有：

(14)

容易看出，单一双值势能的统计特性与Ornstein-Uhlenbeck势能类似，本文仅考虑Ornstein-Uhlenbeck势能。

(15)

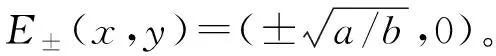
(16)

由方程(16),系统的准稳态概率密度可以表示为

(17)

(18)

设系统满足绝热近似条件[1],即驱动周期力的频率Ω低于系统在某个势井内的弛豫速率,则系统有足够时间在一个周期T=2π/Ω的时间内达到局域平衡。由式(16),绝热近似条件下系统在两稳态E±间的转移率可以表示为

(19)

W±(t)=f(α+βcos(Ωt))

(20)

可展开为

(21)

其中，

(22)

W0是系统(1)仅受噪声作用时的Kramers速率。

(23)

(24)

对系统输出信号的自相关函数进行傅里叶变换得到的系统输出功率谱可以表示为

S(ω)=S1(ω)δ(ω-Ω)+S2(ω)

(25)

其中等式右端两项分别为信号和噪声的功率谱，系统输出信噪比(SNR)定义为信号功率与信号频率处噪声功率的比值，可以表示为

(26)

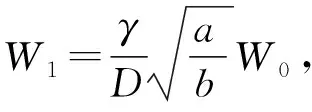
(27)

在本文后续的讨论中，参数设置满足该条件。

2 讨论

当阻尼比较小时，系统为欠阻尼系统。而当随机扰动作用在系统态变量时，系统势能函数变成随机函数。本文分析白噪声作用下欠阻尼随机双稳系统中的随机共振现象，基于Fokker-Planck方程,我们推导出稳态概率密度的表达式。利用两态理论，求得系统输出信噪比SNR的解析表达式。下面，基于式(26)来分析SNR与系统参数、噪声参数及随机势能参数的依赖关系。

由图1～图4可见,在信噪比SNR与阻尼系数γ的关系曲线上出现了一个共振峰，即广义的随机共振现象。有必要指出，SNR与阻尼系数间的单峰现象是一个新的结果，在文献[19]～[23]的欠阻尼系统中没有研究过。同时，该非单调现象与欠阻尼线性系统中出现的现象显然不同。对欠阻尼线性系统而言，系统输出信号随阻尼的增大而单调减小。该现象可以解释为系统与噪声间的非线性作用导致系统转移率W±与阻尼系数有关，从而可能在某个阻尼系数时，输出信号达到最大。由图1容易发现，随着系统参数a的增大,SNR向小的γ值方向移动，故对于较小的γ值,应该参数a选择大的值以提升系统输出信号。同时，比较图1与图2可见,系统参数b对SNR的影响与参数a对其影响不同。随着参数b增大,共振峰向大的γ值方向移动,故对于大的参数b,较大的阻尼系数γ可以提升系统输出性能。图3表明，对于较大的噪声强度D,相对较大的γ值可以提高系统输出性能。随着随机势幅度Δ的增大，SNR的峰值高度单调增大，如图4所示。

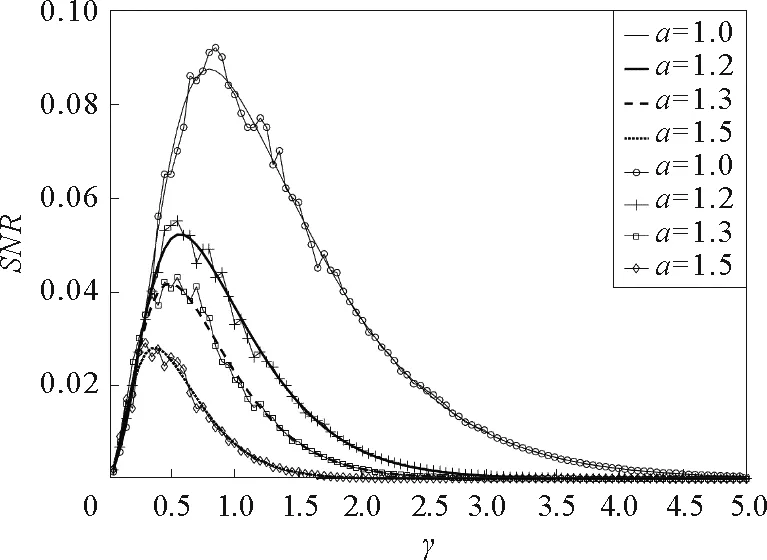
参数b=1,Δ=0.2,D=0.1,L=10,A=0.2,Ω=0.1图1 系统参数a取不同值时信噪比SNR与阻尼系数γ的关系曲线

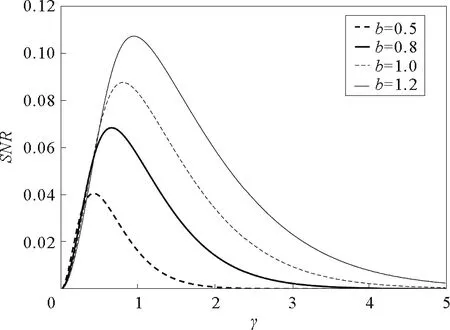
参数a=1,Δ=0.2,D=0.1,L=10,A=0.2,Ω=0.1图2 系统参数b取不同值时信噪比SNR与阻尼系数γ的关系曲线

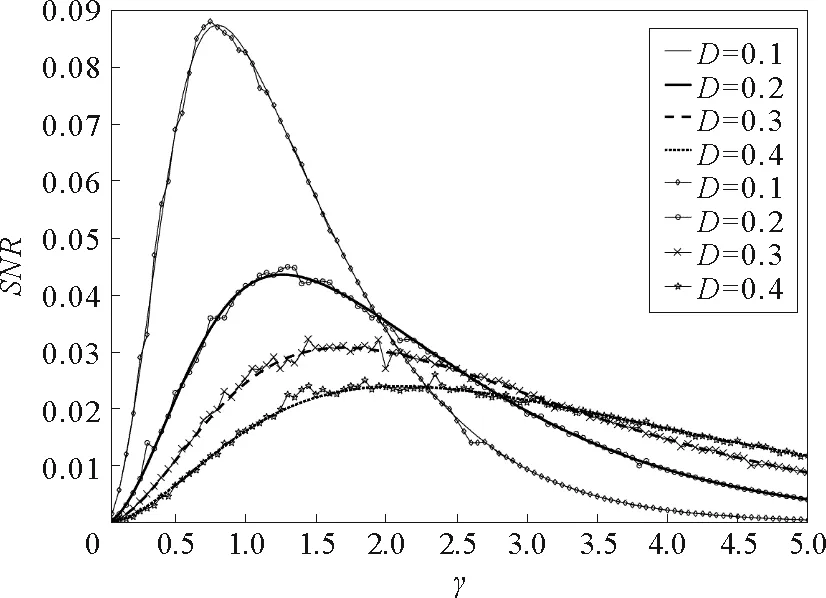
参数a=1,b=1,Δ=0.2,L=10,A=0.2,Ω=0.1图3 噪声强度D取不同值时，信噪比SNR与阻尼系数γ的关系曲线

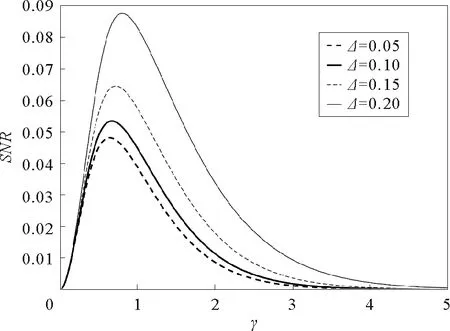
参数a=1,b=1,D=0.1,L=10,A=0.2,Ω=0.1图4 随机势能的幅度Δ取不同值时，信噪比SNR与阻尼系数γ的关系曲线

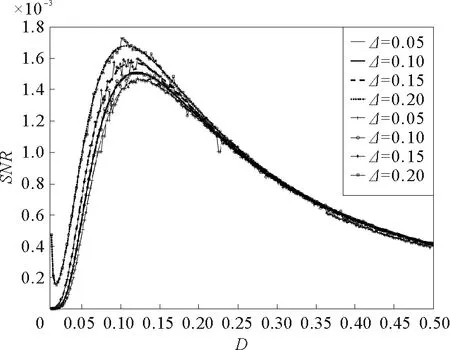
参数γ=0.1,a=1,b=0.1,L=10,A=0.1,Ω=0.1图5 随机势能的幅度Δ取不同值时，信噪比SNR与噪声强度D的关系曲线

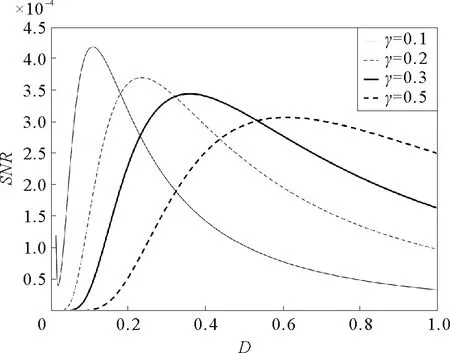
参数a=1,b=0.1,Δ=0.2,L=10,A=0.05,Ω=0.1图6 阻尼系数γ取不同值时，信噪比SNR与噪声强度D的关系曲线

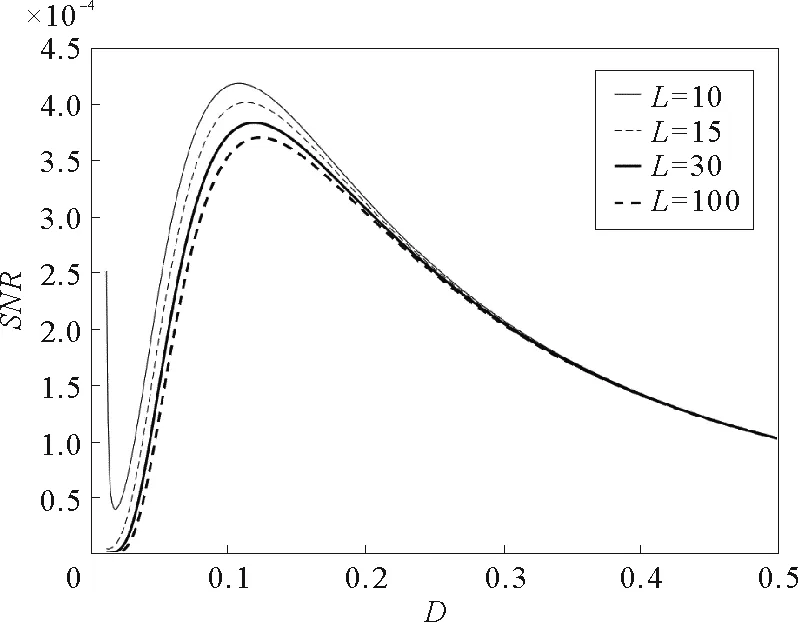
参数γ=0.1,a=1,b=0.1,Δ=0.2,A=0.05,Ω=0.1图7 随机势能的相关长度L取不同值时，信噪比SNR与噪声强度D的关系曲线

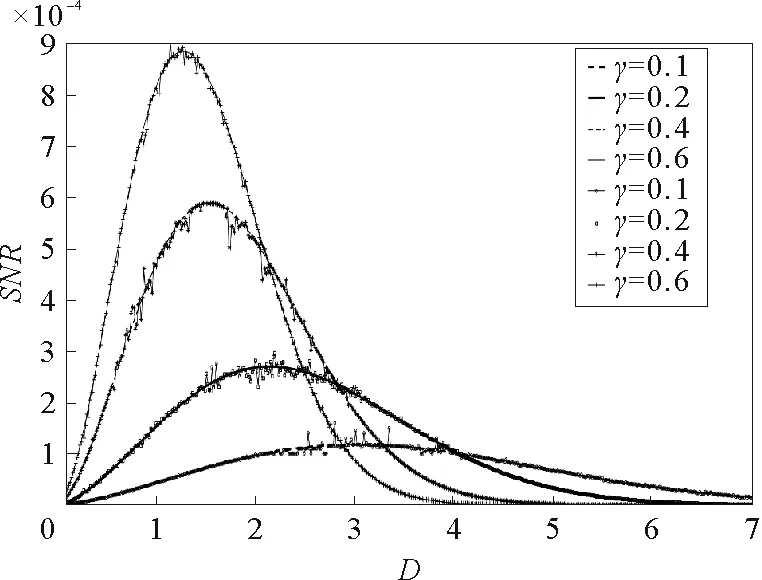
参数b=1,Δ=0.1,D=0.3,L=10,A=0.05,Ω=0.1图8 阻尼系数γ取不同值时，信噪比SNR与系统参数a的关系曲线

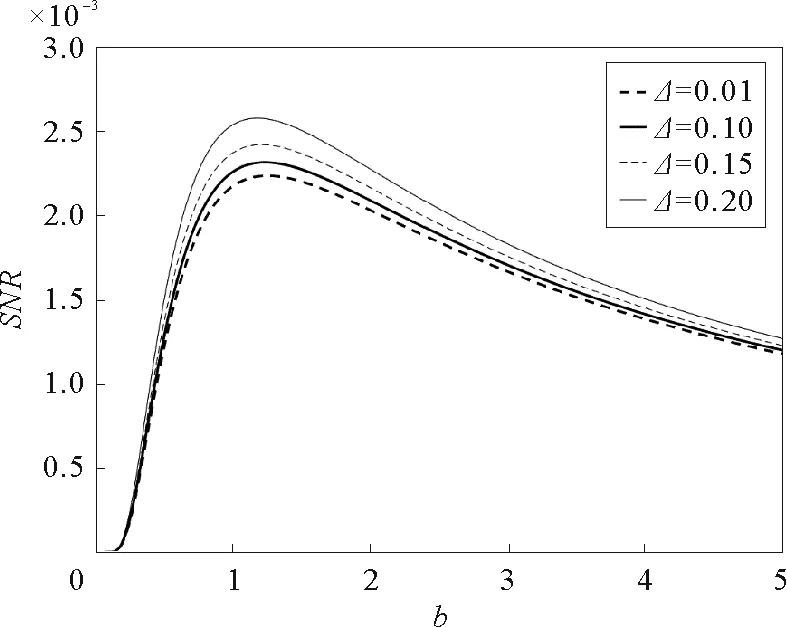
参数γ=0.1,a=2,D=0.08,L=10,A=0.1,Ω=0.1图9 随机势能的幅度Δ取不同值时，信噪比SNR与系统参数b的关系曲线

为了验证理论分析的正确性，我们对采用四阶龙格—库塔法对方程(1)进行了数值积分,计算步长为0.001。对自相关函数进行快速傅里叶变换得到输出信号的功率谱，输出信噪比定义为信号的频谱与信号频率附近噪声功率谱的比值，部分仿真结果见图1、图3、图5和图8。由这4个图可见，本文基于绝热近似的理论分析结果和数值仿真结果是一致的。

3 结论

本文研究了白噪声作用下欠阻尼随机双稳系统中的随机共振现象。随机势能用Ornstein-Uhlenbeck噪声建模。基于Ornstein-Uhlenbeck噪声的统计特性和两态理论,推导出了系统输出信噪比的表达式。分析结果表明，在信噪比与阻尼系数的关系曲线上出现了广义的随机共振现象。在信噪比随噪声强度的变化曲线上观察到了传统的随机共振现象。而且，随着系统参数a和b的增大，信噪比也出现了共振峰。随着随机势能相关长度的增大,信噪比的最大值单调减小；而随着随机势能幅值的增大,信噪比的最大值单调增大。最后利用龙格—库塔法对系统输出信噪比进行了数值仿真。仿真结果表明，理论结论与数值分析结果是一致的。我们认为，本文研究的数学模型可以拓展双稳系统中随机共振的研究范围；本文的研究结果对于具有随机势能的动力系统中的随机共振分析具有一定的理论意义和参考价值。