失配参数在线矫正的永磁同步电机预测电流控制
2021-06-19高锋阳罗引航李明明王文祥张浩然
高锋阳,罗引航,李明明,王文祥,张浩然
(兰州交通大学自动化与电气工程学院,甘肃兰州 730070)
1 引言
永磁同步电机(permanent magnet synchronous motor,PMSM)具有高效节能,结构多样化,起动力矩大等优点,已经在石油工业、轨道交通、家电行业等领域得到广泛应用[1–2].目前,模型预测控制(model predictive control,MPC)以优化规则灵活、鲁棒性能好、易于处理非线性多变量问题等优点成为电机控制领域研究的热点[3–5].
永磁同步电机模型预测控制是一种比较依赖于参数的控制算法.模型失配会降低电机控制的精度以及准确度,引起矢量作用时间出现计算误差等问题[6–8].目前,针对模型失配引起的MPC策略性能下降问题,诸多学者提出了多种应对策略:①将辨识得到的电机参数对预测模型参数进行实时矫正[9].采用最小二乘法辨识电机参数,但最小二乘法计算耗时长,不适合实时辨识[10–11].文献[12]将最小二乘法转化成递推算法,辨识过程不需要存储所有数据,可实现在线辨识.然而递推最小二乘法对时变环境跟踪性能差,容易受到噪声影响,可能引起模型参数估计误差增大.②预测控制与智能控制结合.基于神经网络误差修正的预测控制能较好抑制模型失配,但神经网络收敛速度较慢,当工况变化时不能很快地适应环境[13–14].把模型失配引起的误差采用模糊推理进行反馈校正[15–16],但模糊控制设计缺乏系统性.③预先估计出模型失配引起的预测误差,并将预测误差补偿到模型预测控制策略中[17–18].通过建立每个环节的误差模型以及各环节间误差的传递关系,形成各环节独立的误差补偿方案.但估计预测误差增大了系统的计算负担,降低了系统的效率.
为了改善电机模型失配引起的预测控制性能下降问题,在PMSM的三矢量模型预测电流控制(model predictive current control,MPCC)基础上,提出一种基于内模控制(internal model control,IMC)观测器的应对模型失配策略[19].首先,根据旋转正交坐标系下的PMSM动态模型,设计内模控制观测器,估计d,q轴电流变化率,并在线进行电机参数估计;然后,利用卡尔曼滤波减弱参数估计噪声,采取参数阈值化处理对模型参数进行在线矫正,以提高模型失配工况下系统的控制性能;最后,实验分析了不同模型参数失配的程度高低对系统性能的影响.将所提策略应用于PMSM三矢量MPCC,实验表明本文策略可以实时矫正失配参数,提高系统鲁棒性.
2 PMSM的三矢量模型预测电流控制
2.1 PMSM的数学模型
表贴式永磁同步电机在旋转正交坐标系(d–q)中的模型表达式为

式中:Ld,Lq分别为定子电感的直、交轴分量,且Ld=Lq=L;id,iq,ud,uq分别为定子电流和电压的直、交轴分量;R为定子电阻;ωe为转子电角速度;ψf为转子永磁体磁链.
根据式(1),以定子电流作为状态变量,可建立状态空间模型为
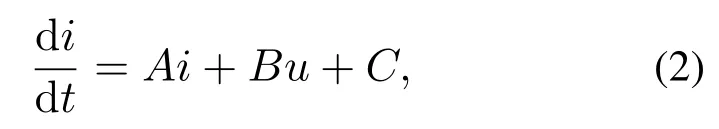
式中:
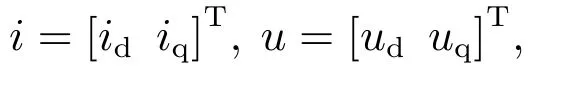
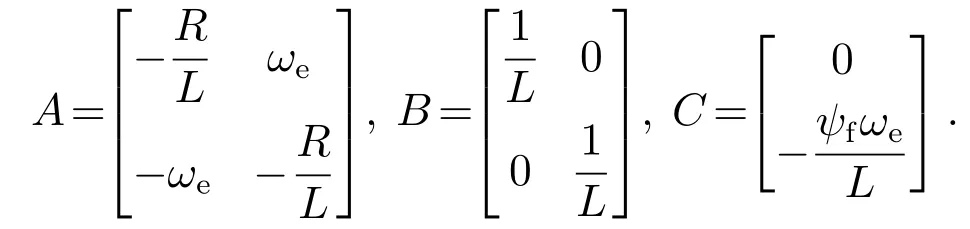
2.2 三矢量MPCC原理
三矢量指3个基本空间电压矢量,包括两个有效电压矢量和一个零矢量.有效电压矢量包括(100),(110),(010),(011),(001)和(101).零矢量包括(000)和(111).
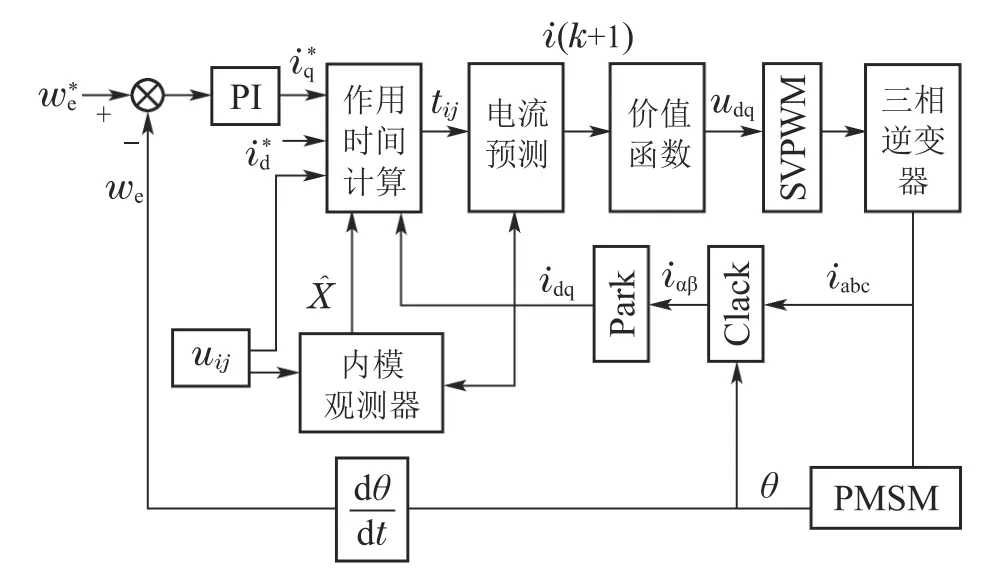
PMSM三矢量MPCC结构框图如图1所示,主要由电流预测、矢量作用时间计算、价值函数选优等模块组成.系统给定电流=0,给定电流为速度环比例积分(proportional integral,PI)控制器输出.其中,ui,uj为两个有效电压矢量,两个有效电压矢量和零矢量的合成电压矢量udq为PMSM的控制量.

图1 三矢量模型预测电流控制系统框图Fig.1 Block diagram of the three-vector-based model predictive current control system
2.3 电流预测
对状态方程式(2)采用欧拉法可得到离散化的d,q轴电流预测表达式为

式中:i(k)为第k个周期的电流采样值;i(k+1)为第k+1个周期的电流预测值;Ts为采样周期;u(k)为第k个周期的电压采样值;ωe(k)为第k个周期转子电角速度的采样值.
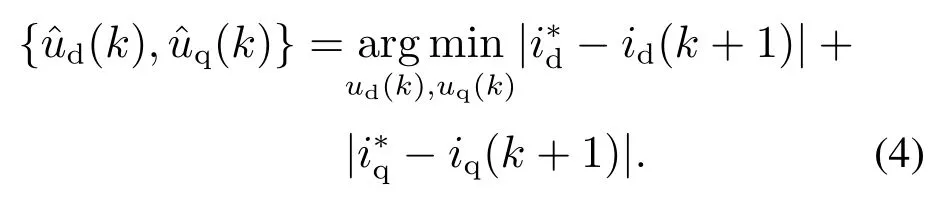
2.4 三矢量作用时间计算
根据式(1)可知,令u=u0=[0 0]T,可得零矢量出力时,直、交轴电流变化率表达式为

可得有效电压矢量出力时,直、交轴电流变化率表达式分别为
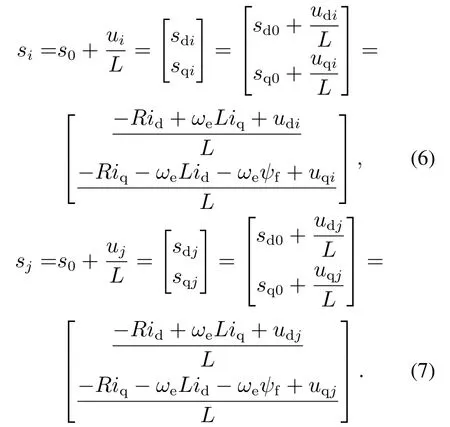
系统要使下一个采样时刻直、交轴电流等于给定电流,则根据无差拍控制原理,直、交轴电流预测表达式可以写为
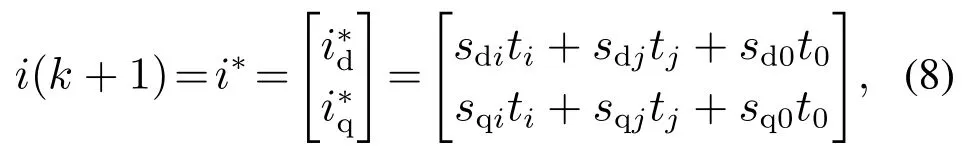
式中ti,tj,t0分别为ui,uj,u0的作用时间.
在不考虑死区时间等理想情况下,一个周期的采样时间Ts全部分配给了ui,uj,u0的作用时间,即
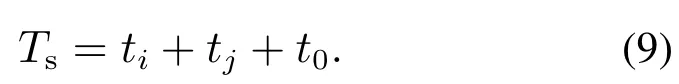
根据式(7)–(8),可求得ti,tj,t0的表达式分别为
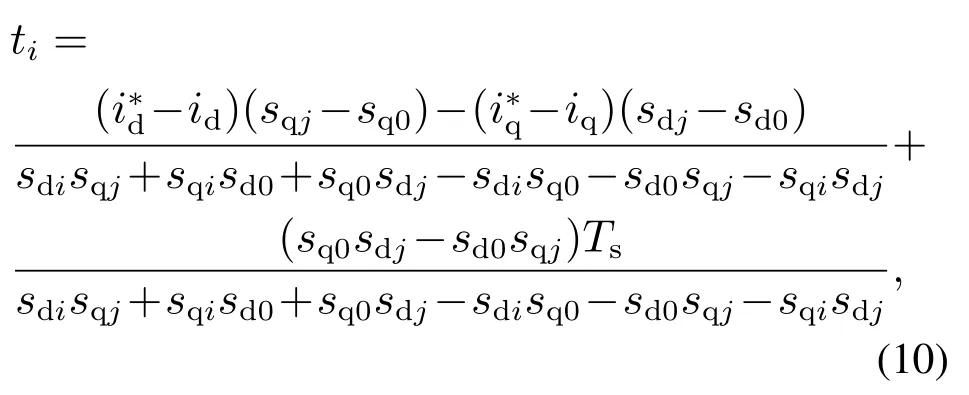

在电机启动的暂态过程中,可能会出现ti,tj,t0不在0∼Ts的情况.当ti,tj,t0不在0∼Ts时,则需要对ti,tj,t0重新进行分配.具体分为以下4种情况:
1) 当ti <0,tj <0,则令ti=0,tj=0,t0=Ts.
2) 当ti >0,tj >0,t0<0,则令
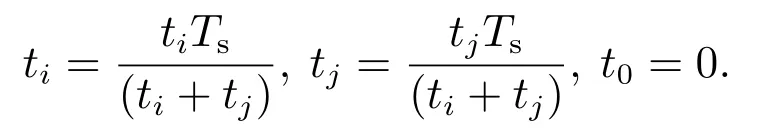
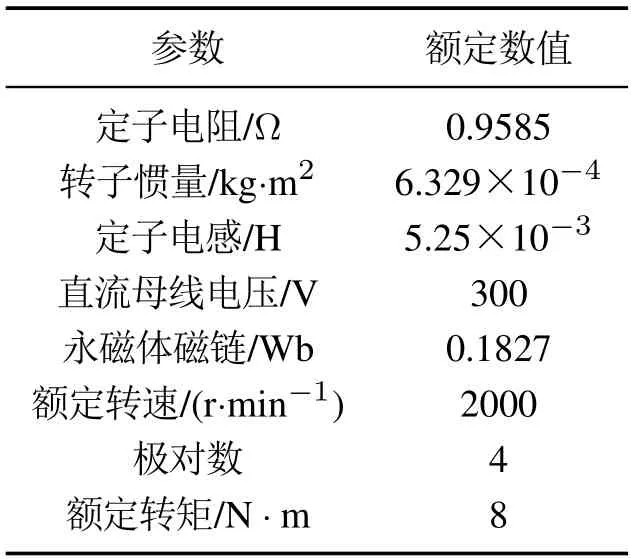
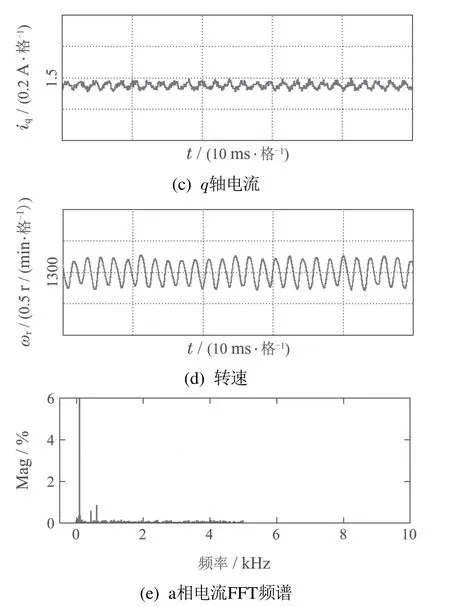
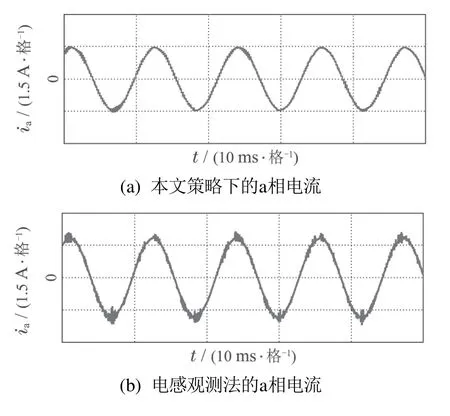
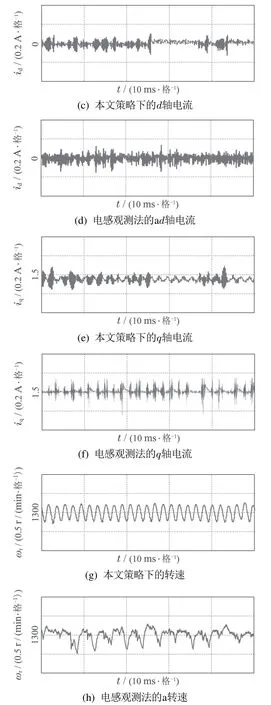
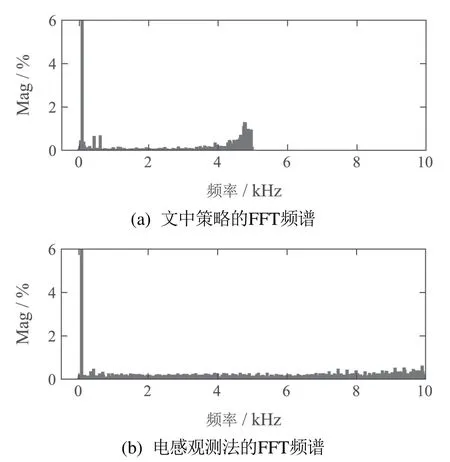
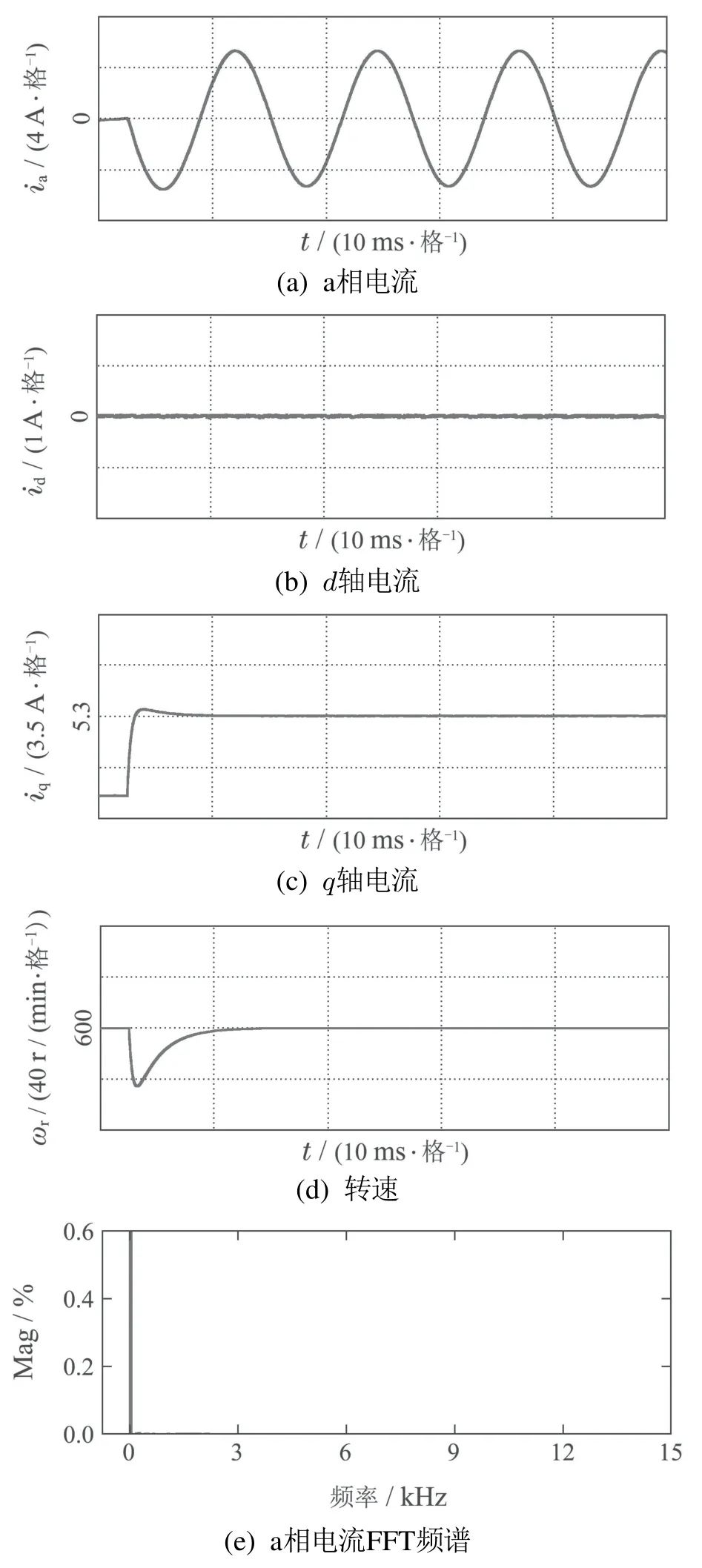
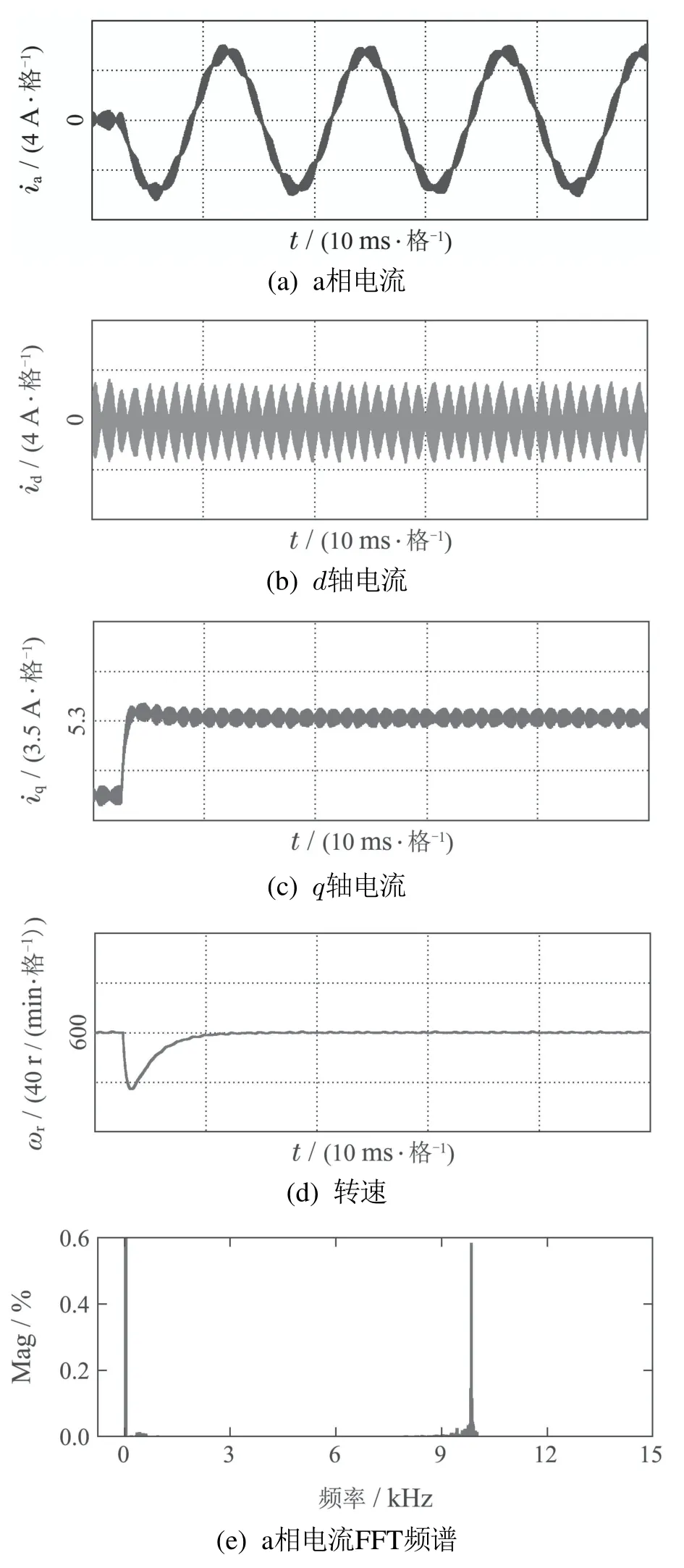
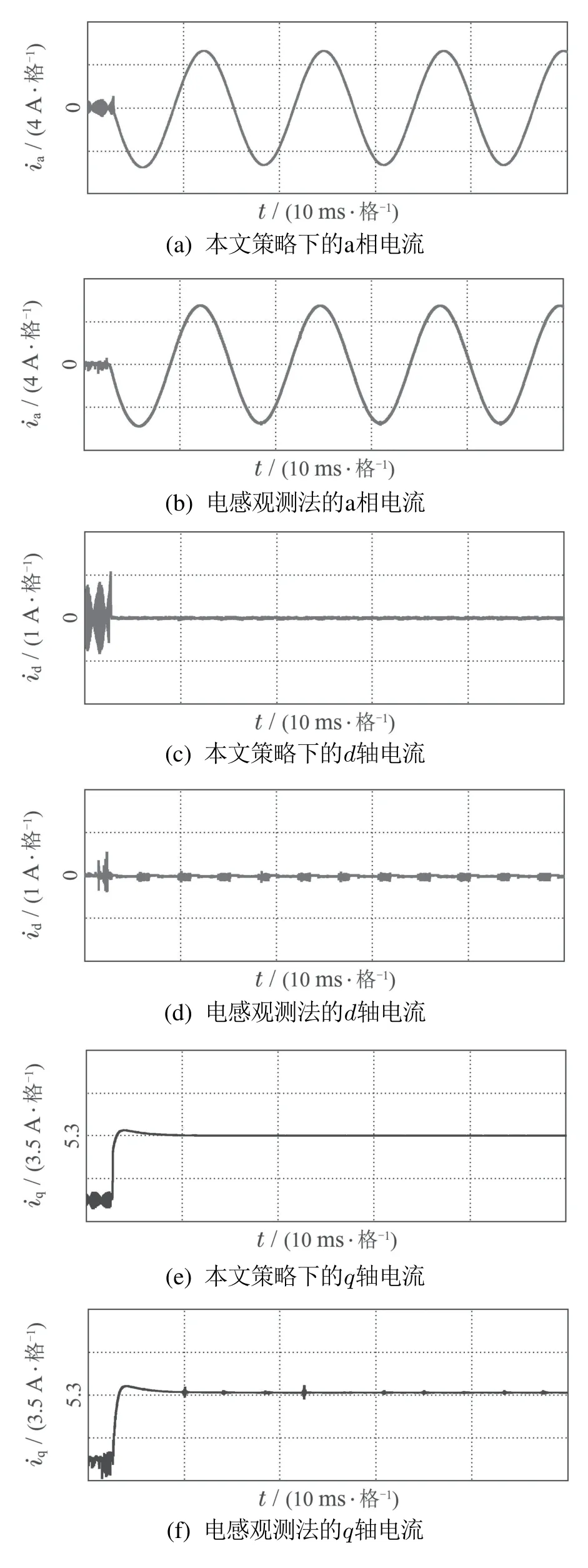
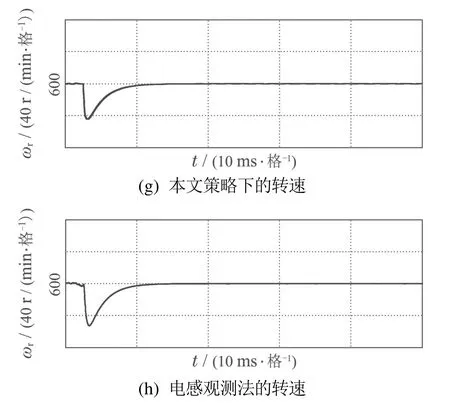
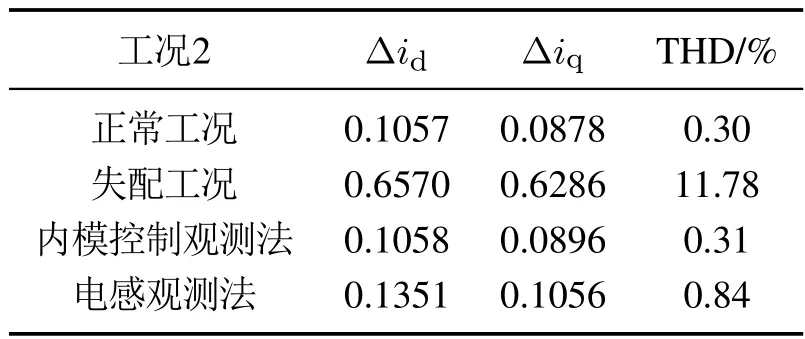
3) 当ti <0,0 4) 当ti <0,tj>Ts,则令ti=0,tj=Ts,t0=0;或者tj <0,ti >Ts,则令ti=Ts,tj=0,t0=0. 根据电压矢量的合成法则,可得直、交轴上的期望电压矢量.由式(13)–(14)分别计算出期望电压矢量在直、交轴上的分量. 由式(12)–(13)和其它量代入式(3)可以计算出下一采样时刻的电流预测值id(k+1),iq(k+1). 三矢量MPCC将定子电流直、交轴分量作为控制参数,为了评价控制效果的有效程度,构造了价值函数式(14)作为控制有效性的评判依据. 价值函数值越小,则表明预测电流越接近给定电流,控制性能越好;价值函数值越大,则表明预测电流越偏离给定电流,控制性能越差.通过式(14)筛选出控制效果最优的基本电压矢量组. 实际工况中,控制系统难免会存在参数扰动,如控制系统的模型与实际系统之间的模型失配问题.这种问题使得基于算法的模型预测轨迹与实际系统运行轨迹存在偏差,这可能会引起系统性能变差甚至系统失稳的后果.下面针对模型参数失配的问题引入一种基于IMC的观测器.当电机实际参数发生变化时,表贴式永磁同步电机的数学模型可重新表示为 式中:L,R,ψf分别为定子电感、定子电阻、永磁体磁链的模型参数;∆L,∆R,∆ψf为相应模型参数的偏差量. 定义fd,fq分别为模型失配系统的d,q轴电流变化率的偏差值. 则式(16)可以简写为 在式(18)中,以id为状态变量,建立状态方程为 式中: 在式(20)中,系数a,b易求得.构造原系统的状态估计系统.状态估计系数取原系统系数,状态估计方程为 由式(23)–(24)构成状态空间方程组为 式中:k1,k2为待设计参数.通过合理地设计k1,k2的值改变系统的特性.当控制系统的采样周期Ts较小时,假设参数d值不变,即有˙d=0.则式(26)可进一步表示为 可由特征方程det[sI−(A−BK)]=0求得状态反馈系统的特征根. 由式(21)和式(29)构成IMC观测器d轴电流方程组,即 显然,IMC观测器可做到无静差估计原系统的状态变量. 同理,IMC观测器q轴电流方程组与d轴相似,其具体方程组为 图2 d,q轴的IMC观测器结构框图Fig.2 Structure diagram of d–q axis internal model control observe 永磁同步电机电磁转矩与定子电流的关系表达式为 式中:Te为电磁转矩;ψf为永磁体磁链;Pn为电机极对数;iq为q轴定子电流. IMC观测器的连续量采用零阶保持器法离散化.由式(1)(32)可得转子磁链、定子电感、定子电阻在k时刻的估计表达式为 在实际应用中,对电机参数进行估计时,常常会受到内外界的干扰,这会导致干扰信号叠加于有用信号,这就需要从参数估计数据中消除或减弱干扰噪声,提取最优参数估计.文中采用卡尔曼滤波获取最优参数估计. 考虑滤波系统没有控制量,离散的卡尔曼滤波系统方程可以简化为 式中:xk为离散时间序列k的参数估计向量;zk为离散时间序列k的观测向量;矩阵A和矩阵H都是已知方阵;向量wk和向量vk分别表示过程噪声、观测噪声. 矩阵A和矩阵H在实际工况中都可能随环境变化而变化,但在文中设定为常数. 定义矩阵Q为过程噪声协方差,矩阵R观测噪声协方差.实际过程中,Q和R可能随着每次在线计算而变化,但在文中设定它们为常数. 假设噪声信号wk是满足正态分布的白噪声,即 设定卡尔曼滤波的滤波、协方差初值后,计算过程可分为以下步骤: 为了避免系统频繁得更新模型参数而引起的参数摄动,提出一种阈值化处理的模型失配参数矫正方法.选择某一阈值,如果参数估计大于或小于该阈值,则系统保持原模型参数运行;如果参数估计小于或大于该阈值,则需要对系统模型参数进行在线更新.参数阈值化处理的数学表达式为 易知,选用不同的阈值其处理效果也会不同.选用阈值过大,则即使系统处在较严重模型失配情况下,系统模型参数仍得不到在线矫正;选用阈值过小,则系统频繁得在线更新模型参数,易受外界环境干扰. 3种模型参数失配对系统的影响作一个定性分析:由式(5)–(7)知,当ψf比电机实际值小,会引起sq0偏大;当L比电机实际值小,会引起sq0偏小,si和sj偏大或偏小;当R比电机实际值大,会引起sq0偏小.可见,L失配引起的不确定性最大,对系统的控制性能影响也最大,ψf与R失配影响较小,且ψf与R同时失配时,对sq0影响有一定的抵消作用,甚至可以忽略.经多次仿真实验,初步设定各参数的阈值,各参数阈值化处理的数学表达式为 将阈值化处理后的模型参数传递给作用时间计算模块,以此来减弱模型失配引起的模型预测轨迹与系统实际运行轨迹的偏差. 基于IMC观测器应对模型失配策略框图如图3所示.以模型参数X为例,从电机采样定子电流得到d,q轴电流,并估计电流变化率求得参数估计,通过卡尔曼滤波减小参数估计扰动,得到最优参数估计,然后将最优参数估计经阈值化处理后传递给MPC模块,预测下一个采样周期内最优的开关管状态,从而让输出电流尽可能得接近给定电流. 图3 基于内模控制观测器应对模型失配策略框图Fig.3 Block diagram of model mismatch strategy based on internal model control observer 基于IMC观测器的PMSM三矢量MPCC框图如图4所示,与传统PMSM三矢量MPCC系统不同的是,其引入IMC观测器在线估计参数,用处理后的参数估计更新模型失配参数. 图4 基于内模控制观测器模型预测电流控制框图Fig.4 Block diagram of model predictive current control based on internal model control observer 在实际工况中,定子温升引起定子电阻增大,定子电流上升造成定子电感值减小,以及电机长时间运行可能出现永磁体磁链减小.为验证本文所提策略应对电机模型失配的有效性,本节在两种不同工况下,分别对每种工况的3种不同情况进行实验验证.实验被控对象为表贴式PMSM,其参数额定值见表1,d,q轴电流IMC观测器的参数均为k1=−32000和k2=50.卡尔曼滤波系统取Q=0.0003,取R=5.这里电机的定子a相电流,d轴电流,q轴电流,转子转速,电磁转矩分别记为ia,id,iq,ωr,Te. 表1 永磁同步电机参数Table 1 Parameters of PMSM 工况1电机稳态运行过程中,给定的转速为1300 r/min;给定负载转矩为2 N·m;采样周期为Ts=100µs. 传统三矢量MPCC的被控电机模型参数采用额定参数.ia,id,iq,ωr及快速傅里叶变换(fast Fourier transform,FFT)频谱的实验波形分别如图5(a)–5(e)所示. 图5 电机参数为额定值工况下三矢量模型预测电流控制实验波形Fig.5 Experimental waveform of three vector model predictive current control under rated motor parameters 为模拟实际的模型失配工况,这里设定模型转子磁链为额定值的1.3倍,模型定子电感为额定值的2倍,模型定子电阻为额定值的0.5倍.在模型失配工况下,ia,id,iq,ωr及FFT频谱的实验波形分别如图6(a)–6(e)所示. 图6 电机参数存在误差工况下三矢量模型预测电流控制实验波形Fig.6 Experimental waveform of three vector model predictive current control under the condition of motor parameter mismatch 将图5–6对比可见,当电机实际参数与模型参数出现较大偏差时,d,q轴电流波动有较大的增幅,a相电流畸变较明显,转速波动有小幅度变化. 在图5(e)中,相电流总谐波失真(total harmonic distortion,THD)值为1.62%;在图6(e)中,相电流THD值为10.41%,且较多谐波分量出现5 kHz附近. 在图6所示相同的失配工况下,图7给出了本文策略下的电机实验结果,并给出与电感扰动观测器[9]方法的比较.在电感扰动观测器方法中,包括电感干扰观测器和电感提取算法,可以实时更新整个控制系统的准确电感信息.该方法可以有效消除参数不匹配对控制性能的影响,降低MPCC方法的参数灵敏度. 图7 电机参数存在误差工况下自矫正的三矢量模型预测电流控制实验波形Fig.7 Experimental waveform of three vector model predictive current control based on self-correcting under the condition of motor parameter mismatch 本文策略下的ia,id,iq,ωr实验波形分别如图7(a)、7(c)、7(e)和7(g)所示,电感观测法的ia,id,iq,ωr实验波形分别如图7(b)、7(d)、7(f)和7(h)所示. 由图7可见,稳态时两种观测法对PMSM模型失配预测电流控制都有自矫正作用.相比于失配工况,矫正后的d,q轴电流波动明显减小,a相电流的畸变程度也有所改善. 为了更直观得反映a相电流的谐波含量,图8给出了两种方法的FFT频谱分析. 图8 a相电流FFT频谱分析对比Fig.8 FFT spectrum analysis of a phase current 图8(a)中,相电流THD值为3.77%;图8(b)中,相电流THD值为6.16%.图8(a)谐波分量集中在4∼5 kHz,但谐波含量相较图6(e)大幅度降低.而图8(b)谐波分量主要分布在0∼10 kHz. 定义d,q轴电流波动系数公式分别为式(50)–(51): 从图5–8中得到的d,q轴电流波动系数以及a相总谐波畸变率THD见表2. 表2 工况1的3种情况下电流纹波及THDTable 2 Current ripple and THD under three conditions of Condition 1 由表2可以看出,两种观测法均能有效减小失配工况下的电流波动系数及THD值.相比于电感观测法,内模控制观测法在模型失配工况下改善电流波形质量的效果更好. 工况2电机空载启动,给定转速为600 r/min;转速达到给定值后,负载转矩由0 N·m突增到6 N·m;采样周期为Ts=50µs. 传统三矢量MPCC的被控电机模型参数采用额定参数,ia,id,iq,ωr及FFT 频谱的实验波形分别如图9(a)–9(e)所示. 图9 电机参数为额定值工况下三矢量模型预测电流控制实验波形Fig.9 Experimental waveform of three vector model predictive current control under rated motor parameters 设模型转子磁链为额定值的1.3倍,模型定子电感为额定值的2倍,模型定子电阻为额定值的0.5 倍.在模型失配工况下,ia,id,iq,ωr及FFT频谱的实验波形分别如图10(a)–10(e)所示. 图10 电机参数存在误差工况下三矢量模型预测电流控制实验波形Fig.10 Experimental waveform of three vector model predictive current control under the condition of motor parameter mismatch 对比图9–10,并结合图5–6可见,当电机转速较小,负载转矩较大,实际参数与模型参数出现偏差时,三相电流波形谐波畸变程度明显升高,d,q轴电流波动有很明显的增幅.在图9(e)中,相电流THD值为0.30%;在图10(e)中,相电流THD值为11.78%,且较多谐波分量出现10 kHz附近. 在图10所示相同的失配工况下,图11给出了本文策略下的电机实验结果,并给出与电感扰动观测器方法的比较.其中,本文策略下的ia,id,iq,ωr实验波形分别如图11(a),11(c),11(e)和11(g)所示,电感观测法的ia,id,iq,ωr实验波形分别如图11(b),11(d),11(f)和11(h)所示. 图11 电机参数存在误差工况下自矫正的三矢量模型预测电流控制实验波形Fig.11 Experimental waveform of three vector model predictive current control based on self-correcting under the condition of motor parameter mismatch 由图11可见,两种方法在调速阶段下对电机模型失配预测电流控制仍有自矫正作用.相比于失配工况,矫正后的d,q轴电流波动明显减小,a相电流的畸变程度也有所改善.但内模控制观测法矫正后的d,q轴电流整体上要更光滑平整. 为了更直观得反映a相电流的谐波含量,图12给出了两种方法的FFT频谱分析. 图12 a相电流FFT频谱分析对比Fig.12 FFT spectrum analysis of a phase current 在图12(a)中,相电流THD值为0.31%;图12(b)中,相电流THD值为0.84%.图12(a)–12(b)谐波分量主要分布在10 kHz 内,且相电流THD 值都很接近图9(e).图12(a)谐波含量分布均匀且含量较少,而图12(b)在9∼10 kHz谐波含量较多.图12(a)中相电流谐波分量明显要优于图12(b). 从图9–12得到的d,q轴电流波动系数以及a相总谐波畸变率THD见表3. 表3 工况2的3种情况下电流纹波及THDTable 3 Current ripple and THD under three conditions of Condition 2 由表3可以看出,工况2因采样周期小,在正常工况和矫正工况下,电流波动系数和THD值都较小.两种观测法均大幅度减小失配工况下的电流波动系数及THD值,而内模控制观测法在改善电流波动系数和THD值方面都要优于电感观测法. 本文设计了一种基于IMC观测器的PMSM模型预测电流控制,其主要的贡献点和优点可概括为如下4个方面: 1) 从可行性来说,内模控制便于设计,易于实现,且在线计算量较小. 2) 从鲁棒性来说,基于IMC观测器的PMSM预测电流控制策略具有自矫正功能.在模型失配工况下,其能改善系统的电流波形质量,提高系统的鲁棒性. 3) 从实用性来说,基于IMC观测器的PMSM预测电流控制策略适用于不同工况.在高低速、稳态或调速阶段等不同工况,所提策略均表现出良好的控制效果. 4) 从控制性能来说,相比电感扰动观测器法,文中所提策略在改善电流波动系数和THD值都要优于前者,具有更好的控制性能. 文中所提基于IMC观测器的应对参数失配策略存在着参数估计精度问题,本文未深入研究参数估计误差的来源.通过分析参数估计产生误差的机理,结合智能算法提高参数估计精度将是下一步需要深入探讨的问题.2.5 价值函数选优
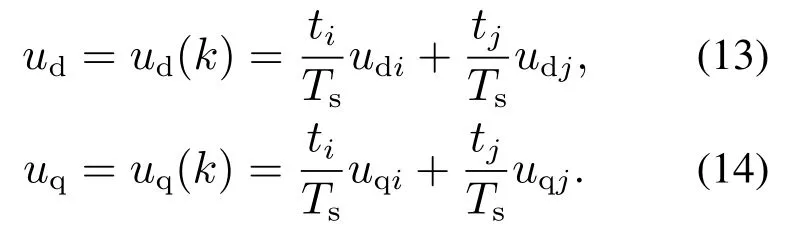
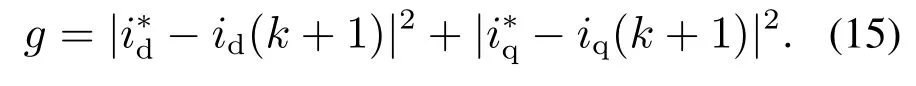
3 失配参数在线矫正的三矢量MPCC
3.1 IMC观测器设计

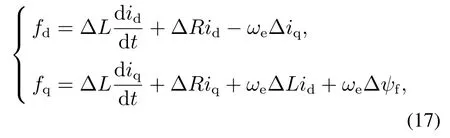
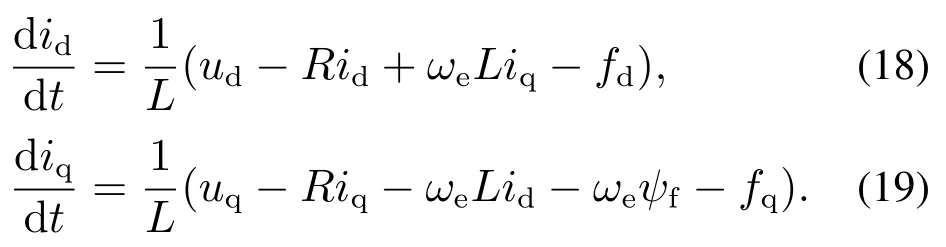



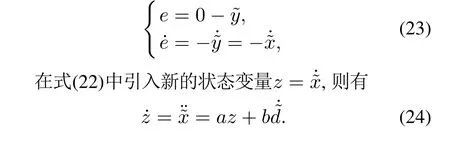



3.2 系统参数估计

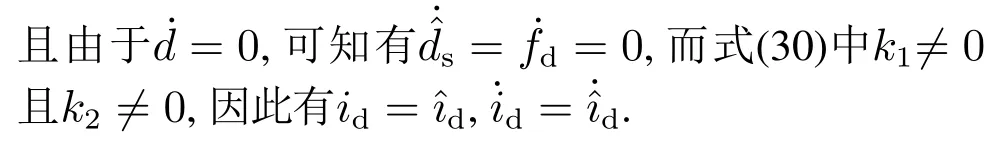


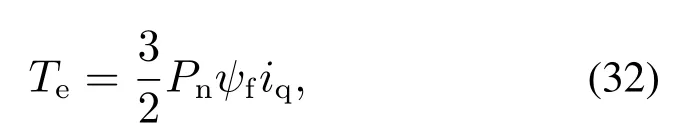


3.3 卡尔曼滤波系统




3.4 参数阈值化处理
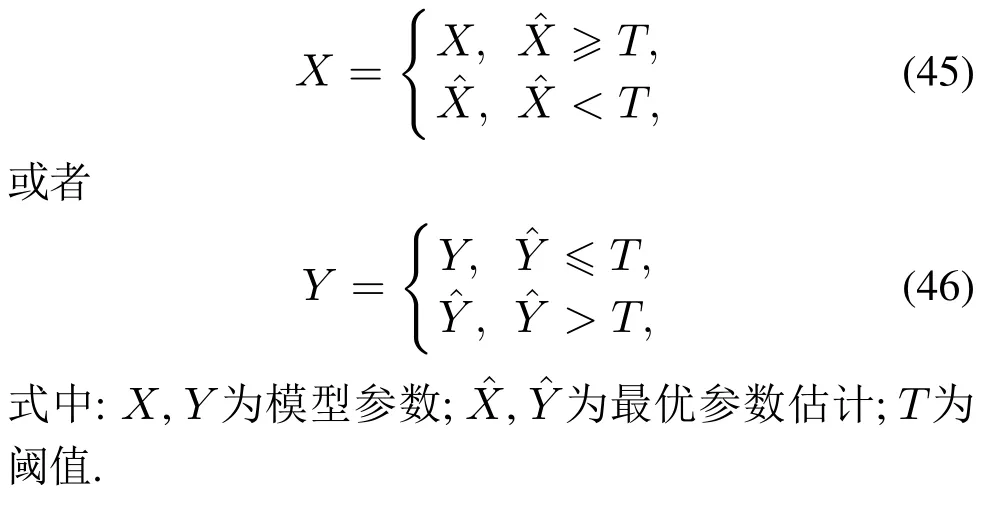

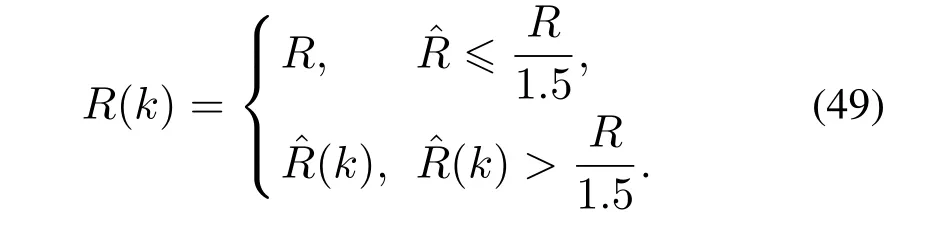
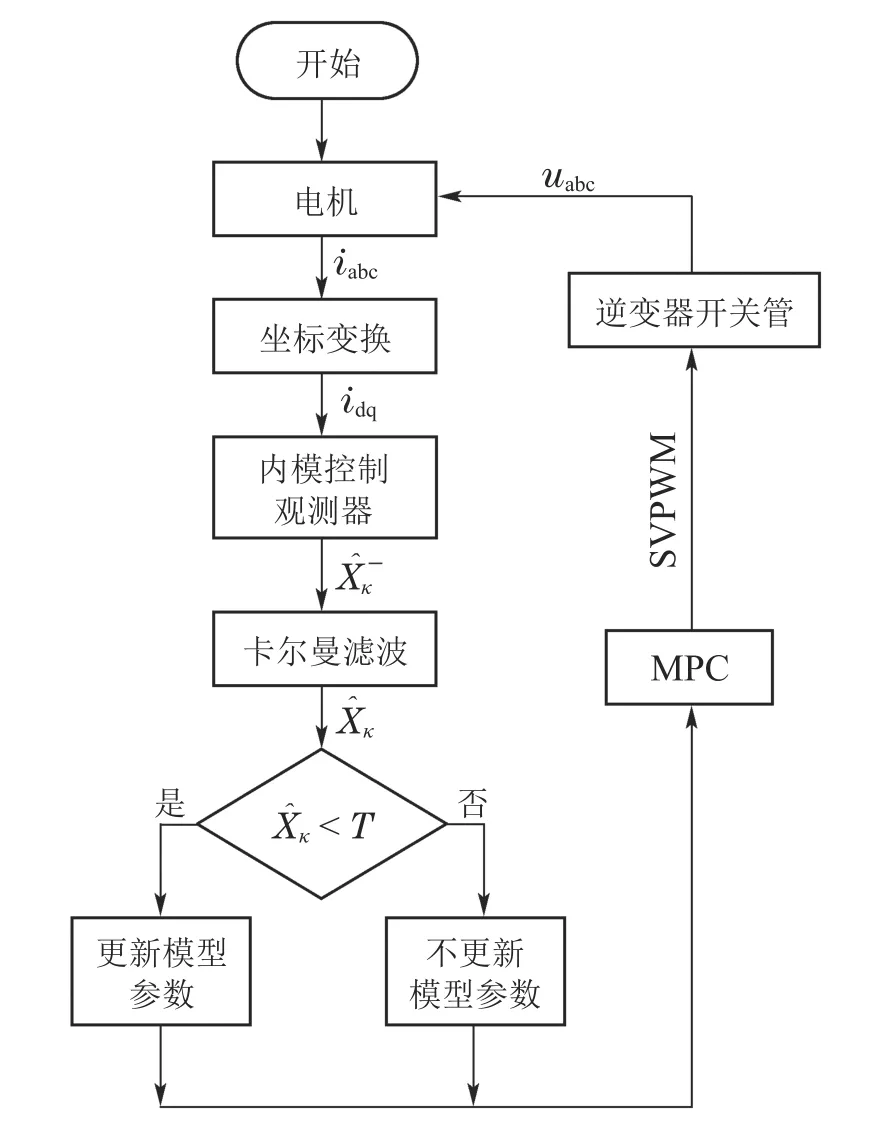
3.5 基于内模控制观测器应对模型失配策略
4 仿真实验



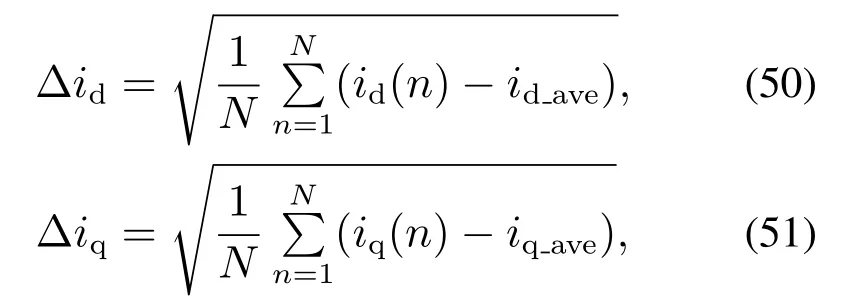


5 结论
