时速400km及以上高速铁路24～64m简支梁竖向频率限值

2021-06-18陈星宇徐昕宇周川江郑晓龙高芒芒

中国铁道科学 2021年3期

陈星宇，徐昕宇，周川江，郑晓龙，陈列，高芒芒

（1.中铁二院工程集团有限责任公司科学技术研究院，成都 610031；2.中国铁道科学研究院基础设施检测研究所，北京 100081）

为避免不均匀沉降造成的线路不平顺问题，高速铁路多架设在桥梁结构上，且以简支梁桥为主，如成达万高铁的桥梁占比约61%，京沪高铁的桥梁占比80.7%，沪杭高铁的桥梁占比高达92%。列车行经桥梁结构时会对其产生近似于固定频率的周期力作用。对于简支梁，由于梁端约束相对较弱，当车致动力作用的固有频率与简支梁桥的竖向固有频率相近时，则会出现明显的共振，可能导致桥梁毁坏并危及行车安全。针对不同跨度简支梁制定合理的竖向频率限值，使桥梁竖向固有频率避开车致共振频率区间，可以有效避免过大的梁体振动，保障桥梁安全和列车运行安全舒适。

松浦章夫等［1］基于多体动力学方法探究了铁路桥梁车致竖向共振问题，对比分析了轴距、轴重、定距、车长、车速等参数对车致共振的影响，研究表明车长和车速对车致动力作用的固有频率影响显著。国内学者开展的实测研究也得到同样结论［2］。Fryba［3］、夏禾［4］等均通过理论方法研究了车致桥梁共振的机理和共振发生车速。沈锐利［5］、宁晓骏［6］等于早期简要分析了高速简支梁桥竖向振动响应与跨度的关系。简方梁［7］、邓建良［8-9］等基于移动荷载列动力仿真分析，分别提出了城际铁路简支梁桥和磁浮轨道梁的竖向频率控制标准。李小珍［10］、宋晓东［11］、徐昕宇［12］等针对设计时速400 km 莫喀高铁常用跨度简支梁，采用CRH2型和CRH3型动车组的移动荷载模型，分析了简支箱梁的动力响应，提出了简支箱梁竖向频率限值。

我国已运营的高速铁路大大促进了部分区域的城市发展，更广阔范围的高速铁路建设仍处于高峰期。京沪线、沪杭线等高速铁路已实现350 km·h-1运行，成渝高铁的运行速度由350 km·h-1提升至380 km·h-1，成渝中线的设计时速为400 km，并预留80 km的提速空间，最高时速达到480 km。更高速度铁路是未来轨道交通发展的重要方向之一，对构建顺畅便捷的城市间的交通体系、实现区域经济协调发展，具有重大意义。但我国现行规范［13］涵盖的最高时速仅为350 km，现有关于高速铁路桥梁频率限值的研究也仅涉及40 m 以下跨度桥梁和400 km·h-1车速的列车。

本文针对更大跨度简支梁、更高运营速度、更新列车车型，开展简支梁竖向频率限值研究。以高速铁路24，32，40，48 和64 m 的简支箱梁为研究对象，建立CR400AF 型中国标准动车组的移动荷载列车模型，开展移动荷载列过桥的动力仿真计算，对比分析荷载列以140～520 km·h-1速度驶过不同竖向频率和不同跨度简支梁时桥梁跨中的动力响应，研究桥梁参数对梁体动力响应的影响规律，以设计荷载的动力作用大于列车荷载的动力作用为原则，并结合规范要求，明确时速400 km及以上高速铁路更大跨度区间简支梁的竖向频率限值。

1 车-桥系统模型

1.1 分析模型

已有研究表明［5，8］，探究桥梁结构在列车荷载作用下的动力响应时，可将列车模型简化为移动荷载列，与车-桥耦合模型的动力响应相比，2 种分析模型的桥梁动力响应特征基本吻合。简支梁竖向频率限值研究中需要针对不同跨度、不同频率、不同车速进行大量的计算分析，综合精度需求和计算效率，移动荷载列模型更简便易行。

根据列车轴重和轴距等车辆参数，采用多体动力学软件SIMPACK，通过施加分布集中力，建立移动荷载列模型，实现列车动力作用模拟。在有限元软件ANSYS 中，通过梁单元模拟简支梁，建立桥梁有限元模型。在SIMPACK软件中组合移动荷载列模型与桥梁有限元模型，建立移动荷载列车-桥梁系统模型，其中列车采用16 节编组形式，桥梁模型为10跨简支梁，模型示意图如图1所示。

图1 车-桥系统模型示意图

1.2 车辆参数

为满足国内列车更高速度的需求，我国自主研发的复兴号CR400AF 系列中国标准动车组应运而生，该车型持续运营速度达400 km·h-1，样车的设计最高速度达430 km·h-1。

对于时速400 km 以上高速铁路简支梁，针对性地选用CR400AF 型动车组作为其上部活载，列车模型示意如图2所示。车辆轴距为2.5 m，转向架中心距为17.8 m，车钩中心距为25.65 m，拖车的轴重为118.2 kN，动车的轴重为131.03 kN。

图2 CR400AF型动车组参数（单位：m）

1.3 桥梁参数

参考高速铁路简支梁工程实例，结合既有桥梁设计经验，初拟各跨度简支梁的梁体参数，其中24，32 和40 m 简支梁采用C50 混凝土，梁体横断面如图3所示，图中H为梁高；而48 和64 m 简支梁采用更高强度的C60 混凝土，其横断面如图4所示。桥梁二期恒载均按160 kN·m-1考虑。

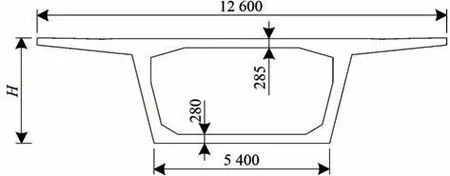
图3 24，32和40 m简支箱梁横断面图（单位：mm）

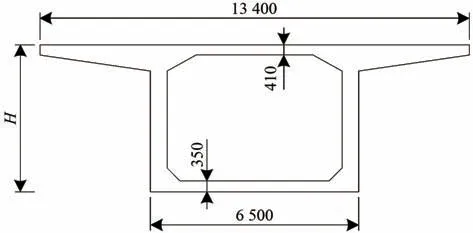
图4 48和64 m简支箱梁横断面图（单位：mm）

针对不同竖向频率的简支箱梁结构，对箱梁截面进行适当简化，即保持顶、底板厚度和宽度均不变，通过调节箱梁的空箱高度改变箱梁整体高度，进而改变梁体的刚度，最终达到改变简支梁自振频率的目的。本文确定各跨度简支梁频率研究范围的原则为：在满足构造要求的情况下，使简支箱梁的空箱高度取值尽可能小，此时的梁体竖向频率即为研究范围的下限值；在箱梁初设尺寸的基础上增大1 倍梁高，此时的梁体竖向频率即为研究范围的上限值；在频率研究范围内，频率间隔为0.5 Hz。根据该方法建立的各跨度简支梁截面高度与竖向频率的对应关系见表1。

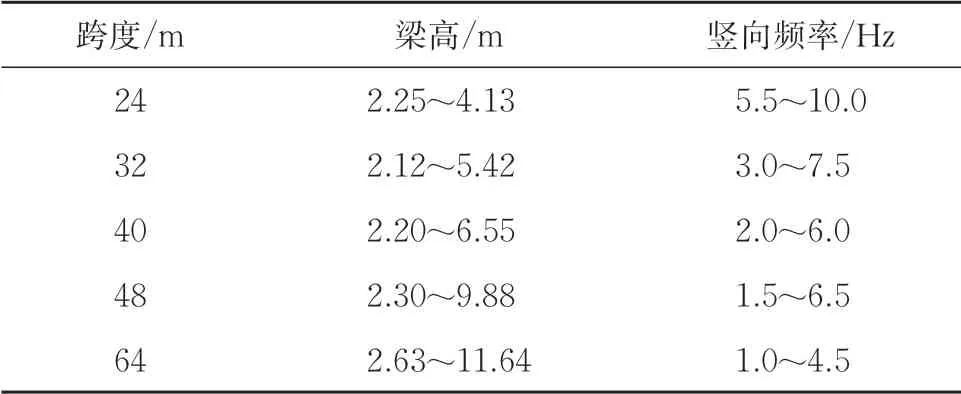
表1 各跨度简支梁截面高度与竖向频率对应表

根据主梁断面尺寸，采用有限元方法，针对不同跨度、不同尺寸的简支梁，建立相应的10 跨简支梁有限元模型。

2 竖向频率限值评判标准

我国规范［13］规定，在桥梁设计中通过设计荷载乘以动力系数（1+μ）考虑列车活载的动力作用，设计荷载通常选用ZK 活载。为了体现列车对桥梁产生的近似于固定频率的周期性动力作用，采用实际列车简化的移动荷载列模型。根据既有研究的相关结论［5，10，11］，下文研究中以考察设计荷载的动力作用是否大于实际列车荷载的动力作用作为竖向频率限值的评判标准，如式（1）所示。若设计荷载的动力作用大于实际列车荷载的动力作用，表明桥梁设计时充分考虑了活载动力作用，桥梁竖向频率满足要求。

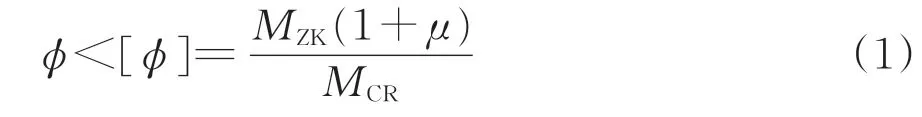
其中，

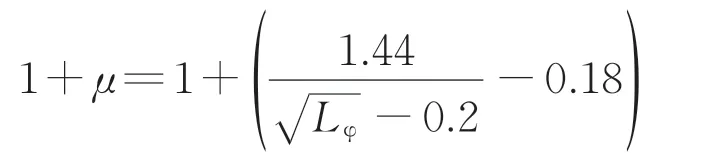
式中：ϕ和[ϕ]分别为CR400AF 型动车组荷载作用下桥梁结构的动力系数和容许动力系数；MZK和MCR分别为ZK活载和CR400AF型动车组荷载作用下简支桥梁跨中静弯矩；Lφ为简支梁的跨度。

表2 为各跨度简支梁的容许动力系数。可见，在24～64 m 跨度范围内，简支梁的容许动力系数随着跨度的增大呈现先增大后减小的趋势，其中24 m 简支梁的容许动力系数最小，40 m 简支梁的容许动力系数最大。

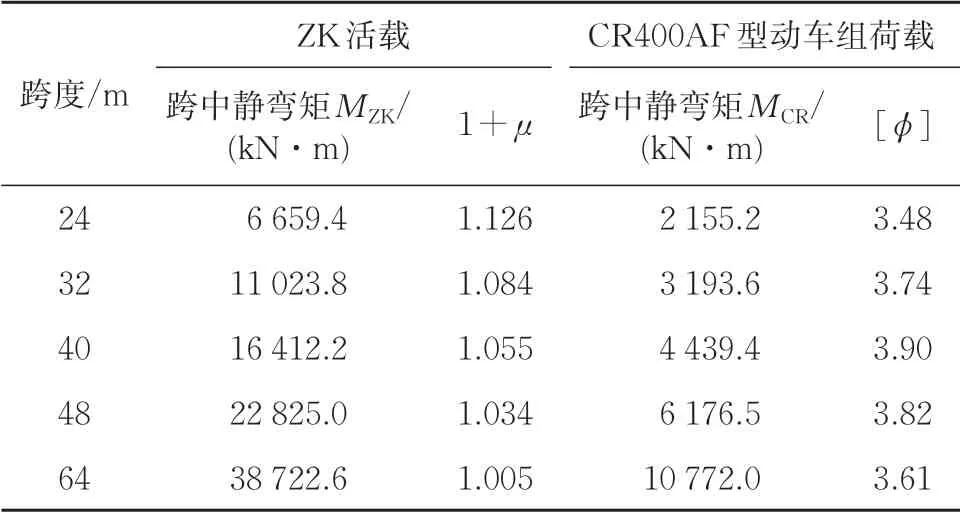
表2 各跨度简支梁容许动力系数

3 梁体动力响应影响因素

3.1 跨度对梁体动力响应的影响

为探究简支梁跨度对梁体动力响应的影响规律，在140～520 km·h-1范围内，进行竖向频率相同但跨度不同的简支梁的动力响应分析。

由于5 种跨度简支梁的频率研究范围未出现重合，图5 仅给出32，40，48 和64 m 共4 种跨度的简支梁在3.5 Hz 频率时的动力响应，图6 给出了24，32，40 和48 m 共4 种跨度简支梁在5.5 Hz 频率时的动力响应。

由图5和图6可知，当行车速度处于某特定速度区间时，桥梁结构的动力响应将显著增大，且在某一确定速度下达到最大，对于竖向频率为3.5和5.5 Hz的简支梁，该速度分别为320和520 km·h-1，与共振车速的理论计算结果相近。

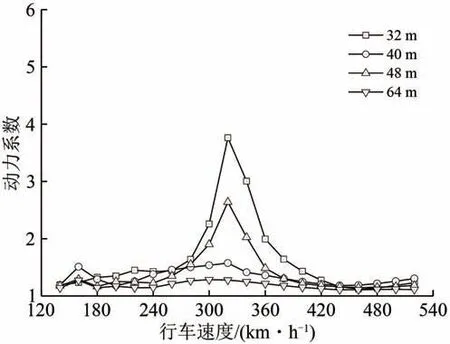
图5 频率为3.5 Hz时不同跨度简支梁动力响应

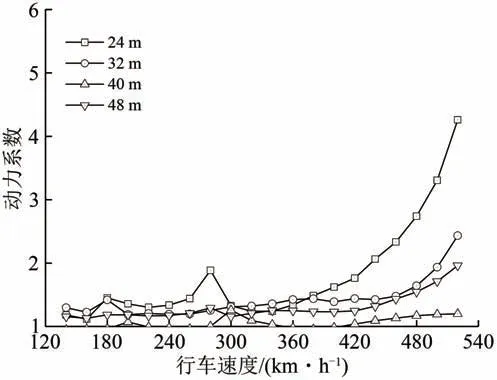
图6 频率为5.5 Hz时不同跨度简支梁动力响应

在140～520 km·h-1行车速度范围内，24 和32 m 简支梁均出现了超谐共振，简支梁高阶超谐共振时梁体的动力响应远小于1 阶共振车速下梁体的响应。

梁体动力响应总体随着跨度的增大而减小，其中64 m 跨度简支梁的动力响应最小，40 m 简支梁的动力响应也明显小于32 和48 m 简支梁。这是因为简支梁跨度为车长的0.5+i倍（i=1，2，…）时，消振作用尤为突出，此时共振现象消失［10］，当简支梁跨度为40 和64 m 时，跨度与车长之比分别为1.56 倍和2.50 倍，车致桥梁共振被不同程度地抑制。

3.2 频率对梁体动力响应的影响

为探究简支梁竖向频率对梁体动力响应的影响规律，在140～520 km·h-1行车速度范围内，进行跨度相同但竖向频率不同的简支梁的动力响应分析。

图7和图8分别给出了32 和64 m 简支梁在6种和4种不同竖向频率下的梁体动力系数。

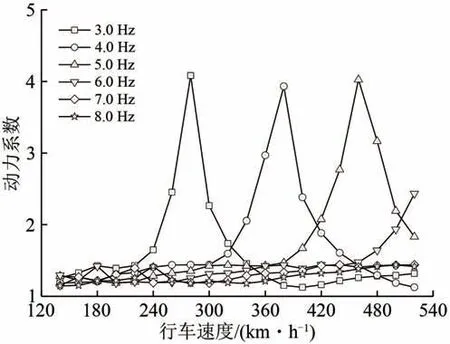
图7 32 m简支梁在不同频率时的动力响应

由图7可见，对于32 m简支梁，随着竖向频率的增大，梁体动力系数峰值对应的行车速度逐渐增大；当竖向频率超过6.0 Hz时，梁体共振车速已超过520 km·h-1，此时520 km·h-1以下速度区间内的梁体动力系数峰值显著减小；当竖向频率在5.0 Hz 及以下时，梁体的动力系数最大值相近，约为4.0；当竖向频率在7.0 Hz 及以上时，梁体的动力系数最大值相近，约为1.5；竖向频率在5.0～7.0 Hz范围内时，梁体的动力系数峰值变化显著。究其原因，通过理论分析可知，共振车速为520 km·h-1所对应的竖向频率为5.6 Hz，当梁体竖向频率超过该频率一定范围后，在140～520 km·h-1行车速度范围内简支梁将不发生1阶车致共振。

由图8 可知，对于64 m 简支梁，在140～520 km·h-1行车速度范围内，当频率为1.0 和2.0 Hz时，梁体动力系数总体随车速的增大而增大；当频率为3.0和4.0 Hz时，梁体动力响应在一定速度达到最大，但此时动力响应增大幅度在1.2 倍以内，且该速度并非理论计算的共振车速。

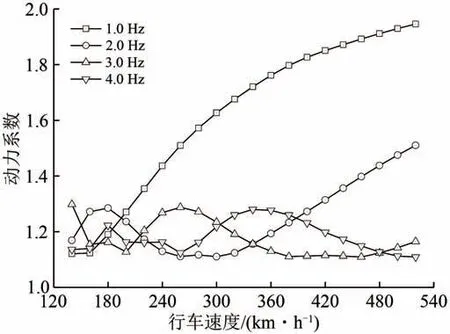
图8 64 m简支梁在不同频率时的动力响应

4 竖向频率限值

4.1 梁体最大动力响应

图9 给出了在140～520 km·h-1行车速度范围内，不同跨度、不同竖向频率简支梁的最大动力系数。图中黑色实心图标表示在520 km·h-1车速范围内，对应简支梁的最大动力系数不满足容许动力系数的要求。

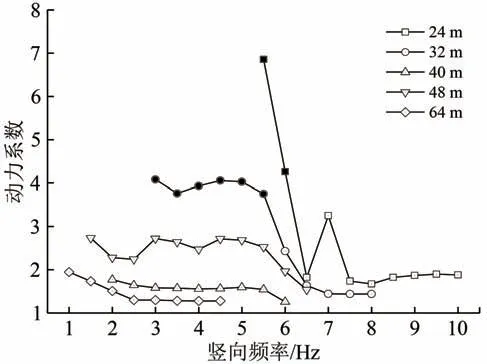
图9 不同跨度、不同竖向频率简支梁最大动力响应

由图9 可见，对于48 m 及以下跨度的简支梁，竖向频率在5～7 Hz 范围内时，最大动力系数随着竖向频率的增大而降低，变化幅度随着跨度的增大而减小。

由图9 还可见：当24 m 简支梁的竖向频率在6.5 Hz 及以下，及32 m 简支梁的竖向频率在6.0 Hz 及以下时，梁体动力响应过大；48 m 简支梁的最大动力系数均小于3.0，40 和64 m 简支梁的最大动力系数均在2.0 以内，均满足容许动力系数要求。

对于任意跨度的简支梁，通过控制其竖向频率，使其达到一定标准后，都能够使该简支梁结构在520 km·h-1及以下车速范围内的梁体动力响应满足要求。

4.2 竖向频率限值

根据现行《高速铁路设计规范》［13］规定，对20 m ＜Lφ≤96 m 的简支梁，其竖向自振频率下限值为23.58L-0.592φ，经计算得到各跨度简支梁竖向频率限值见表3。

表3 依据规范得到的简支梁竖向自振频率限值

根据移动荷载列过桥的计算分析结果，基于设计荷载的动力作用大于列车荷载的动力作用的原则，考虑最大检算速度为运营速度的1.2 倍，得到满足动力系数要求的频率限值，结合表3 中的规定，确定不同速度条件下5种跨度简支梁梁体竖向频率限值，结果见表4。

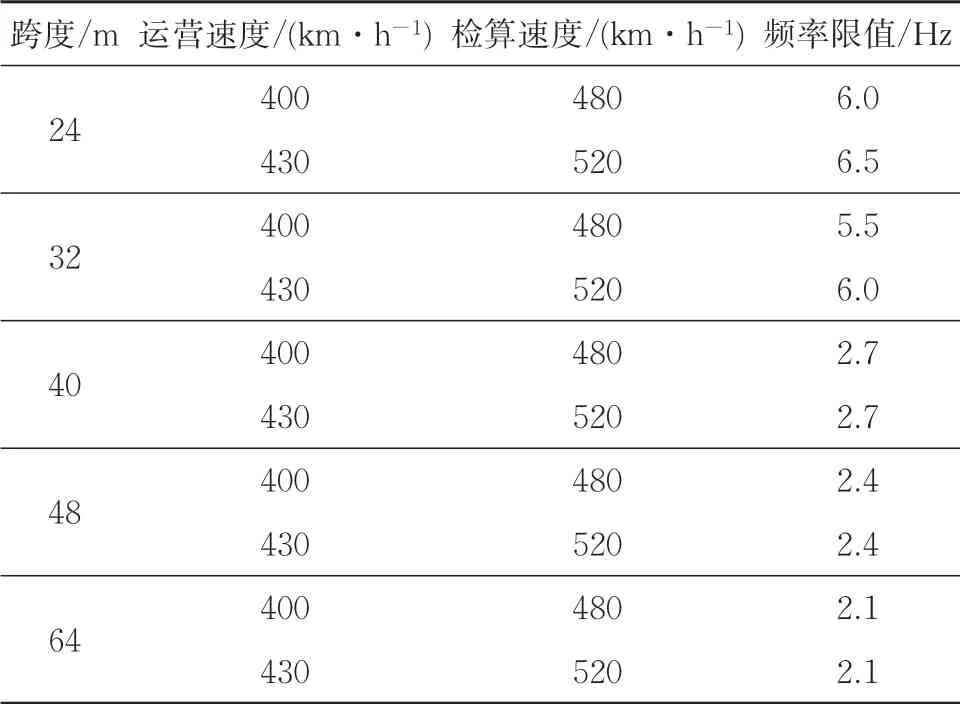
表4 各跨度简支梁竖向频率限值

由表4 可知：频率限值的要求随着简支梁跨度的增大而减小，32 m及以下跨度简支梁的频率限值远高于40 m 及以上跨度简支梁。将CR400AF 型动车组的运营速度由400 km·h-1提至430 km·h-1，24 和32 m 简支梁竖向频率限值需要提高0.5 Hz，而40 m及以上跨度简支梁竖向频率限值保持不变。

对于24 和32 m 简支梁，与基于CRH2，CRH3等车型动车组确定简支梁频率限值相比［10-12］，由于车长和轴重的不同，运营速度达400 km·h-1的CR400AF 型动车组对梁体频率限值的要求提高约15%。