压装车轴镶入部裂纹缺陷信息提取

武冬冬，杨 凯，彭朝勇

（1.成都主导软件技术有限公司技术中心，四川成都 610091；2.西南交通大学物理科学与技术学院，四川成都 610031）

在役轨道车辆车轴达到一定的检修修程时，须进行车轴的超声波无损探伤，以保障车辆运行安全。装配轮对时车轮与车轴镶入部间的过盈配合，使得车轴镶入部存在应力集中区［1］。车辆在日常运行过程中车轴承受持续的轮轴间相互作用力［2］和交变应力等共同作用，使得压装车轴镶入部成为疲劳裂纹缺陷高发区［3］，进而可能产生车轴断裂的风险［4］。

随着超声波检测技术的发展，对车轴的探伤也由早期的人工手持常规超声波探头探伤，逐步优化为基于相控阵超声波检测技术的自动化探伤［5］，这改变了人工常规超声波探伤扫查范围小、效率低、耦合不稳定等现象，实现具有多角度、大范围、多点聚焦等功能的自动化电子扫查，提高了检测效率、扫查范围、缺陷检测能力和稳定性［6］。但是，由于轮对的轮轴接触界面［7］存在应力集中及一定的粗糙度和微动腐蚀，使用常规超声波或相控阵超声波检测技术对压装车轴镶入部进行检测时，超声检测回波中都含有较强的在轮轴接触界面处产生的噪声，当缺陷回波幅值与噪声回波幅值接近，甚至低于噪声回波幅值时，很容易造成缺陷漏判。同时，现有对于压装车轴镶入部超声波检测波形的优化算法［8］，需要以缺陷回波幅值高于噪声回波幅值为前提，基于检测结果成像为优化对象进行噪声消除［9］，以提高检测成像质量和缺陷检出信噪比，但有削弱缺陷回波幅值的可能。

本文针对超声波检测结果中噪声信号幅值较大，缺陷信号被淹没在噪声信号中、无法直接识别的状况，在进行超声波检测信号特征分析的基础上，采用小波包变换对检测信号进行局部化时频域分析，提取缺陷特征系数和缺陷幅值系数，再将重建后的波形作为判别车轴镶入部的超声波检测信号中是否存在疲劳裂纹缺陷的依据。

1 检测信号数据采集及特征

使用由相控阵超声波探头（工作频率为5 MHz、晶片为32 个、晶片总体尺寸为20.0 mm×19.2 mm）、相控阵超声波采集仪器（采集频率为100 MHz）、数据分析主机组成的超声检测平台，分别对镶入部含缺陷和无缺陷的压装车轴进行超声波检测信号数据采集。

采集检测信号时，相控阵超声波探头与车轴端面稳定耦合，并使不同角度的超声波声束覆盖车轴镶入部。其中，镶入部裂纹缺陷是按照压装车轴镶入部自然疲劳裂纹缺陷［10］形态加工而成的不同深度的横向裂纹缺陷，分布在镶入部的不同位置，裂纹缺陷深度有0.5，1.0 和1.5 mm 这3 种，裂纹宽度均为0.2 mm。车轴镶入部裂纹缺陷制作完成后，车轴与车轮按照铁总运［2013］191 号《铁路客车轮轴组装检修及管理规则》中的“组装要求”进行过盈压装，组装成样板轮对。检测平台信号获取及裂纹缺陷的分布和形态如图1所示。

图1 检测平台信号获取及裂纹缺陷的分布和形态示意

采集得到的车轴镶入部超声波检测典型检测信号如图2所示。

图2 压装车轴镶入部3种典型超声波检测信号

从图2 可以看出：无裂纹缺陷时，信号波形只含有噪声信号；缺陷信号分为2 个类型，一类是缺陷信号未被噪声信号淹没，信号波形中缺陷信号幅值明显高于噪声信号幅值，该缺陷信号具有较高的信噪比，较易识别，另一类是缺陷信号被噪声信号淹没，缺陷信号幅值与淹没其的噪声信号幅值基本相当，在识别时会被当作噪声信号，即信号波形被误认为只含有噪声信号而不含有缺陷信号，造成裂纹缺陷漏检。

2 信号小波包变换

在传统的平稳信号分析和处理中，基于傅里叶变换的信号频域分析发挥了极其重要的作用，但由于其为基于信号全部时域信息的整体变换，对于非平稳信号不具有时间和频率的定位功能，只能给出信号变换后的总体效果，而不能展示信号在某一时刻的本质特征。小波变换和小波包变换都具有时频域分析功能，小波变换只能对信号的低频部分做进一步分解，而小波包变换［11］同时还能对信号的高频部分做进一步分解，可实现对分解信号进行全面的时频域局部化分析。

基于超声检测信号的特征分析，使用Coiflets小波函数对压装车轴镶入部信噪比为6 dB 以上未被噪声信号淹没的缺陷信号和无裂纹缺陷的噪声信号进行4 层小波包分解，通过规律性提取含有缺陷信息的缺陷特征系数和缺陷幅值系数。信号进行小波包分解后，15 和17 小波包节点组成缺陷特征系数，含有缺陷信号和较少量噪声信号；16 和18 小波包节点组成缺陷幅值系数，含有幅值较高的缺陷信号和一定量的噪声信号。基于2 组系数的重建信号波形分别如图3和图4所示。

从图3 和图4 可以看出：重建后信号波形均能体现缺陷信号和噪声信号的明显特征，即未被噪声信号淹没的缺陷信号具有较高的信噪比，噪声信号无收敛性或相对高幅值特征。

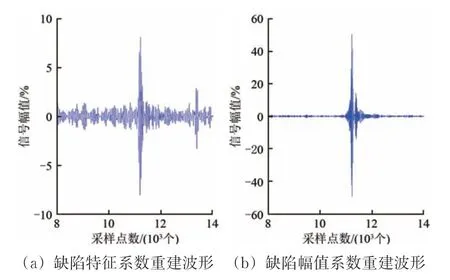
图3 未被噪声信号淹没的缺陷信号小波包变换波形

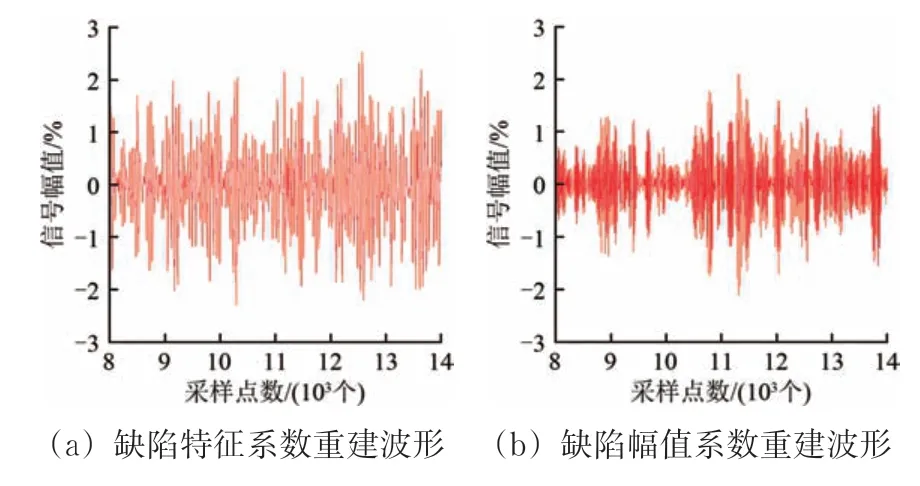
图4 噪声信号小波包变换波形

对缺陷信号被噪声信号淹没的检测信号进行小包波变换分解，提取2 组系数并重建信号波形，结果如图5所示。从图5 可以看出：尽管缺陷信号被噪声信号淹没，但基于2 组系数的重建波形均体现了缺陷信号的明显特征，可以用来辨别车轴镶入部是否存在缺陷，避免缺陷信号被当作无缺陷时噪声信号。

尽管通过小波包变换可提取淹没在噪声信号中缺陷信号的主要缺陷成分，可是由于噪声分量的存在，使缺陷成分表现的缺陷信息不够清晰（如图6（a）所示）。使用基于logistic函数［12］的自寻优阈值滤波算法［13］，对重建后的信号波形进行滤波，可以得到较为清晰的高信噪比缺陷分量（如图6（b）所示）。

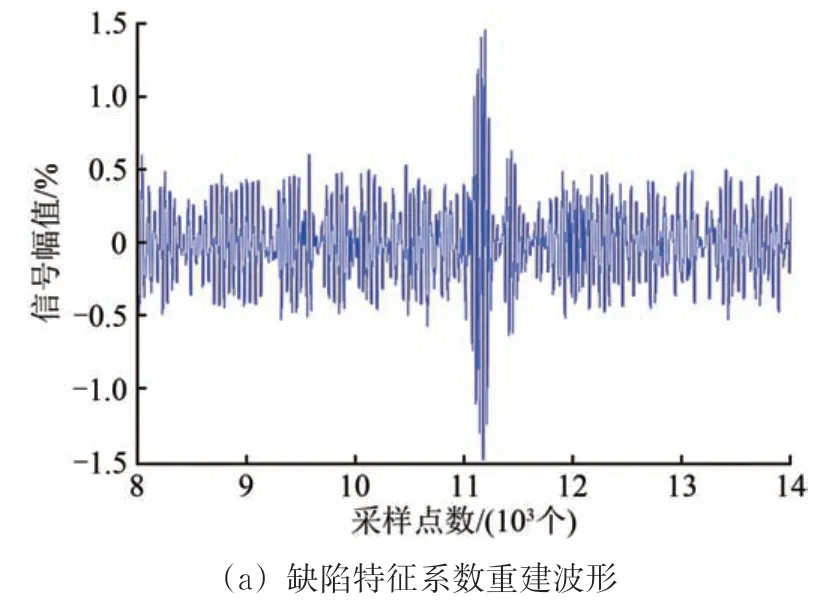
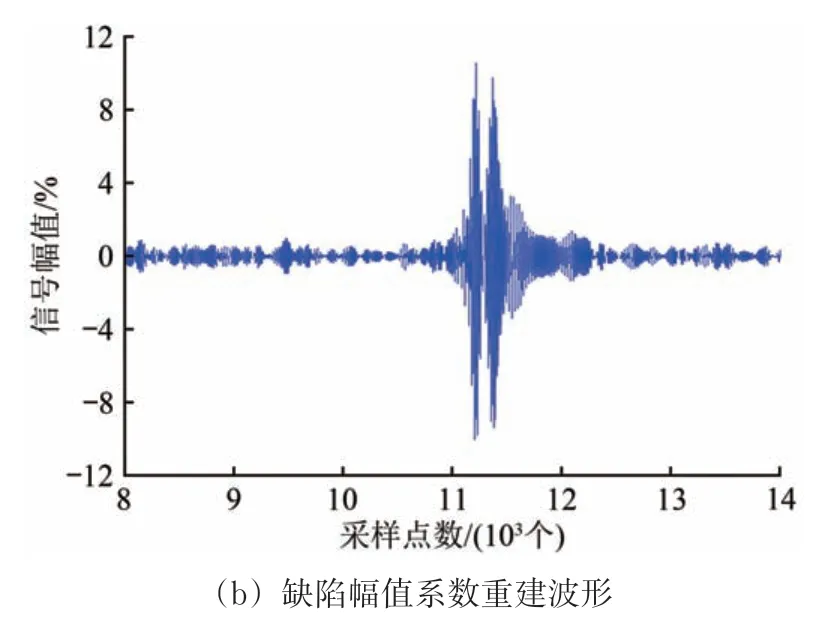
图5 被噪声信号淹没缺陷信号小波包变换波形

图6 缺陷信号淹没在噪声信号时重建波形滤波前后对比

滤波阈值sn为

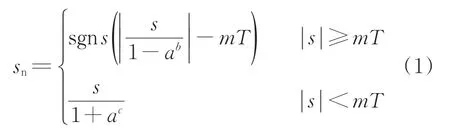
式中：s为原始信号；T为阈值；m为阈值T的调节参数；a，b，c为logistic函数的通用参数。

通过调节参数a，b和c，可优化logistic函数形成的“S”形曲线的梯度，以抑制噪声信号幅值并保留缺陷信号幅值，提升缺陷信号信噪比。

采用该滤波算法对噪声信号重建波形的滤波前后对比如图7所示。从图7 可以看出：滤波对噪声信号幅值有削弱作用。

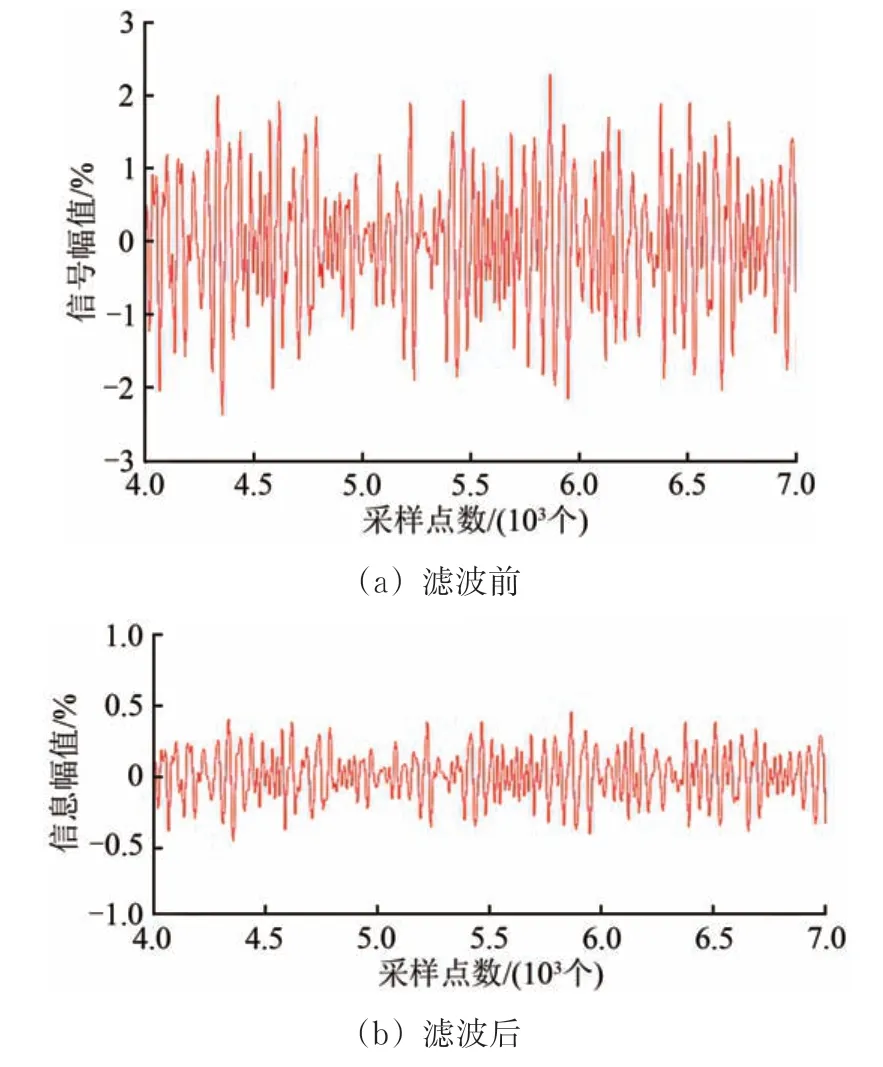
图7 噪声信号重建波形滤波前后对比

3 算例验证

为验证基于缺陷特征系数和缺陷幅值系数重建后的信号波形是否可以辨别出车轴镶入部存在的疲劳缺陷，先收集样板轮对车轴镶入部超声波检测信号中的缺陷样本和无缺陷样本，作为训练数据，并搭建神经网络［14］，再基于预测数据，对未知样本进行预测，判断其中是否含有缺陷信息。基于神经网络的预测流程如图8所示。

图8 基于神经网络预测流程

训练数据中，缺陷样本共32组，信噪比为6 dB以上（见图2（b）和图9（a）），设定缺陷样本的训练目标值为数值9。无缺陷样本共42组，其中4组取自样板轮对车轴镶入部超声波检测信号（见图2（a）），其余38组取自达到一定运行里程和新压装未运行的车辆段现场无缺陷轮对车轴镶入部超声波检测信号（见图9（b）），并设定无缺陷样板的训练目标值为数值0。

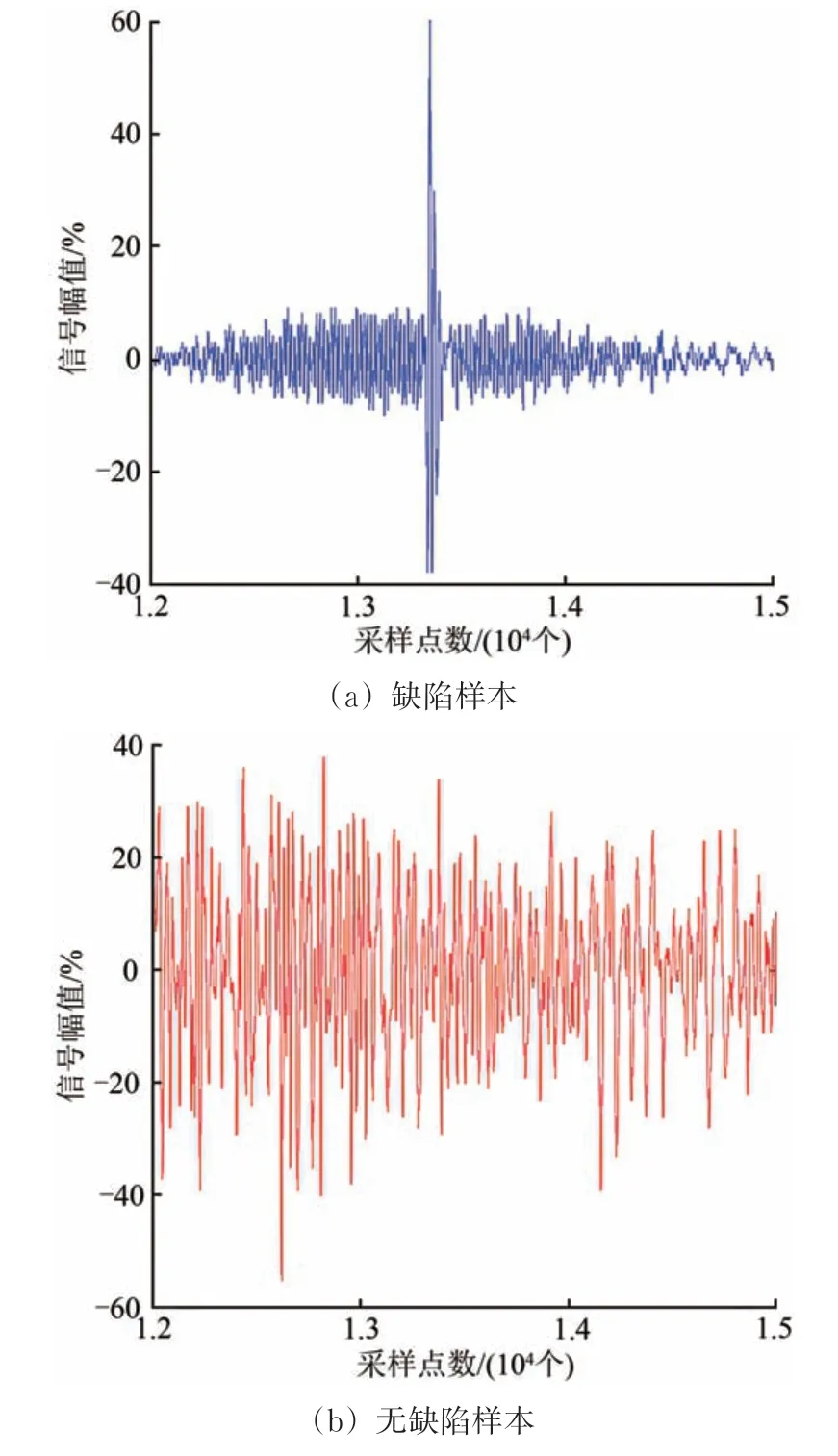
图9 典型训练数据

使用非线性最小二乘算法，列文伯格-马夸尔特法（Levenberg-Marquardt）进行网络训练，在这74 组训练数据中，算法随机取其中52 组样本作为网络训练输入，11 组样本作为网络泛化优化，其余11 组样本用于网络性能的独立测试。当网络输出值与目标值的均方误差为5.2×10-9时泛化优化停止、训练完成，神经网络搭建完毕。

训练数据范围外的预测数据共10组，其中前6组数据取自缺陷信号淹没在噪声信号中的超声波检测信号（见图10（a）），后4组数据取自只含有噪声信号的超声波检测信号（见图10（b））。

从图10 可以看出：预测数据中缺陷样本具有缺陷信号被淹没在噪声信号时的典型特征。

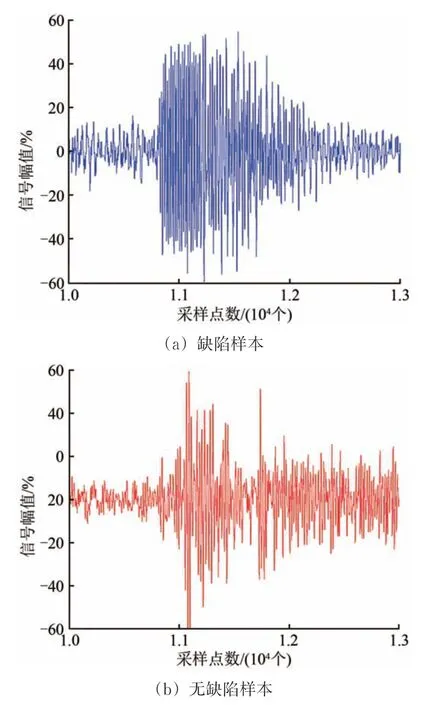
图10 典型预测数据

基于神经网络的预测结果见表1。从表1 可以看出，采用本文方法识别正确率达100%。表明缺陷信号被淹没在噪声信号时，采用传统的识别方法，缺陷易被漏判，但经采用本文所述方法，缺陷可被识别。

表1 基于神经网络预测结果

4 结论

（1）利用小波包变换在时频域对信号分解的高分辨特性，提取用于区别噪声信号的缺陷特征系数和缺陷幅值系数，基于这2 组系数的重建波形含有缺陷的主要信息。

（2）通过对缺陷特征系数和缺陷幅值系数的重建，可以从噪声信号中恢复出缺陷信号的主要信息，并使用基于logistic 函数的自寻优阈值滤波改进算法，提高缺陷信号信噪比。

（3）收集标准压装的样本轮对车轴镶入部和车辆段现场轮对车轴镶入部的缺陷信号和噪声信号，作为神经网络的训练样本的原始数据，使用搭建好的神经网络对样本范围以外的缺陷信号和噪声信号进行预测，预测结果与目标值一致，证明使用基于缺陷特征系数和缺陷幅值系数的重建信号波形可以有效区分缺陷信号和噪声信号。