金属Nb的Finnis-Sinclair势开发及势函数形式对材料性能的影响*

2021-06-18高静怡孙嘉兴王逊周刚王皞刘艳侠徐东生

物理学报 2021年11期

高静怡孙嘉兴王逊周刚王皞刘艳侠† 徐东生

1) (辽宁大学物理学院，沈阳 110036)

2) (沈阳建筑大学理学院，沈阳 110168)

3) (中国科学院金属研究所，沈阳 110016)

对于计算材料科学的研究者来说，经常由于找不到合适的原子间势而工作受阻.本文将在Finnis-Sinclair势的框架下，通过开发金属Nb的Finnis-Sinclair势而给出较详细的原子间势拟合、检验、修正的过程.首先建立原子间势与材料宏观性能之间的关系，然后通过再现金属Nb的结合能、体模量、表面能、空位形成能及平衡点阵常数的实验数据的方法拟合金属Nb的Finnis-Sinclair势.利用所构建的原子间势计算金属Nb的弹性常数、剪切模量及柯西压力来检验势函数.讨论势函数曲线形状对间隙形成能的影响，进而根据间隙能的计算数据修正已构建的原子间势.讨论截断距离的处理方法.本文的结果一方面为构建原子间势函数库提供资料，为构建与Nb相关的合金原子间势奠定基础; 另一方面，为开发和改善原子间势质量提供方法和依据.

1 引言

原子尺度模拟是微观层次研究材料性能行之有效的手段和途径，但是计算机模拟结果的可靠性直接来源于原子间势的质量[1]，而且模拟的计算量强烈依赖于原子间势的复杂度.因此开发形式简单、质量可靠的原子间势及建立易于操作的原子间势构建方法极为重要.目前，原子间势的开发大多通过有限的势函数参数来再现材料的部分性质而获得[2-4]，因此，根据部分性能获得的原子间势不可能描述材料的全部性能.由于研究目的不同，有时即使是同一金属[5-10]或合金[11，12]也需要开发不同的原子间势.

Nb基合金及含Nb合金在航空航天、医学、核工业等领域有着重要的应用[13-15].为了从原子尺度研究Nb及其合金的性能，首先需要构建其原子间势.在金属及合金中应用广泛的原子间势模型主要是1983—1984年间由Daw和Baskes[16，17]提出的Embedded-atom method (EAM)势模型，以及1984年由Finnis和 Sinclair[2]提出的Finnis-Sinclair (FS)势.二者数学表达式都由两项组成，第一项都为排斥势，解释相同，都是原子芯之间的静电势; 第二项都为吸引势.二者的主要区别在于第二项，体现在两个方面: 一是来源不同， EAM势来源于密度泛函理论， FS势来源于紧束缚理论的二阶矩近似; 二是对第二项即电荷密度函数和嵌入能函数的解释不同， EAM势中，把金属中的每个原子看成是镶嵌在其他原子在该位置形成的电子气中的一个杂质，并假设嵌入能是局域电子密度及其高阶导数的函数，且电子密度由原子的电荷密度叠加而成; 而FS势中，每个原子内聚能的大小与原子间最近邻的键合数的平方成正比，在紧束缚理论中，金属中电子能带的带能是其中占据态单电子能之和，而且带能由态密度的二阶矩来表征，因此密度函数是态密度的二阶矩.虽然这两种原子间势的来源和解释不同，但由于二者的数学形式相近，为此，人们习惯上将FS势归入为EAM模型.本文为了叙述上的方便，仍然称作FS势.到目前为止，在金属及合金中广泛使用的原子间势形式依然是EAM势及FS势，以及对这两种势的各种修正势[18-20].

1984年Finnis和 Sinclair[2]开发了7种bcc结构金属Nb， V， Ta， Cr， Mo， W及Fe的FS势，首次考虑了原子之间的多体效应，克服了对势的缺点.但该势的缺点是在近距离下原子之间的排斥力不足，特别是V和Nb，在短距离内甚至表现出有吸引力，导致分子动力学模拟时出现原子落在一起的异常行为[21].为此， Ackland[21]和Rebonato[22]分别对该问题进行了修正，对于小于第一近邻的对势曲线进行了硬化.另一方面，该势的原子间相互作用距离考虑到第二近邻，相互作用距离比较短.本文在该势的基础上，首先，扩展相互作用距离到第三近邻，并修正近距离相互作用偏软的现象; 其次，建立原子间势与材料宏观性质之间的关系，讨论函数形式及截断距离对宏观性能的影响，并根据材料的宏观性质修正原子间势函数形式.

构建原子间势是一项复杂的工程，本文将从模型的选择，截断距离处理，势函数拟合，势函数检验及应用，以及根据检验和应用结果修正势函数几方面详细介绍势函数的开发过程，并就截断距离和势函数形式对原子间势的质量及材料性能影响方面进行了讨论，期望为开发和改善原子间势质量提供参考.

2 模型

本文在FS势框架下[2]开发金属Nb的原子间势，将原子间相互作用扩展到第三近邻.对于理想单质金属，所有原子都是等价的，因此体系的总能可以表示为单原子能量之和，单个原子的相互作用能表示为:

其中，uP表示原子对之间的相互作用能，uN表示多体相互作用对总能的贡献.它们可用(2)式和(3)式表示:

其中，A为势参数，是大于零的常数.根据紧束缚理论，取ρ为参考原子i处的局域电子密度，表示如下:

其中，φ(ri)为重叠积分的平方和[2]或为原子电荷密度[17].

原始模型中的φ(ri) 为抛物线型函数，当将截断距离扩展到第三近邻时，使用原函数形式给出了不合理的原子间相互作用，为此本文修正该函数为四次幂形式:

原始模型中的对势函数V(r)为四次多项式，本文修正为六次多项式:

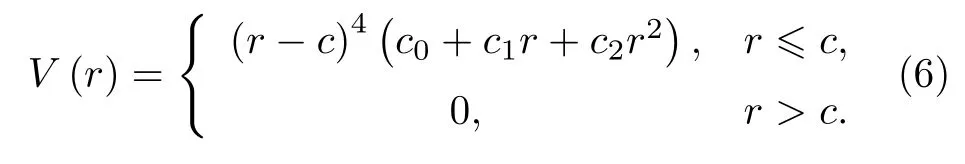
函数形式的选择和c与d的取值在后面详细讨论.c与d是截断参数，选取在第三近邻与第四近邻之间，c和d的值分为:

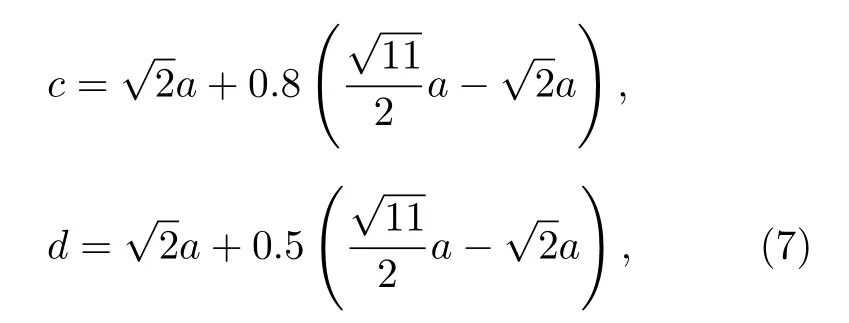
其中，a为Nb的晶格常数.

3 截断处理方法

为了减少分子动力学模拟计算原子受力所用时间，通常不采用相互作用减少到零的自然截断的方式，而是在一个方便的力程上将原子间相互作用截断.有研究表明，如果预先不做截断处理，计算一个分子动力学步的99%的时间都将用于计算使粒子运动所需的力.

如果势能不是光滑截断，那么在截断点上的力就会出现δ函数形式的奇异性，因此，必须考虑势能的截断对系统特性的影响.首先需要保证势能及其一阶、二阶导数在截断点连续.势能对距离的一阶导数对力有影响，势能对距离的二阶导数对材料的弹性常数、体模量、剪切模量等有影响.这些函数是否连续、力程的大小对材料的结构稳定性、力学稳定性、相变等都有影响.

可以采取多种方法对势函数进行截断，如:1)简单地将函数平移; 2)将函数在适当位置截断，再增加截尾函数; 3)在适当位置迭加一个截尾函数; 4) 将截断函数直接包含到势函数表达式中.

其中方法1)比较粗糙，且不能保证势函数的一、二阶导数连续，只适合做静态的与能量相关的计算.方法2)和方法3)需要增加参数的数量，以保证在函数连接点的各阶导数连续，且要慎重考虑连接点的选取.方法4)是目前使用比较多的方法，优点是与势函数同时进行参数拟合.目前常用的主要有两种形式，一是Finnis和Sinclair使用的阶跃函数的形式

即在选取的势函数上直接乘以H(x); 另一种是Mishin[23]使用的截断方式，

也是在势函数上直接乘以ψ(x).

4 原子间势与晶体性质

不论是拟合原子间势还是检验原子间势，均需建立原子间势与拟合晶体性质参数及检验晶体性质参数之间的关系.本文建立了内聚能、平衡点阵常数、体模量、表面能、空位形成能、间隙能及切变模量之间的关系.

对于体心立方晶体，设晶格常数为a，平衡态下的原子体积，Ωe=a3/2.本文构建的原子间势的相互作用在原子的第三和第四近邻之间截断.bcc晶体第一近邻有8个原子，距离为第二近邻有6个原子，距离为a; 第三近邻有12个原子，距离为

采用(10)式的符号来标记不同近邻下的对相互作用及电子密度，

4.1 压力和体模量

其中，PN和PP分别表示为N体相互作用和两体相互作用部分的力.由

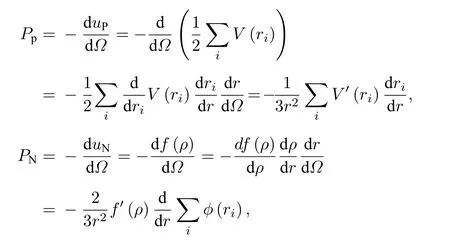
得

当r=a时，可得到平衡状态下的压力:

由

得

当r=a时，可得到平衡状态下的体模量:

4.2 表面能

表面能Esurf的计算公式为:

其中，Es为具有表面时体系的总能，Et为不包含表面时体系的总能，S为计算体系表面的面积.考虑(100)面截断距离内原子能量的变化， (100)面的表面能为:

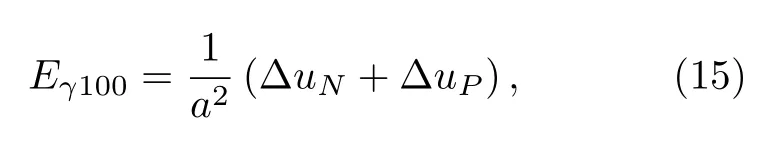
其中，

4.3 未弛豫空位形成能

单空位形成能为:

其中，En—1为具有n个原子的晶体在其内部产生一个空位时体系的总能，En为具有n个原子的理想晶体体系的总能.考虑空位周围截断距离内原子能量的变化，即为单空位形成能.

4.4 内聚能

在FS势下，每个原子的内聚能为:

4.5 平衡条件

平衡状态下，晶体内各原子受力为零，总能量最低，即utot关于r的一阶导数为0.因此，当r=a时的平衡条件为:

其中，

4.6 自间隙形成能

自间隙形成能的计算公式为:

其中，En表示具有n个粒子的理想晶体的总能量，En+1表示存在一个间隙原子时体系的总能量.本文考虑图1所示的6种间隙构型.

本文采用计算缺陷范围内的原子间相互作用能量变化的方法计算每种间隙的形成能.八面体、四面体及挤列子3种间隙构型中，在截断距离内的每个原子除了距离的原子有8个，距离为a的原子有6个，距离为的原子有12个外，还增加了一个间隙原子的相互作用，截断距离内的这些原子与间隙原子的距离及等价原子数见表1.哑铃构型中，截断距离内的原子分布要复杂一些，可通过Materials Studio软件建立相应的构型，再分析近邻原子分布情况.

图1 bcc结构6种间隙构型Fig.1.Six interstitial configurations of bcc structure.

表1 截断距离内的各间隙原子的距离及等价原子数Table 1.Distance and equivalent atomic number of each atom withinthe cutoff distance from the interstitial atom.

根据间隙原子的近邻分布可计算间隙原子的形成能.

八面体间隙形成能为:

其余构型的间隙形成能可采用同样方法计算.

4.7 立方晶体的切变模量C44和C'

我们知道，应变能密度为

其中，σij=Cijklεij.

按照Voigt记法，可得应变能密度为

立方晶体有两个切变模量C44和C′(≡(C11—C12)/2).

对于C′，考虑立方晶体的平面应变，X方向伸长时应变为ε11，Y方向缩短时应变为ε22，Z方向不变时应变为0.保持体积不变，则ε11= —ε22.对于C44，相当于在[011]方向的拉伸，只有应变为ε12，将应变分量代入(24)式，得到两种应变下的应变能密度分别为

可得

应变能密度W为单位体积的内能，则

经推导(见附录A)得

根据(31)式给出的体模量、切变模量，柯西压与弹性常数之间的关系，可在这些量之间相互计算，

5 原子间势拟合

势函数表达式(3)式和(6)式中的c0，c1，c2，A是势函数参数，本文通过拟合金属Nb的内聚能、平衡点阵常数、体模量、表面能及空位形成能的实验数据获得，实验数据[2]见表2中第1行数据.

根据第4节中建立的晶体性能与势函数的关系，然后采用均方差最小方法，调整势函数参数的大小，使得势函数能再现这些晶体性能，拟合得到的原子间势参数见表3中第1行数据，使用所得的原子间势计算的晶体性能列于表2中第2行.

从表3可以看出，拟合的均方差非常小，因此，利用所建原子间势计算的晶格常数、内聚能、未弛豫空位形成能、体模量的结果与实验值完全相同，只有表面能有微小差别.

表2 拟合用金属Nb的实验数据及计算结果Table 2.Experimental and calculation data of metal Nb for fitting interatomic potential.

表3 金属Nb的FS势参数及拟合均方差Table 3.FS potential parameters of metal Nb and fitting mean square error.

6 势函数的检验与应用

6.1 弹性常数

根据第3节建立的势函数与晶体性能的关系，利用所得势函数计算了金属Nb的3个独立的弹性常数及柯西压力.结果见表4中第2行数据.从表4中数据可以看出，除了C44偏差较大外，其余结果均较接近实验值.

6.2 间隙形成能

根据第3节建立的势函数与晶体性能的关系，利用所得势函数计算了Nb的不同间隙构型的间隙形成能，结果见表5.其中， FS(87)一列数据是文献[22]作者使用修正的FS势计算的弛豫的间隙形成能.为了便于与本文的数据进行比较，本文使用文献[22]的势函数计算了各种间隙构型的未驰豫间隙形成能，列于表4中“FS(87)未弛豫”一列.

从表5可以看出，各种方法计算的间隙形成能中，或者〈110〉哑铃构型的间隙能最低，或者是〈111〉哑铃构型的最低，本文的计算结果也是〈110〉哑铃构型最低.但是本文的计算结果普遍偏大，分析其原因，一方面我们的计算结果均未进行弛豫，另一方面，说明我们所建的势函数在近距离处排斥力过大，曲线偏硬.

表4 金属Nb的弹性常数(单位为1011 Pa)Table 4.Elastic constants of metal Nb (in 1011 Pa).

7 势函数的修正

为了使所建立的势函数能更好地描述间隙形成能，我们对势函数在近距离的行为进行修正，尝试加入修正项进行软化处理，即将对势函数表达式(6)式在第一近邻之内减去一项，

其中修正项形式如下，且仅在第一近邻内有效，

按照前述方法重新拟合势参数并进行检验.发现加入修正项后拟合得到的势参数几乎没有变化，利用修正后的势函数计算的各构型的间隙形成能均减小，但与文献数据仍有一定的偏差，为此继续对势函数进行修正.

将间隙形成能的计算值[24]作为目标值，调整修正项的幂次，当取修正项形式为(34)式时，计算结果接近目标值.

修正前后的对势曲线、有效对势曲线及电子密度曲线如图2所示，为了便于比较，同时绘出了文献[2]，及按文献[2]函数形式将截断距离扩展到第三近邻的函数曲线.

表5 金属Nb的间隙形成能Table 5.Interstitial formation energy of metal Nb.

由图2(b)和图2(c)可以看出，原始势函数曲线(文献[2])在近距离处表现出吸引行为，文献[21]通过在小于第一近邻范围叠加一项B(b0—rij)3exp(—αrij)函数来增加排斥力，修正了这种偏软现象，其中B，b0，α为势参数; 文献[22]通过对比分析由原子间势计算的力和实验数据之间的差别，在小于第一近邻范围叠加了一项K(r1e—rij)n函数，修正了原函数在近距离偏软的现象，其中K和n为势参数.

图2 势函数曲线 (a) 电子密度曲线; (b) 对势曲线; (c) 有效对势曲线Fig.2.Potential function curve: (a) Electron density curve;(b) potential curve; (c) effective pair potential curve.

我们知道，从能量对距离的导数可以获得力，从曲线形状来看，能量曲线的斜率越大，排斥力越大.从数学上考虑，对于函数(x0—x)n来说，x＜x0时，随着n的增加，曲线的斜率将越来越大，因此，通过几项幂函数的迭加形成的多项式可以获得比较满意的曲线形式.由于近距离处的原子之间相互作用对间隙能的影响较大，因此本文将间隙形成能作为目标值，通过调整多项式的幂次及系数，最终得到(34)式的修正项，使用获得的加修正项的Nb势函数计算的间隙形成能接近理论计算结果.

8 讨论

8.1 函数形式对势函数性能的影响

从势函数与晶体性能的关系表达式可以看出，势函数值及势函数的一阶、二阶导数值对材料性能的各个物理量的影响.如: 从(11) 式、(20)式可以看出对势函数、电子密度函数在第一、二、三近邻处的斜率对压力P、平衡条件有影响; 从(13)式、(27)式—(30)式可以看出对势函数、电子密度函数、以及多体相互作用项f(ρ)在第一、二、三近邻处的斜率、曲率对体模量B及弹性常数有影响; 从(15) 式—(18)式及(21)式可以看出对势函数、电子密度函数，以及多体相互作用项f(ρ)在第一、二、三近邻处的值对与能量相关的物理量，如表面能、空位能等有影响.比较拟合所得势函数计算的各物理量与实验值或理论值来修正势函数曲线.如本文中根据间隙能的结果调整对势曲线在近距离的行为，进而达到修正势函数的目的.

本文也尝试以修改势函数曲线形式来考察拟合结果的变化.原始文献[2]电子密度函数及对势函数形式为

为方便讨论，几种函数形式的截断距离均选取如下形式:使用不同形式的电子密度函数及对势函数形式利用表2中的实验数据拟合获得的势函数参数见表6.

由表6可以看出，前3组数据的拟合参数不同，是因为函数形式不同.后3组的势参数完全相同，是由于本文在拟合势参数时使用的拟合数据a，及都是平衡态下的数据，这些数据只与平衡态下曲线在第一、二、三近邻处的值、斜率及曲率有关，而后三组势函数只对小于第一近邻部分的曲线进行修正，这种修正并没有改变曲线在第一、二、三近邻处的值、斜率及曲率，因此拟合获得的势函数参数没有改变.也就是说，当使用平衡态下的数据作为拟合数据时，调整势函数曲线只要不改变曲线在各个近邻处的值、斜率及曲率，拟合的势参数就不变.

使用获得的各个势函数计算表1中的晶格常数、表面能、空位能及体模量在均方差范围内与实验数据一致.除拟合数据之外的各物理量的计算结果见表7.

从表7可以看出，第1列数据与表4的弹性常数及表5的间隙形成的计算值相差悬殊，特别是C'出现了负值的情况，表明原始的势函数形式不适合于扩展到第三近邻.第2列数据修改了原始的对势函数，将四次多项式修改为六次多项式，保持电子密度为原始函数形式，结果有所改善，但与实验值相比仍然相差很大.第3列为本文提出的函数形式，将电子密度修改为四次幂的形式，将对势修改为六次多项式的形式，弹性常数的结果有了明显的改善，但是间隙形成能的结果仍然远高于实验值.第4列和第5列数据为分别使用(33)式和(34)式对本文的对势函数进行了修正，也就是对小于第一近邻部分的对势曲线进行了软化，结果表明对弹性常数几乎没有影响，原因与前述对势参数的影响相同，本文这种对对势函数在近距离处的软化处理并没有改变对势曲线在第一、二、三近邻处的值、斜率及曲率，而平衡态下的弹性常数只受平衡态下原子间势函数在各个近邻的值、斜率及曲率的影响，因此这种修正对弹性常数的计算结果没有影响.第4列数据的间隙形成能与前3列数据相比明显降低，而第五列数据为根据间隙能的实验结果对本文的对势函数进行的进一步修正的结果，可以看出间隙形成能稍高于实验数据，这是可以理解的，因为本文计算的间隙能是未弛豫的.表明本文的这种软化修正影响间隙能的结果.这是由于间隙原子与近邻原子的距离往往小于bcc结构的第一近邻，而近距离排斥力大，表明晶体比较硬，这时向晶体中放入一个间隙原子将需要大的能量; 当排斥力减小时，表明晶体变软，这时向晶体中放入一个间隙原子所需要的能量将减小，因此间隙能降低.

表6 不同函数形式的势参数Table 6.Potential parameters of different functional forms.

表7 不同函数形式的各物理量计算结果Table 7.Calculation results of each physical quantity in different function forms.

8.2 截断距离对势函数性能的影响

为了考察截断距离对势函数性能的影响，本文使用修正后的势函数形式即(5)式， (32)式和(34)式，计算不同截断距离下各物理量的变化.先保持电子密度函数的截断距离不变，选择不同的对势截断距离，分别拟合势函数，再利用所得的势函数计算材料的各种物理量，对势函数的截断距离形式为:

当x分别取0.55， 0.7， 0.80时，各种物理量的计算结果如表8所示.

表8 不同对势截断距离下的各物理量计算结果Table 8.Calculation results of each physical quantity under different pair potential cutoff distance.

表8中前4行数据为拟合数据，在均方差范围内与实验结果一致.第5—9行为与力学性质相关的数据，几种截断距离下，结果差别不明显.后6行数据为间隙能的计算结果，可以看出，间隙形成能变化不明显，但x= 0.8时的均方差最小.

随后，本文先保持对势函数的截断距离c=不变，选择不同的电子密度函数的截断距离，分别拟合势函数，再利用所得的势函数计算材料的各种性能，电子密度函数的截断距离形式为

当y分别取0.45， 0.50， 0.60时，各种物理量的计算结果如表9所示.

表9 不同电子密度截断距离下的各物理量计算结果Table 9.Calculation results of each physical quantity under different electron density cutoff distance.

从表9可以看出，前4行数据为拟合数据，在均方差范围内与实验结果一致，其余弹性常数及间隙形成能的结果均变化不大，在本文的情况下，电子密度的截断距离对势函数的性能影响不大.本文的截断方式没有改变曲线在各个近邻处的值、斜率及曲率，并且本文没有计算晶体被压缩和拉伸等情况，由于在各个近邻原子范围内没有出现原子数的变化，因此截断方式对计算结果几乎没有影响.但是如果采取其他方式对函数进行截断，如(9)式的形式，则不同的截断距离对曲线的斜率和曲率有影响，进而对各物理量的结果将会产生影响.另外，如果计算拉伸等体积或形状有变化的情况，如果截断距离使相同近邻原子内的原子数发生变化时，对计算结果也将产生影响，为此进行这类计算时，截断距离的选取需要慎重.

9 结论

本文从文献[2]的FS势出发，将原子间的相互作用扩展到第三近邻，构造了过渡金属Nb的原子间势，并较详细地叙述了开发原子间势的方法.研究了势函数曲线形式对晶体性质的影响，同时研究了函数形式、截断距离的选择对材料性质的描述及势函数质量的影响.得到如下结论.

1) 原始的FS势函数形式不适合原子间相互作用扩展到第三近邻.经过分析及尝试发现，修正电子密度函数为四次幂的形式，对势函数形式为六次多项式的形式时，原子间势能较好地描述原子间的相互作用.

2)以间隙形成能的结果作为目标值修正了对势函数在近距离的行为，修正后的势函数给出了接近DFT计算结果的间隙形成能.

3)当使用平衡态下的物理量作为拟合数据时，调整势函数曲线形式，只要不改变函数曲线在各个近邻处的函数值、函数斜率及曲率，对拟合的势参数没有影响，对于弹性常数的结果也没有影响，改变近距离处曲线的形状影响间隙能的大小.

4)在本文的截断方式下，改变截断距离对势参数和晶体性能的计算结果均没有太大影响.

附录A 立方晶体剪切模量与原子间势的关系

晶体中任意一点(xi，yi，zi)距原点的距离为ri=

对于C44，晶体中任意一点(xi，yi，zi)的弹性位移为δxi=ε12yi， δyi=ε12xi， δzi=0，由于应变分量是小量，故:

对于C′，晶体中任意一点((xi，yi，zi)的弹性位移为δxi=ε11xi， δyi= — ε11yi， δzi= 0，由于应变分量是小量，故

对于bcc结构金属Nb，设晶格常数为a，Ωe=a3/2 ，考虑前三层原子，第一层有8个原子，坐标为距原点距离为第二层有6个原子，坐标为 (±a，0，0) ， ( 0，±a，0) ， ( 0，0，±a) ，距原点距离为a; 第三层有12个原子，坐标为(±a，±a，0) ， (±a，0，±a) ， ( 0，±a，±a) ，距原点距离为

先计算C44，根据(25)式、(26)式及(1)式—(4)式可得