Fresnel型高阶积分的统一表达式*
2021-06-18段旭朝
黄 炜,段旭朝
(1.宝鸡职业技术学院基础部,陕西宝鸡 721013;2.宝鸡文理学院物理与光电技术学院,陕西宝鸡 721016)
0 引 言
衍射是光波动性的表现,是光传播的基本规律,点源照射的衍射较平面光照射的衍射更具一般性,对光束的传输与变换、光学系统的衍射成像以及光信息处理等方面有着重要作用[1-3].1882年,基尔霍夫建立了一个严格的数学理论,证明了菲涅尔的设想基本上正确,并修正了倾斜因子.由于基尔霍夫理论只适用于标量波的衍射,故又称标量衍射理论.菲涅尔(Fresnel)衍射积分已在多领域应用,其计算是物理光学、微波技术与天线等工程和道路工程设计与建设的一道难题.本文旨在利用复分析、伽马函数与积分变换给出的 Fresnel型高阶积分S(n)、C(n)及相关的实积分进行求解和计算,以期得到统一的表达式,解决Fresnel衍射积分在不同领域因计算带来的问题.
1 物理与工程中的Fresnel衍射积分
复宗量Fresnel积分的计算,是物理光学、微波技术与天线等工程和道路工程设计与建设计算中遇到的一个难题.
1.1 物理光学领域[4-6]


1.2 微波技术与天线等工程领域
随着信息时代的到来,作为信息载体的高频电磁波,不仅在卫星通信、计算机通信、信息传输、移动通信和射频识别领域广泛应用,还在有线电视、闭路监控系统、基站、手机天线和蓝牙耳机等器材中广泛使用.随着数字信号处理(digital signal processing,DSP)技术的迅猛发展,DSP器件性能价格比的不断提高,高频电磁波在雷达、声呐及相关军事通信领域获得成功应用.自适应天线技术在蜂窝移动通信系统中的应用是相关领域学者研究的热点问题.
自适应天线是基于Fresnel区相位修正结构聚焦的多波束自适应天线.在多波束自适应天线系数的计算等方面,其难点还是高阶的Fresnel积分计算,特别是复宗量Fresnel积分的计算[7].如在深海潜标数据实时传输及我国航天测控网建设中的远望7号测量船上的关键设备上,以及在C频段高功率功放和S频段1+1高功率功放100%国产化等国之利器上的使用,其中采用了无线连接实现实时数据传输及微波天线计算,都需要计算高阶的Fresnel积分.
1.3 道路工程设计与建设领域
回旋线,也称为缓和曲线、过渡曲线和卵形回旋曲线,即Fresnel螺旋线[8].在理论上是车辆转弯时的车轮轨迹,从直线到圆弧线、圆弧线到直线、不同半径的圆弧线之间和2个圆的同向连接或反向连接等都离不开回旋线.在高速公路、高速铁路、铁路线性、公路线性以及像汽车一样的自动机械设备的线性规划设计中,均离不开回旋曲线的使用,其可以使高速道路更好地适应车辆转弯时转弯轨迹,最大限度地缩小各种曲线的曲率及绕率突变,增大行车安全、乘车舒适感及线性美观度等.
在两段圆弧之间为G2联系设计一段缓和曲线,一段理想的回旋曲线不应包括任何拐点,其弯曲度随弧长变化逐点增加或减少.通常利用计算机辅助设计CAD来进行回旋曲线设计,理想的回旋曲线设计是非常复杂而又非常重要的,其难点是Fresnel积分定义的一个超越函数值的计算问题,由于计算难度较大,对野外测设要求苛刻.今后Fresnel积分都是指这2个积分.下面给出Fresnel型高阶积分的统一表达式.
2 Fresnel型高阶积分的统一表达式



3 几个引理


图1 CR的上半圆示意

4 定理证明
Fresnel型高阶积分不能按普通的方法进行求解和计算.
4.1 定理2.1和2.2的证明



4.2 定理2.3证明


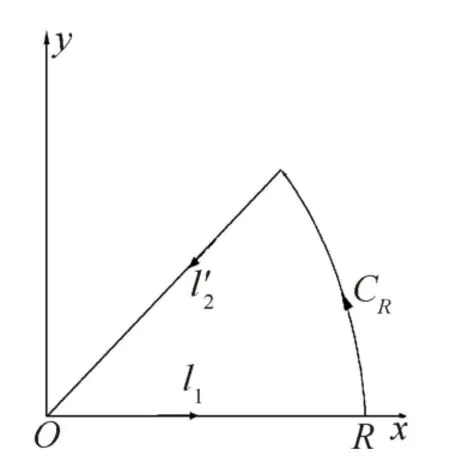
图2 CR的扇形示意

5 结束语
本文总结了Fresnel衍射积分在物理光学、微波技术与天线等工程和道路工程设计与建设计算中所表现的难题形式.并利用复分析、伽马函数与积分变换给出的 Fresnel型高阶积分S(n)、C(n)及相关的实积分进行求解和计算,得到了统一的表达式并进行了证明,彻底解决了其在不同领域因计算带来的问题.
