应变软化模型中内聚力对模拟结果影响的数值模拟研究
2021-06-18杜学领
杜学领
(贵州理工学院 矿业工程学院,贵州 贵阳 550003)
0 引 言
应变软化模型是岩体研究中常用的本构模型,尽管该模型来源于摩尔库伦模型,但在峰后特性方面,应变软化模型被认为是与真实岩体特性更加接近的模型。因此,在岩石力学及岩土、矿业工程等领域,应变软化模型应用广泛。
在FLAC3D数值模拟中,Itasca公司将摩尔库伦模型设定为理想弹塑性模型,达到峰值强度后,一般将会保持稳定;应变软化模型的峰前特性与摩尔库伦模型几乎没有差异,但在峰后则表现为脆性突然破坏或阶段性软化破坏[1]。物理实验中,往往能够观察到煤岩体的峰后软化特性,如砂岩在三轴围压下的测试表明,应变为0.005~0.04时达到峰值强度,而后进入峰后软化阶段[2];化学腐蚀作用下,黑云片岩峰值载荷所对应的应变量为0.18~0.28,化学腐蚀作用使达到峰值载荷所需的应变量增加[3];不同加载速度下,岩石的峰值载荷应变为0.28%~0.43%,而煤的应变为0.38%~0.75%,甚至可达到1%[4]。李鹏飞等[5]通过对花岗岩的三轴实验分析认为,岩石内摩擦角会随着塑性参数而变化,但残余内摩擦角与初始内摩擦角值相差不大;陆银龙等[6]通过软弱泥岩的常规三轴试验则认为,广义内摩擦角会随着围压增大而显著降低,但在峰后软化阶段基本保持不变;经纬等[7]分析认为,岩石峰后内摩擦角可近似看作是不变的;亦有研究指出含水率、粗颗粒含量、内摩擦角等对断层泥的软化特性产生主要影响[8]。可见,目前对于内摩擦角已有一定研究,但对于内聚力的评价则较少。
工程方面,基于能量原理的分析认为,煤体的应变软化特性是冲击地压的必要条件,该研究列举了煤的峰值强度对应应变约为0.005[9];李铁[10]研究认为,软煤的反复软化-硬化,使软煤在深部高应力条件也有可能发生冲击失稳,在冲击倾向性评价中,动态破坏时间、冲击能量指数、剩余能量指数等也与试件的峰后特性密切相关[11];周勇等[12]研究认为,忽略应变软化特性对于工程而言有可能存在风险;王凯等[13]也认为,采用应变软化模型要比摩尔库伦模型更适用于深部工程。
上述物理实验及相关研究表明,煤岩体的应变软化特性是客观存在的,甚至会对工程造成重要影响。但同时也说明,不同岩体达到峰值载荷的应变量不同,相同岩体在不同加载速度、不同试样处理条件下,峰值载荷所对应的应变量也不同。
数值模拟中主要通过设置内聚力、剪胀角、内摩擦角、抗拉强度、累积剪切塑性应变、累积拉伸塑性应变等参数实现应变较化[1-14]。临界抗拉强度与抗拉强度、内聚力、内摩擦角等关系密切,且峰后脆性特征与抗拉强度的设置只可二选一,而实际应用中往往主要控制内聚力、内摩擦角、抗拉强度。FLAC3D采用混合离散法显式动态有限差分解算,计算结果不仅与参数设置有关,而且还与整个模型的网格单元数量、不同时步的单元状态和不同单元间的交互作用等有关。对于岩体的非线性问题,模拟结果往往与理论模型有所差异。以往研究偏重于工程视角、参数量级、因素分析等方面,大都采用莫尔库伦模型[15-18],却未对比本构模型差异对模拟结果的影响,另对应变软化模型的软化参数设置的评价也略显不足。本文以FLAC3D中的应变软化模型为基础,着重探讨内聚力软化对模拟结果的影响。
1 研究模型建立
根据摩尔库伦破坏准则,FLAC3D中岩体破坏主要由以下条件控制[1]:
(1)
σ3=σt,
(2)
(3)
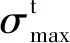
岩体有3种破坏条件:满足式(1)时,由σ1,σ3,c,φ共同决定破坏准则;满足式(2)时,最大主应力达到岩体抗拉强度时岩体发生破坏;岩体的临界拉伸强度为岩体抗拉强度或式(3)中的较小值时,岩体也会发生破坏。
由于岩体受到的主应力由加载条件和围岩网格单元的相互作用共同决定,而c,φ,σt在数值模拟中由人为指定,因此这3个参数对岩体破坏均会产生影响,应变软化参数的影响也会体现在网格单元的属性变化上。本文以内聚力作为主要研究对象,进一步探讨其他参数对模拟结果的影响。
建立直径50 mm×高100 mm的标准圆柱体试样模型,数值模型切面图如图1所示。参照CHEN J等[19]在FLAC2D中的研究方法,非加载端限制其轴向位移,加载端采用位移控制条件,边界位移速度为10-7m/step,取A,B,C3点,并利用位移差与长度比作为轴向应变,利用加载端平面内的不平衡力计算轴向应力。为方便对比模拟结果,模型基本参数与文献[19]中材料参数相同,即密度2 100 kg/m3,体积模量1.1 GPa,剪切模量1.2 GPa,内聚力3.42 MPa,抗拉强度1 MPa。文献[19]中材料的内摩擦角仅为13.8°,该数值显然与岩石物理实验存在一定差距,本文将初始内摩擦角设置为35°。在此基础上,通过改变应变软化参数,观察加载过程中不同模型的响应,并以此评价软化参数对模拟结果的影响。
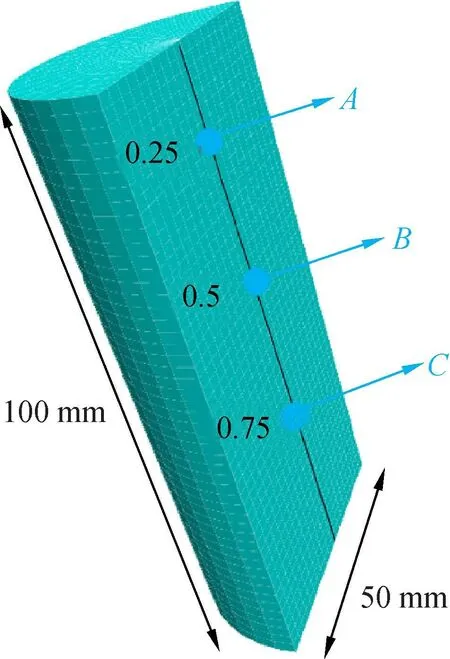
图1 数值模型切面示意图
2 摩尔库伦模型中内聚力的影响
保持其他参数不变,在摩尔库伦模型中按照25%递减改变内聚力,观察不同内聚力时模型的响应情况。图2为采用摩尔库伦模型时,不同内聚力下应力-时步演化结果。
由图2可知,采用摩尔库伦模型的应力演化具有以下特点:
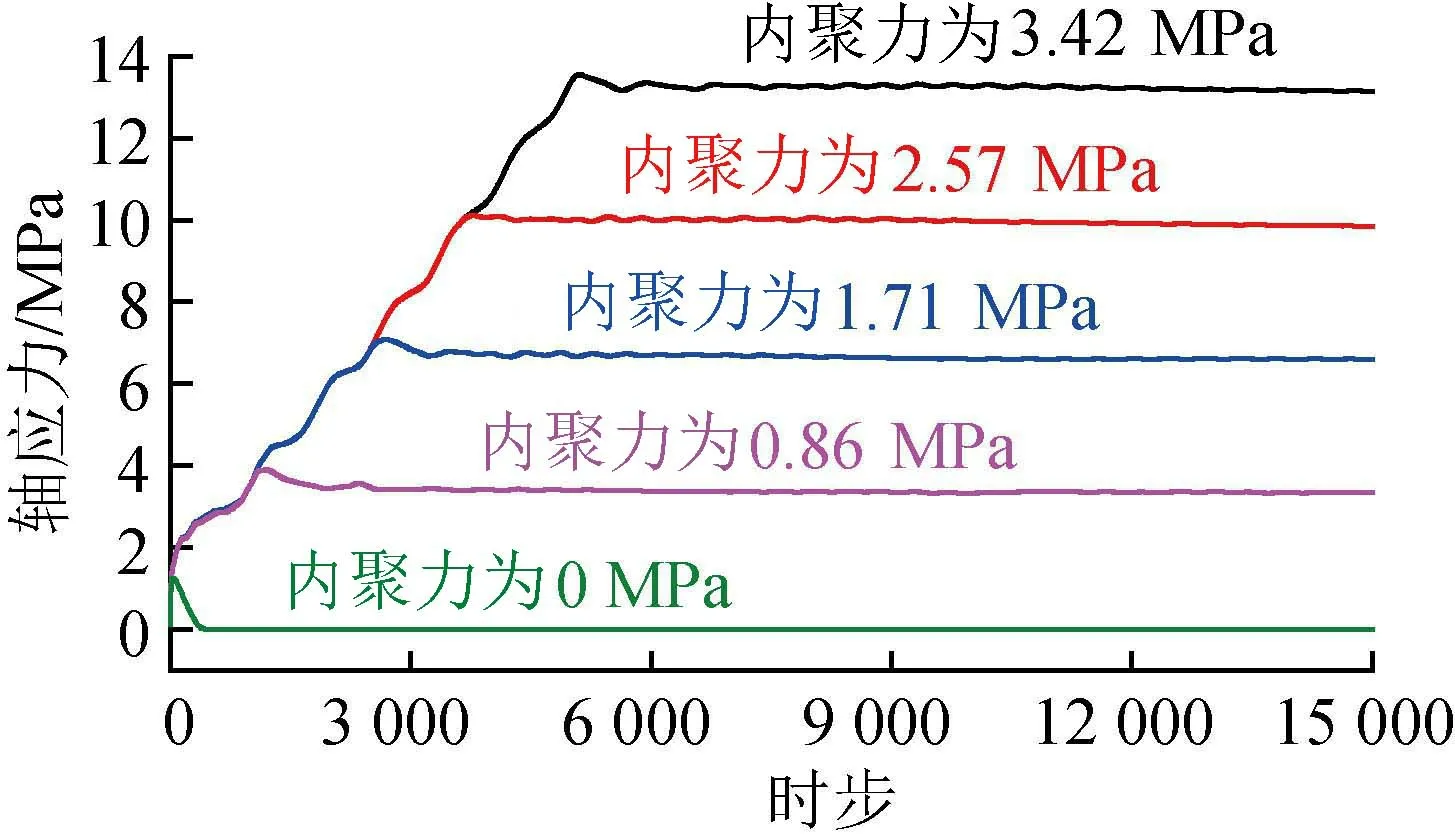
图2 摩尔库伦模型中不同内聚力下应力-时步演化结果
(1)内聚力越大,峰值强度越高。
(2)内聚力与峰值强度呈线性相关。当内聚力以25%幅值降低时,试样单轴抗压强度的峰值强度也表现出线性降低。内聚力分别为3.42,
2.57,1.71,0.86 MPa时,试样的峰值强度分别约为13.2,9.9,6.6,3.4 MPa,下降幅值分别为3.3,3.3,3.2 MPa,考虑到小数位数的保留和峰值强度波动情况,可以近似认为,试样峰值强度随着内聚力同步等幅度降低,而下降平均幅值3.3 MPa与最大的峰值强度13.2 MPa的比值也为25%,进一步说明若在模拟中保持其他参数不变而只改变内聚力,试样单轴抗压强度会随着内聚力改变进行等幅度改变,内聚力与峰值强度呈线性相关。
(3)摩尔库伦模型具有弹塑性。内聚力非0时,应力-时步均表现出弹塑性特点,但与理想弹塑性模型相比有差异:其一是达到塑性稳定状态前存在一个应力调整阶段,一般在此阶段出现最大应力,但最大应力与塑性阶段相对稳定的应力值在数值上差别不大,可以近似认为二者相等;其二是塑性阶段应力值为波动稳定状态而非绝对稳定状态,它围绕某一水平波动变化,振幅较小。
(4)内聚力为0时的特殊性。当网格单元内聚力为0时,加载初期会产生一个较小的峰值应力,约1.2 MPa,为最大峰值强度13.2 MPa的9%,但该应力出现的范围非常小,峰值点出现在前100时步以内,第500时步时应力就已经衰减到0.000 5 MPa,此后均保持在非常小的水平。对于FLAC3D的网格单元,即便内聚力为0,依然会存在力的相互作用,这与现实不完全相符;当模拟中的内聚力参数过小时,若采用应变软化模型时将内聚力软化至0,内聚力为0时的应力波动有可能会影响到模拟的准确性。
3 应变软化模型中内聚力对模拟结 果影响
3.1 软化标志点对模拟结果影响
分别设置应变软化标志点(SSP)为0.05,0.10,0.20,观察不同标志点对应不同内聚力时的应变软化效果,软化终点均为(1,0)。图3为不同应变软化参数的模拟结果。由图3可知:(1)仅改变应变软化参数时,不影响试样在峰前的表现,不同软化参数的峰前特性与摩尔库伦模型表现一致,这与FLAC3D手册中的峰后特性由塑性应变控制相一致,且在摩尔库伦模型中的峰后强度要高于应变软化后的强度;(2)其他条件相同时,峰后塑性应变的标志点越小,峰后的应变软化效果越明显;(3)其他条件相同时,峰后应变软化参数与峰前参数差值越大,峰后的应变软化效果越明显;(4)采用应变软化模型后,峰后的应力非
线性演化特征明显,相同标志点时,峰后应力跌落与内聚力的衰减并非简单的一元线性关系。相同软化程度时,不同的软化标志点与内聚力的衰减也不是简单的线性关系。标志点选取和软化程度设置使峰后软化特性更加复杂,以致不同的参数设置可能获得类似的初期峰后表现;(5)应变软化值与软化前的内聚力差值较小时,不同软化标志点时软化效果均并不明显。
3.2 软化程度与摩尔库伦模型比较
以软化标志点0.05为例,将该组模拟运算时步增加至6万,图4为摩尔库伦模型与应变软化模型的结果对比。由图4可知,对于摩尔库伦模型(MC),达到应力峰值后接近理想塑性状态,应力基本保持不变。对于应变软化的模型(SS),峰后应力表现为不断降低,软化程度越大,峰后初期应力降低较快,但经历快速降低后,应力会逐渐过渡到降低速度下降阶段,此时峰后应力缓慢降低。由图4可以看出,峰后软化特性与单纯摩尔库伦模型中内聚力参数之间的关联性并不显著,如图4所示,将内聚力软化至1.71 MPa时,与摩尔库伦模型中内聚力1.71 MPa相比,应变软化模型中的峰前依然呈现出内聚力为3.42 MPa的特征,而在峰后也不会稳定在1.71 MPa。由图4可以看出,在应变软化模型中,内聚力软化至1.71,0.86 MPa,峰后应力快速跌落,曲线快速跌落的终点值与摩尔库伦模型保持稳定的应力值接近,而当内聚力软化至2.57 MPa时,这种现象并不明显。
当内聚力软化程度足够大、软化标志点适当小时,应力快速跌落终点,与采用相同内聚力的摩尔库伦模型相当。由图3可以看出,软化标志点较大或内聚力软化程度较小时,这种现象并不明显。
产生上述现象的原因可能为:加载过程中岩体已经积累一定应力,应力增加至某一时刻达到相应的破坏条件,网格单元破坏并将属性参数重置为软化参数,该参数与采用摩尔库伦模型的相同,软化导致的参数重置和未破坏单元的应力重分布使应力快速跌落,且跌落终点与采用摩尔库伦模型相同参数时相近。随着加载不断进行,破坏单元逐渐增加,软化后的单元数量已处于主导地位,但达到软化标志终点(1,0)的单元仍占少数,因此应力跌落由快速跌落转入缓慢跌落。对于软化程度较低的参数,由于软化后的内聚力与软化前差别不明显,使峰后应力表现为缓慢下降。图3中将软化标志点设为0.2时的情况与此类似,由于峰后加载过程中较多的网格单元并没有达到软化条件,使峰后相当长的时步内软化效果并不明显。
3.3 不同监测点的应变影响
文献[19]提出利用轴向两点位移差与其距离的比值计算轴向应变,但这种方法并未评估测点是否会带来评价误差,本文选择如图1所示的A,B,C3点,并按照上述方法计算轴向应变,以软化参数(0.05,0.86)为例予以说明,图5为该示例的应变演化过程。由图5可知,达到峰值点前,不同测点获得的应变演化几乎一致,该部分所需运算时步与峰值点的时步一致,均为5 300时步左右。达到峰值点后,应变演化开始出现明显差异,包含测点A在内的计算方法在峰后应变呈现不同程度的增加趋势,应变计算的另一点距离测点A越近,峰后应变增加的越快,即AB的应变增速快于AC获得的应变增速,BC应变则呈现逐渐下降趋势,这种趋势与AB,AC趋势相反。说明即使对于同一模型,选用同样的应变软化参数,选择不同测点评价应变变化时,其结果可能不同。这与不同模型中的破坏形态有关,图6为内聚力0.86时不同模型的位移结果。
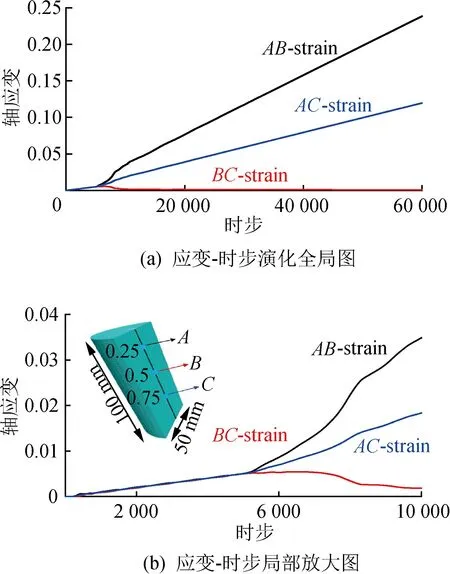
图5 应变-时步演化过程
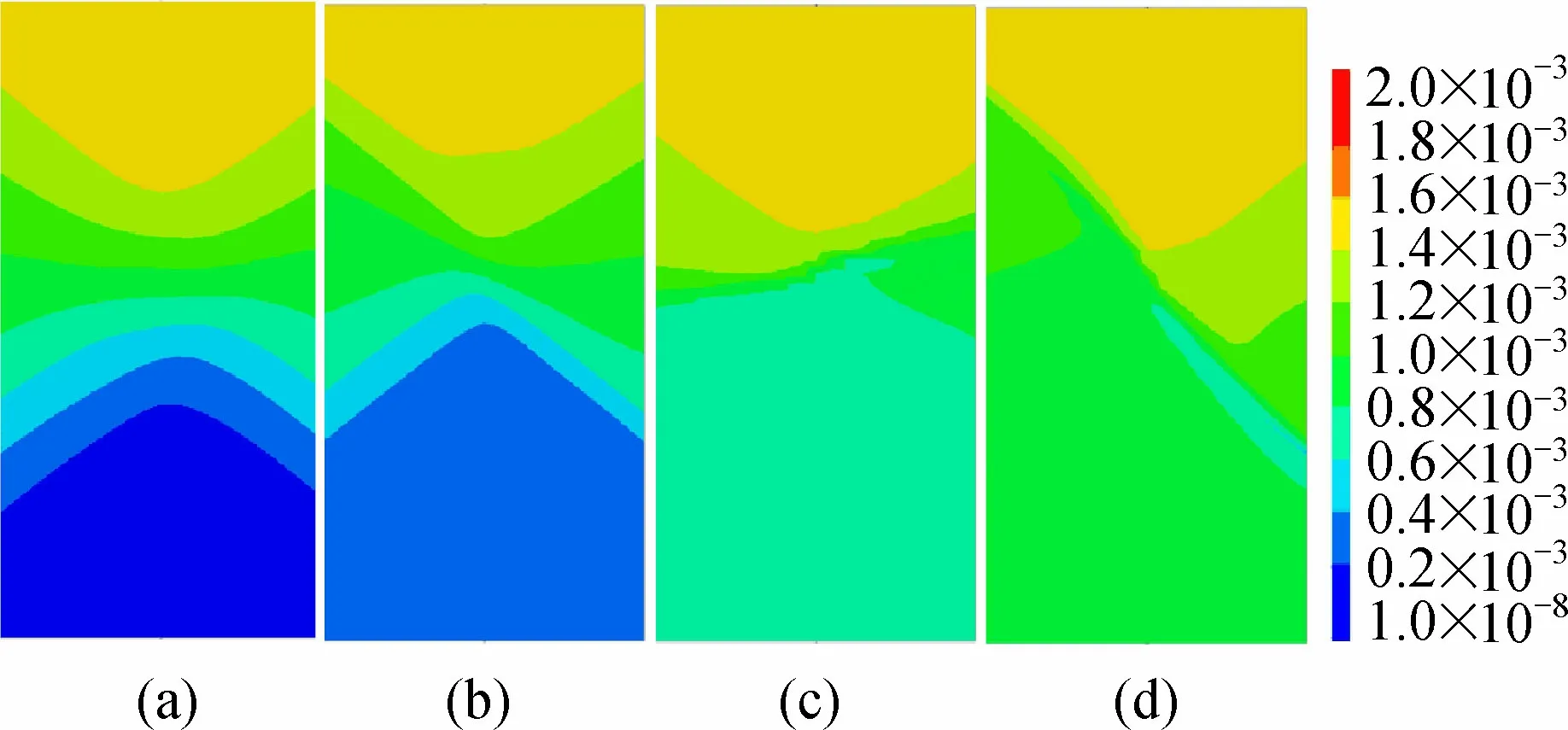
图6 内聚力为0.86 MPa时的位移结果
由图6(a)可知,对于摩尔库伦模型,在单轴压缩条件下,以圆柱体中部垂直平面为对称平面,位移近似呈对称分布。当选择不同应变软化标志点时,位移演化趋势开始发生变化,标志点选择越小,破坏越接近45°角剪切破坏,图6(d)为较为明显的剪切破坏,图6(c)表现出倾斜剪切破坏,图6(b)不明显。从位移变化量看,加载端位移大于非加载端的位移,软化越明显的模型其非对称性也越明显。对于图6(c)~(d)的剪切破坏,当测点位于不同的轴向位置时,获得的应变演化趋势也不同。文献[19]中选择的两测点位于圆柱体的上下两部分,与本文的AC选择类似,由图5可知,AC在峰后的应变增加速度低于AB,甚至在后期二者的应变差值会越来越大。可通过选取多个测点求取平均的方式缓解这一问题,但测点应与模型的破坏相一致,以避免出现BC在峰后直接应变降低的情况。
应变标志点的选择与模型整体监测获得的应变之间关联性并不明显。如图5中选择0.05为应变标志点,AB,AC,BC应变达到0.05的时步并不一致,甚至BC应变不可能达到0.05。应变标志点的选择是相对的,与模型的实际应变量无法一一对应。
3.4 抗拉强度与内聚力的协同软化效果
保持内聚力分别沿软化路径1:(0,3.42)→(0.05,0.86)→(1,0)、软化路径2:(0,3.42)→(0.05,2.54)→(1,0)不变,设置不同的抗拉强度软化路径,观察其协同软化效果。抗拉强度的软化路径分别为:方案1,同步软化路径,(0,1)→(0.05,0.25)→(1,0);方案2,快速软化路径,(0,1)→(0.01,0.25)→(1,0);方案3,慢速软化路径,(0,1)→(0.25,0.25)→(1,0)。由图7可知,同时对抗拉强度与内聚力进行软化,并未发挥出协同软化的效果,增加抗拉强度的软化参数后,应力-时步演化变化非常微小,可忽略不计。
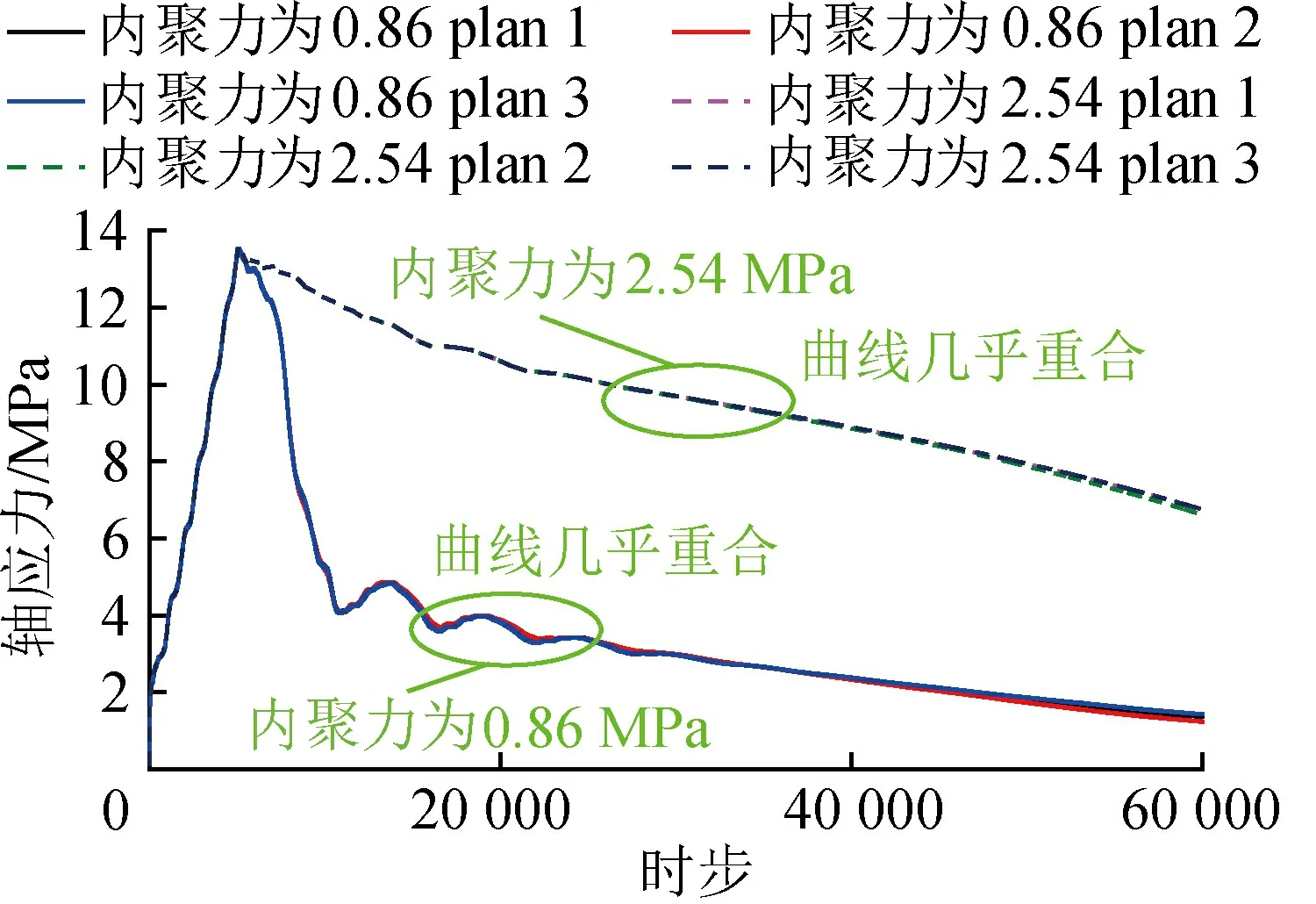
图7 抗拉强度与内聚力的协同软化模拟结果
由式(1)~(3)可知,从网格单元的破坏条件看,抗拉强度的软化效果与式(2)中的最大主应力有关,而与内聚力关系并不大。当模型中的最大主应力达不到抗拉强度时,设置抗拉强度的软化参数对模拟并无影响。即使最大主应力达到抗拉强度,但若最大主应力集中在一定区域且整体范围较小时,设置抗拉强度的软化参数对模拟的影响也是较小的。由图8可知,设软化前岩体的抗拉强度为1 MPa,达到岩体的峰值强度后,模型中较大范围的网格单元最大主应力低于1 MPa,因此,破坏准则式(2)在本文研究条件下发挥作用的范围有限。结合最大主应力和塑性区分布可以看出,该模型以剪切破坏为主,剪切破坏带的角度约为45 °,剪切破坏带的分布范围与最大主应力超过1 MPa的网格单元集中范围相一致,同时,在该剪切破坏带周围零星分布有拉伸破坏,与前文分析一致。
3.5 关于内摩擦角的讨论
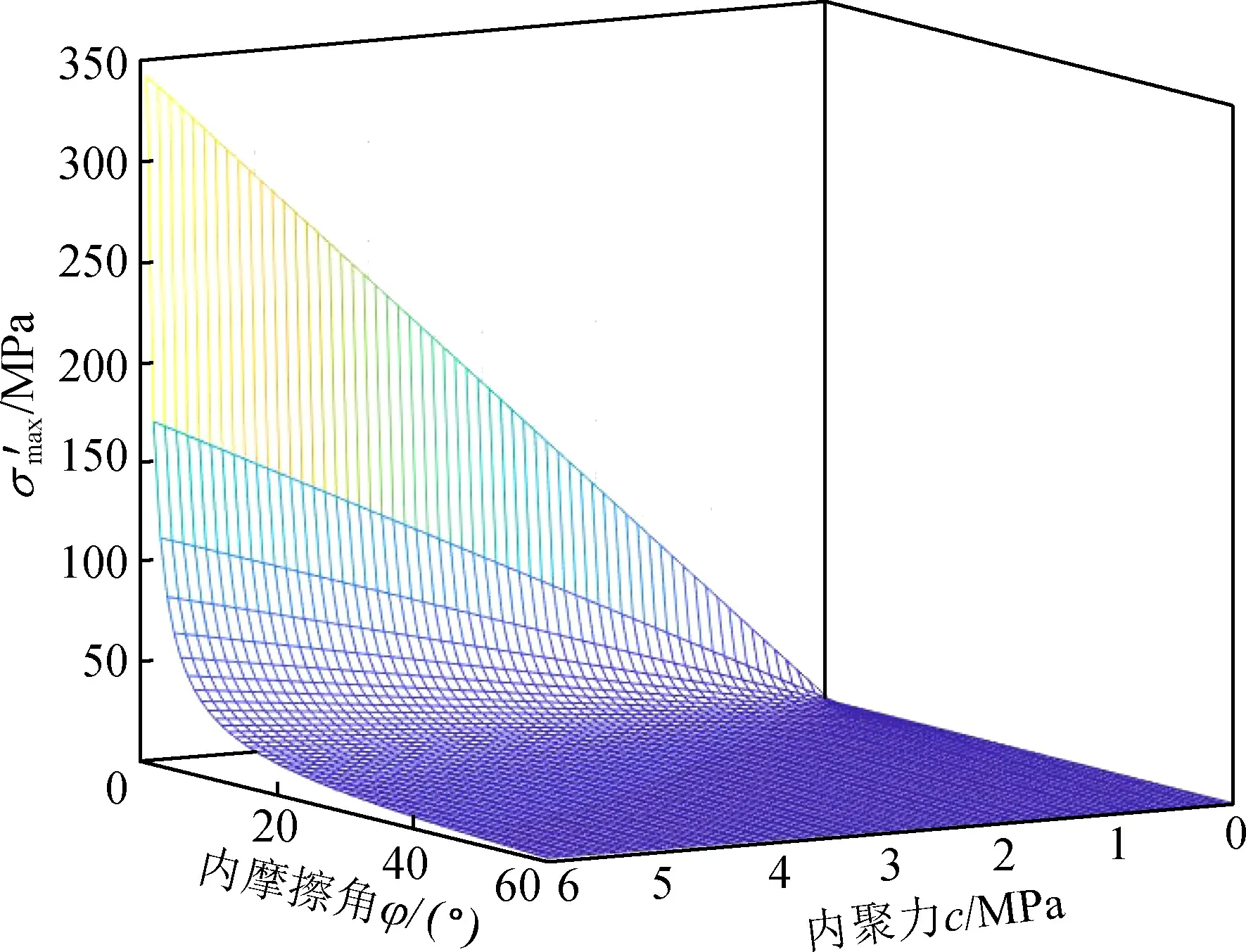
图9 式(3)的结果图
角的影响更显著,也会使式(3)结果偏大,有可能造成无法触发式(3)发挥作用。因此,对于软岩而言,在FLAC3D中将内聚力软化即可达到相应的软化效果,无需对内摩擦角和抗拉强度进行软化。
3.6 冲击倾向性评价讨论
在评价冲击倾向性时,动态破坏时间、冲击能量指数、剩余能量指数均要利用岩体加载的峰后部分。常规的数值模拟中,摩尔库伦模型峰后相对稳定,而应变软化模型则对软化参数具有较大的依赖性。因此对于确定的岩体参数,由于既定输入参数并不能反映天然岩体的离散特性,在数值模拟中通过峰后能量反映冲击倾向性很可能不够准确。按照预期选定软化参数时,已经排除了天然离散性或人为限定峰后表现,二者都无法与天然岩体的离散特性相匹配。因此,采用常规数值模拟的本构模型并利用峰后曲线计算耗散变形能、峰后破坏能密度,若以此评价冲击倾向性,则其研究结论的可靠性值得怀疑。
4 结 论
(1)采用摩尔库伦模型时,内聚力大小与峰值强度呈线性相关。内聚力为0时,模型中依然存在短时的力作用。
(2)仅改变应变软化参数时,不影响试样的峰前表现,不同软化参数时的峰前特性与摩尔库伦模型表现一致,其他条件相同时,峰后塑性应变的标志点越小,峰后的应变软化效果越明显,峰后应变软化参数与峰前参数差值越大,峰后的应变软化效果越明显,设置的应变软化值与软化前的内聚力差值较小时,在不同软化标志点时软化效果均并不明显。
(3)当内聚力软化程度足够大、软化标志点适当小时,其应力快速跌落的终点与采用相同内聚力的摩尔库伦模型相当。但软化标志点较大或内聚力软化程度较小时,这种现象均不明显。
(4)达到峰值点之前,不同测点获得的应变演化几乎完全一致,该部分所需运算时步与峰值点的时步具有一致性。但达到峰值点后,应变演化开始出现明显差异,对于同一模型、选用同样的应变软化参数,选择不同测点评价应变变化时,其结果也不同。
(5)一般在FLAC3D中将软岩内聚力软化,即可达到相应的软化效果。在常规数值模拟中通过峰后能量反映冲击倾向性很可能不够准确。
