基于高斯滤波的三维水声无线传感网络节点定位算法

王磊,刘利利,齐俊艳,宋成

(河南理工大学 计算机科学与技术学院，河南 焦作 454000)

0 引 言

地球上水资源丰富，因而，水下通信技术对水下资源探测和研究有着非常重要的意义[1]。由于受水下电磁波传输路径短、信号衰减快、介质传输速率慢等因素限制，射频信号并不适用于水下通信[2]。跟射频信号相比，声信号在水下衰减速率慢，因此水声通信(under water acoustic communication，UWAC)技术被用于水下无线传感网络(under water sensor network,UWSN)[3]。许多水下作业，比如水下污染物质量浓度探测、海底地震检测、水下目标追踪都依赖于位置信息。因此，基于水声通信的水下定位技术研究尤为重要。

水下定位方法按照定位方式可分为基于非测距的定位方法和基于测距的定位方法[5-6]。非测距定位方法主要有质心算法[7-8]和DV-hop算法[9]。该类方法对硬件要求低，受环境影响小，成本低，但是一般不能准确定位节点坐标，尤其对水下远距离节点通信容易产生较大误差[10]。基于测距的定位方法主要有RSSI算法、TOA算法和TDOA算法等。传统定位方法用于水下，性能不稳定，定位误差较大。为了满足水下定位需求，有学者提出对RSSI值采样并进行滤波处理，以提高RSSI值准确度。滤波处理方法有粒子滤波(particle filter,PF)[11-12]、秩滤波(rank filter,RF，)[13]、卡尔曼滤波(kalman filter,KF，)[14]和高斯滤波(gauss filter,GF)等。J.Sveĉko等[11]首先通过采集RSSI值获得“粒子”，根据每个粒子的重要性确定粒子权值，其次再对粒子进行重采样，最后利用粒子滤波进行位置估计；余修武等[13]提出采用RF方法对RSSI值滤波处理，以提高测距精度，再使用FTO算法对目标节点坐标进行寻优计算，得到近似最优解；ZHOU C等[14]使用KF算法处理RSSI样本，在一定程度上解决了“RSSI信号漂移”的问题，然后利用处理后的RSSI值进行距离估计和位置计算。上述算法中，PF算法存在着粒子退化或重采样粒子贫化问题，随着时间推移，KF和RF算法的累计误差会逐渐增大，且相比于高斯滤波，上述滤波算法复杂度更高。为了进一步提高定位精度，近年来，智能优化算法被引入。常用的优化算法有拟牛顿算法、粒子群(PSO)算法、差分进化(DE)算法、灰狼优化(GWO)算法以及遗传(GA)算法等。常鲁杰等[15]设计一种基于迭代粒子群优化的RQ-PSO定位算法,该算法利用MDS-MAP对传感器节点完成粗定位,引入几何约束限制粒子群初始种群范围,并采用鲁棒四边形规则对未知节点位置进行优化求解；LI J等[16]提出基于模拟退火算法的粒子群优化(SAPSO)算法，解决了在低信噪比环境下定位精度低的问题；段亚青等[17]提出的GWO算法同样也用于定位优化。但以上优化算法收敛速度慢，容易陷入局部最优。拟牛顿算法收敛速度具有快且容易跳出局部最优的优点,因此，本文提出一种基于高斯滤波和拟牛顿优化的UWSN定位方法，主要工作如下：

(1)提出基于高斯滤波的ASTL采样测距算法，通过采样，得到多组ASTL样本值，采用高斯滤波算法对ASTL样本进行加权平均，以降低因测距不准带来的误差。

(2)对估计位置进行拟牛顿优化，以得到更加准确的定位结果。

(3)通过仿真验证本文提出的算法。

1 测距模型设计

1.1 水声传输损耗模型

在水下，无线传感网络传输时由于物理层采用声信号，与电磁波信号的传输速度差距很大，因此，陆上的测距模型并不适用于水下。所以采用Urick模型，设发送节点向接收节点发送的数据包中包含发送信号强度值ST(dB)和接受节点收到数据包时记录的接收号强度RT(dB)。两节点间的传输路径损失TLloss(dB)计算式为

TLloss=ST-RT，

(1)

其中，水声传输路径损耗模型为

TLloss(d,f)≈χlgd+a(f)·d×10-3+A，

(2)

式中：TLloss(d,f)为路径传输损耗；d为传输距离，m；χ为几何扩散，χ=10时水声传播方式为柱形传输，χ=20时水声传播方式为球形传输，本文采用球形传输模型[18]；f为信号频率，Hz；a(f)为频率相关吸收系数，由公式(3)求得[17]；A为声信号在传输过程中的异常损耗,dB。

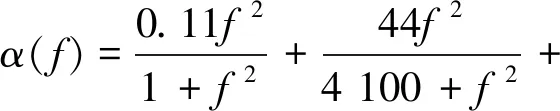
(3)

因此，由式(3)可得测距模型

(4)

由于声信号在传输过程中具有不稳定性，在某时间段内，受过往舰船或动物等产生的噪声影响，导致测量的TLloss值偏离正常值。若在测距环节按照正常数据引入测距模型中，将导致测距误差过大，定位结果不准确。传统的测距方法容易忽视声信号在传输过程中引入的偶然误差，因此，提出一种基于高斯滤波的TLloss采样距离估计方法。TLloss样本具有不等权性，使用高斯滤波能有效处理异常TLloss样本，降低因测距引入的误差，提高定位精度。

1.2 改进测距模型

(5)

(6)

(7)

式中：x为样本值;μ为均值;δ为标准差。

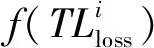
(8)

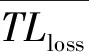
(9)

2 节点定位

2.1 位置估计

节点初始位置估计采用多边定位法，使用该方法可求得未知节点坐标的最小二乘解。根据已知锚节点坐标Pi(xi,yi,zi)与未知节点坐标P(x,y,z)，可列出方程组(10)。

(10)

其中，二维定位利用三边定位至少需要3个不共线的锚节点，而三维定位至少需要4个不共面的锚节点，所以n≥4[19]。前n-1个式子分别减去最后一个式子，得

(11)

其中，为将方程组(10)转化成矩阵乘法，作如下处理：

(12)

(13)

求解非齐次方程AX=B，解得

X=(A′A)-1*A′B

，

(14)

X即为求解的初始坐标。

2.2 位置坐标优化

2.2.1 BFGS拟牛顿法

用BFGS拟牛顿法对三维坐标求解，故可视为多变量求解问题，设向量X(x,y,z)为未知变量，拟牛顿法迭代如式(15)所示，其中Xk为第k次迭代的X值，H-1为求解问题f关于变量的二阶Hessian矩阵，gk为求解问题f关于求解变量的梯度向量。

(15)

BFGS算法是对牛顿法的改进，其思想是通过迭代方式，矩阵B近似为Hessian矩阵的逆矩阵H-1，即

H-1≈B。

(16)

正定矩阵B迭代公式为

Bk+1=Bk+ΔBk,k=0,1,2,3,…,n。

(17)

(18)

B0=I,

(19)

其中，

sk=Xk+1-Xk,

(20)

yk=f′(Xk+1)-f′(Xk)。

(21)

2.2.2 目标函数设计

对于未知节点坐标，需要满足定位误差最小，因此目标函数设计为

F(x,y,z)=minE(x,y,z)

(22)

，

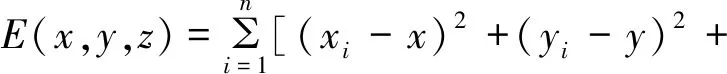
(23)

式中，E(x,y,z)为定位误差。

将式(23)展开，整理得

n(x2+y2+z2)，

(24)

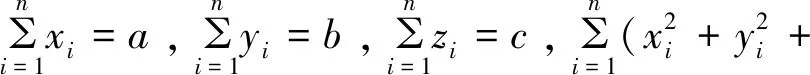
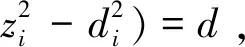
E(x,y,z)=d-2ax-2by-2cz+
n(x2+y2+z2)。

(25)

多变量的非线性方程组转化成非约束优化问题，即E函数的最小值问题。该函数作为拟牛顿优化的目标函数，通过迭代求解，得到未知节点的近似最优解。

3 算法设计

3.1 算法主要执行过程

本文定位方法把节点定位过程分为两个阶段，即离线阶段和在线阶段。定位流程图如图1所示。

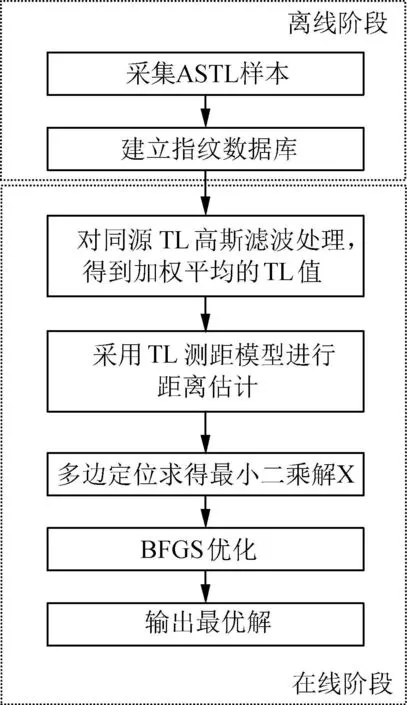
图1 定位流程图

未知节点定位步骤如下：

(1)离线阶段节点通过与邻居锚节点通信，记录邻居节点发送信号给该节点后的TL值，并存入指纹库。

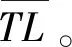
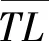
(4)采用多边定位方法，得到最小二乘解X。

(5)将步骤(4)得到的X作为初始值，采用BFGS算法迭代求解近似解。

(6)输出近似解(x,y,z)。

3.2 BFGS算法优化

对BFGS优化子流程细化，流程图如图2所示。流程步骤如下。

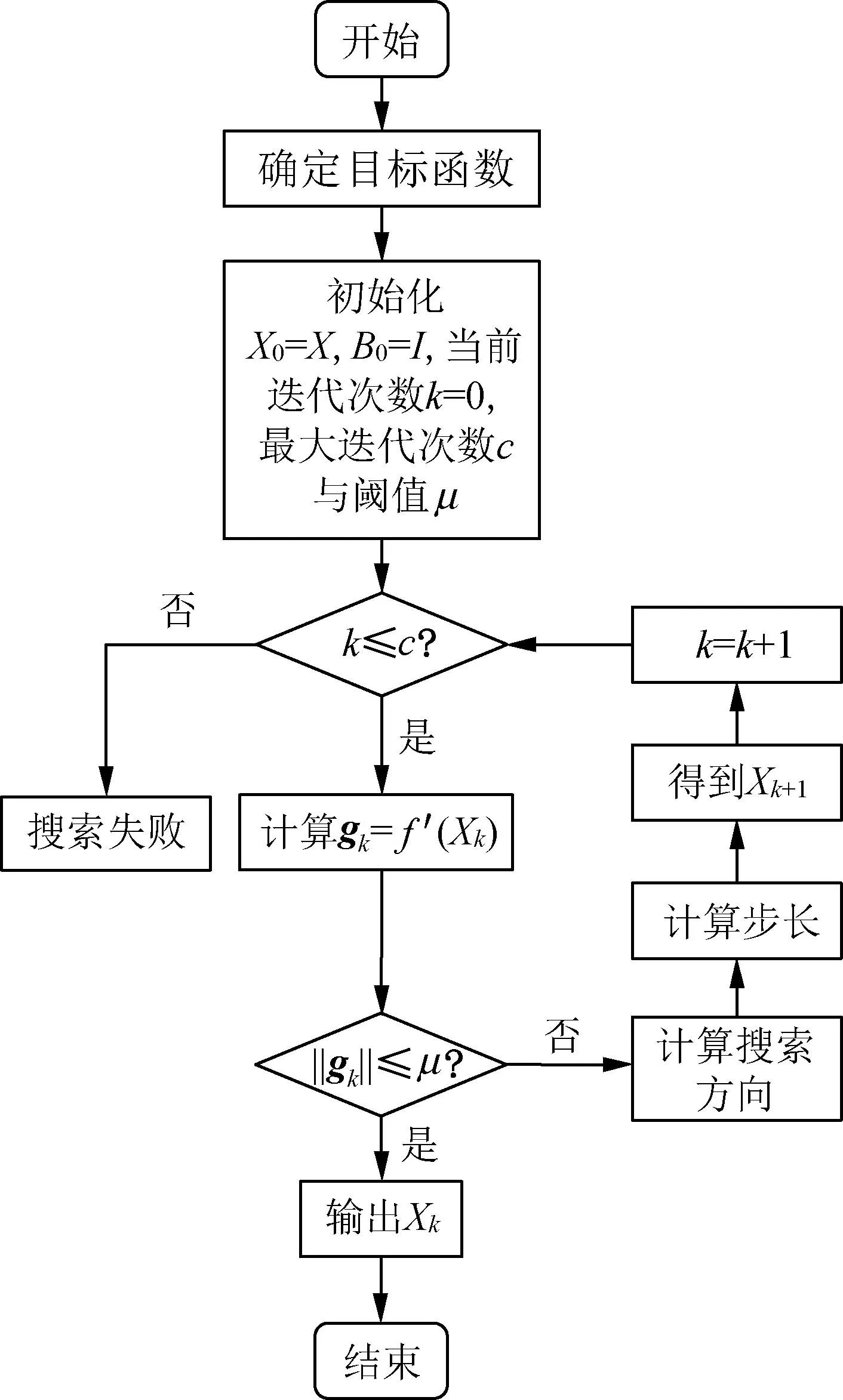
图2 BFGS算法流程图

(1)初始化参数：设置初值X0=X、误差阈值e和最大迭代次数c，并令B0=I，k:=0。

(2)若k≥c，跳出循环。

(3)否则计算f′(Xk)，若|f′(Xk)|≤ε，输出最优解。

(4)否则，计算搜索方向：dk=-Bkgk。

(5)得到步长γk，令sk=γkdk，xk+1:=xk+sk。

(6)计算gk+1=∇f(xk+1)，若‖gk+1‖≤ε，输出xk+1。

(7)否则，计算yk=gk+1-gk。

(8)根据公式(17)，进行迭代计算。

(9)令k=k+1，转至步骤(2)。

4 仿真实验

采用MATLAB2018仿真工具，仿真内容由测距优化分析和定位优化分析两部分组成。为了模拟环境噪声，在仿真环境中添加了高斯白噪声。

4.1 测距优化分析

为了对测距优化，使用仿真工具生成10 m×10 m×10 m三维水下环境。在区域内部随机部署10个锚节点和1个未知节点。节点通信半径设为5 m。未知节点可直接与所有锚节点通信。对PF、RF、KF、传统测距算法和本文提出的GF测距算法进行5组实验后，求取每组测距误差平均值，测距误差结果对比如表1所示。

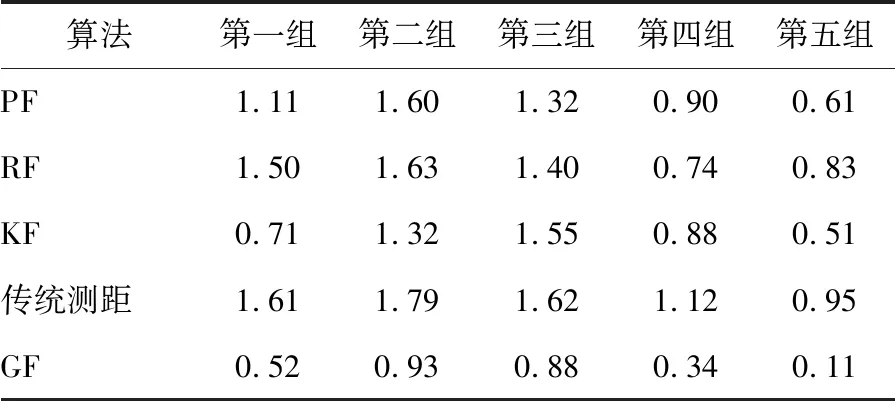
表1 测距误差结果对比表

由表1可以看出，本文提出的GF算法平均误差与PF、RF、KF、传统测距算法相比，测距优化效果最佳，最小误差可达0.11 m。

4.2 定位优化分析

针对定位优化，使用仿真工具生成100 m×100 m×100 m水下三维网络节点分布结构，如图3所示。其中，黑点为未知节点，黑色“*”为锚节点。在该区域内随机部署100个节点，其中锚节点占40%，以保证锚节点能覆盖整个网络范围。具体参数及参数值如表2所示。

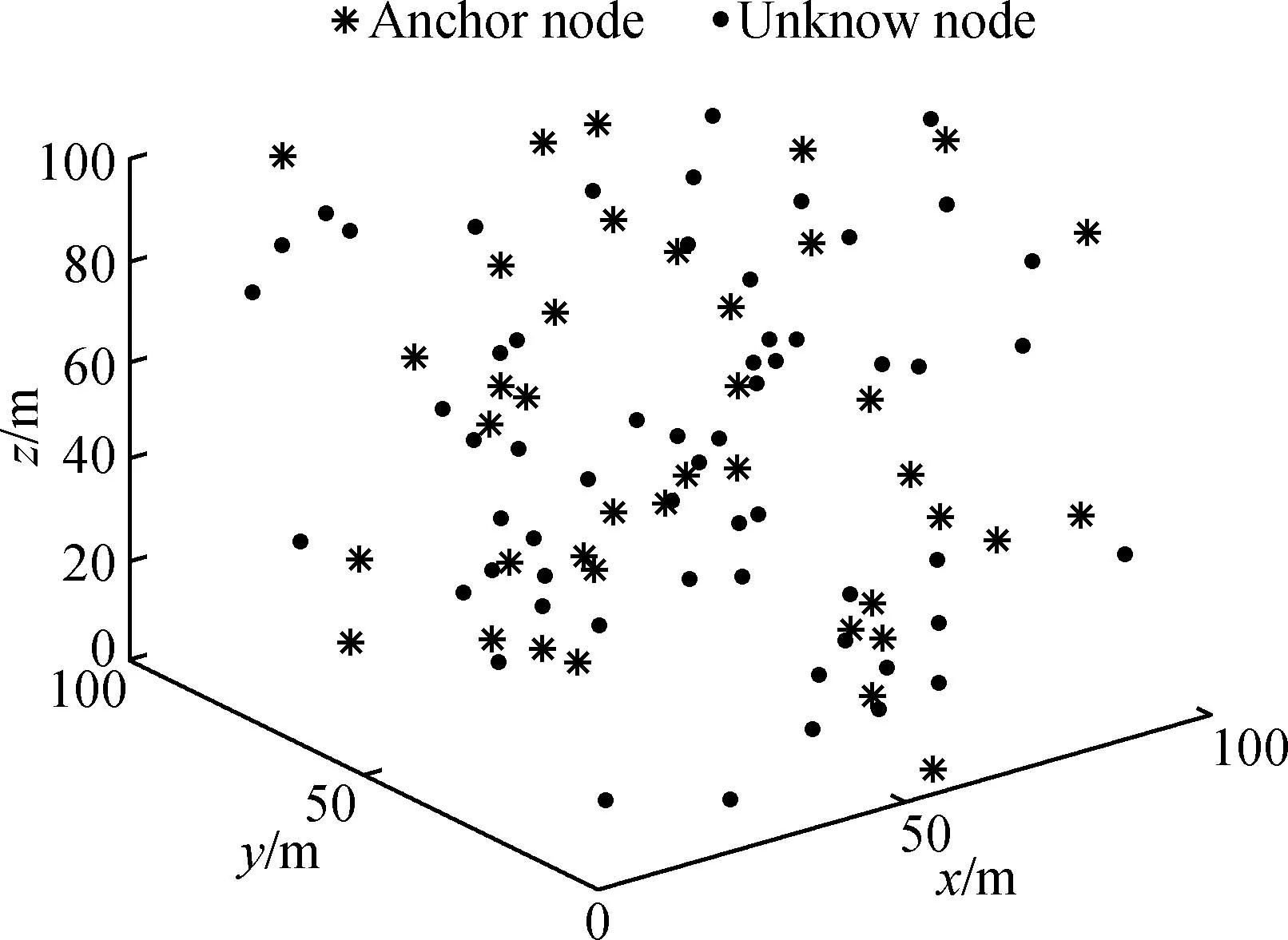
图3 节点分布图

对于每个节点，其误差定义为式(26)。其中(xie,yie,zie)为第i个被定位的估计坐标，(xit,yit,zit)为第i个被定位节点的实际坐标。

(26)

(27)

通过实验对比ASTL-RQ-PSO、ASTL-SAPSO、 ASTL-GWO和ASTL-BFGS算法，证明本文提出的算法定位误差优于其他算法。4种算法的定位误差结果如图4所示，其中横坐标为节点序号，纵坐标为定位误差。

由图4可以看出，ASTL-BFGS算法的定位误差最小，与ASTL-GWO、ASTL-SAPSO和ASTL-RQ-PSO定位算法相比，定位精度分别提高了约49%、31%和9%。图5～8为4种算法各自的定位结果，其中黑点为未知节点的估计位置，黑色短线为节点真实位置和估计位置间的偏差，黑色圆圈为不能定位的节点。图5为本文提出ASTL-BFGS算法的定位结果，节点的定位误差很小。

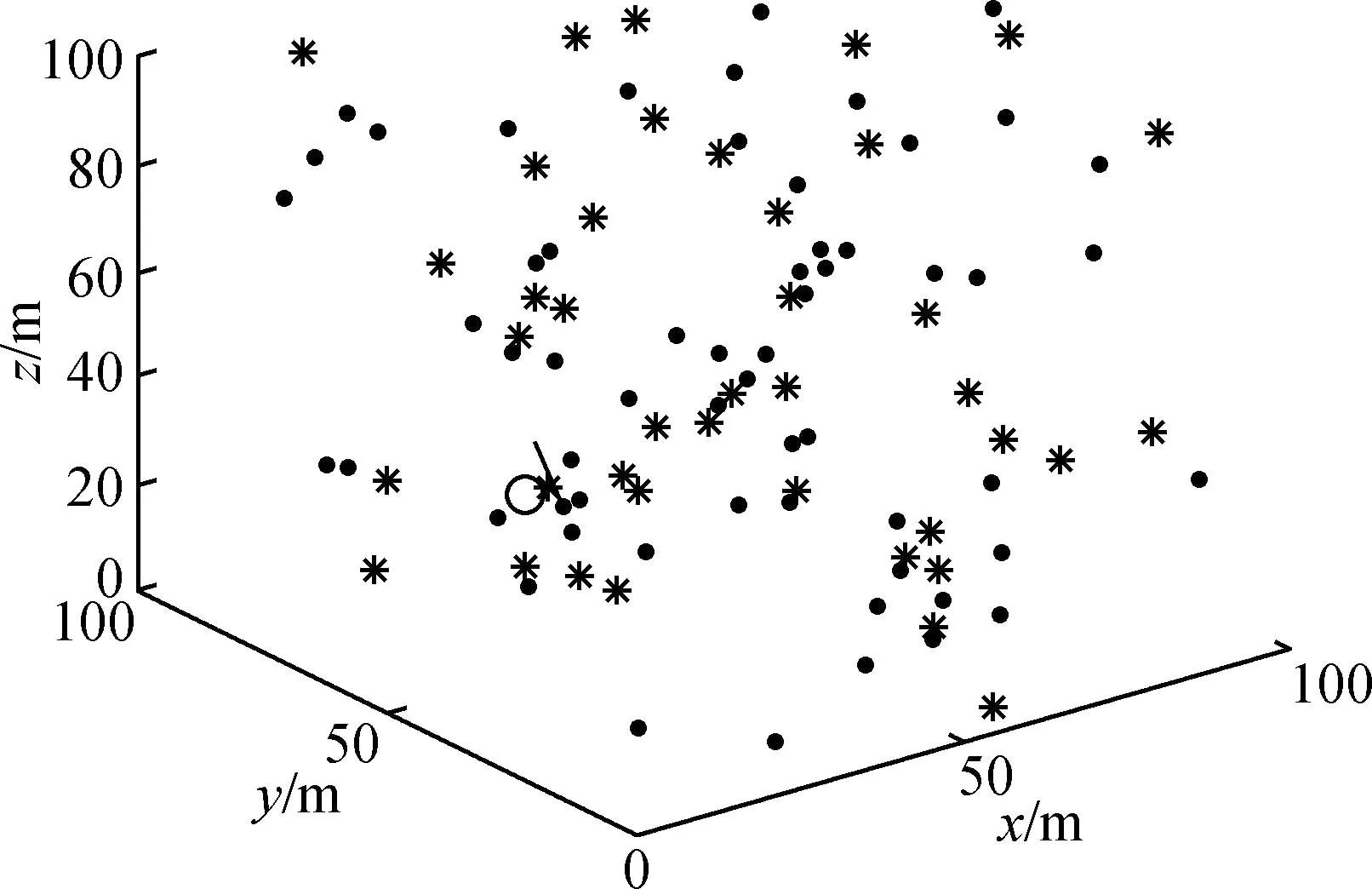
图5 ASTL-BFGS定位结果

图6～8为除本文外其他3种算法定位结果，多数节点的定位误差较大。

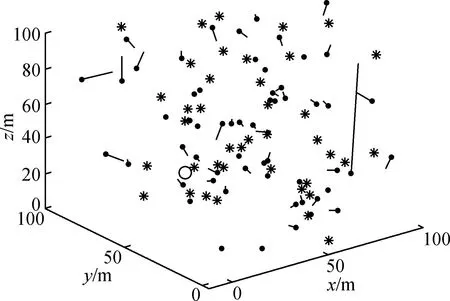
图6 ASTL-RQ-PSO定位结果

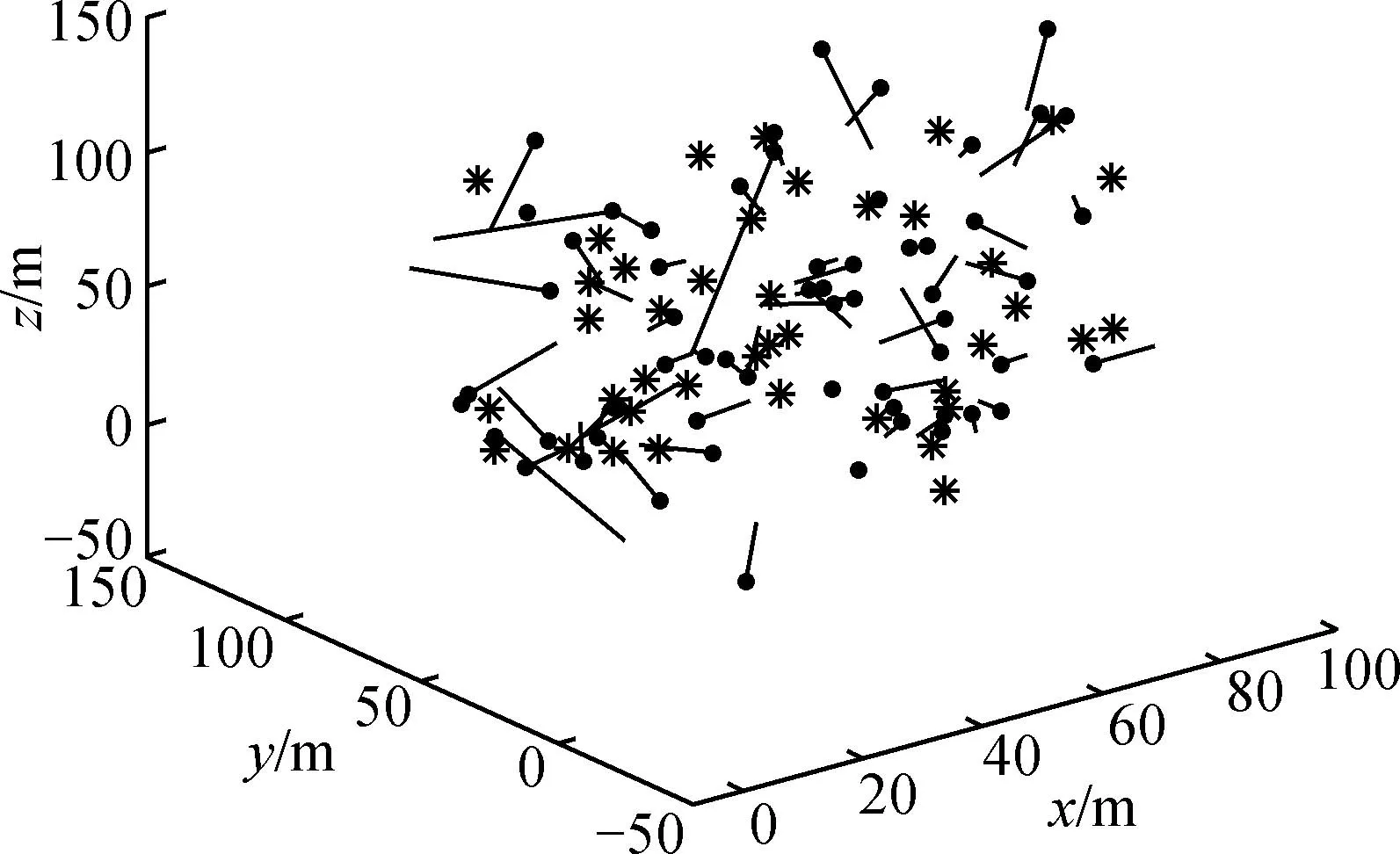
图7 ASTL-SAPSO定位结果

图9为本文提出的基于BFGS优化算法与RQ-PSO、SAPSO以及GWO 3种优化算法性能对比。由图9可以看出，随着迭代次数增加，定位误差逐渐降低，同其他算法相比，BFGS算法仅需迭代4次，定位误差便收敛至接近0。ASTL-RQ-PSO需要14次达到收敛，ASTL-SAPSO需要16次达到收敛，ASTL-GWO需要25次达到收敛，并且，ASTL-RQ-PSO、ASTL-SAPSO和ASTL-GWO 3种算法收敛后的定位误差均大于ASTL-BFGS算法收敛后的定位误差。

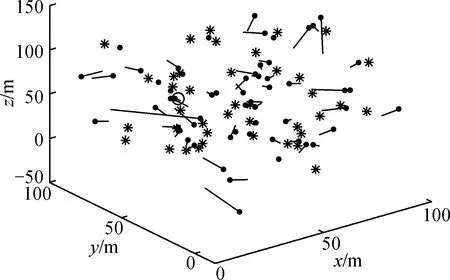
图8 ASTL-GWO定位结果

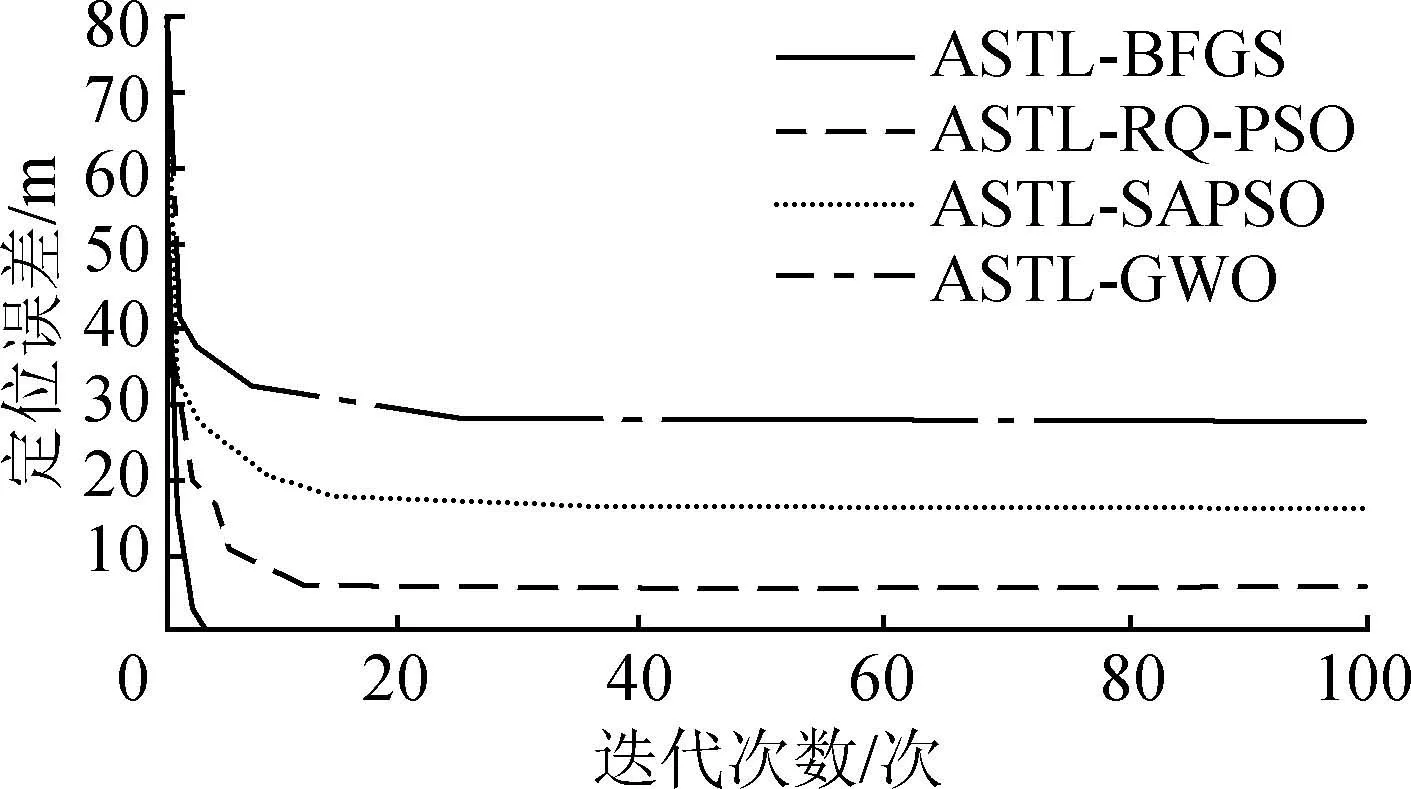
图9 BFGS、RQ-PSO、SAPSO以及GWO算法性能对比

进行两组独立实验，每组实验进行30次，并对每次实验定位结果的平均总误差取均值，以证明算法的普适性。通过分别改变锚节点数量和通信半径，以探究二者分别对未知节点定位平均总误差(以下简称平均总误差)的影响。

4.2.1 锚节点数量与定位误差实验

锚节点数量与平均总误差间的关系如图10所示。本实验中，设置节点通信半径为50 m，其余参数如表1所示。

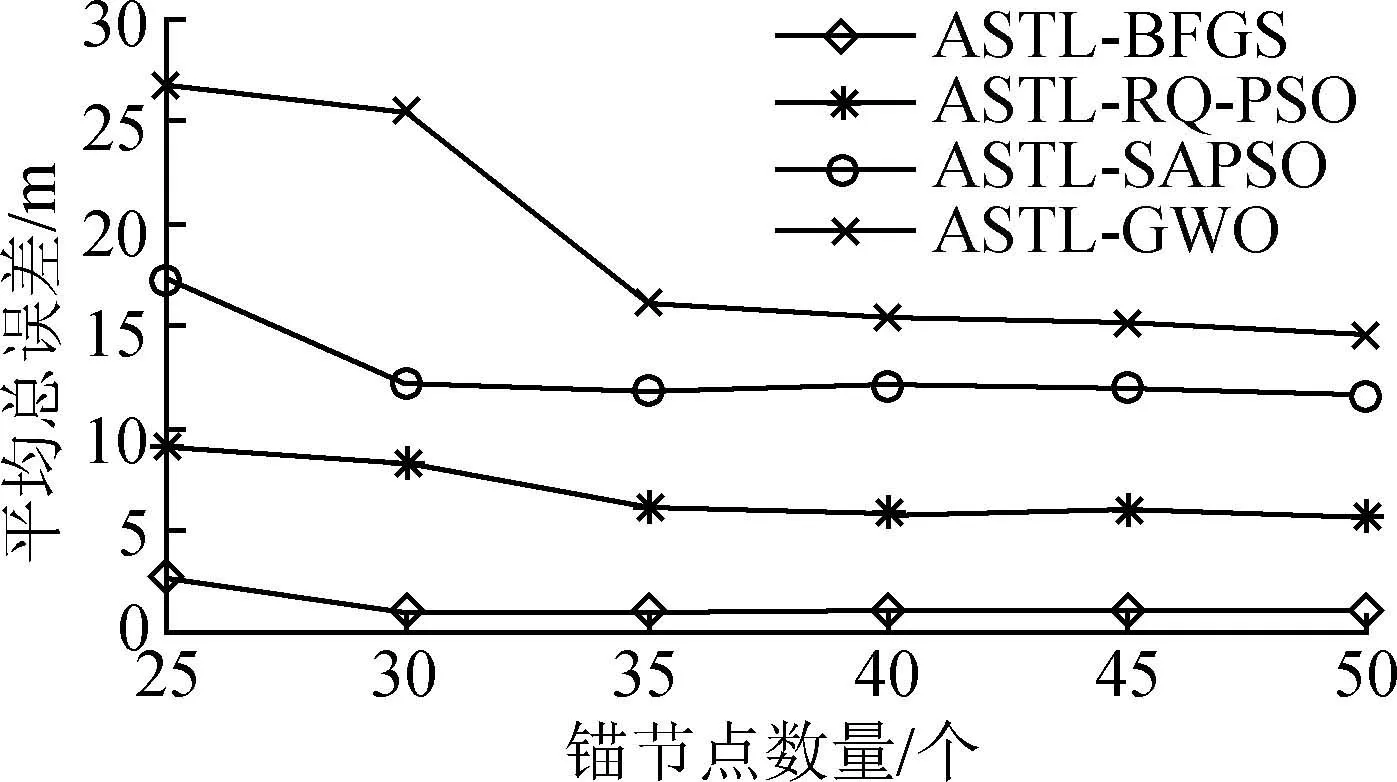
图10 平均总误差与锚节点数量关系

由图10可以看出，随着锚节点数量增加，4种算法的平均总误差逐渐减小，锚节点数量为30个时，ASTL-BPFS和ASTL-SAPSO算法的平均总误差趋向于稳定，而ASTL-RQ-PSO算法和ASTL-GWO算法在锚节点数量为35时，平均总误差才趋于稳定，且在不同锚节点数量的情况下，ASTL-BPFS的平均总误差均小于其余算法，具体数据如表3所示，对每种算法各组的平均总误差求平均值，ASTL-BFGS、ASTL-RQ-PSO、ASTL-SAPSO和ASTL-GWO 4种算法对应结果分别为1.42，6.95，12.93，18.97 m。可以看出，相比ASTL-RQ-PSO、ASTL-SAPSO和ASTL-GWO 3种算法，ASTL-BFGS的整体定位精度分别提高5.53，11.51，17.55 m。

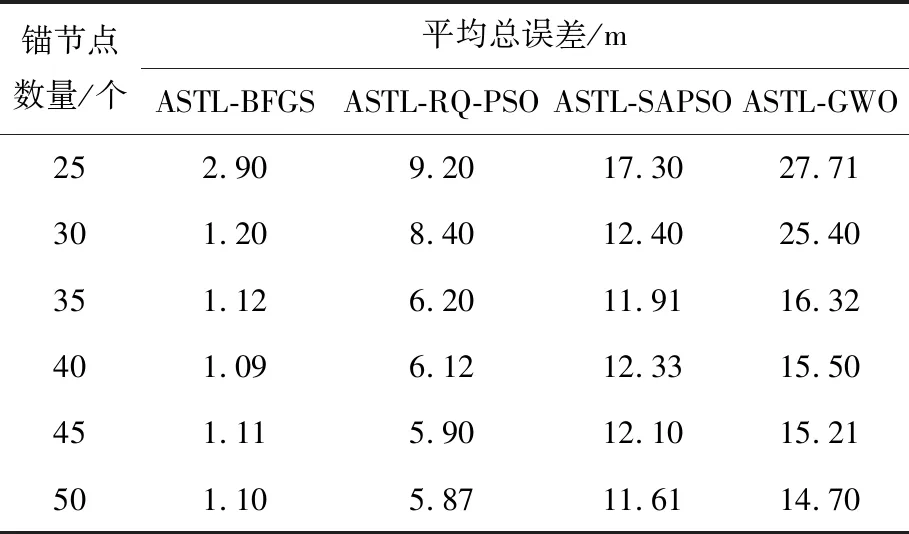
表3 不同数量锚节点时的平均总误差

4.2.2 通信半径与定位误差实验

平均总误差和通信半径的关系如图11所示。本实验中，设置锚节点数量为40，其余参数如表1所示。

由图11可以看出，ASTL-BFGS的平均总误差优于其他方法，并且随着通信半径增大，未知节点感知到的锚节点数量增多，定位误差相应减小，直到通信半径从50开始，平均总误差逐渐趋于平稳。

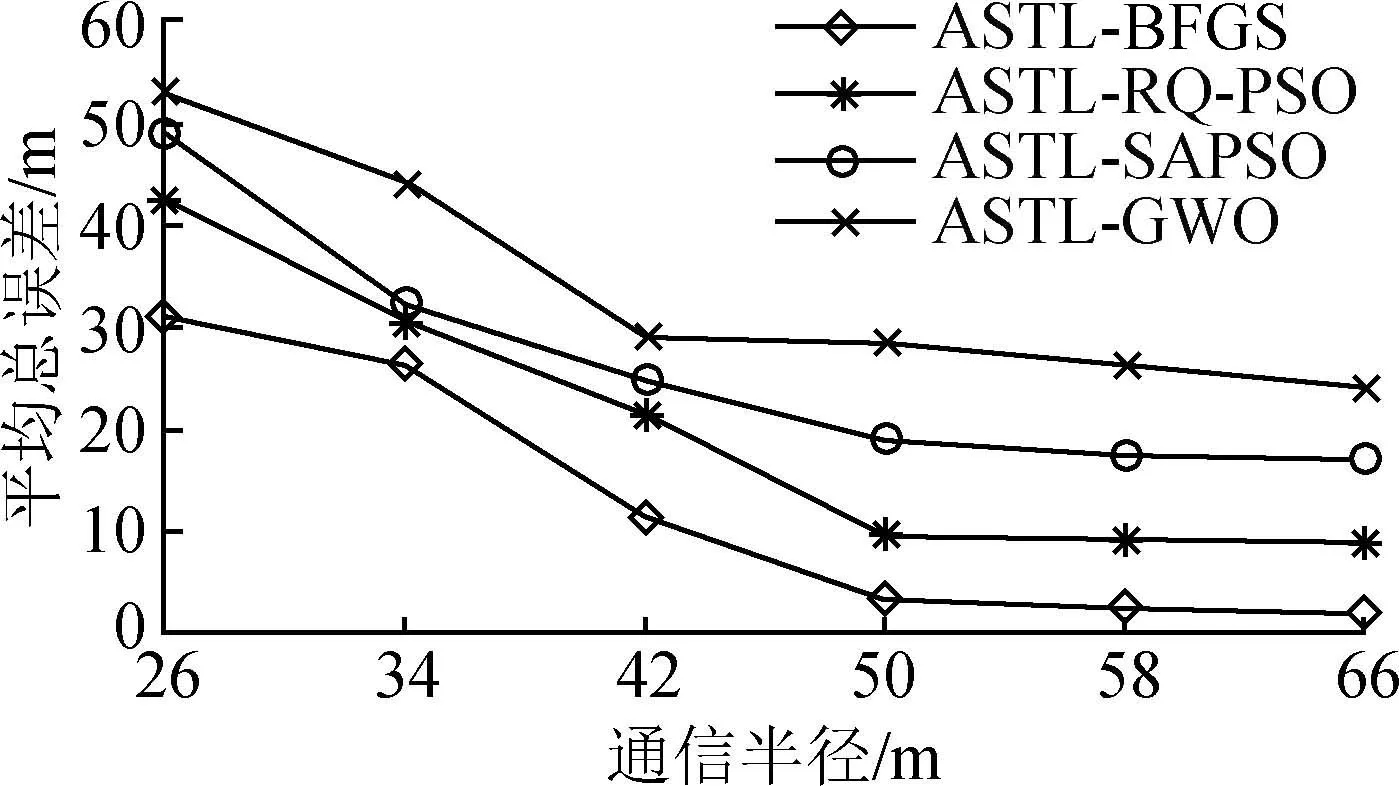
图11 平均总误差与通信半径关系

5 结 语

针对水下三维水声无线传感网络节点定位误差大的问题，提出一种基于高斯滤波和拟牛顿优化的水下定位优化算法；针对突发性环境噪声对测距结果的影响，提出对TL离线采样样本进行高斯滤波的方法，对所有的样本取加权平均，得到的值代入ASTL测距模型，达到了测距优化的目标，并采用BFGS算法对多边定位求得未知节点坐标的初始解进行优化，以降低定位误差。经仿真实验验证，本文提出的算法有效地降低了测距误差，提高了定位精度。