二次正交旋转组合设计优化花生秸秆微波裂解

罗朝阳，段军，何成奎，张平

（达州职业技术学院，四川 达州635001）

我国秸秆资源丰富，秸秆主要用作工业原料、生活燃料、土壤肥料以及畜牧饲料，虽然其用途广泛，但绝大部分还是成为了农业废物，大量的作物秸秆主要采取焚烧方式来处理，不仅污染环境，而且秸秆内部蕴藏的巨大额外价值也没有被利用[1]。对农作物秸秆的利用研究，不仅可以解决资源浪费的问题，还可以增加农民的收入，减少污染改善生态环境，为全球能源利用注入新的活力。对秸秆类农作物资源化利用的研究，成了较为热门的研究课题，Krieger-Biockett B等利用微波裂解对稻草秸秆、木质素等进行了研究[2-4]；万益琴等人利用微波裂解对玉米秸秆进行了研究，制备了生物质燃料[5]；熊佳定等研究了热过氧化氢预处理对花生秸秆酶解的影响[6]；华金玲等研究了花生秸秆与青贮玉米搭配对湖羊瘤胃发酵特性的影响[7]，为花生秸秆作为饲料应用提供了依据。国内外对微波裂解技术的应用已比较成熟，裂解对象却千差万别，但对花生秸秆的微波裂解制备生物质能源的研究较少，并且裂解条件尚需进一步优化。因此，实验选用花生秸秆作为研究对象，通过微波裂解将其裂解为固态、液态、气态三相产物，前期实验研究单因素（秸秆长度、裂解功率以及秸秆含水率）对三相产物产量的影响[8]，本实验以气体热值为因变量，利用二次正交旋转组合设计，找出最优的裂解条件并通过SPSS得出拟合方程、做统计分析，确定了最优的裂解条件。

1 实验部分

1.1 材料和仪器

花生秸秆（不含枝叶，含水率为8%），根据实验需要调节成含水率分别为18%、28%、38%；用剪刀和粉碎机（HCL-5型，北京华宏金诚有限公司）粉碎,筛网筛选得到不同尺寸的秸秆。

微波裂解装置（NJL4-2型，南京杰全微波设备有限公司）的裂解炉温度、功率可由操作界面进行控制。分析混合气体成分及含量采用气相色谱仪（Agilent Intuvo9000，美国安捷伦科技有限公司）。

1.2 实验条件

前期实验研究了裂解功率、秸秆长度和含水率对三相产率的影响，实验选择了1.5kW、2 kW、2.5 kW、3 kW四个功率水平进行裂解；然后选取1 cm、3 cm、粗粉粒径2 mm、细粉粒径60目等4个不同秸秆长度进行分析；采用8%、18%、28%、38%四个梯度的含水率进行研究，研究单因素对裂解混合气体热值和成分的影响。

本实验以混合气热值为因变量，采用二次正交旋转组合设计与星点设计（central composite design,CCD）相结合，通过SPSS等数据分析软件建立多种拟合方程[9]。其包括三部分:①中心点；②轴点；③二水平析因设计，即0、+1、-1、+λ、-λ，λ=F1/4，而F=k2（k为因素数，本实验k=3）。

2 结果与讨论

2.1 实验结果

在单因素实验结果的基础上，本实验以混合气热值为因变量，采用三因素五水平的二次正交旋转组合设计，星点设计如表1所示。

CCD表一般由三部分组成:①2k析因设计；②极值点:析因设计只适合线性拟合，因此，加上极值点便可适用于非线性拟合；③多次中心点重复试验。实验安排及结果如表2所示。

表1 星点设计

表2 二次正交旋转组合设计方案及结果

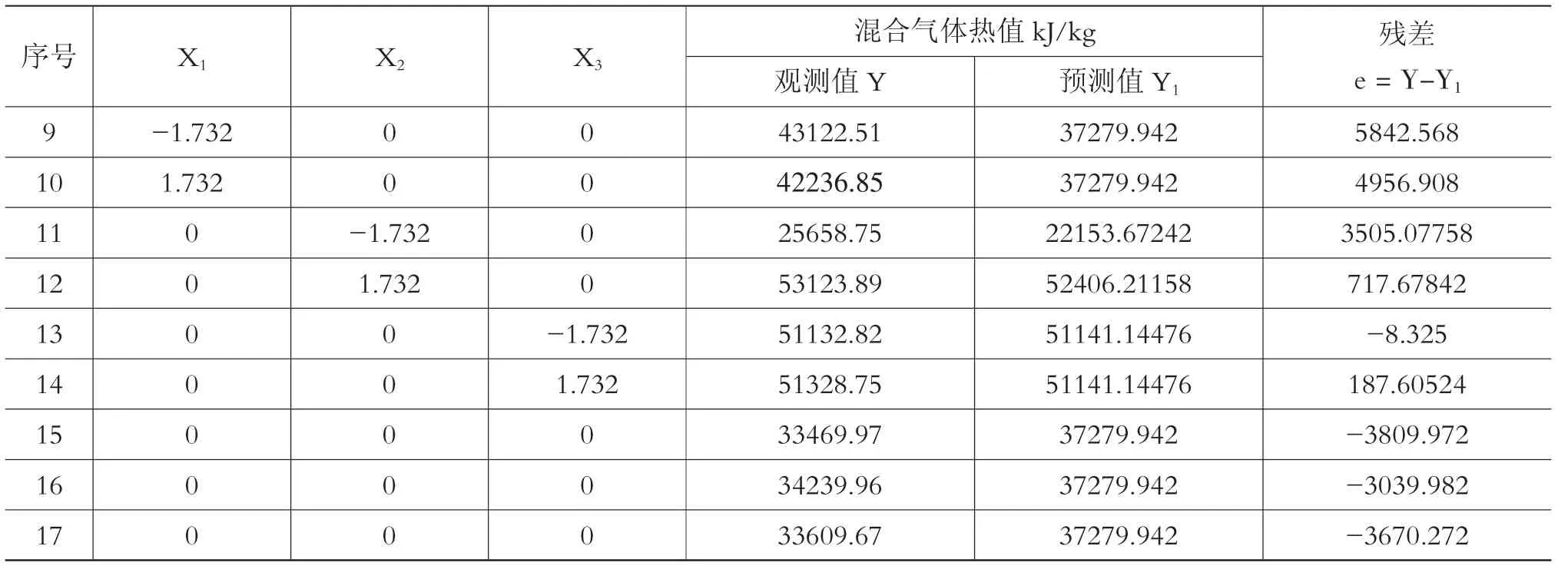
续表2

2.2 建立拟合方程

利用SPSS数据分析软件对表2数据进行分析，得到含水率、功率、长度与气相产物混合气热值的多元非线性拟合方程如下:

注:根据回归结果表3可以看出，由于存在多重共线性，X22被回归模型直接排除（容差为0，VIF无限大）。

根据表4、表5可看出，拟合方程的R2=0.923（R2反应因变量的全部变异能通过回归关系被自变量解释的比例，因此R2越大，则说明回归关系中可以解释的因变量的比例越大）,且P<0.05，由此说明，方程拟合较好，可信度较高。

经过对方程的系数分析，如表6可以看出，功率的一次项达到了极显著水平（P<0.01），长度的平方项、长度和功率的乘积项达到了显著水平（P<0.05），其他各项均无显著性差异。由于实验采用二次正交设计，所以可以直接去掉不显著项（α=0.05），简化方程如下所示:

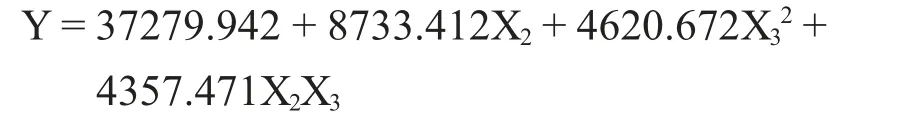
（注:方程中的自变量是按实验编码回归的，因此在预测其它热值时可按比例把对应编码找到，然后带入回归方程。）

将每组实验因素带入拟合方程，算出每组实验混合气热值的预测值及残差，表7为SPSS软件对残差和预测值的统计。

表3 已排除变量

表4 模型汇总

表5 失拟性分析

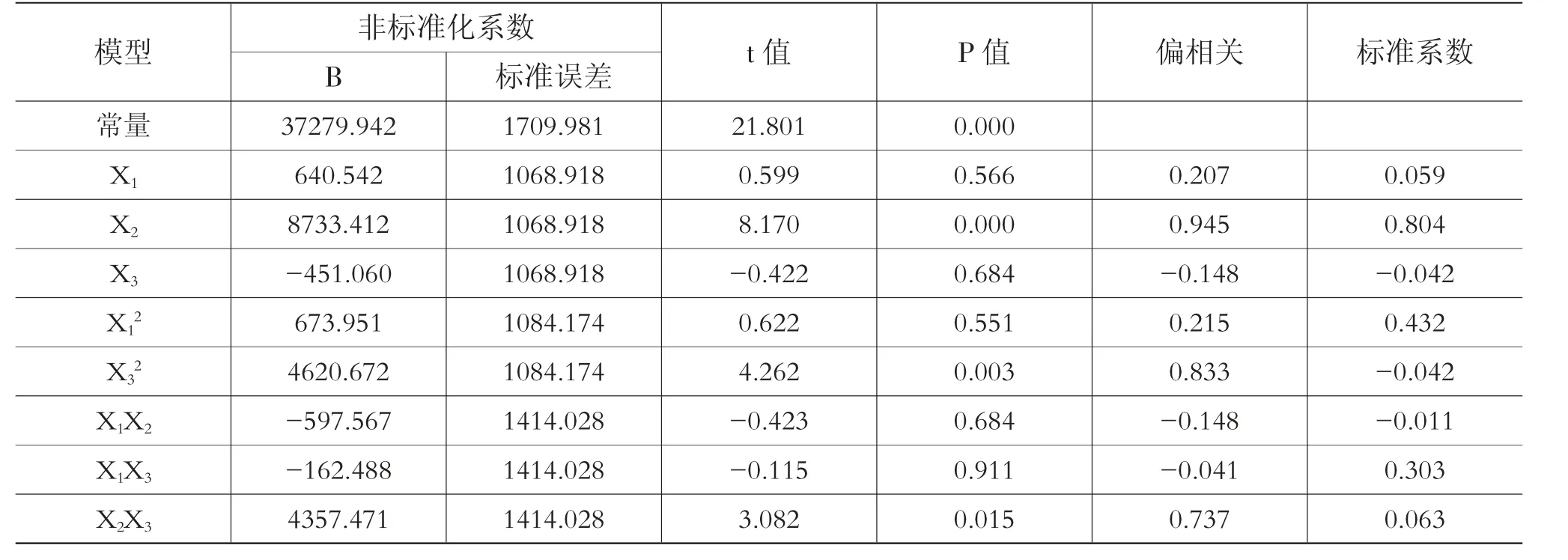
表6 系数分析表

表7 残差、预测值统计

2.3 主体间效应分析

利用方差分析，对主体间效应进行检验，如表8所示。在统计学中，反映一件事情发生的概率大小叫做P值，而每一个系数的P值则表示该系数所对应的因素对因变量的影响程度，P值越大，影响程度越小，也就是越不重要[10]。分析表8可得，所研究因素对混合气热值的影响程度从大到小依次为:功率>含水率>长度。所以，把握好这三个因素的合理取值范围以及考虑其相互影响，对提高混合气热值很有帮助。

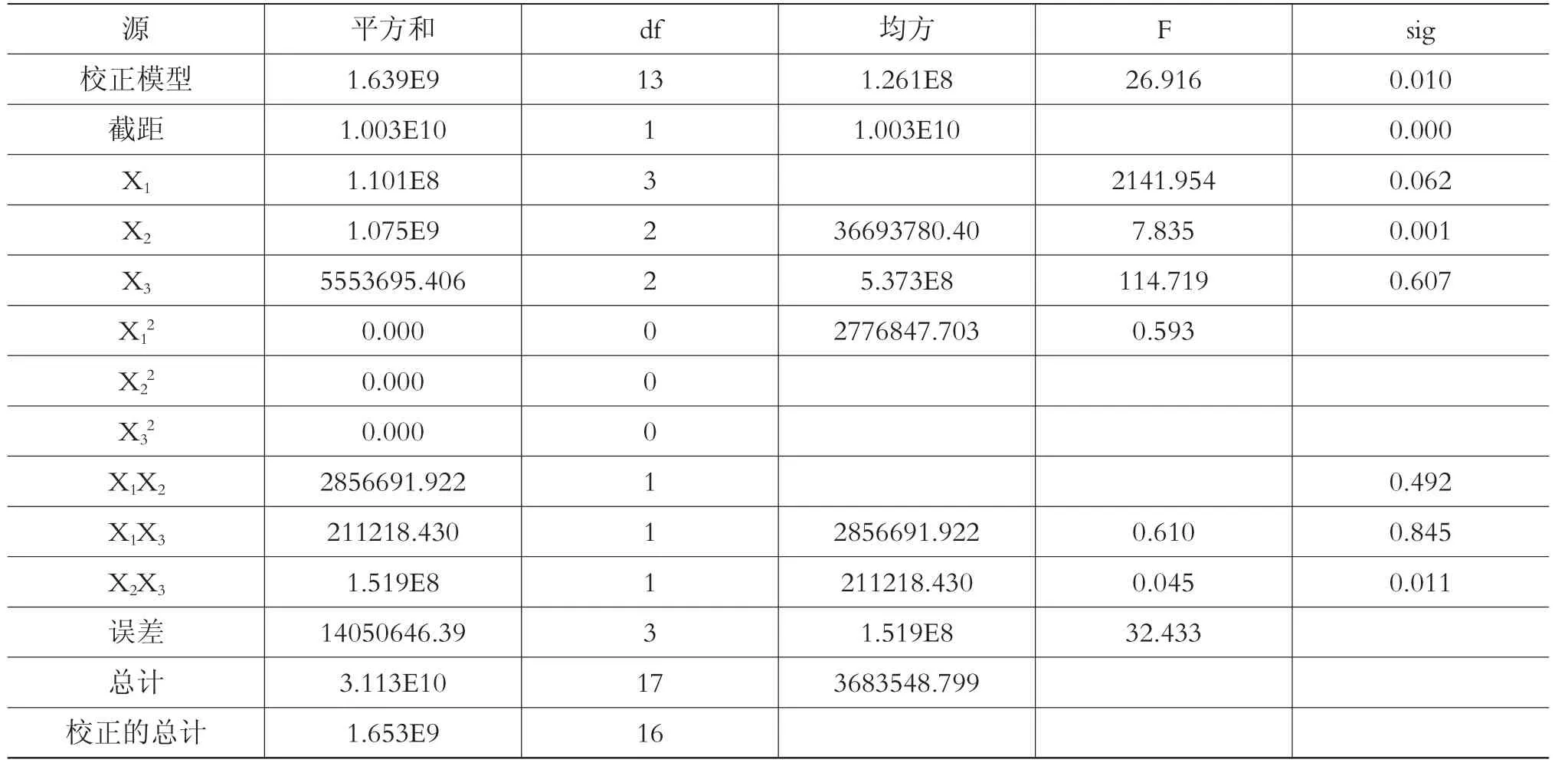
表8 主体间效应的检验

2.4 单因素效应分析

控制其中一个自变量不变，将其余自变量控制在0水平上，单独研究每一个自变量对混合气热值的影响，得到如下两个方程:

将各因素分别取-1.732，-1,0，1,1.732，依据上述方程，计算不同条件下混合气的热值，并绘制曲线，如图1所示。从图中可以看出，功率与混合气热值基本处于线性相关的关系，说明功率对混合气热值影响显著，且随着功率的增加，混合气热值会不断增加；而长度与混合气热值的曲线成抛物线形状，说明其影响没有功率显著。

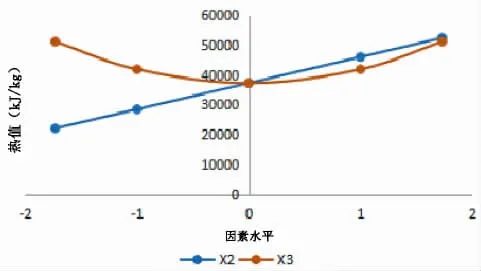
图1 含水率、功率对热值影响

2.5 双因素互作效应分析

从简化后的方程我们可以看出，X2和X3存在互作效应（见图2），因此，我们将X1固定在0水平，分析X2和X3对混合气热值的共同影响，即方程:

利用Excel的规划求解可以得出，自变量在-1.732～1.732的范围内，方程存在最大值和最小值，结果如表9所示。

图2 X2、X3对混合气热值互作效应

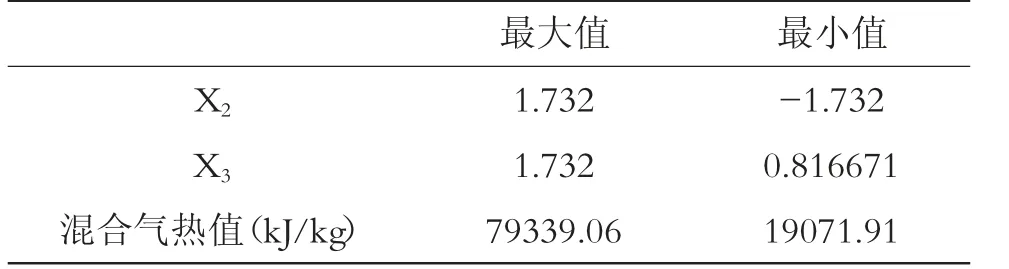
表9 最值结果

结果表明当裂解功率为2.5 kW、秸秆长度为5cm时，混合气热值最大为79339.06 kJ/kg；当裂解功率为1.5 kW、秸秆长度为3.9 cm时，混合气热值最小为19071.91 kJ/kg。

3 结论

（1）秸秆含水率对混合气热值影响不大；

（2）功率对热值的影响呈线性相关，随着裂解功率的增加，混合气热值不断升高；

（3）秸秆长度对混合气体热值的影响呈抛物线关系，综合整个拟合方程，最优解裂解条件为:裂解功率2.5 kW、秸秆长度5 cm。