基于频域特征波形模式匹配的故障诊断方法研究

焦卫东，丁祥满，严天宇，闫莹莹

（1.浙江省城市轨道交通智能运维技术与装备重点实验室；2.浙江师范大学工学院，浙江 金华321004）

滚动轴承是机械系统中的通用件，广泛应用于感应电机、轨道车辆走行部等旋转机械装备，其内圈、外圈、保持架以及滚动体元件极易发生疲劳破坏，导致突发的故障或非计划的生产停顿，造成严重的经济损失。机器健康状况监测中对轴承的监测相当重视，相应开发了多种诊断方法[1]。

任凌志等基于多尺度线调频基稀疏信号分解的广义解调方法，对非平稳故障信号进行平稳化处理，然后应用于非平稳转速下滚动轴承的故障诊断[2]。胡爱军等提出一种基于集成经验模态分解（EEMD）与峭度准则的包络解调方法。该方法基于最大峭度准则选取EEMD分解的本征模态函数（IMF），通过对IMF进行包络解调获得滚动轴承故障特征信息[3]。刘中磊等借助包络解调和线调频小波路径追踪算法，估计包络故障特征频率，通过角度重采样技术进行信号平稳化处理，然后利用双谱分析的对角切片进行轴承故障诊断[4]。刘丽娟等提出一种基于流形学习与一类支持向量机（SVM）的轴承早期故障识别方法，基于拉普拉斯特征映射流形学习算法用于样本特征压缩，一类支持向量机用于各状态的分类识别[5]。何青等针对滚动轴承发生故障时，振动信号的时域和频域特征都会发生变化的特点，提出了基于EEMD、改进果蝇优化算法和SVM的滚动轴承故障诊断方法[6]。史晓雪与吴亚锋提出了一种基于粒子滤波状态估计的滚动轴承故障识别方法，首先建立不同状态的自回归故障模型，再将正常模型转化为状态空间模型进而设计粒子滤波器，估计并提取故障残差相关特征，最后应用误差反向传播（BP）网络进行故障识别[7]。杨平与苏燕辰针对许多基于深度学习的滚动轴承故障诊断方法在小样本数据集下诊断性能下降的问题，提出一种基于卷积门控循环神经网络的轴承故障诊断模型，该模型在小训练样本情况下依然保持很高的故障识别准确率[8]。Shi等联合应用加窗分形维数变换以及广义信号解调技术，解决变转速下轴承诊断问题[9]。

本文提出一种基于频域特征波形模式匹配的故障诊断方法并应用于滚动轴承正常以及内圈、外圈、滚动体故障诊断中。该方法不需要复杂的特征提取，也不需要复杂的分类器设计。对比故障诊断结果表明，该方法在分类准确性与效率等方面具有明显的优势。

1 现有的滚动轴承故障诊断方法

无缺陷或故障的滚动轴承，理论上振动为零。当内、外圈或保持架、滚动体等元件缺陷或故障时，故障引起载荷变化进而造成滚动过程的非均匀性而以交变力形式作用于轴承，导致元件故障频率fd（及其高次谐波）对主轴旋转频率fr的幅值调制现象[10]。 元件故障频率fd=fbdfr，其中fbd为元件基础缺陷频率，包括过内圈频率fibd，过外圈频率fobd，保持架频率fcbd与滚动体自旋频率frbd，计算式如下

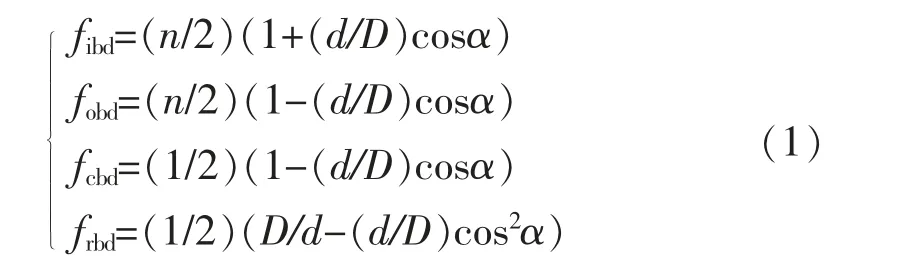
式中：n为轴承中滚动体数目；d为滚动体直径；D为轴承节径；α为滚动体接触角。

依据不同的诊断原理和所利用的信息，滚动轴承故障诊断方法可以归纳为基于故障特征频率分析的机理性诊断法和基于空间分集特征提取的模式识别诊断法两大类。

1.1 机理性诊断法

机理性诊断法以正向推理为主，该方法基于滚动轴承故障的幅值调制机理，通过分析振动调制信号获取故障特征频率，据此识别故障。此类方法认为故障信息主要集中于调制信号的包络中，通过包络解调和包络谱分析抽取故障的特征频率。但是，变转速工况以及故障的内在特性往往导致轴承的非平稳振动，此时以快速傅里叶变换（FFT）为基础的传统包络谱分析将失效，难以获得准确的故障特征频率。针对此问题，出现多种信号平稳化处理算法，相应地形成多种滚动轴承故障机理性诊断法[2-4]。

假设多分量非平稳信号x（t）的模型为

式中：fi（t）与φi（t）分别为频率函数与相位函数。

采用以下多尺度线调频基稀疏信号分解求解φi（t），据此进行广义解调以抽取故障特征频率[2]

式中：D（·）为基元函数库；haμ，bμ，I（t）为多尺度线调频基元函数；I为动态分析段且I=[kN2-j～（k+1）N2-j]；j为分析出度系数且j=0，1，…，log2（N－1）；N为采样长度，k=0，1，…，2j－1；Kaμ，bμ，I为归一化系数，使得‖haμ，bμ，I‖=1；aμ为频率偏置系数；bμ为频率斜率；WI（t）为矩形窗函数，当t∈I时为1，当t∉I时为0。

基于线调频基稀疏信号分解得到的故障特征频率估计，可以进一步用于非平稳信号插值和角度重采样处理，以达到信号平稳化处理目的，然后利用如下的双谱分析进行轴承故障诊断[4]

式中：Bxx（·）为双谱函数；ω1，ω2表示频率变量；Rxx（·）为自相关函数；τ1，τ2表示时移变量。

采用可抑制传统EMD模态混叠的EEMD算法执行信号分解，分解过程本质上也是一个信号平稳化处理过程。然后，基于峭度最大化准则选取包含最多故障信息的IMF，再通过包络解调抽取故障特征频率[3]。

轴系偏心、变形、轴承异常磨损、轴承（座孔）加工或安装误差以及异常工况导致的外载荷变化或润滑冲击，均可引起轴承的异常振动。此外，滚动轴承中包括许多刚性较差的结构（如保持架等），往往会在振动调制信号中引入复杂的非线性振动[11]。一般滚动体和内外圈之间存在1%～2%转频的滑动[12]，传动误差、杂质或异物堵塞等因素也会造成实测故障频率和理论故障频率之间的误差[13]。此类方法对轴承故障诊断的有效性严重依赖于诊断者的专业技术水平，在实际应用中往往面临困难。

1.2 模式识别诊断法

模式识别诊断法以反向推理为主，该方法基于机器学习理论，通过监督或半监督式学习获得模式分离超平面，据此识别未知故障模式。对于此类方法，利用已知模式类的（类标）训练样本提取具有空间分集特性的量化特征是关键，而据此设计合适的模式分类器则是核心。基于不同的特征提取与/或模式分类算法，相应地形成多种滚动轴承故障模式识别诊断法[5-8]。

有效的量化特征提取，必须建立在以故障机理为基础的征兆关联特性研究上。针对某些时域参数对早期故障比较敏感的特点，以时域参数作为原始特征，再利用流形学习方法融合压缩生成敏感特征[5]；针对轴承故障振动信号或过程的非平稳性，对EEMD分解产生的IMF提取均方根值和重心频率等时域特征[6]，或者基于正常过程的自回归模型设计粒子滤波器以提取不同故障状态的残差相关特征，然后应用BP神经网络进行故障模式的分类[7]；也有采用两级卷积门控循环网络，一体化实现故障过程的高层时序特征提取与故障模式的分类识别[8]。

一类支持向量机本质上是寻找一个能够包含全部正类样本（如正常状态）的最小超球体，其优化准则表达如下[5]

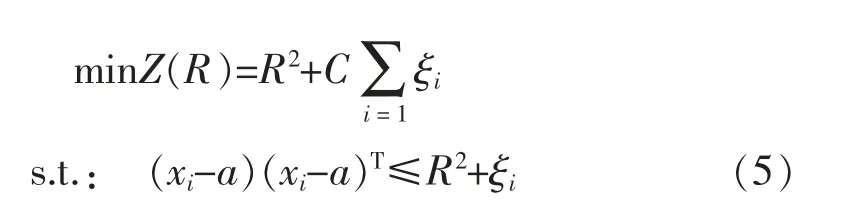
式中：Z（·）为准则函数；xi为第i个正类样本；R为最小超球体半径；a为球心；C为惩罚系数；ξi为松弛变量且ξi≥0，i=1，2，…，N。

由于惩罚参数C和核函数参数σ对SVM分类器性能具有关键影响，何青与褚东亮等引入如下的可变步长以取代传统果蝇优化算法中的固定步长L进行SVM参数优化

式中：L0为初始步长值；Imax为最大觅食迭代数；I为当前觅食迭代数；L为递减步长值。

基于时域特征提取的SVM基模式识别诊断法虽然适用于小样本模式分类问题[5-6]，但是在如式（6）所示的SVM算法参数优化过程中又引入了L0与Imax等新的参数，它们的选择需要依靠经验；此外，流形学习特征维压缩算法的维数参数d、粒子滤波器设计所需的故障过程时序建模参数以及BP网络、卷积门控循环网络参数等[7-8]，往往也需要依赖个人经验进行设置，严重影响了这些算法的实际应用。

2 频域特征匹配方法

式中：S1，S2与S3分别为A与B的余弦，相关和互信息相似度；θAB为A与B之间的夹角，且有0≤θAB≤π/2；ρAB为A与B之间的皮尔逊相关系数；E（·）为数学期望；μ与σ分别为均值和标准差。IAB为A与B之间的归一化互信息；H（·）与H（·，·）分别为边缘熵和联合熵。显然，S1，S2与S3满足0≤S1，S2，S3≤1，作为信号相似程度评价指标，将在随后的滚动轴承故障诊断中具体应用。

3 实验研究

实验数据来自美国凯斯西储大学（CWRU）轴承数据中心，该数据采集自如图1所示的滚动轴承故障模拟实验装置。该装置配备有一台2 hp电动机（左边），一个扭矩编码器（中间），一个功率测试计（右边）以及电子控制器。电机主轴分别由驱动端和风扇端轴承支承，单点损伤缺陷采用电火花加工方式分别引入两端轴承的内圈，外圈和滚动体，连同正常状态一起形成四种模式。选取风扇端转速为1 750 r/min，损伤尺寸为0.177 8 mm（0.007 inch）的故障模拟数据，对应早期的微弱故障，包括驱动端（D）和风扇端（F）两个测点的垂向振动观测信号，信号采样频率为12 kHz[17]。

图1 滚动轴承故障模拟实验台[17]Fig.1 Test rig for fault simulation on rolling element bearings［17］

以D测点的正常（C1:np）和内圈故障（C2:fi）振动信号为例，其FFT幅值谱波形如图2所示。

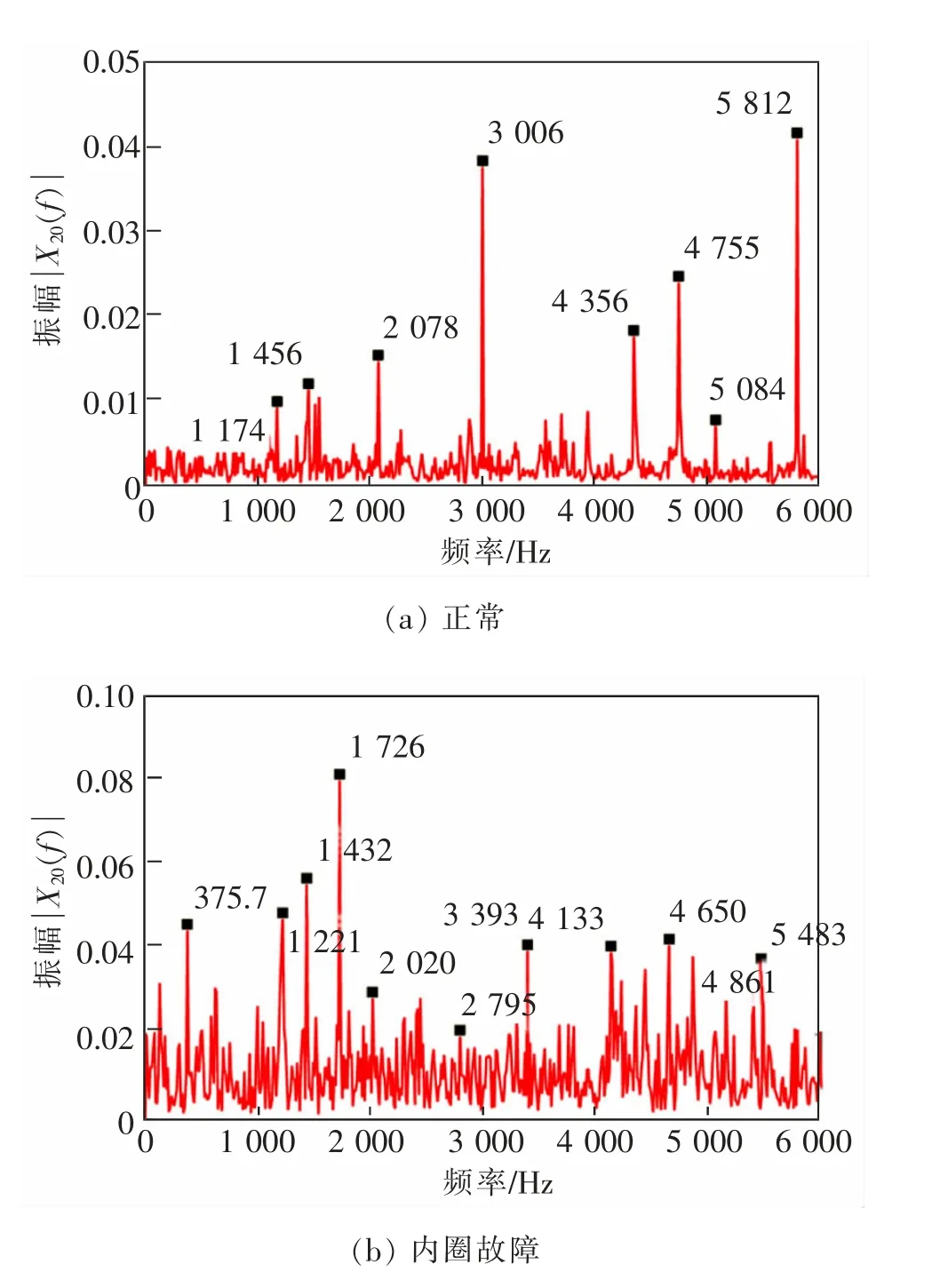
图2 不同模式类D测点振动信号的FFT幅值谱波形Fig.2 FFT-based amplitude spectral waveforms of vibration signals in Position D belonging to different patterns

风扇端轴承0.177 8 mm（0.007 inch）级别的损伤使用瑞典的斯凯孚（SKF）轴承进行模拟，内圈、外圈与滚动体元件的基础缺陷频率分别为fibd=4.946 9，fobd=3.053 0与frbd=3.987 4 Hz[17]。驱动端与风扇端轴承的滚动体个数分别为n0=9与n1=8。经过计算，主轴旋转频率fr=1 750/60=29.17 Hz，驱动端与风扇端轴承滚动频率分别为f0=n0fr=262.50与f1=n1fr=233.33 Hz， 元件故障 频率fd=[fdi，fdo，fdr]=[fibd，fobd,frbd]fr=[144.29，89.05，116.30]Hz。根据滚动轴承的振动调制机理，振动频谱中应该包含有fr，f0，f1及其高次谐波以及mfdi±kfr，mfdo±kfr，mfdr±kfr；m=1，2，…；k=1，2，…等幅值调制频率成分[10]。但是，滚动轴承振动的非线性与非平稳性，导致许多与结构共振相关的、难以解释的异常频率成分出现，见图2。从不同模式类FFT幅值谱中无法获得有意义的故障特征频率信息，即使在正常状态谱图（图2（a））中也不能清楚地观察到主轴旋转频率、驱动端与风扇端轴承滚动频率fr，f0与f1等频率分量。直接对滚动轴承故障振动信号进行FFT分析是无效的，这也是滚动轴承机理性诊断法[2-4]中采用振动或共振解调的根本原因。不过，随后将会看到：从FFT幅值谱中虽然不能有效抽取滚动轴承元件的故障特征频率，但是并不影响本文所建议方法的应用和效果。

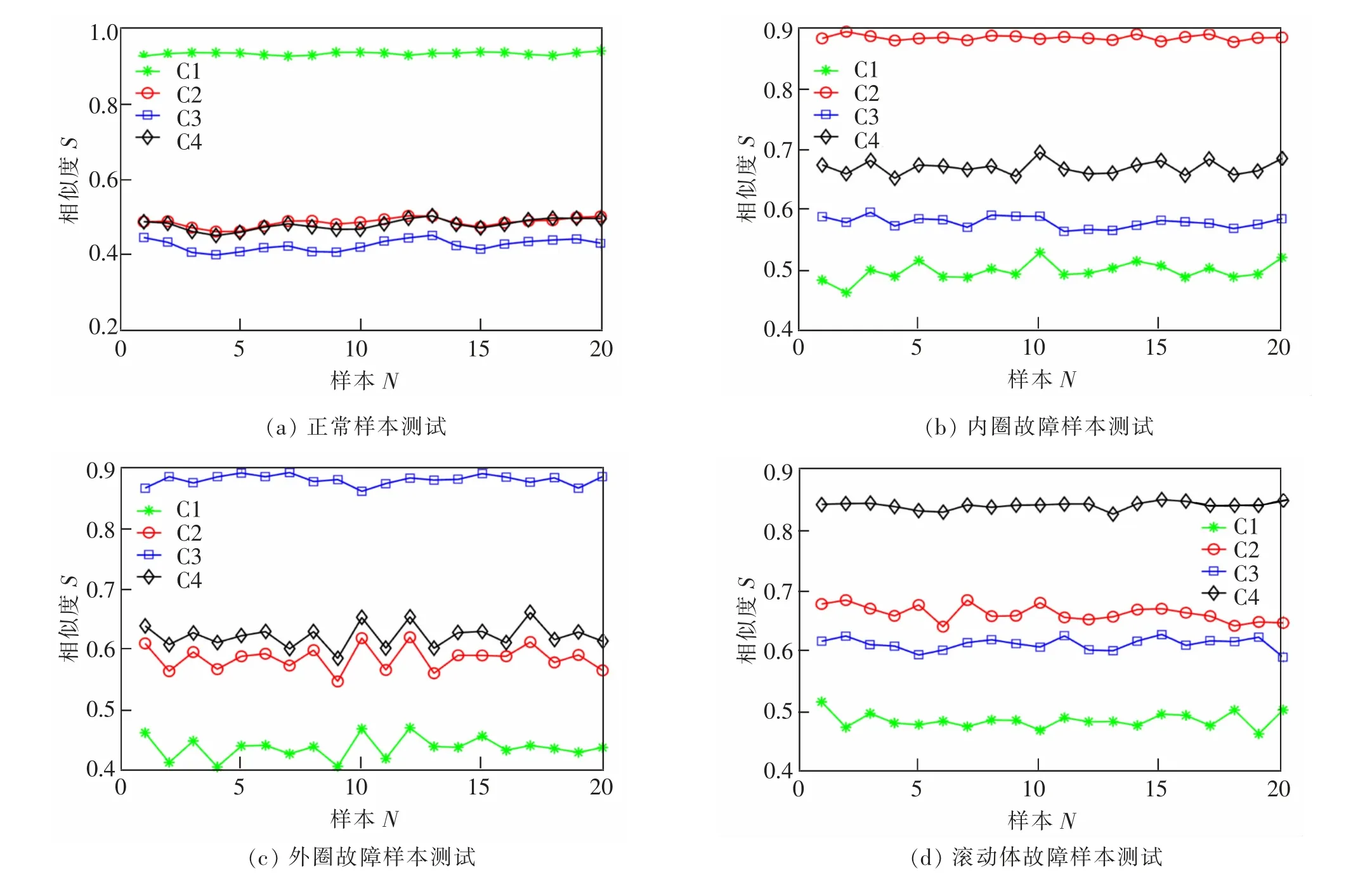
图3 基于余弦相似度指标S1的D测点振动幅值谱特征波形模式匹配结果Fig.3 Pattern matching based on cosine similarity index S1 using vibration amplitude spectra in Position D

从4种模式各100个FFT幅值谱特征波形样本中任取80个样本构成训练集，另外20个样本构成测试集，分别依据式（8）～式（10）给出的3个相似度指标执行频域特征匹配。基于余弦相似度指标S1、相关相似度指标S2和互信息相似度指标S3的D测点振动幅值谱特征波形模式匹配结果如图3，图4和图5所示。

如图3（a），当使用正常（C1:np）测试集样本进行测试时，所有20个测试样本对正常（C1:np）训练集的余弦相似度均达到最大。对内圈故障（C2:fi）、外圈故障（C3:fo）、滚动体故障（C4:fr）3类测试集样本进行模式匹配也获得了相似的结果，即当测试样本所属模式类与训练集样本相同时相似度达到最大值，如图3（b）、图3（c）与图3（d）所示。如图4与图5所示，当使用相关相似度指标S2与互信息相似度指标S3进行模式匹配时，所得结果类似。

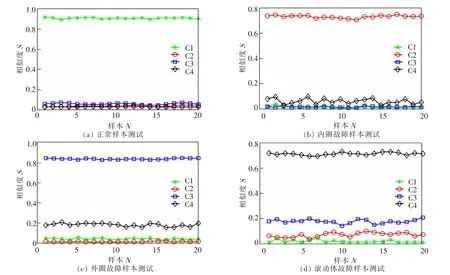
图4 基于相关相似度指标S2的D测点振动幅值谱特征波形模式匹配结果Fig.4 Pattern matching based on correlation similarity index S2 using vibration amplitude spectra in Position D

图5 基于互信息相似度指标S3的D测点振动幅值谱特征波形模式匹配结果Fig.5 Pattern matching based on mutual information similarity index S3 using vibration amplitude spectra in Position D

在表1中，进一步归纳了对D和F两个测点的振动幅值谱特征波形应用余弦相似度指标S1进行模式匹配所获得的相似度数据的统计特征。在表1中，μ与σ分别为平均值与标准差。可以看到，当测试样本与训练样本所属模式类相同时，相似度平均值达到最大，见表中粗体部分。对于D测点振动幅值谱特征波形模式匹配，最大相似度S1的平均值分别为0.922 3（C1-C1），0.866 5（C2-C2），0.897 5（C3-C3）与0.856 7（C4-C4）；对于F测点振动幅值谱特征波形模式匹配，最大相似度S1的平均值分别为0.922 3（C1-C1），0.866 5（C2-C2），0.897 5（C3-C3）与0.856 7（C4-C4）。

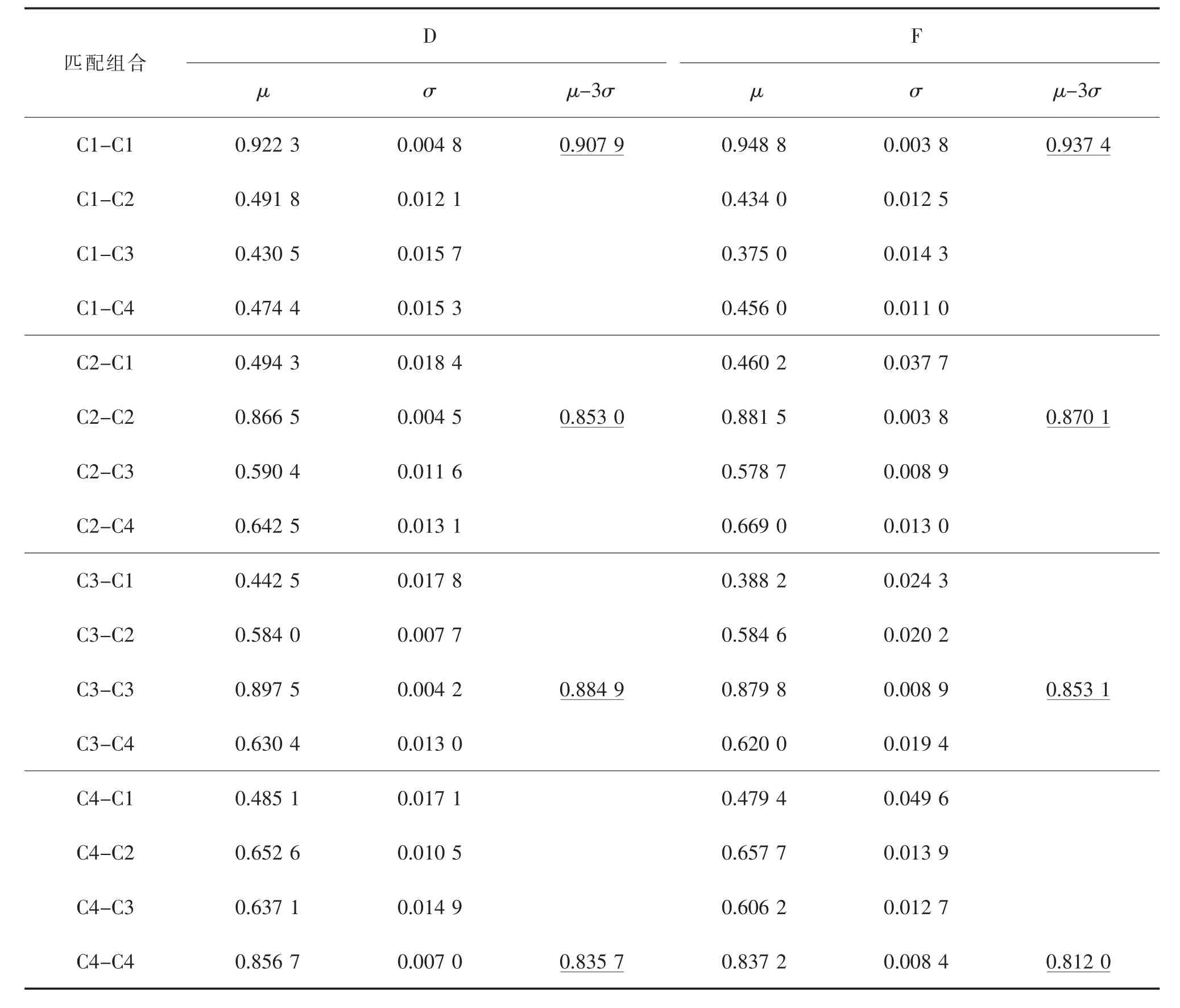
表1 基于S1相似度指标模式匹配数据的统计分析（包括D和F测点）Tab.1 Statistics of pattern matching data based on S1 similarity index(including D and F directions)

依据概率学理论，正态分布数据在区间[μ-3σ,μ+3σ]的分布概率为0.997 3，这就是众所周知的3σ准则[18]。假设振动幅值谱特征波形模式匹配所获得的相似度数据服从正态分布，可以借鉴3σ准则进一步确定用于滚动轴承故障模式分类的特征相似度阈值。在表1中，以下划线分别给出了4个模式类正确匹配时最大相似度正态分布区间的下限值μ-3σ，即0.907 9，0.853 0，0.884 9，0.835 7（D测点）以及0.937 4，0.870 1，0.853 1，0.812 0（F测点），据此估计特征相似度阈值分别为0.82（D测点）与0.80（F测点）。由于阈值估计时向下预留了一定的安全余量，因此预期能够获得准确的模式分类结果。

表2对比给出了本文所建议方法与一些典型模式识别诊断法对CWRU轴承故障的分类性能。

表2故障诊断方法性能比较（D测点）Tab.2 Performance comparison on different fault classification approaches(Position D)

由表2可见，本文所建议的方法对未知的滚动轴承故障模式实现了完全准确分类，其分类效果优于文献[5，7-8]所给出的方法。此外，对于包含80个训练样本的训练集，全部20个测试样本的模式匹配耗时不超过2 s。考虑到FFT算法的高运算效率，而且整个分类过程不需要其他繁琐的特征提取与复杂的模式分类器设计环节，基于频域特征波形模式匹配的滚动轴承故障诊断方法具有明显的高效率、高精度优势，对于在线的自动故障分类应用具有重要的价值和意义。

4 结论

1）对属于不同模式类的、在不同测点的滚动轴承振动观测数据进行FFT分析，以获得相应的幅值谱数据。不需要复杂的特征提取，直接由幅值谱特征波形构建训练集，并依据统计学原理估计用于故障模式分类的特征相似度阈值；对于待分模式类，由其振动观测数据经过FFT分析生成幅值谱特征波形测试样本；不需要设计神经网络、支持向量机等复杂的分类器，仅仅依据简单的相似度评价指标，通过与训练集样本进行频域特征波形模式匹配并与特征相似度阈值进行比较，即可高效实现准确的模式分类。

2）本文诊断案例中，对于正常、内圈故障、外圈故障以及滚动体故障4个模式类，无论是应用D测点还是F测点的振动数据，当测试样本所属模式类与训练样本相同时相似度（S1，S2或S3）达到最大值，其值均大于0.8，0.67或0.08（用不同的相似度指标获得的分类阈值也不同）。本文所建议的方法对训练集容量要求低，适于解决小样本分类问题。此外，通常情况下初建的故障诊断特征模板库往往是不完备的。本方法在实际应用中，如果某未知的待分模式类样本与特征模板库中所有训练集样本的S1，S2或S3相似度均明显小于0.8，0.67或0.08，则可以认为该测试样本不属于模板库中的任何模式类，将作为一个新类并入现有的诊断特征模板库中，这从另一方面体现了本文所建议的频域特征波形模式匹配方法具有很强的自学习能力。

3）由于结构刚度差异较大，加之变速运行工况以及故障内在特性的影响，滚动轴承振动具有明显的非线性和非平稳性。此时，直接应用FFT基谱分析难以抽取有意义的故障特征频率。除去刚度和工况等客观因素，滚动轴承的振动特性与故障特性关系密切。尽管FFT幅值谱中与故障相关的特征频率信息已经发生了严重畸变，但是具有一定的畸变规律，与故障的内在特性密切相关，并且隐藏于FFT幅值谱波形中。基于频域特征波形模式匹配的故障诊断可以全面地利用故障特征信息，取得最佳的故障诊断效果。当然，从机理性诊断研究的角度，未来有必要加强滚动轴承机械动力学建模与分析，深入探索FFT幅值谱中故障特征频率信息畸变的内在机理或规律。