动车组的多变量非线性预测控制研究
2021-06-18李中奇
耿 睿,李中奇,杨 辉
(华东交通大学1.电气与自动化工程学院;2.江西省先进控制与优化重点实验室,江西 南昌330013)
高速列车具有速度快、准时、能耗利用率较高等优点,其中高速动车组包括牵引、制动和惰行等运行工况。研究高速列车动车组的实时精确速度控制问题,对于实现高速列车自动驾驶具有重要的应用价值,也是未来高速列车自动驾驶算法的核心问题[1]。
针对高速动车组运行过程中的建模问题,袁海军[2]对高速列车进行动力学分析,通过单质点模型建立了特征模型,提出了最优PID控制器,对速度曲线进行了跟踪。连文博[3]基于单质点模型建立了高速列车的状态空间方程,通过对传统PID控制器的改进,将高速列车受干扰最为扩张状态设计自抗扰控制器,并证明了算法的可行且具有抗干扰性强、追踪误差小的优点。刘晓宇[4]通过分析高速列车制动控制过程,建立列车制动过程的传递函数模型,反映了控制力产生的动态过程,实验表明了模型的准确性。上述文献均通过对高速列车动力学分析建立了单质点模型,但实际中动车组列车均采用了动力分散配置,单质点模型不足以描述动车组各动力车厢的牵引或制动力的分配情况。李中奇[5-6]通过分析单个车厢的受力情况以及制动过程的特点,将速度和制动力的传递函数模型与单个车厢的动力学模型相结合,提出了动车组的多质点模型。衷路生[7]通过对列车长度以及对每节车厢的受力进行深入分析建立了高速列车的多质点模型,有效的解决了列车通过变坡点和变曲率点时的速度跳变问题。S ong[8]将车厢间的耦合力看作列车内力,采用单一坐标模型系统来描述列车系统的位移和速度,将多维模型转化为一维模型,简化了列车内部的受力情况。Lin[9]通过分析列车车钩耦合力,将车钩建模为非线性弹簧跟阻尼器的组合,通过分析高速列车的运行阻力、外界干扰以及建模不确定性因素建立了高速列车的多质点模型。
针对动车组运行过程中的控制问题,传统的PID控制在参数选择上依赖人工选取,PID参数往往整定不良,性能欠佳,不利于动车组安全舒适运行。而广义预测控制将模型与参数估计相结合,对于动车组运行过程中参数时变的问题,易于在线估计参数,同时在发生参数突变问题时,广义预测控制具备自适应调节能力,可以维持原控制性能不变。李中奇[10]设计了基于极限学习机的广义预测控制方法,将模型参数通过极限学习机神经网络直接估计控制器系数,减少了计算量,同时算法具有良好的跟踪能力。李中奇[11]采用双自适应广义预测控制方法,不仅实时更新模型参数而且实时更新控制器参数,实现了动车组制动过程对目标速度的精确跟踪。
高速动车组实际运行过程中会受到非线性空气阻力、强风、雨雪天气等的影响,具有很强的非线性,在面对非线性问题中,戈萌[12]针对高速列车运行过程中存在的输入非线性、非线性空气阻力、未知的外部扰动以及执行器故障问题,设计了一种分数阶有限时间控制器实现了高速列车对于目标曲线的高精度跟踪控制。贾超[13]通过分析车间耦合力、非线性阻力、列车运行状态,建立了非线性多质点模型,并且考虑了多优化目标及运行约束条件等问题,提出了高速列车的非线性模型预测控制。
针对上述问题,在建模方面通过分析牵引制动系统的构成,以及动车组采用动力分散式驱动并由多个动力车厢组成的特点,建立了动车组的多动力单元模型,并将非线性空气阻力、未知扰动等描述为未建模动态项,通过BP神经网络实时估计。在控制器设计中,设计了非线性广义预测控制器并结合动车组现场运行数据进行仿真,验证了该方法的有效性。
1 动车组的多动力单元模型
动车组是由若干带有动力的机车与不带动力的拖车编组而成,我国现有CRH380A型动车组,动力编组形式为6动2拖;目前我国高速动车组的牵引动力形式可分为分布式动力结构和集中式动力结构两种类型;随着高速动车组运行速度的不断提升,动力集中式动车组受到轮轨粘着和功率等因素的限制,缺点暴露无遗,而分布式动力结构将动力分置于每节车辆或大部分车辆中,牵引制动的性能有着明显的改进。
1.1 牵引-制动系统
分析动车组的牵引-制动系统可知,当司机或ATO装置发送控制指令,各动车的牵引/制动控制单元接收传送的控制指令,计算出相应时刻所需的牵引/制动力。
牵引阶段,从控制指令的发出,到动车组启动加速,存在着系统延时;当动车组开始加速,牵引加速度缓慢增长至所需要的目标加速度。
制动阶段,目前高速列车在制动阶段采取电制动与空气制动相结合的形式,在动车组运行速度较快时,动车组采用电制动方式,当动车组运行速度较低时,由于电机转速较慢不足以提供所需制动力,此时动车组采用电制动与空气制动相结合的方式,考虑到空气制动多出现在动车组速度较低时且延时大计算繁琐,本文制动阶段只考虑电制动。当动车收到制动信号,因系统存在传输延时环节,动车组在延时后开始制动;动车组减速度逐步变化至目标减速度。
牵引-制动控制系统流程图如图1所示。

图1 控制系统工作流程图Fig.1 Flow chart of control system
1.2 动力学模型
当控制单元接收ATO或司机发出的控制指令时,由于网络和物理传输延时的存在,经过短暂周期后作用于动车上,此过程可用一阶动态系统近似描述[14]

式中:a(t)为控制加速度,通过控制器作用产生的加速度;a(t)为目标加速度;τ为系统响应时间常数;T为延时时间常数;上述公式反映了牵引/制动力产生的动态过程。复频域可表示为
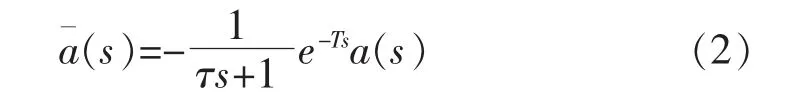
动车组的实际加速度a1(t)由控制加速度以及非线性空气阻力引起的加速度d构成

建立以目标加速度为输入,实际速度为输出的动车组模型,如图2所示。

图2 动车组控制模型Fig.2 EMU control model
图2传递函数如下所示
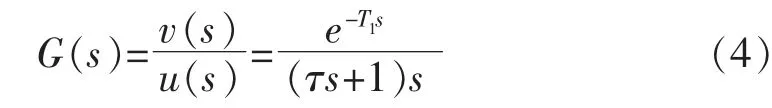
采用帕德方法近似延时环节,并利用双线性变换将上述传递函数离散化可得

考虑到CRH380A动车组编组形式为6动2拖,且牵引系统包括T1+M1+M2,M3+M4,M5+M6+T2组成3个独立的牵引动力单元,因此我们将高速列车分为3个动力单元,且每个动力单元均可实现牵引-制动环节;第1个动力单元为T1+M1+M2;第2个动力单元为M3+M4;第3个动力单元为M5+M6+T2如图3所示。

图3 CRH380A型动车组动力单元分布图Fig.3 Power unit distribution of CRH380A EMU
由式(5)可得动车组的多动力单元线性模型为

式中:A(z-1)=I+A1z-1+A2z-2+A3z-3;B(z-1)=B0+B1z-1+B2z-2;V(k)=[v1(k),v2(k),v3(k)];U(k)=[u1(k),u2(k),u3(k)];分别为每个动力单元的输出速度以及输入目标加速度;A(z-1)和B(z-1)均为关于z-1的3×3对角多项式矩阵。
考虑到上述线性模型未考虑非线性空气阻力的影响,随着速度的增加,空气阻力的非线性越来越强,在此我们将线性模型与实际列车模型的误差定义为未建模动态项,结合式(6),动车组的运行模型可描述为线性模型(6)与未建模动态项组成的集成模型

其中,ξ(k)=[ξ1(k),ξ2(k),ξ3(k)]为每个动力单元的未建模动态项。
2 参数估计
考虑到模型参数的缓慢变化,利用BP神经网络实时估计系统未建模动态项,利用递推算法实时估计系统模型参数,从而改善高速列车自动驾驶的控制精度。
2.1 BP机神经网络
BP神经网络具有很强的非线性映射能力,因此可以用来估计系统中的非线性未建模动态项,其数学模型为

其估计值为ξ(k),且与系统过去时间的输入输出相关;z(k)=[vi(k-1),…,vi(k-3),ui(k-1),…,ui(k-3)]为神经网络的输入;W,V为表示神经网络的权值矩阵;μ1,μ2为阈值;s(·)为sigmoid算子,通过反向传播不断修改阈值和权值,使得输出最优。
2.2 模型参数更新策略
由式(7)可以得到动车组集成模型的参数辨识方程为

式中:xi(k-1)=[-vi(k-1),…,-vi(k-na),ui(k-1),…,ui(k-3)];θi=[ai1,…,ai3,bi0,…,bi2]。
利用BP神经网络实时估计系统未建模动态项,得到估计模型为

其中θ˙i(k)为第i个动力单元k时刻参数θi(k)的估计值,其辨识算法如下所示[15]

式中:Δ为已知的误差最大值;e(k)=w(k)-v˙i(k);w(k)为已知速度曲线。
3 多变量非线性广义预测控制方法
基于上文线性模型与非线性未建模动态组成的集成模型提出多变量非线性广义预测控制方法如图4所示,控制器由反馈控制器以及未建模动态补偿器两部分组成,反馈控制器用来控制模型输入跟踪参考速度曲线;非线性未建模动态补偿器用来消除非线性项对于闭环系统的影响。

图4 多变量非线性广义预测控制器Fig.4 Multivariable nonlinear generalized predictive controller
3.1 控制器设计
引入如下预测控制性能指标[16]

式中:Rj和λj为对角加权矩阵;Sj为关于z-1的对角加权多项式矩阵;N和Nu分别为预测时域长度和控制时域长度。为获得j步超前预测,引入Diophantine方程

式中:Ej(z-1),Fj(z-1),Gj(z-1),Hj(z-1)均是关于z-1的对角多项式矩阵,由式(7),式(13),式(14)可得J步输出预报

将式(15)带入上式性能指标中,并且选择适当的加权多项式矩阵Lj(z-1)使得[Ej(z-1)+Sj(z-1)]ξ(k+j-1)=Lj(z-1)ξ(k-1),这 里Lj(z-1)=Lj,0+Lj,1z-1+…+Lj,n1z-n1)是关于z-1的对角多项式矩阵,将式(15)带入式(12)中可得

将式(16)化为矩阵形式

令矩阵(G QG+λ)-1G Q的前3行为:P=[P1,…,PN],则多变量预测控制律方程为

3.2 控制器参数选择
将式(19)代入式(7)中可得
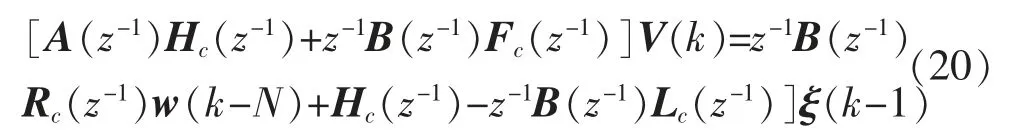
由上述公式可知[Hc(z-1)-z-1B(z-1)Lc(z-1)]ξ(t-1)含有非线性未建模动态项,为了消除未建模动态项对系统的影响,选择适当的加权矩阵Sj(z-1),(Sj(z-1)与Lj(z-1)相关)使得下式成立

选取多项式矩阵使得下式成立

消除系统的稳态跟踪误差。
综上,多变量非线性预测控制算法的步骤如下:
步骤1测量动车组每个单元的速度输出v(k);
步骤2利用极限学习机神经网络估计未建模动态项;
步骤3利用辨识算法实时估计动车组各动力单元参数;
步骤4利用辨识后的参数求解Diophantine方程;
步骤5利用式(18),式(19)求解所需控制率;
步骤6选择相应的加权多项式Lj(z-1),qj,λj;
步骤7将所得控制输入带入模型并得到新的输出。
4 仿真试验分析
为验证文章中所提到的建模方法以及控制方法的有效性,本次仿真实验我们采取了动车组在京沪铁路上从济南到徐州东区间的运行数据进行仿真试验。考虑到牵引、制动工况下延时不一致,且每个动力单元的系统传输延时不同,在牵引工况下,动力单元1的系统响应时间τ1为0.4 s;传输延时T1为1 s;动力单元2的系统响应时间为τ2为0.4 s;传输延时T2为1.1 s;动力单元3的系统响应时间为τ3为0.4 s;传输延时T3为1.2 s;在制动工况下,系统的响应时间不变,动力单元1的传输延时T1为0.6 s;动力单元2的传输延时T2为0.7 s;动力单元3的传输延时T3为0.8 s。
为了验证多变量非线性预测控制方法的有效性,我们模拟高速列车在正常运行情况下,参数突变情况下两种情况下以验证 本文方法可以实现高速列车的高精度跟踪能力,并采用了PID算法与本文方法的仿真结果进行对比。
4.1 正常情况
采用本文控制方法并选取N=3,Nu=2以及PID方法在正常情况下对高速列车在济南至徐州东区间内进行实时跟踪。图5,图6分别是高速列车在正常情况下的仿真速度跟踪曲线,误差曲线。从图5的局部放大图中以及图6误差曲线图中,我们可以看出本文方法实现了对于目标曲线的高精度跟踪,跟踪效果优于PID算法。在对目标速度跟踪过程中没有出现速度突变,均平稳过渡,达到控制效果满足人体的舒适度要求[17]。

图5 正常情况下速度跟踪曲线Fig.5 Velocity tracking curve under normal conditions

图6 正常情况下速度跟踪误差曲线Fig.6 Velocity tracking error curve under normal conditions
4.2 参数突变情况
当动车组机械磨损严重同时存在牵引/制动机构不稳定时,其运行模型的参数就会发生突变,广义预测控制系统有自适应调节能力,以维持元控制性能不变,在面对这样的问题时,我们通过以下仿真实验验证本文方法的有效性。

图7 参数突变下的速度跟踪曲线Fig.7 Velocity tracking curve under parameter mutation

图8 参数突变下的速度误差曲线Fig.8 Velocity error curve under parameter mutation
图7,图8分别为参数突变情况下的速度跟踪曲线,误差曲线。从图7的局部放大图以及图8的误差曲线图中我们可以看出,本文方法依然显示出比PID方法更好的跟踪效果,在参数突变时刻有轻微跃变但后续依然可以保持平稳跟踪,而PID方法有一个较大程度的跳变,且不能保持跟踪效果(后续保持跟踪是参数未突变时的跟踪)。本文方法不会影响高速列车的安全操作以及乘坐舒适感,并在后续跟踪过程中依旧保持了较好的控制性能,没有出现速度的急剧增减,根据上述结果进一步验证了方法的有效性。
5 结论
本文通过分析动车组牵引和制动系统的构成、特性、控制力产出的过程,提出了动车组的多动力单元模型,并利用广义预测控制器结合非线性补偿器实现了对给定目标速度的精确跟踪,在正常实验情况下以及参数突变情况下通过与PID算法进行比较验证了系统的鲁棒性、跟踪性能以及控制效果。仿真结果表明,本文所提方法是可行的满足了较高的要求,实现了高速动车组安全、准时、舒适高效的运行。
