基于ARIMA模型的极端事件下铁路货运量预测研究

孙 斌，陈思伶，杜丽慧

（1.中铁四局集团建筑工程有限公司，安徽 合肥230022；2.华东交通大学经济管理学院，江西 南昌330013）

由于我国的地理条件内陆深、范围广，铁路在我国的物流发展中具有举足轻重的地位[1]。铁路货运量是研究物流需求的重要指标之一，能够为铁路物流基础建设和物流系统的合理规划提供重要依据。铁路工作的规划需要获取未来一定时期的铁路客、货运流量，科学准确的预测铁路流量是铁路规划的前提和基础，能获取不同时间、空间区域的流量特征，为铁路规划提供全面、可靠的参考[2]。然而，在类似新冠疫情这样的极端事件突发时，运输量会呈现出一定的复杂性和不确定性，后续的抗疫工作也会给交通运输业带来较大影响，因此，准确的预测铁路货运量数据与变化趋势对铁路工作的开展有重要的参考意义。

刘月等通过对比考虑滞后期与不考虑滞后期的模型，证明了将滞后性引入吞吐量预测的重要性[3]；DAI在分析影响交通流量因素的基础上，采用多元线性回归方法预测交通流量[4]；黄慧琼采用模糊线性回归算法对交通流量进行预测，但这一方法不适合预测波动大的数据[5]；汪志红等将改进的移动平均自回归模型（ARIMA）应用于月度铁路客运量的预测，分析了季节因素与节假日对铁路客运量的影响[6]；贾学锋利用灰色预测模型进行公路货运量的预测研究，取得了较好的预测效果，实现了小样本数据的货运量预测[7]；原云霄等基于AR I MA模型实现了对公路物流指数的预测过程，并得到了比较好的拟合效果[8]；Kumar等将具有周期性的交通流实时数据处理拟合成参数模型，用季节ARIMA模型对短期交通流进行预测，但拟合程度较差，不适合短时交通流预测[9]；严雪晴，崔乃丹，刘夏，徐莉等用灰色预测模型对货运量、交通流量进行预测[10-13]；江天河，邵梦汝等将神经网络模型应用于客流量及货运量的预测[14-16]；国内外学者对交通运输流量进行了很多研究工作，形成了相对成熟的预测理论体系[17],但对于极端事件影响下铁路货运量的ARIMA模型预测没有得到过验证。

2020年2月，突发的新型冠状病毒肺炎疫情短期内给我国经济社会造成了较大冲击，对各种方式的运输都产生了影响。在疫情防控工作中，交通运输业承受了巨大的压力，直至五月份疫情逐步得到控制，经济逐渐回暖[18]。分析和预测疫情对运输工作的影响能为后续可能出现的风险做好应对准备。选用国家统计局2020年1—2月的铁路货运数据为训练集，2020年3—10月的数据为测试集，寻求适当的ARIMA模型，并做出相关预测。选择这次极端事件发生后2020年3—10月的铁路货运量进行ARIMA模型的预测验证。运用工具为SPSSStatistics 26，将原始数据导入SPSS软件，对数据进行差分、ARIMA建模、Ljung-Box检验等处理，最终输出预测结果。

1 ARIMA模型

ARIMA模型属于时间序列模型中的随机性模型，将不同时间跨度的数据按照时间的先后顺序排列而成，描述了数据样本随时间变化的分布和趋势。美国学者Box和英国学者Jenkins在20世纪70年代提出了ARIMA模型，称为移动平均自回归模型，简记为ARIMA（p，d，q）。其建模思想是将一个随机时间序列用相应的数学模型进行分析研究，深入了解这些动态数据的内在联系及复杂特性，从而进行最佳预测。

AR是自回归，p为自回归项，代表时序数据本身的滞后数；MA为移动平均，q为移动平均项数，代表预测误差的滞后数；d为时间序列成为平稳序列所需要的差分阶数。所谓ARIMA模型，是指将非平稳时间序列转化为平稳时间序列，然后将因变量对它的滞后值以及随机误差项的现值和滞后值进行回归所建立的模型。ARIMA模型根据原序列的平稳情况、回归的内容不同分为移动平均过程（MA）、自回归过程（AR）、自回归移动平均过程（ARMA）以及ARIMA过程。如果时间序列既有趋势变动，又有季节变动，就先要对序列进行n阶差分消除趋势性，再进行季节差分消除序列的季节性，差分步长应与季节周期一致，最终成为平稳序列。

2 ARIMA模型实证过程

2.1 正常数据预测

2.1.1 数据平稳性检验

近年来国民经济快速增长，铁路货运量整体也呈现增长趋势。同时受国家节假日及寒暑假的影响，其变化趋势具有一定的周期性，如图1所示，2010—2019年我国铁路呈线性趋势，并伴随周期为12月的季节波动。利用SPSS软件得到120个货运数据样本的自相关函数（ACF）和偏相关函数，如图2所示，自相关和偏相关图像都是拖尾的，并未衰减到0，因此数据序列是非平稳的。

图1 2010—2019年铁路货运量Fig.1 2010—2019 railway freight volume

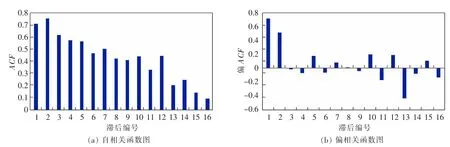
图2 原始数据的自相关、偏相关图Fig.2 Autocorrelation and partial correlation of original data

2.1.2 数据预处理

为消除原始序列的趋势信息，对数据样本做一阶差分。同时为了清除季节信息，对数据做周期为12月的一阶季节差分，序列图如图3所示。分别做完一阶差分和一阶季节差分后作出自相关、偏相关函数图，进一步验证差分运算后的序列平稳性，如图4所示。可以看出此时数据基本平稳。

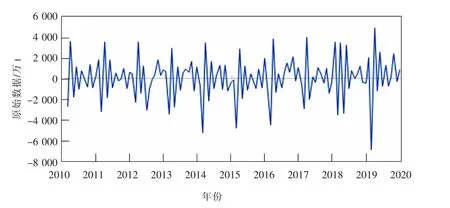
图3 差分后的原始数据序列图Fig.3 Sequence diagram of original data after difference

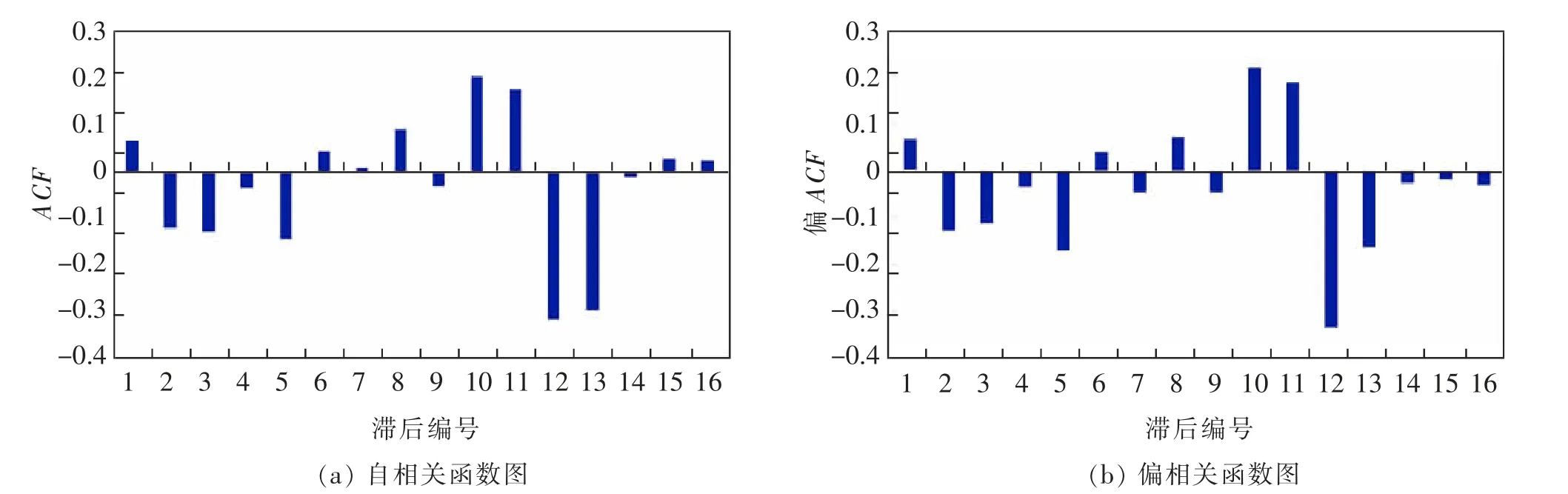
图4 差分后的自相关、偏相关图Fig.4 Autocorrelation and partial correlation after difference

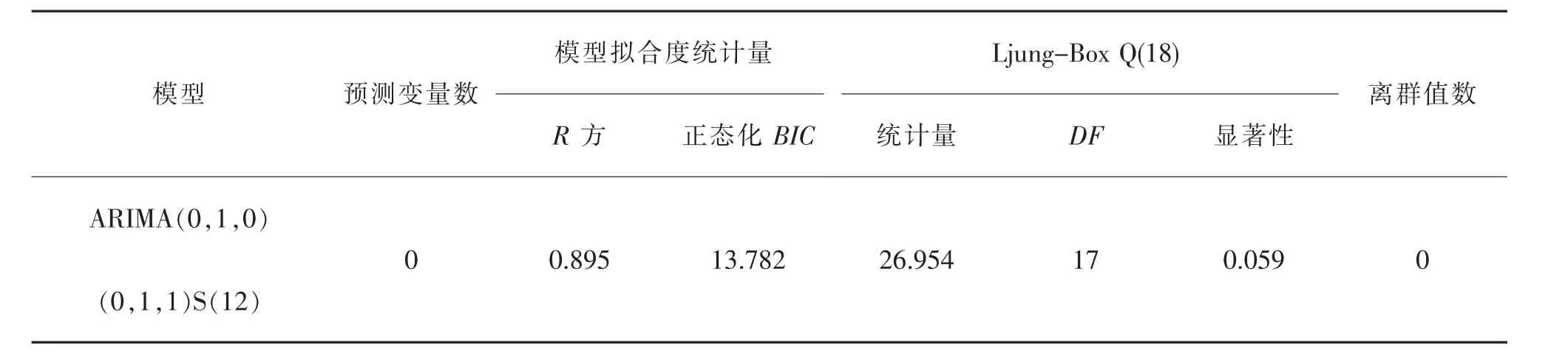
表1 ARIMA季节差分模型拟合度Tab.1 Fitting degree of ARIMA seasonal difference model

通过观察图4选择拟合模型的参数为ARIMA（0，1，0）（0，1，1）S（12）模型。根据所选择的模型进行拟合，结果如表1所示。从表中可以看出，模型平稳的R方为0.895，说明模型能解释原来序列中89.5%的信息，Ljung-Box（杨-博克斯）统计量的值显著，说明ARIMA（0，1，0）（0，1，1）S（12）模型拟合该时间序列数据样本的效果比较理想。

2.1.3 模型预测

建立ARIMA（0，1，0）（0，1，1）S（12）参数模型，应用SPSS软件对2020年1—10月铁路货运量进行预测（表2）。将预测数值与实际数值进行比较可以看出，2020年1—5月疫情期间的预测值与实际值的残差较高，平均残差为4 100.41。其中4月份的残差最高，达4 980.31，5月的残差最低，为2 790。观察数据发现，虽然1—5月的预测残差高，但总体的增减趋势与真实值大致相同，这是ARIMA模型能够捕捉时间序列季节特征的特性。随着疫情的逐步控制，2020年6月起货运量预测值的精度也随之升高，6—10月的平均残差为960.99，预测结果较接近。

表2 2020年正常数据预测值Tab.2 Predicted value of normal data of 2020

2.2 加入异常数据预测

在原始铁路货运量数据基础上加入本次极端事件发生后2020年1—2月的异常数据，再次使用SPSS软件进行ARIMA（0，1，0）（0，1，1）S（12）模型的预测实证，预测值为2020年3—10月，预测结果如图5。可以看到，加入疫情发生后的异常数据预测的3—5月预测残差较低，平均残差为833.75，较正常数据预测结果的平均残差下降79.65%。其中3月的残差绝对值低至125.44，5月的预测残差也较正常数据预测结果下降了1 000.63。6月份起疫情控制，经济回暖，异常数据的预测精度逐渐下降，6—10月的预测残差平均绝对值为3 889.83，是正常数据预测结果的4.05倍。

表3 2020年加入异常数据后预测值Tab.3 Predicted value after adding abnormal data

3 预测结果分析

通过对比正常数据的预测残差和加入异常数据后的预测残差可以发现，正常数据的预测结果在1—5月残差较高，残差平均绝对值为4 100.41，预测精度不理想；待疫情影响逐渐褪去、铁路货运情况恢复正常的6—10月区间，预测精确度较高，残差平均绝对值为960.99，能够准确预测。

加入2月份铁路货运量异常数据进行预测的结果在3—5月精确程度高，残差平均绝对值为833.75，说明该参数模型能够精准预测该区间的货运量；而铁路工作逐步恢复正常的6—10月区间预测残差突升，从5月的1 789.37升高至6月的4 102.23，预测精度下降。

取加入异常数据预测结果的3—5月份，结合正常数据预测结果的6—10月份，可以得到较为精确的2020年3—10月预测值（图5）。从图5可以看出，预测结果较好的验证了ARIMA模型在极端事件发生后异常值与正常值的预测能力。

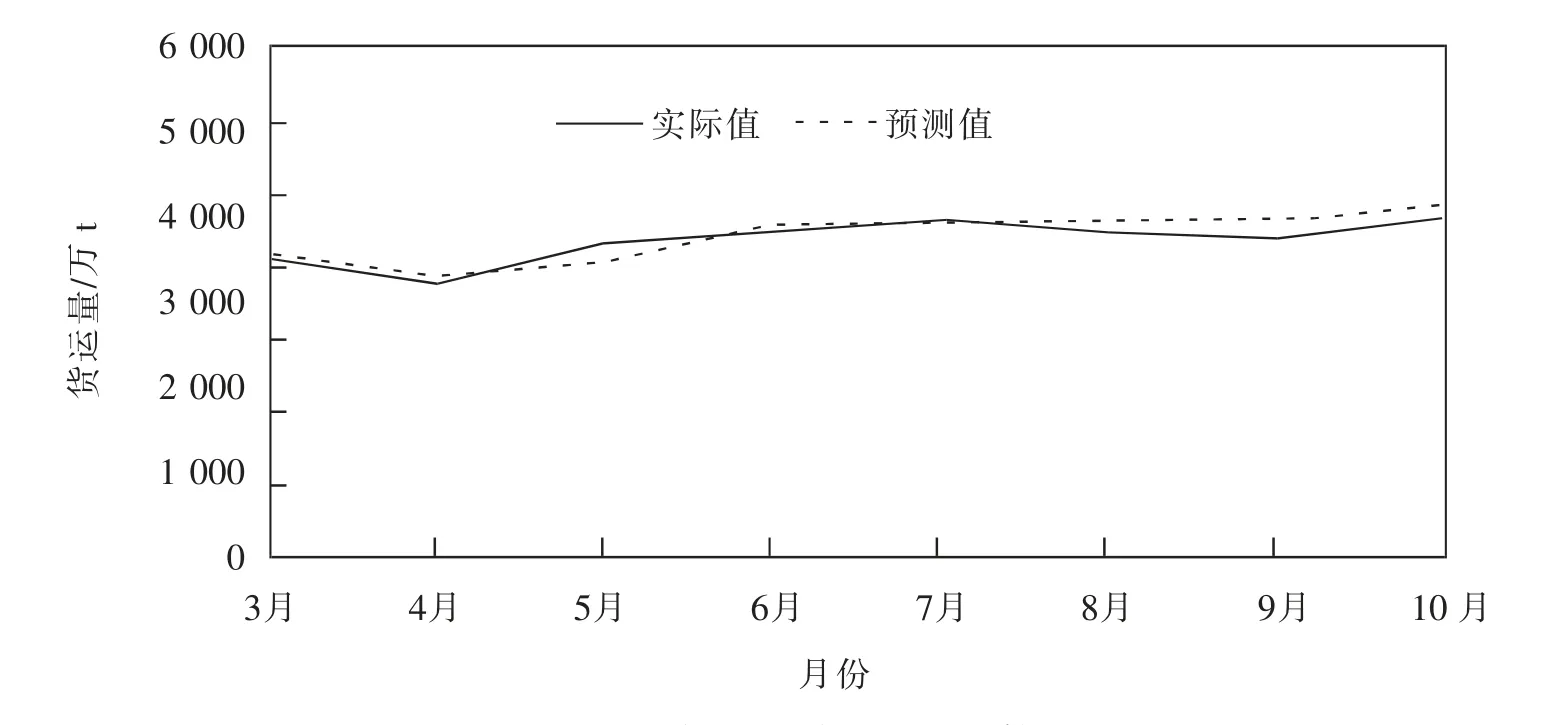
图5 最终预测值与实际值比较Fig.5 Comparison of final predicted value and actual value

4 结论

类似新冠疫情的极端事件会从不同方面影响铁路货运量，准确的进行月度货运量预测对铁路部门的调度工作尤为重要。本文利用2010—2019年的铁路货运量历史数据与疫情发生后2020年2月的异常数据构建ARIMA模型，对2020年3—10月的铁路货运量进行预测。

1）结果表明，原始数据加入极端事件发生当月的异常数据得到的预测值，与事件发生后、影响消退前的真实值较为接近，预测结果精确，验证了ARIMA模型在极端事件影响下的预测能力。而正常数据的预测结果在极端事件的影响逐渐消退后预测精度也逐步恢复，仍然有参考价值。

2）疫情发生后，铁路部门可以利用当月的异常数据结合历史正常数据进行较短的区间预测；待疫情控制、影响逐渐消退，铁路部门可以继续使用正常数据得到的预测结果，这为铁路的运输组织方案及人员配备等提供了重要依据。