基于FE-SEA混合法列车交会对桥梁振动噪声分析

罗文俊，曹 浩，张子正，江学辉，唐康文

（1.华东交通大学土木建筑学院，江西 南昌330013；2.江西外语外贸职业学院，江西 南昌330000；3.中山市东升镇住房和城乡建设局，广东 中山528414）

随着城市轨道交通的快速发展，连续板梁钢-混结合梁已被广泛应用于桥梁结构中，但基于这种结构的声辐射研究还不够完善。桥梁结构辐射噪声属于低频噪声，会对人体机能造成不利影响[1-2]。韩江龙等[3]分析了列车运行时连续梁和多跨简支梁的结构噪声特性，发现邻跨能够影响远场点噪声，连续梁结构无法有效降噪。罗文俊等[4]基于混合法预测了U型梁的振动特性和结构噪声，发现翼缘板的振动在低频区最大，底板的振动在高频区最大。苏庆田等[5]采用单元和荷载增量步技术对钢混结合梁进行有限元模拟。张迅等[6]结合数值仿真与锤击试验，基于箱型梁模型分析了U肋加劲板的振动特性和声辐射性能，结果表明加劲板的振动噪声更为明显，频谱范围较广。高飞[7]采用有限元法计算列车运行过程中桥梁的振动响应，研究表明桥梁的声压级频谱特性与振动频谱分布规律基本相同，峰值频率为160 Hz。张迅等[8]基于现场试验，采用混合法分析了列车运行产生的振动在箱梁各板件中的传播规律和声压贡献量，发现桥梁振动与噪声的主要频段在40～63 Hz。李奇[9]以某地区轨道交通U型梁为研究对象，在列车移动荷载作用下，提出了适用于低频范围内的混凝土桥梁噪声预测方法。张迅等[10]基于平截面假定和声学边界元法分析了桥梁的结构噪声，结果表明振动和噪声的传播具有某种指向性。张鹤等[11]通过建立瞬态噪声有限元-边界元模型，全面评估车桥噪声的声压水平，获得了较理想的精度。

可以看出，上述成果中针对钢-混结合梁的振动和结构噪声研究较少。由于轨道存在着不平顺，列车单双向行驶时施加在桥面上的荷载也存在着变化，非常有必要针对钢-混结合梁结构桥进行振动和结构噪声分析。

1 FE-SEA混合法原理

Langley等[12-13]的研究为FE-SEA混合法理论作出了重要贡献。基于波动理论的混合法，将边界分为随机性边界和确定性边界。

FE-SEA混合法方程可以写成[14-15]

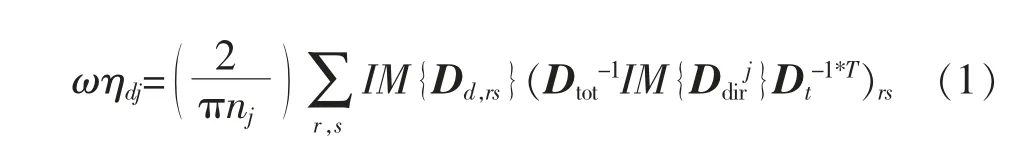
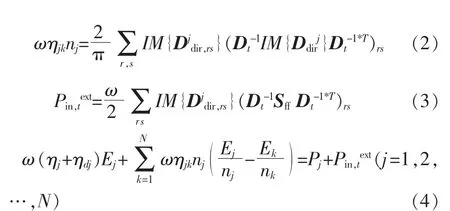
式中：ω为角频率；Ddirj为SEA子系统j的直接场动刚度矩阵；Dt为FE子系统的总动刚度矩阵；ηj为子系统j的阻尼损耗因子；Dd为连接边界处FE子系统自身的动刚度矩阵；ηdj为子系统d和j之间的耦合损耗因子；ηjk为子系统j和k之间的耦合损耗因子；Ej，Ek分别为SEA子系统j和k的统计能量响应；Pj为子系统j的输入功率；Pin，jtext为施加到确定性系统的力而产生的功率；nj为子系统j的模态密度；Sff为施加到确定性系统力的互谱矩阵；r，s为SEA子系统j的确定性边界处的自由度。

将式（1）～式（3）代入式（4），可以求解得到随机性子系统的振动能量。

当单元网格划分较细时，有限元法在低频部分计算精度较高，当模态数较多时，统计能量法适用于高频计算[16]。铁路环境振动影响与噪声的分析主要包括机车车辆、轨道系统和桥梁结构三大子系统，各子系统的振动和噪声影响频率范围不尽相同。采用FE-SEA混合法，结合有限元和统计能量的各自优势，提高了有限元法在高频部分的计算效率，也拓宽了统计能量法在低频部分的应用频率。

2 桥梁结构声辐射原理

将钢-混结合梁视为多个子系统，每个子系统可看作长为b，宽为a的矩形板。对于各子系统，声压辐射功率为

式中：ρa为空间气体的密度；ca为声音在空气中的传播速度；σi为辐射效率；Si为辐射表面积；vi2为均方速度。

3 模型的建立

3.1 列车荷载的模拟

准确模拟列车荷载是研究列车交会对桥梁振动和结构噪声分析的首要前提[17]。选取CRH2动车组，车速为200 km/h。基于多体动力学仿真分析软件SIMPACK，建立车辆-轨道耦合模型，添加轨道高低不平顺谱，计算得到竖向时域轮轨力，经过傅里叶变换得到内1/3倍频程频域轮轨力。

3.2 桥梁计算模型

研究的频率为20～1 600 Hz，桥梁腹板、翼缘、桥面板分别在20，50，200 Hz频率处的模态数大于5。在20～200 Hz频率内，桥面板采用FE子系统，腹板、翼缘采用SEA子系统；在200～1 600 Hz频率内，桥面板、腹板、翼缘均采用SEA子系统。

通过VA one软件建立连续板梁钢-混结合梁双线桥模型。桥面板采用C50混凝土，厚度为0.20～0.48 m。纵梁为2根相距6 m的H型钢梁，高度为2.5 m，宽度1.2 m，腹板的厚度24 mm，翼缘的厚度50 mm。采用板壳类型单元分频段建立模型，在20～200 Hz频率内建立FE－SEA混合模型，在200～1 600 Hz频率内建立SEA模型。

4 振动响应分析和噪声预测

4.1 振动响应分析

在列车单向行驶状态下，提取各板块中心处的振动加速度，转化得到1/3倍频程加速度振级，如图1所示。

由图1可知，列车单向行驶时，各板块的加速度振级变化规律比较相似，峰值频率基本一致，在65 Hz左右；加速度振级的大小规律为：腹板＞下翼缘＞桥面板，该桥梁的主要减振板块为腹板。

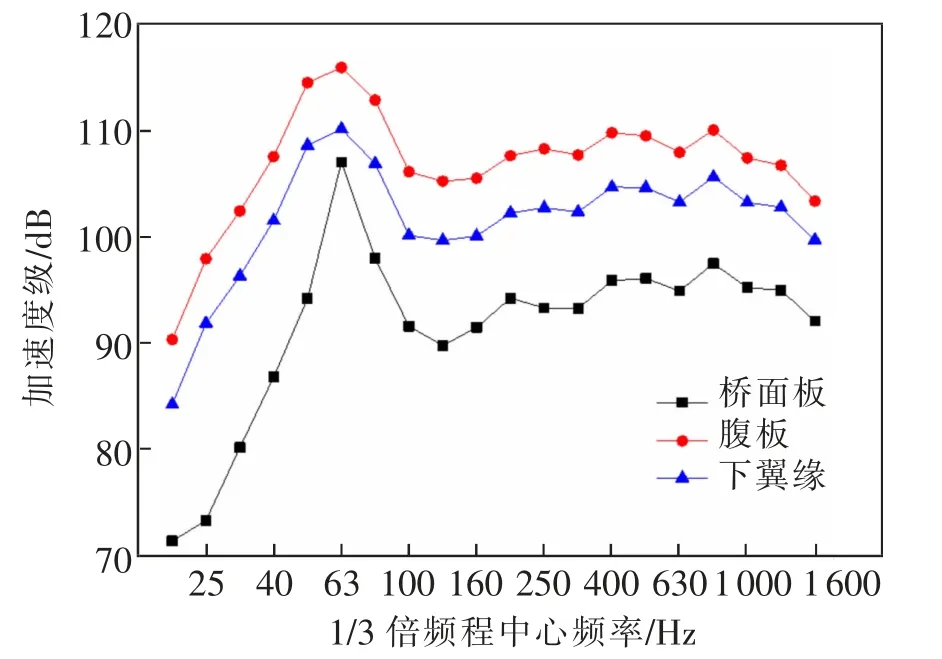
图1 单向行驶各板块中点竖向加速度振级Fig.1 Vertical acceleration level at the midpoint of each plate for unidirectional travel

当桥梁列车交会时，由于车辆荷载和轨道不平顺等因素影响，桥面承受的荷载和激励也随之变化；因此考虑桥梁振动响应和结构噪声的变化很有必要。在2种工况下，各板块中心拾取点1/3倍频程加速度振级频谱曲线对比如图2所示。

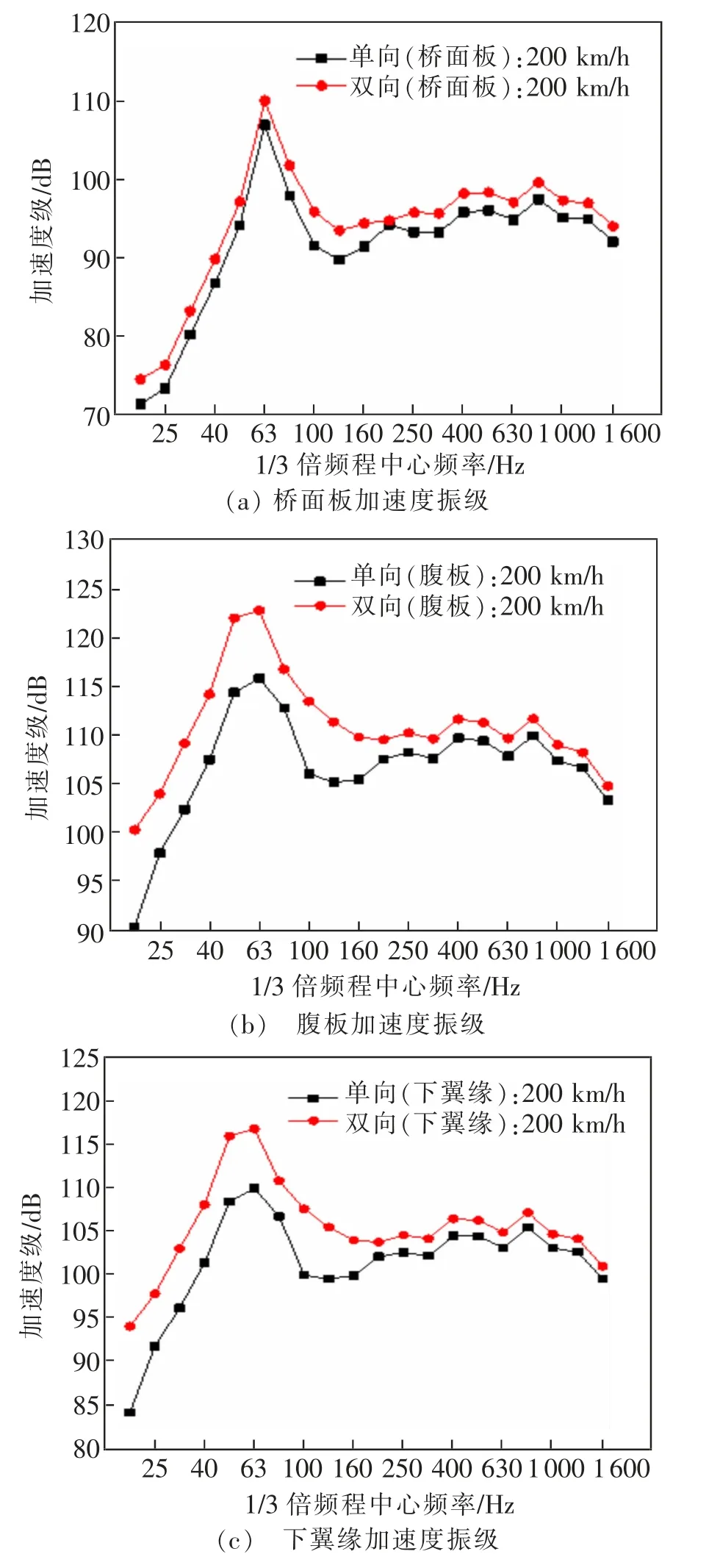
图2 2种工况下各板块中点振动加速度振级Fig.2 Vibration acceleration level at the midpoint of each plate under two conditions

由图2可知，当列车由单向变为双向行驶时，在整个频段内，桥梁各板块中点处的振动加速度振级均有所增大，且变化规律基本一致；优势频段为40～110 Hz，峰值频率为63 Hz，该频率范围可作为主要减振频段。总体而言，腹板的加速度振级最大，桥面板最小，应将腹板作为主要的减振部件。列车交会时对腹板和下翼缘振动加速度振级的影响相比于桥面板较大，主要影响频段为20～200 Hz，对频率在200～1 600 Hz频段的影响逐渐减小。

4.2 结构噪声预测

4.2.1 声场点布置

为分析桥梁辐射噪声对周围环境的影响，在桥梁横断面主跨跨中布置M1，M2，M3和M4共4个噪声场点。M1点布置于轨面上1.2 m，距延轨中心线7.5 m处，M2，M3，M4分别布置在地面上1.5 m，距轨道中心线7.5，25，100 m处。

4.2.2 结构噪声预测

列车单向行驶各场点受到的桥梁结构辐射噪声声压级频谱分布如图3所示。2种工况下各场点声压级频谱分布如图4所示。

由图3可知，当列车单向行驶时，各场点的变化规律相似，M1的声压贡献量最大。近轨中心线至M2范围内的平均噪声衰减频率大于M2至M3范围内。远场点声压级衰减速度较慢，该桥辐射声压级主要频段为60～630 Hz。

由图4可知，在整个频段内，列车交会时桥梁各场点的结构噪声大于单向行驶。2种工况下各场点声压级峰值频率在500 Hz；在列车单向行驶和交会时，M1～M4最大声压级值：M1为78.8，81.3 dB（A）；M2为77.1，79.8 dB（A）；M3为70.1，72.9 dB（A）；M4为58.2，61.2 dB（A）。

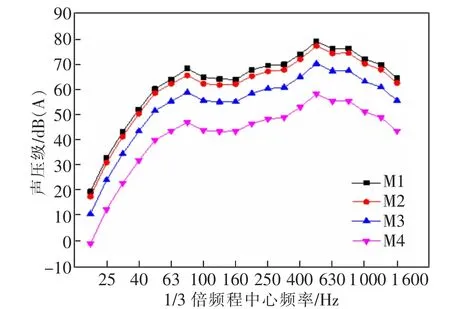
图3 场点声压级频谱图Fig.3 Field points sound pressure level spectrum

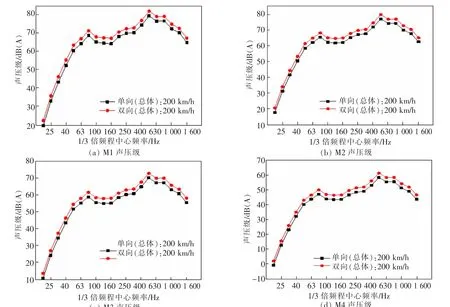
图4 2种工况各场点声压级频谱图Fig.4 Sound pressure level spectrogram of each field point under the two working conditions

4.2.3 声压贡献量

列车单向行驶和交会时场点M1的噪声频谱如图5所示；场点的声压值如表1所示。

由图5可知，列车交会时，全频段内桥面板、腹板和下翼缘结构噪声声压级均有所增大；2种状态下各板块声压级变化规律相似，峰值频率都在500 Hz左右。桥面板的声压级在达到峰值后整体变化幅度较为平缓，幅值为8 dB(A)左右，腹板和下翼缘的声压级呈现相似的变化规律。

综合整个频段，桥梁板块对场点M1～M4的声压值贡献量如表1所示。

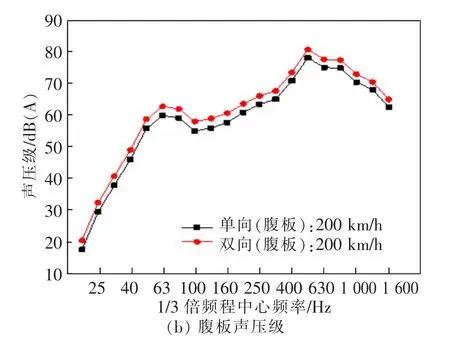
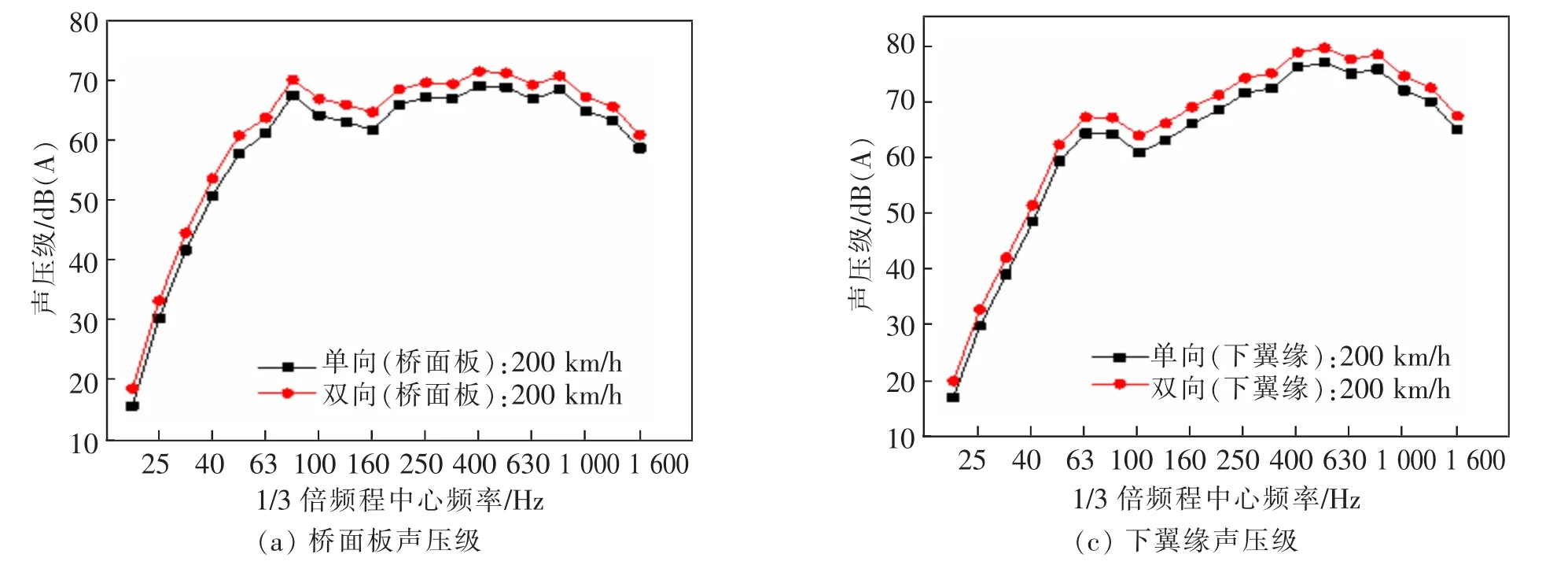
图5 2种工况下场点M1噪声频谱图Fig.5 Noise spectrum of field point M1 under two working conditions

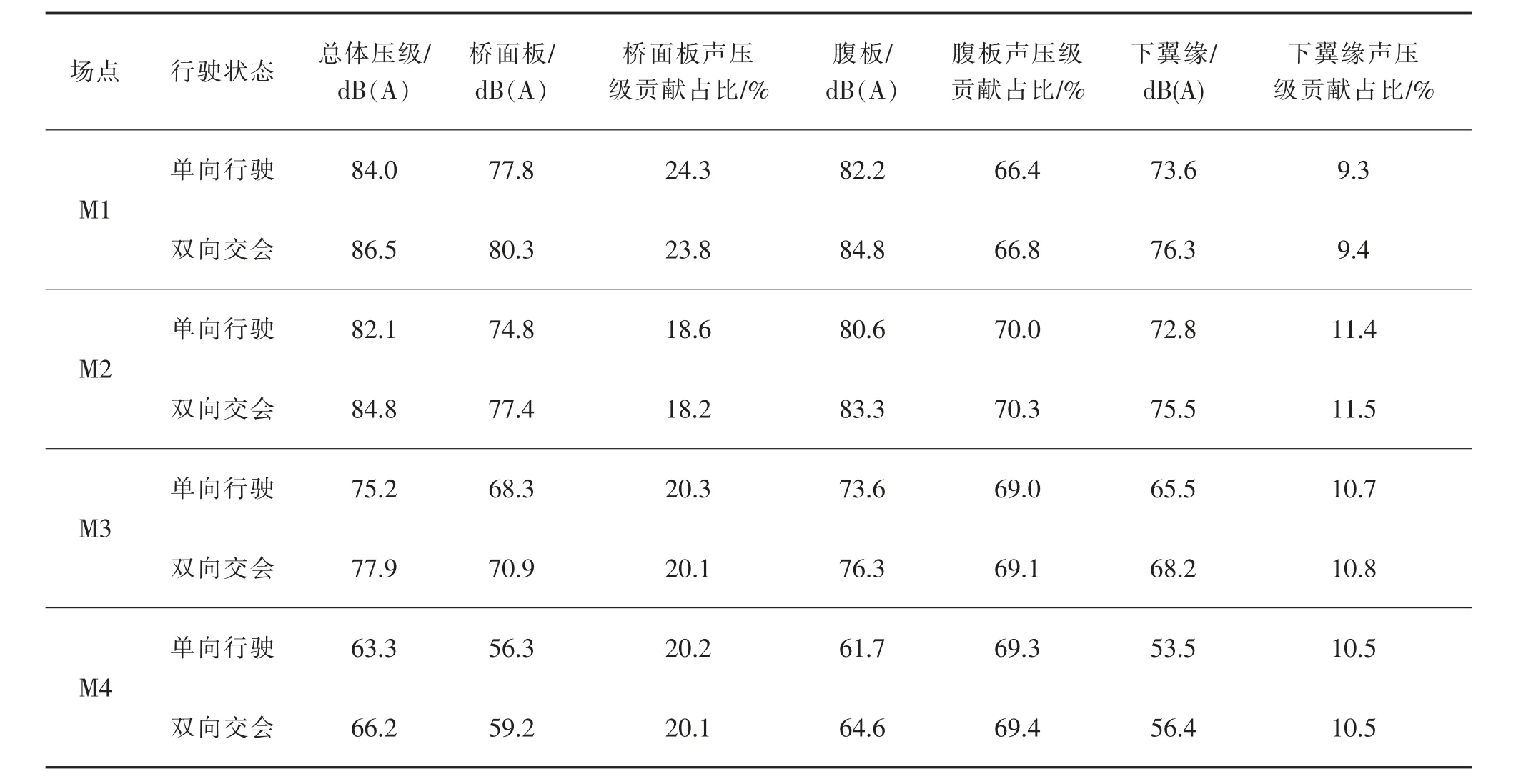
表1 各场点综合频率对应的声压级贡献量Tab.1 Contribution of sound pressure level corresponding to the comprehensive frequency of each field point

在全频段内，腹板对各场点辐射结构噪声的声压级最大，下翼缘最小。各板块对场点声压级贡献量的大小规律为：腹板＞桥面板＞下翼缘；当列车双向行驶时，桥梁的结构噪声逐渐增大，各板块声压级的变化规律为：腹板和下翼缘的声压级贡献量逐渐增大，桥面板声压级贡献量有所减小。

4.3 功率与能量分析

2种工况下桥梁的振动功率级损失如图6所示。

钢-混结合梁的振动功率即为输入功率，由车轨相互作用和梁体产生，结构的振动功率损失为输入功率与输出功率之差。由图6可知，2种工况下的振动功率级损失随着频率的增加均逐渐增大，在40～63 Hz频段有减小的趋势。当列车单向行驶时，桥梁功率损失为13.0～30.0 dB，列车交会时，功率级损失为9.2～27.3 dB。

2种工况下桥梁的振动能量级如图7所示。

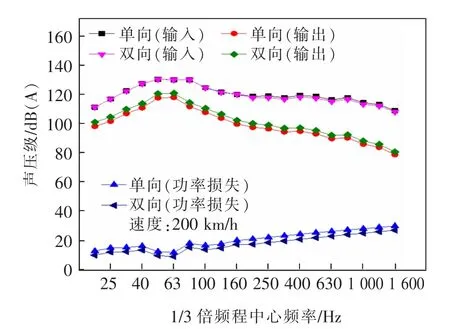
图6 2种工况下振动功率级损失Fig.6 Vibration power level loss under two working conditions

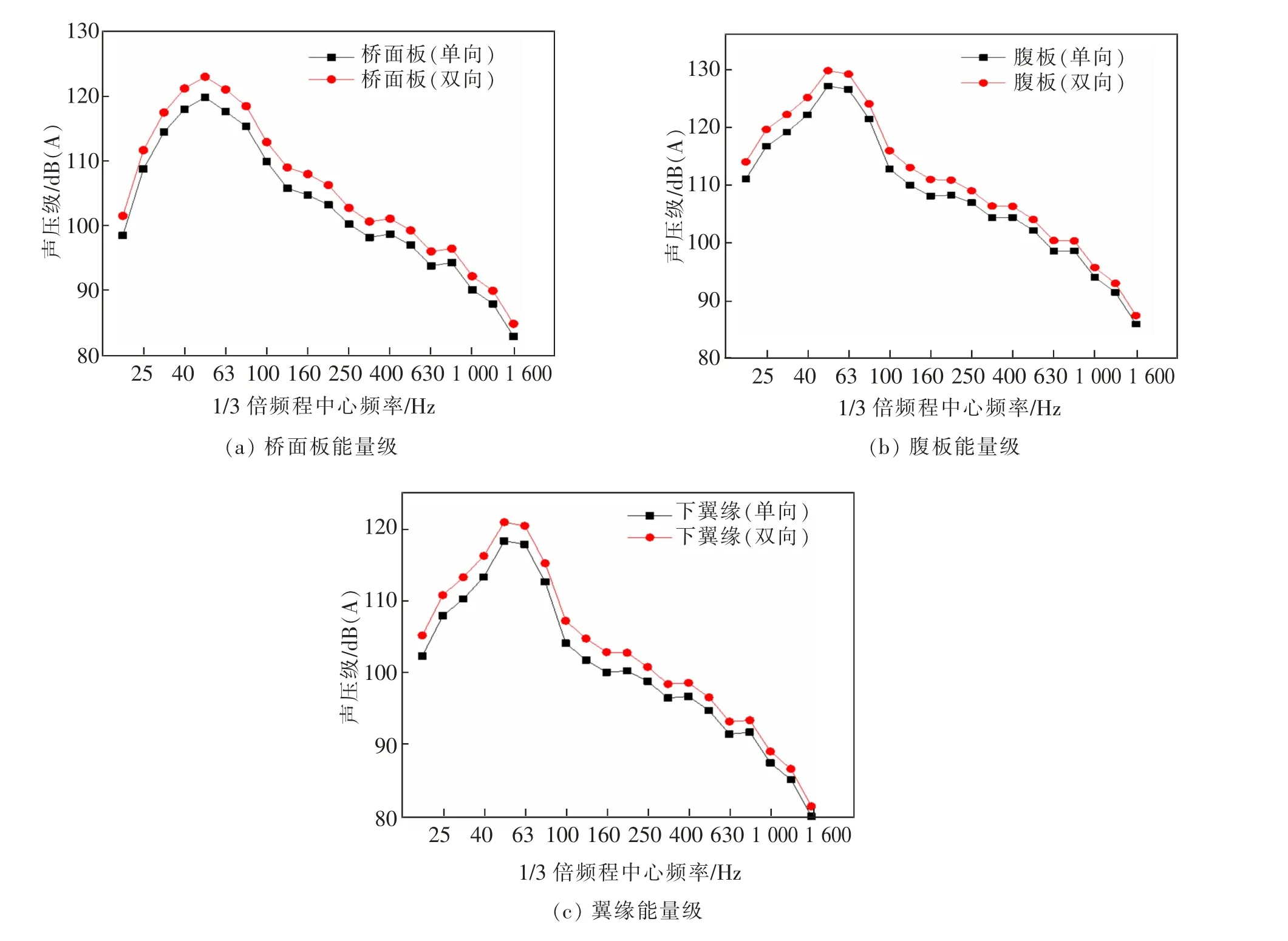
图7 2种不同工况下桥梁各板块的振动能量级Fig.7 Vibration energy levels of each plate of the bridge under two different conditions

由图7可知，列车交会时各板块的能量级在全频段内均大于单向行驶。振动能量级的分布大小规律为：腹板＞桥面板＞翼缘，能量级的峰值频段在50～63 Hz；在低于50 Hz的频段，随着频率的增加各板块的能量级逐渐增大，在50～1 600 Hz频率处，各板块的振动能量级随着频率的增加而减小。在频率为100 Hz时，腹板和下翼缘的振动能量级出现拐点，说明该频率对能量级的影响较大。

5 结论

基于FE-SEA混合法，通过建立钢-混结合梁结构分析模型，对比列车单双向行驶时，桥梁的结构振动和噪声传播规律。

1）桥梁各板块拾取点的振动加速度级均有所增大，且变化规律基本一致，优势频率为40～110 Hz，峰值频率在63 Hz。

2）全频段内各板块结构噪声的声压级均有所增大；2种状态下的各板块声压级峰值频率在500 Hz。桥面板的声压级在达到峰值后变化不大，幅值为8 dB（A）左右，腹板和下翼缘的声压级变化规律较为相似。

3）当列车交会时，桥梁的结构噪声逐渐增大，腹板和下翼缘的声压级贡献量也增大，但增大幅度一般，桥面板的声贡献量减小。

4）当列车单向行驶时，桥梁功率损失为13.0～30.0 dB，列车交会时，功率级损失为9.2～27.3 dB。列车交会时桥梁各板块的能量级在全频段内均大于单向行驶；腹板的振动能量级最大，各板块振动能量级的峰值频率为50～63 Hz。