支持向量机的电力故障检测方法研究
2021-06-17王振国
王振国,贾 飞,余 洋
(内蒙古电力(集团)有限责任公司乌海电业局,内蒙古 乌海 016000)
0 引言
随着电网系统的负荷持续增长以及电网规模的不断增容,影响电网稳定运行的不确定因素也日渐增多。电网故障检测是保障电力系统正常、有效运行的关键技术。相对于传统电网,智能电网可以借助人工智能和机器学习技术,保障电力系统的稳定运行。支持向量机[1](support vector machine,SVM)是一种优秀的机器学习模型。为构造一个最优分类超平面,SVM以最大间隔为优化目标,实现了学习模型的结构风险极小化。它在处理小样本数据方面性能卓越。同时,它的全局最优解可通过优化一个凸二次规划问题来获得。SVM的优势受到了学术界与工业界的关注,并且已被成功地应用了到各大领域[2-4],比如故障检测、场景识别、金融信用、生物识别等。
为解决SVM在处理异构数据分布学习问题上性能较差的不足,Jayadeva等[5]在机器学习领域期刊TPAMI上提出了非平行支持向量机学习范式,并在此基础上给了一个双胞支持向量机(twin support vector machine,TWSVM)模型。相对SVM,TWSVM模型在处理“交叉型”数据问题上表现出卓越的泛化能力,并具有更好的学习效率。因此,TWSVM得到了国内外很多学者的青睐,并后续提出了很多优秀的模型。例如,双胞界限支持向量机(twin band support vector,achine,TBSVM)[6],最小二乘双胞支持向量机(least square twin support vector machine,LSTSVM)[7],双胞参数间隔支持向量机(twin parametric-margin support vector machine,TPMSVM)[8],中心双胞参数间隔支持向量机(centroid parametic-margin support vector machine,CTPSVM)[9],多标签支持向量机(multi-label twin support vector machine,MPSVM)[10-11]等模型。
CTPSVM[9]是近年来被提出的一种非平行机器学习方法,拥有优秀的泛化能力。然而,CTPSVM故障检测模型的解需要通过求解二次规划问题来获得,并不适合处理大规模学习问题。为解决上述问题,受最小二乘法LSTSVM模型[7]启发,将提出一个新的最小二乘中心双胞参数间隔支持向量机(least square centroid twin parametric-margin support vector machine,LSCTPSVM)故障检测模型。该模型旨在使得每个类的样本尽量聚在它所对应的每个超平面的附近,同时其超平面尽量远离样本中心点。对于CTPSVM模型,该模型拥有如下特点:将CTPSVM模型的不等式约束松弛到等式约束,并引入最小二乘法损失函数来惩罚犯错样本;为提高模型的泛化能力,额外的正则项被引入到LSCTPSVM模型中,保障了模型解的唯一性;相对于CTPSVM模型的解需要借助于二次规划的对偶问题来间接的求得,LSCTPSVM模型可直接使用简单而高效的线性方程组系统来获得其原始问题的最优解。在线性和非线性分类问题上,本文提出的LSCTPSVM拥有与CTPSVM相近的泛化能力,但具有更高效的学习效率。
1 中心双胞参数支持向量机
本文采用如下的符号约定:所有的向量都为列向量;上标“T”表示转置;I表示单位矩阵;0和E分别表示全0向量和全1向量。考虑n维实空间Rn中的二分类学习问题[1],给定训练数据集为:
T={(x1,y1),(x2,y2),...,(xt,yt)}
(1)
式中:l为训练集的规模;x∈Rn为第i个训练样本点;yi∈{-1,+1}为训练样本点所对应的类别标签。
此外,记I+和I-分别为属于正类和父类的样本集合索引,其规模分别为l1和l2。
CPTSVM模型[9]的核心思想是,在特征空间中,寻找一对最优的非平行超平面。
(2)
使得每个超平面fk(x)尽量将当前第k类的样本划分为同一侧;另一方面,样本中心尽量在另一侧远该超平面。为实现上述目标,CPTSVM模型[9]优化如下原始问题:
(3)
(4)

类似于SVM,为求解问题和的解,首先将它们转换为对偶问题:
(5)
(6)
然后,当求得对偶问题的最优解α1和α2,可推得原始问题的解:
(7)
(8)
值得注意的是,在CTPSVM模型中,b1和b2的最优解不能直接由对偶解α1和α2计算得到,而是必须通过支持向量与ω1和ω2间接计算得到。对于新样本x的预测,其类别的判别依据如以下决策函数:
Classx=f1(x)+f2(x)=
sign[(ω1+ω2)Tx+(b1+b2)
(9)
2 最小二乘中心双胞参数间隔支持向量机
CTPSVM模型的解需要通过求解二次规划问题来获得,并不适合处理大规模学习问题。为此,受最小二乘法LSTSVM模型[7]启发,提出LSCTPSVM模型,旨在选择一对最优的非平行超平面:
(10)
使得每个类的样本尽量聚在它所对应的每个超平面的附近,同时该超平面尽量的远离样本中心点。为实现上述目标,首先将CTPSVM的原始问题和中的L1模的松弛变量ξ和η转换为L2模,同时将不等式约束。转换为等式约束,构造如下的经验风险函数:
(11)
(12)
式中:c1,c2,μ1,μ2>0为惩罚参数,用于调节损失函数式和中各项损失的权重。

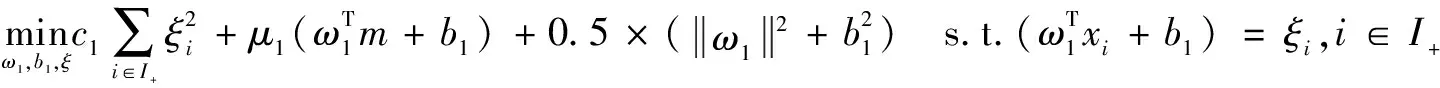
(13)
(14)
接下来,将对LSCTPSVM模型给出解释。首先,讨论和分析优化问题。LSCTPSVM模型的几何解释如图1所示。

图1 LSCTPSVM模型的几何解释
①第1项和约束条件实现了正类样本的经验风险函数。这里使用最小二乘法准则度量正类样本离超平面的距离。对于偏离超平面的正类样本点,引入松弛变量ξi度量其误差。极小化这项期望所有正类样本能聚在正类超平面附近。
②极小化第2项是希望样本的中心点m尽量在超平面f1函数值为负的半空间,且距离超平面f1越远越好。f1(m)越小,则代表正类与负类中的间隔越大,那么模型的泛化能力将会越强。
3 模型优化与求解
将优化问题的等式约束代入到目标函数中,可将问题和转换为如下的无约束的二次规划问题:
(15)
(16)
对于无约束优化问题,其最优解可以通过对J1(ω1,b1)关于变量ω1和b1求偏导:
(17)
(18)
整理可得:
(19)
(20)
同理,对于无约束优化问题,其最优解可以通过J2(ω2,b2)对关于变量ω2和b2求偏导:
(21)
(22)
整理式(21)和式(22),得:
(23)
(24)
优化问题(13)、(14)及其最优解可通过求解式(20)、式(21)和线性方程组获得。相对于CTPSVM通过对偶问题的二次规划间接获得最优解,LSCTPSVM模型可通过求解线性方程组问题来直接优化原始问题获得最优解。对于新样本x的预测,其类别的判别依据如下决策函数:
Cx=f1(x)+f2(x)=sign[(ω1+ω2)Tx+(b1+b2)]
(25)
4 试验结果分析

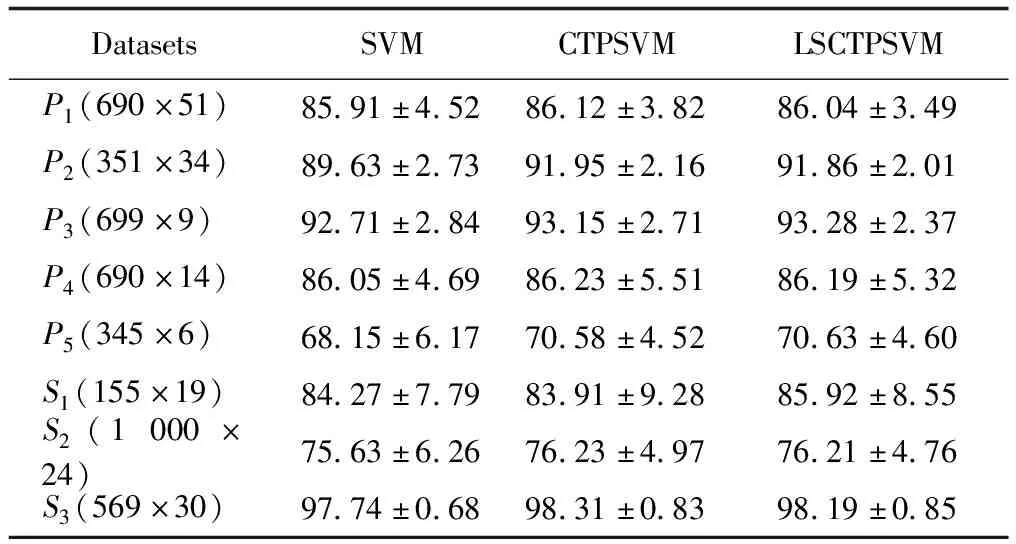
表1 线性各分类器在UCI数据集上的分类准确率对比
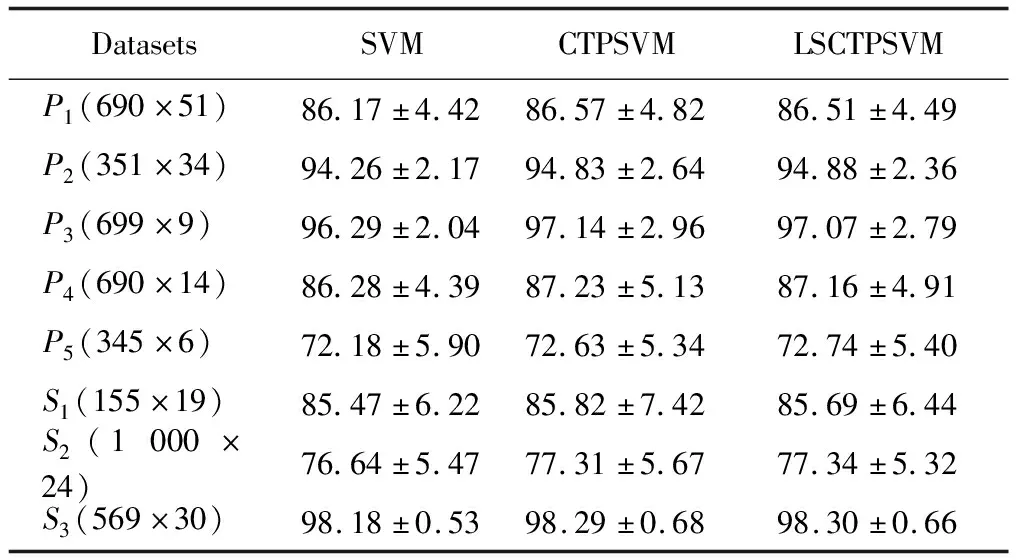
表2 各非线性分类器在UCI数据集上的分类准确率对比
表1和表2分别给出了各模型在UCI数据集上的线性和非线性的平均分类准确率。试验结果表明:本文所提出的LSCTPSVM模型,具有与CTPSVM相近的分类性能。比如对于线性和非线性情况,LSCTPSVM在8个UCI数据集中,分别有3个和4个数据集的分类性能超过CTPSVM。从分类结果的稳定性上看,在大部分数据集,LSCTPSVM的分类方差比CTPSVM的要小,主要原因是在LSCTPSVM模型中引入了额外的正则项b2,可以直接得到模型的最优解,进而提高了模型的稳定性。此外,LSCTPSVM模型在线性和非线性性能在大部分的数据上都超过了SVM。各线性和非线性分类器在UCI数据集上的学习时间比较如图2所示。

图2 各线性和非线性分类器在UCI数据集上的学习时间比较图
试验结果表明:LSCTPSVM模型的训练时间最短,其次是CTPSVM,最慢的是SVM。这是由于LSCTPSVM通过直接优化原始问题,只需要求解一组线性方程组来获得最优解;而SVM和CTPSVM的最优解需要通过求解二次规划问题来获得,时间复杂度较高;同时,SVM优化一个较大的二次规划问题,而CTPSVM和LSCTPSVM将较大的优化问题分为两个较小规模的问题。上述线性和非线性试验结果验证了LSCTPSVM模型的有效性。
5 结论
由于故障检测模型CTPSVM的解需要通过求解二次规划问题来获得,并不适合处理大规模学习问题。为此,受最小二乘法LSSVM模型启发,本文提出了一个新的最小二乘中心双胞参数间隔支持向量机模型,简称LSCTPSVM。该模型旨在使得每个类的样本尽量聚在它所对应的每个超平面的附近,同时该超平面尽量远离样本中心点。本文的主要贡献是:①在LSCTPSVM模型中,首先将CTPSVM模型的不等式约束松弛到等式约束,并引入最小二乘法损失函数来惩罚犯错样本;②为提高模型的泛化能力,额外的正则项被引入到LSCTPSVM模型中,进而保证了模型解的唯一性;③相对于CTPSVM模型的解需要借助于二次规划的对偶问题来间接的求得,LSCTPSVM模型可直接使用简单而高效的线性方程组系统来获得其原始问题的最优解。最后,在公共数据集和电网遥感数据集上,验证了LSCTPSVM故障检测模型的有效性[13]。
