全角模式半球谐振陀螺阻尼误差补偿方法研究
2021-06-17郭锞琛吴宇列张勇猛肖定邦吴学忠
郭锞琛,吴宇列,张勇猛,肖定邦,吴学忠
(国防科技大学智能科学学院,湖南 长沙 410073)
0 引言
半球谐振陀螺(hemispherical resonator gyroscope,HRG)是一种典型的哥氏振动陀螺,具有精度高、寿命长、结构简单等诸多优点。随着近年来国防事业和航天事业的发展,半球谐振陀螺因其在体积、成本等方面的独特优势,受到越来越多的关注[1-3]。
目前,半球谐振陀螺的控制方式大多为力平衡模式(force to rebalanced,FTR)。此模式采用力平衡控制环路产生的反馈力来抵消哥氏力对谐振子振型的影响,根据哥氏力与角速率之间的对应关系,即可由反馈力大小表征出转动速率错误。力平衡模式下的半球谐振陀螺具有极高的精度。但是受制于其控制环路的带宽,其动态范围一般较小,难以满足高动态航天器和武器装备的应用需求。此外,力平衡模式下陀螺输出为角速率值。为得到载体姿态,控制器需要进行积分运算,导致其在长时间工作时会带来较大的累计误差,需要其他导航器的矫正。
全角(whole angle,WA)模式也称为速率积分模式,是区别于传统力平衡模式的一种新型陀螺控制模式。此模式下,谐振子始终处于自由进动状态。通过利用哥氏力引起的谐振子振型进动角度与载体实际转动角成正比这一特性,由解算出的陀螺振型信息直接得到载体转动角度[4-5]。相比于力平衡模式,全角模式无需对谐振子振型进行控制,振型可自由进动,因此具有极大的带宽,可满足高动态武器装备需求。而全角模式直接输出角度信息也避免了积分带来的累计误差,降低了对其他导航器的依赖。
本文对全角模式的工作机理进行了研究,完成了半球谐振陀螺全角模式控制。在此基础上,分析研究全角模式下陀螺输出的阻尼误差,并针对阻尼误差导致的陀螺速率阈值和振型角漂移现象,提出了振型自进动方案和前馈阻尼补偿方案,降低了陀螺的测量阈值和输出波动。
1 全角模式工作机理
1.1 谐振子动力学模型
理想情况下,认为陀螺质量、刚度和阻尼均匀分布,半球谐振陀螺二阶动力学模型如式(1)所示[6]。
(1)
式中:x和y为两个相互正交的信号轴向上的振动信号,在半球谐振陀螺中,x轴和y轴成45°夹角;k为谐振子的进动因子;Ω为载体转动速度;τ为衰减时间;ω为谐振子的固有频率;fx和fy为两个轴上施加的控制作用。
在陀螺处于稳定工作状态时,根据学者Lynch的“均值法”,认为相对于谐振子高频振动,其能量、相位、振型角等参数的变化较为缓慢,从而可将陀螺的“快变量”和“慢变量”分离[7]。将式(1)的通解表示为椭圆参数方程,如式(2)所示。
(2)
式中:a为椭圆的长半轴对应主波波腹;q为椭圆的短半轴对应正交波腹;φ为质点运动的初始相位角;θ为主波腹轴的方位角,与转速Ω存在如式(3)所示关系;θ0为初始方位角。
(3)
对于控制力fx和fy,可将其表示为椭圆长轴方向力和短轴方向力的合成,如式(4)所示。
(4)
Fa和Fq为控制实际陀螺振幅和正交量的力。为维持陀螺的谐振状态,有效力Fa和Fq必须与陀螺的谐振频率保持一致,因此通过频率调制对有效力进行分解。
(5)
综上所述,全角模式下陀螺工作方式为:谐振子通过Fa和Fq维持基本振型。当存在角速度输入,振型会在哥氏力作用下,以kΩ的角速率进动,通过实时检测振型位置,即可解算出载体转过的角度。全角模式工作原理如图1所示。
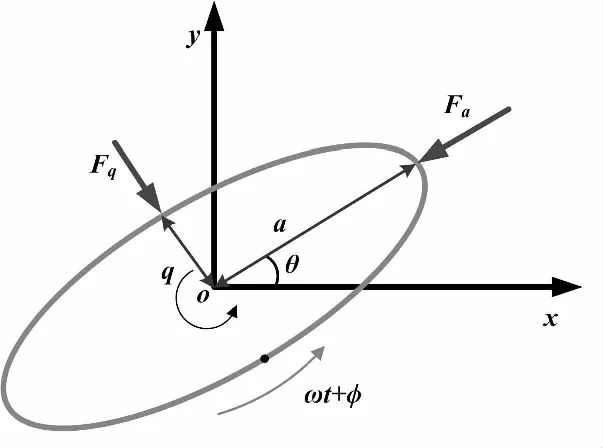
图1 全角模式工作原理示意图
1.2 全角模式测控原理
通过对式(2)中x轴和y轴振动信号的解调滤波,可得到两轴振动的同相分量与正交分量cx、sx、cy、sy,从而计算出全角模式下的陀螺控制量。
(6)
式中:E为振动能量;Q为正交量;θ为驻波的振型角;L用于锁相。
当陀螺存在刚度不均匀和阻尼不均匀时,将导致椭圆参数方程中各参量随谐振子振型角变化,从而造成各控制量中引入刚度和阻尼误差。根据Lynch的理论,其关系可表示为:

(7)
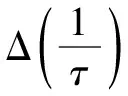
根据式(6)即可得到全角模式控制的四个环路[8-9]:能量控制环路,正交量控制环路,角度输出环路以及锁相环路。全角模式半球谐振陀螺控制电路框架如图2所示。对应的控制目标为:能量保持恒定,正交量控制为0,角度自由进动,驱动频率锁在谐振频率。

图2 全角模式半球谐振陀螺控制电路框架图
2 全角模式输出误差分析与补偿方法研究
2.1 误差机理分析
对式(6)中的角度输出环路进行分析可知,振型角变化由以下几项导致:外界角速度输入,阻尼和刚度不均匀引起的漂移,系统的控制力fqs。
当陀螺在全角模式下正常工作时,系统施加的控制力fqs为0;频率裂解通过对谐振子的静电修调降低为较小值[10];正交量通过正交控制环路的控制抑制为0。此时,角度输出可简化为:

(8)
因此,阻尼不均匀引起的漂移为全角模式下的主要误差来源。
2.2 阈值效应与振型自进动技术
当外界角速度输入较小时,由于陀螺阻尼不均匀地存在,实际的输入信号将会淹没在陀螺自身的漂移中,使全角模式存在速率阈值的缺陷。这也导致了在低角速率输入时,陀螺输出的相对误差大幅提高,影响陀螺标度因数线性度。
为突破速率阈值的约束,可采用自进动的方式使陀螺的振型以恒定的速率进动[11],即通过控制器设置fqs为一常值驱使振型进动。则系统实际求解出的角速率为外界输入角速率与自进动角速率的叠加,如式(9)所示。

(9)
当自进动速率远大于实际陀螺输入时,振型自进动能够大幅提高全角模式下的有效输出;在降低陀螺速率阈值的同时,也能减小阻尼漂移在陀螺输出中的占比。
2.3 前馈阻尼补偿
阻尼补偿原理如图3所示。

图3 阻尼补偿原理框图
阻尼不同于刚度,在陀螺加工完成后难以通过修调等外界控制简单地改变。为减小阻尼漂移影响,考虑施加随振型角变化的补偿力u,以抵消式(9)中角度的阻尼漂移项。

(10)
式中:u的各项参数需通过前期对谐振子阻尼分布的测试得到。
3 试验测试与分析
3.1 振型自进动降低陀螺阈值效果测试
为测试全角模式下半球谐振陀螺速率阈值,将陀螺固定在试验转台上,控制转台以较低的角速率转动,并逐步减小转台转速,观察陀螺输出变化。当转台转速降低至0.01 °/s时,根据陀螺输出拟合出角速率约为0.004 4 °/s,已经降至实际输入的50%以下,如图4所示。
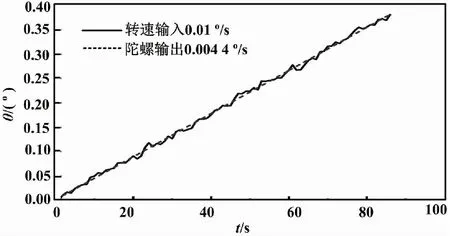
图4 全角模式下半球谐振陀螺阈值测试结果
当采用自进动方案控制陀螺振型时,采用同样的测试方法。当转台转速降至0.005 °/s时,在正转和反转两种情况下,陀螺测得的有效角速度分别0.004 7 °/s和0.005 2 °/s,仍然未达到速率阈值,如图5所示。这表明自进动能够有效降低全角模式下测量的速率阈值。

图5 振型自进动条件下阈值测试结果
此外,根据图5中自进动下陀螺的输出情况,可以明显观察到陀螺阻尼不均匀导致输出的正弦波动,进一步证实了阻尼误差对陀螺输出的影响。
3.2 阻尼补偿效果测试
补偿前后陀螺角度输出波动对比如图6所示。在无外界角速度输入情况下,控制陀螺振型以恒定速率自进动。在扣除自进动角度后,得到陀螺实际输出如图6中实线所示。该曲线表征出陀螺周向阻尼分布对陀螺输出的影响,与前文分析的结果相符。在此基础上设置补偿力对陀螺进行补偿,得到补偿后测试结果如图6中虚线所示。其波动峰峰值由补偿前的0.37°降低至了0.048°,有明显提升。
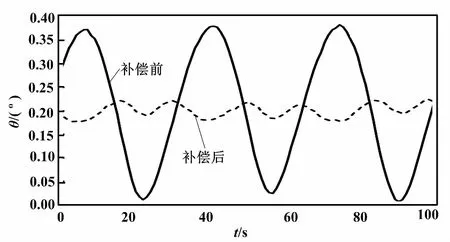
图6 补偿前后陀螺角度输出波动对比图
4 结论
本文对全角模式半球谐振陀螺的工作原理进行了研究,介绍了半球谐振陀螺在全角模式下的运动模型和控制方案,并且针对阻尼误差导致的速率阈值和振型角漂移提出了对应的解决方案、进行了试验验证。试验采用振型自进动的方法,突破了试验采用的半球谐振陀螺原本0.01 °/s的速率阈值限制。在此基础上施加了阻尼前馈补偿,使阻尼不均匀导致的陀螺输出波动由之前的0.37°降低到了0.048°。试验中采用的补偿方案不仅针对半球谐振陀螺,对杯型陀螺、环型陀螺等哥氏振动陀螺也能够起到补偿作用,对阻尼不均匀性的补偿有一定的参考价值。
