深度学习网络的微电网变压器电压波动抑制研究
2021-06-17郭永鑫肖洪光
郭永鑫,肖洪光,杨 璐
(国网吉林省电力有限公司,吉林 长春 130062)
0 引言
微电网作为充分发挥分布式能源效用的主要形式,能够满足当前能源需求的快速提升。其中,以变压器为核心的微电网结构成为当前研究领域的关注热点[1]。微电网变压器受干扰后易产生电压波动问题,严重影响微电网供电质量,直接或间接导致的经济损失越来越严重[2]。抑制变压器电压波动需以准确的电压波动估计为基础[3]。
作为机器学习的主要组成结构,深度学习网络通过学习样本内在规律完成信息识别[4]。深度学习网络中的置信网络具有特征提取与分类功能[5],可应用于变压器电压波动估计。为此,提出了基于深度学习网络的微电网变压器电压波动估计与抑制方法,采用深度学习网络完成特征提取功能,以自动生成特征替代人工设置特征,准确估计电压波动情况;在电压出现波动条件下,通过组合抑制方法抑制其波动,保障微电网的稳定运行。
1 微电网变压器电压波动抑制方法
1.1 微电网系统结构
微电网系统结构包括主电网、变压器、光伏阵列、风机、蓄能系统等[6]。变压器包含三个层级[7],分别是H桥型交流电源(alternating current,AC)与直流电源(direct current,DC)变流器级联构建的输入级、双向全桥DC-DC变换器变流器并联构建的隔离级、完成电压源型逆变的输出级。三个层级分别具有连接主电网不同电压等级、变换电压、提供低压交流接口引出微电网交流母线的功能。微电网交流母线利用DC-AC、AC-DC-AC变换器连接风机与光伏等分布式能源。具有辅助本地供电功能的蓄能系统利用DC-AC变换器与微电网连接。微电网系统结构框架如图1所示。

图1 微电网系统结构框架
变压器受干扰后易产生电压波动问题。引起微电网变压器电压波动的主要因素如表1所示。基于微电网变压器电压波动主要因素造成的电压波动波形,采用深度学习网络中的置信网络构建模型,提取波形特征,根据特征估计电压电压波动情况。

表1 微电网变压器电压波动的主要因素
1.2 变压器电压波动估计
1.2.1 深度学习网络结构
作为具有多隐含层的神经网络,深度学习网络中反向传播(back propagation,BP)神经网络和受限玻尔兹曼机(restricted boltzmann machine,RBM)的数量分别为一层和多层。通过逐层贪婪学习算法调整不同层级之间的连接权重。无监督学习性能极强,能够最大限度地防止类别划分性能较差以及过度拟合缺陷的出现[8]。图2所示为深度学习网络结构。
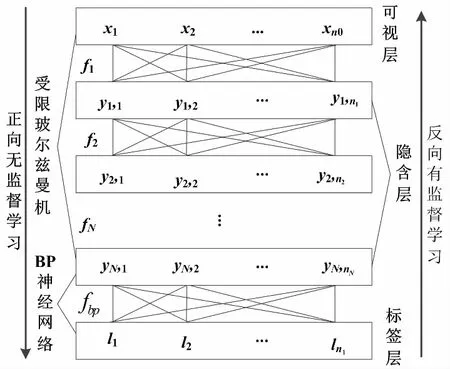
图2 深度学习网络结构图
图2中:x1、x2、xn0、f1、f2、fN和l1、l2、lnl分别为可见层输入情况、相邻单元层间连接权重向量和标签层不同单元情况;yx,z和ftp分别为第x个隐含层第z个单元情况和BP神经网络权重向量。
作为基于能量函数的概率建模方法,受限玻尔兹曼机由可视层和隐含层共同组成[9]。其主要功能为利用栈式逐层堆叠学习初始数据内复杂化准则。深度学习网络训练由三个环节组成,分别是模型初始化环节、正向无监督学习环节和反向有监督学习环节。
1.2.2 深度学习网络计算原理
设(v,y)为给定状态,通过式(1)能够描述深度学习网络可见层和隐含层单元的统一设定能量函数:
(1)
式中:λ=(f,ε,φ)为深度学习网络参数;fij为第i个可见层单元与第j个隐含层单元之间的权重,只有邻近两个层间具有连权重接;εi为第i个可见层单元;φj为第j个隐含层单元的偏置;vi、yi均为状态参数;n为可见层单元数量;m为隐含层单元数量。
深度学习网络状态概率具有正则分布特性[10],因此可利用式(2)描述随机状态的统一概率分布:
(2)


(3)
(4)
式中:s为训练样数量。
利用深度学习网络对数似然函数L(λ)最大化处理,获取深度学习网络参数λ,同时拟合训练样本。此时,可视层输入数据的特征为隐藏层:
(5)
将比散度算法应用于对数似然函数中[11],求解λ。以λ内包含的fij为例:
(6)
式中:Dvi,yj,1为训练样本参数;Dvi,yj,2为深度学习网络定义的期望参数。两者均可通过吉布斯采样获取。
在此基础上,可优化fij,得到:
fij=βfij+α(Dvi,yj,1-Dvi,yj,2)
(7)
式中:β为动量参数;α为学习率参数。
εi与φj同样可采用上述过程实施优化。
1.2.3 基于深度学习网络的电压波动估计
深度学习网络中,不同隐含层特征向量维度与其单元数量相同。隐含层数量越多,模型提取的特征精度越高,电压波动情况估计越准确。
电压波动估计的实现流程是通过采集微电网变压器电压波动波形时域数据,经过数据预处理后建立批量输入深度置信网络模型。结合RBM正向无监督学习数据各层的特征,采用逐层贪婪算法修正各层单元的偏置值和隐层权重,并对顺序输入的不同电压波动波形进行准确分类和标志。利用BP神经网络对训练样本进行反向微调,完成模型训练。根据输入电网的数据,可以准确地提取出微电网变压器的电压波动特征。
1.3 电压波动抑制
采用深度学习网络提取电压波动波形特征完成电压波动估计。若电压出现波动,则需对其进行抑制,保障微电网稳定运行。在采用比例谐振控制器作为抑制变压器电压波动的基础上[12],考虑到变压器的可用补偿容量,可得比例谐振控制器控制下变压器输出电压为:

(8)
式中:EU(γ)为电压控制器传递函数;EI(γ)为电流内环比例增益函数;K为调制增益参数;U2为输出级参考电压参数;i1为输出电流参数。
根据式(8)可知,利用电压控制器抑制电压波动过程中,输出电流i1正向增益EIR(γ)的变化将导致变压器等效阻抗发生变化。
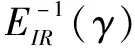
(9)
U1(γ)=EU(γ)U2-x(γ)i2-(1-O)x(γ)i2
(10)
式中:O为补偿系数参数;i2为谐波分量参数;输出层基波等效输出阻抗参数。
O值能够实时抑制变压器电压波动,其取值范围在0~1之间。其值为0和1时,分别为变压器当前为未补偿和全补偿状态。O值与谐波阻抗呈反比关系。O值的提升可使电压器电压波动得到抑制,其值可根据变压器可补偿容量和实际谐波输出容量得到。
2 实例验证
以某微电网为研究对象,在监测系统中采集1 000组电压数据。以800组实测变压器电压波动数据作为训练样本,微电网功率缺额和变压器投切数据分别为180组和170组,短路故障数据为450组(单相接地、两相短路和三项短路分别为150组)。剩余200组作为测试样本,不同类别数据数量一致。
2.1 微电网变压器电压波动估计测试
采用本文方法进行研究对象变压器电压波动估计,构建深度学习网络。模型输入层单元数量同变压器电压波动监测节点数量一致。隐含层共6层,各层内均包含8个单元,第六层隐含层单元数量与提取特征数量一致。输出层单元数量同电压波动数据类型一致。由此确定,试验过程中本文方法所用深度学习网络共包含8层,总节点数量为1个输入层×180+6个隐含层×8+1个输出层×5=233个。设定模型参数:受限玻尔兹曼机迭代次数上限、学习率、动量参数分别为60、0.2和1。在深度学习网络内输入预处理后的训练样本数据。由于模型第六层隐含层单元数量为8,因此模型提取特征数量为8个。特征提取结果如表2所示。由表2可知,相同类型特征数据一致度高,而不同类型间特征数据差异显著。这说明本文方法能够有效提取电压波形特征,且特征显性突出,有利于提升电压波动估计精度。

表2 特征提取结果
根据提取的特征对测试样本进行估计,结果如表3所示。由表3可知,本文方法估计精度达到98.5%,充分说明本文方法能够准确进行电压波动估计。

表3 测试样本估计结果
2.2 微电网变压器电压波动抑制测试
在估计正确的测试样本中随机选取一组样本,采用本文方法进行波动抑制。设定补偿系数值为0.8,压波动抑制结果如图3所示。
分析图3(a)可知,初始电压波形中由于电压波动导致波形畸变显著,电压波形整体畸变率达到18.8%。
分析图3(b)可知,采用本文方法抑制电压波动后,电压波形与初始电压波形相比更为平滑整体,波形畸变率降至2.9%,下降幅度为15.9%。由此说明本文方法能够显著抑制电压波动,保障微电网稳定运行。

图3 电压波动抑制结果
2.3 补偿系数设定分析
本文方法在不同补偿系数设定值条件下,初始电压波形畸变率下降幅度和电压波动抑制过程中的能耗,补偿系数设定如表4所示。由表4可知,随着补偿系数由0.2上升至0.9,畸变率下降幅度和能耗均随之表现出明显的上升趋势。当补偿系数为0.8时,畸变率下降幅度达到15.9%,能耗为4.76 J;当补偿系数升至0.9时,畸变率下降幅度虽然上升0.7%,但能耗却提升2.68 J,畸变率下降幅度与能耗提升不匹配。因此,补偿系数确定为0.8。
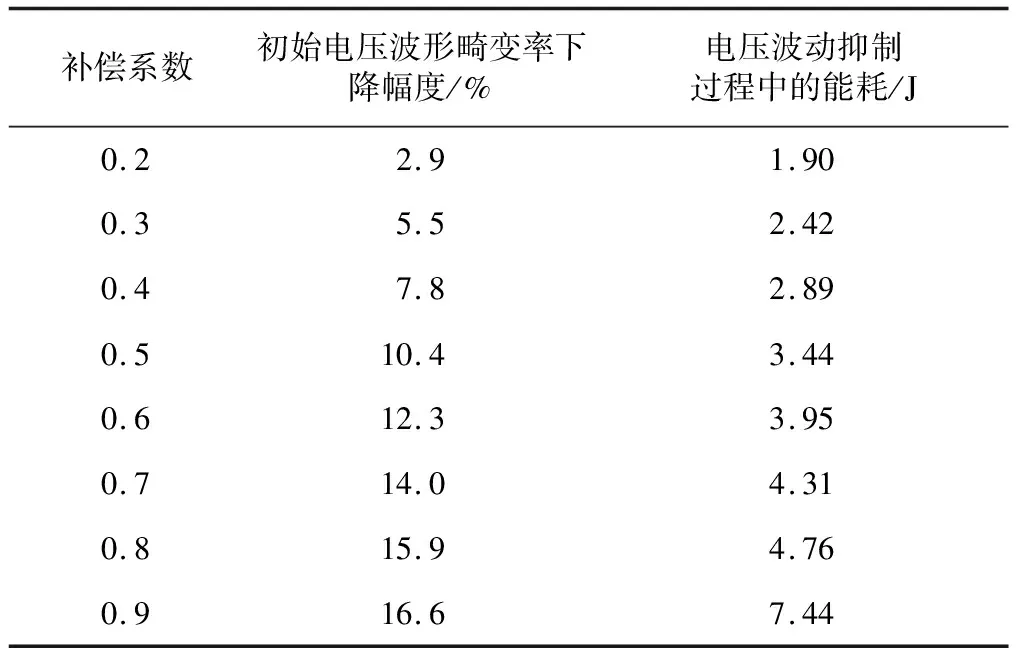
表4 补偿系数设定
3 结论
本文研究深度学习网络的微电网变压器电压波动估计与抑制方法,利用深度学习网络中的置信网络提取电压波动特征估计电压波动情况,并提出一种组合抑制方法抑制电压波动。试验结果显示,本文方法能够准确估计电压波动情况,并显著改善电压波形畸变率,具有较高应用价值。
