几种重要晶须生长基元稳定能计算的数学方法

吴健松，简 艺

(1.广东茂名幼儿师范专科学校，广东 茂名 525000；2.岭南师范学院化学化工学院，广东 湛江 524048)

1 前言

2 基元稳定能计算式

稳定能计算式如下：

(1)

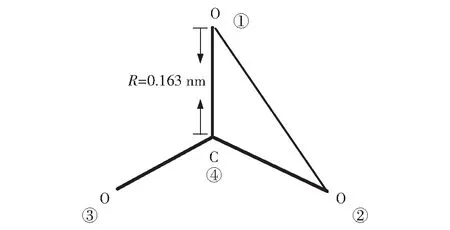
式中：U——稳定能，J/mol；N——常数6.02×1023；e——电量1.6×10-19；ε——当前体系的介电常数；R——阴阳离子之间的距离；n——波恩指数;m——基元所含的离子数;Zi、Zj——分别是同一基元中相邻两个离子所带的电荷;aij=Rij/R,其中Rij表示同一基元中相邻两个离子之间的距离。

从公式(1)可见，影响稳定能大小的参数大多数是基元本身，例如Z、R等。外界因素仅有介电常数，介电常数因晶须体系组成的不同而可能会有数量级的变动，这的确也会对基元稳定能产生数量级的变动。对于同一晶须生长体系的任一种生长基元来说，其介电常数都是一样的，都会有同幅度的变动。因此，基元本身固有的物理量仍然是比较稳定能大小非常重要的指标。

2.1 碳酸根构型为平面正三角型)

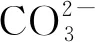
图平面正三角形结构

体系介电常数ε在此处的值为2.54×10-8，波恩指数n=7，基元离子数m=4,阴阳离子半径R=163 pm。由(1)式，得：

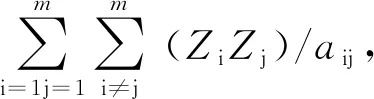
则U=31.714×30.928=9.808×102J/mol

营改增政策的实行凸显了一批企业财务人员水平不高的问题。由此，提升企业财务人员专业素质刻不容缓。企业应为企业内财务人员进行业务培训提供便利，让其经常性参加由专业人士举办的财务知识讲座学习等，通过讲座学习使财务人员掌握良好的企业财务管理方法，更新财务管理知识系统，切实提高财务管理水平。

凡呈正三角形结构的生长基元都可通过上述方法予以计算。

2.2 六氟合铝([AlF6]3-，构型为正八面体)

[AlF6]3-是正八面体结构，如图2所示。

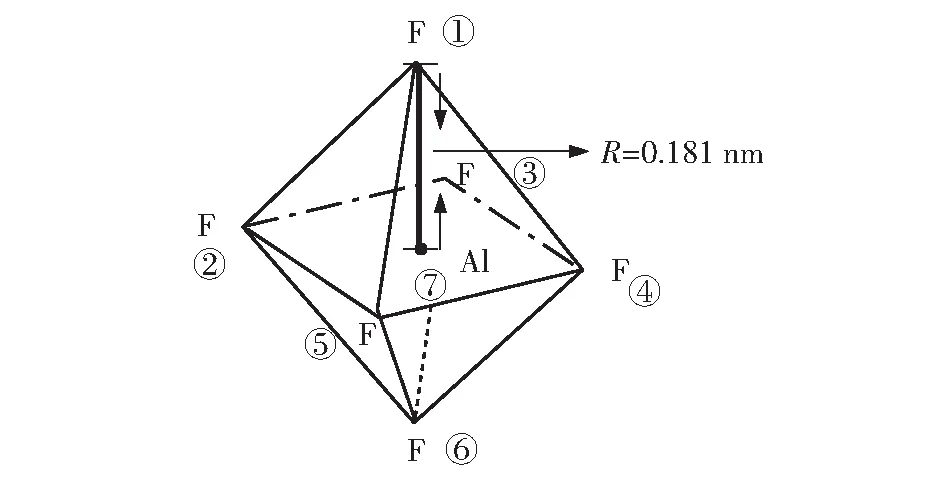
图2 [AlF6]3-正八面体结构

此体系介电常数ε为1.06×10-9，n=7，m=7，R=181 pm，依(1)式，计算过程如下：

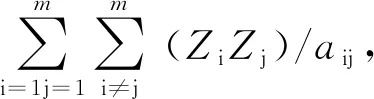
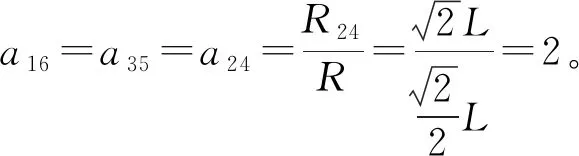
Z1=Z2=Z3=Z4=Z5=Z6=1,Z7=3,

则U=3.195×102×27.958=8.932×103J/mol

2.3 硫酸根构型为不规则四面体)

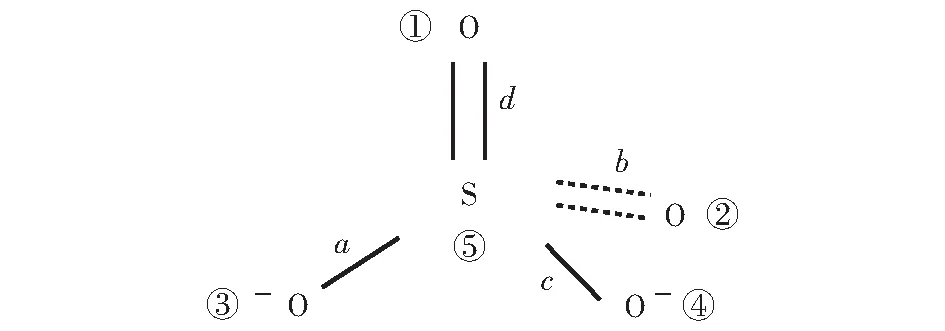
图四面体结构

圆圈中的数字是将离子作标记，以便计算。其中,键长a=155 pm，b=142 pm，c=152 pm，d=143 pm；键角∠ad=116°，∠ab=104°，∠ac=112°，∠bd=98°，∠dc=117°，∠bc=109°；介电常数ε在此处的值为5.12×10-8；波恩指数n=8；基元离子数m=5；关于R的取值，在此较复杂，因为a≠b≠c≠d，经(结合正负离子相互作用及基元拉曼光谱的)研究，R是应取a、b、c、d的调和平均值而不是算术平均值或几何平均(这一条规则不仅适用于四面体结构，同时也适用于其他构型如三角形、八面体形等的结构，即凡是遇到阴阳离子半径互不相等的，都应取调和平均)。

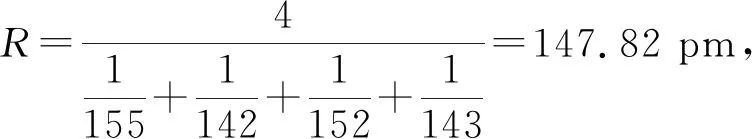
则硫酸根的稳定能为：U=Uc=14.187×62.785=8.907×102J/mol

3 结论

根据晶须生长基元的空间结构，准确画出其几何图形，然后将几何图形与稳定能计算式各参数有机结合起来，逐个对照，逐个计算，保证计算数据的准确性是精准计算基元稳定能各个参数的前提。对于求和项，需先读懂连续求和符号的表达的数学意义，一项项仔细分析，细心求解，展开求和项计算时不能有误漏，否则将造成很大的误差。需注意，如果遇到阴阳离子半径不相等时，应取调和平均而不是算术平均或几何平均。只要深刻理解稳定能计算式各参数的物理意义，同时充分理解基元几何图形中点与线分别代表什么原子和化学键，理顺好基元几何图形与生长基元中各离子之间的空间关系，认真细致地对待每一计算步骤，再复杂繁锁的稳定能计算都能精准算出，再复杂的问题都可迎刃如解。介电常数虽然对稳定能影响较大，但是，在同一生长体系中，对于任一基元介电常数都是一样的，所以在进行对比时可约去介电常数。因此，各个基元自身稳定能仍然是十分重要的。