基于非线性拟合的电池剩余容量预测

吴杰，陈辉

（安徽商贸职业技术学院基础教学部，安徽 芜湖 241002）

1 问题的提出

近年来，国内外针对电池放电问题进行了大量研究。丁丽等利用曲线、曲面拟合给出了电池放电模型，但未对初始放电状态进行研究，且拟合结果不够精确[1-4]。付春流等提出基于支持向量回归的剩余放电时间预测方法，但是需要对数据单独研究，而且预测比较繁琐[5]。侯国亮等提出基于指数函数的函数拟合方法，但计算出来的平均相对误差（MRE）较高，而且预测精度较低[6-8]。覃爽使用logistic函数模型建立了电压与时间的关系模型，但舍去了大量不一致的数据，导致误差急剧增大[9]。本文中，笔者利用C题数据[10]，通过非线性拟合、多元回归等统计手段，对电池放电数据进行分析，建立了任意电流放电曲线模型和剩余放电时间预测模型，并利用MRE的定义对模型进行了检验。

2 放电曲线建立与求解

2.1 各放电曲线方程的建立与求解

图1为同一批次电池在9种电流强度下放电曲线。在电流强度I下，放电初期电压不稳定，对预测产生影响。定义t0(I)为该电流强度I下的预测分割点。通过Matlab编程，得到不同电流强度下对应的分割点t0(I)和电池最大放电时间tmax，见表1。

图 1 不同电流强度下电池电压与放电时间关系曲线

表 1 不同电流强度下的时间分割点

[t0(I),tmax(I)]放电电压处于下降趋势，且放电初期电压下降平缓，放电末期电压下降迅速，放电曲线与抛物线趋势一致。建立电压与电流强度、时间的二元抛物线模型一：

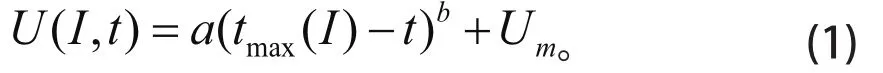
式（1）中，Um为额定的最低保护电压，本题中Um=9 V。结合表1，设定电流强度I，将式（1）转化为一元模型，利用Matlab软件进行非线性拟合，得出对应放电曲线系数，见表2。电流强度I下的放电曲线和放电电压的误差曲线如图2、3所示。拟合曲线与实验数据高度吻合，且电压的最大误差低于0.09 V，拟合效果好。

表 2 电流强度I下放电曲线系数

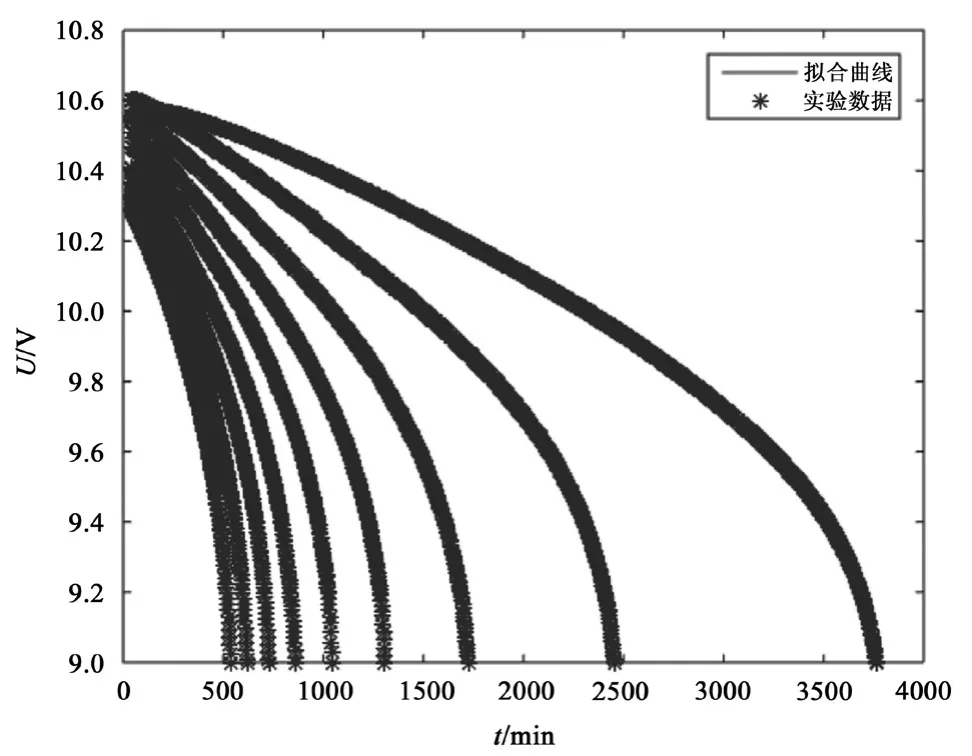
图 2 不同电流强度下的放电曲线

图 3 不同电流强度下的误差曲线

不同电流强度下的电压误差呈现出震荡趋势，建立误差函数

式（2）中，c、d、f、g为系数。结合式（1），改进模型，得出模型二：

以I=100 A为例，对误差函数系数进行拟合，得到放电曲线函数为：

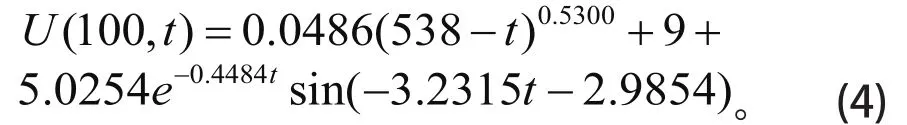
如图4所示，误差拟合曲线与模型一的误差曲线较吻合，误差曲线拟合较精确，从而提高了模型一的精度。特别地，U=9.8 V时，由模型一得出的电流强度I下的电池的剩余放电时间见表3。

图 4 I=100 A时的误差拟合曲线

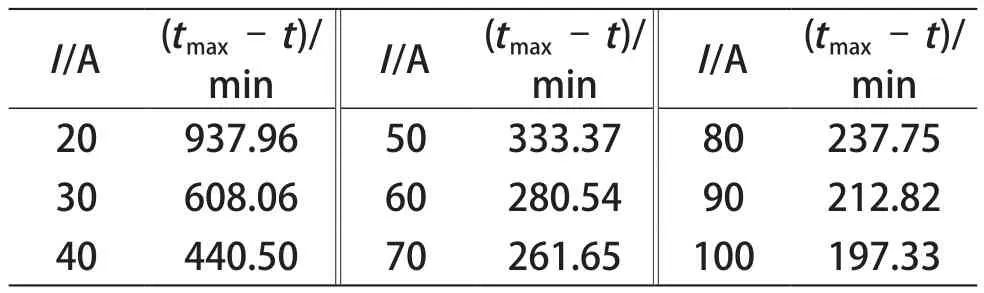
表 3 不同电流强度下电池的剩余放电时间

2.2 各放电曲线的 MRE 求解

注意到数据中电压间隔不同，且有部分超过0.005 V，利用三次样条插值，完善数据。根据平均相对误差（MRE）的定义[10]，按0.005 V的间隔提取231个电压样本点，计算出模型一和模型二下不同电流强度时的MRE，二者保持一致，见表4。MRE平均值为0.55%，最大值为0.96%，所以MRE整体较小，具有一定的优势[11-15]。通过计算，由模型二通过震荡函数调整放电初期的放电情况，降低了拟合的绝对误差，提高了拟合的精度，所以从此角度来看，模型二优于模型一。但是模型二所需参数较多，拟合难度大，且其对MRE的计算未产生多大影响，因此如果基于该角度，模型一较优。

表 4 不同电流强度下的MRE

3 任意电流强度放电数学模型

利用上述模型，做出电流强度I下的放电曲线。通过图5可知，不同电流强度下放电曲线趋势保持一致，符合抛物线模型，将式（1）的系数看作是电流强度I的函数，建立任意电流放电曲线模型三：

图 5 电流强度I时放电曲线

利用多项式拟合，通过不断改变多项式次数，寻求最优线性关系，得出系数a(I)、b(I)和最大放电时间tmax(I)与电流I的关系表达式：

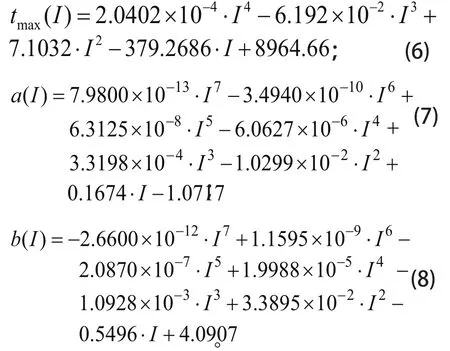
结合式（6）～（8），得出不同电流强度下的放电曲线函数的系数和最大放电时间。利用表5计算不同电流强度下的MRE，得到与表4相同的结果，表明任意电流放电曲线模型精度高。

表 5 电流强度I放电曲线参数

将I=55 A带入式（6）～（8），得出放电曲线方程为

对应放电曲线如图6所示。

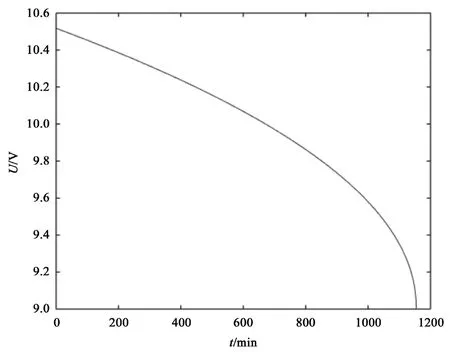
图 6 I=55 A时的放电曲线图像

4 电池剩余时间预测

设a=(a1,a2,…,an)为一个n维向量，amin为向量的最小值，amax为向量的的最大值，a*=(a1*,a2*,…,an*)为其进行标准化后的向量，则有

对电池在不同衰减状态下的放电数据进行标准化处理，得到如图7所示处理后的放电情况。三种状态下的电池放电状态趋势一致，建立衰退状态3下的放电时间t与新电池放电时间t1、衰退状态1下放电时间t2和衰退状态2下放电时间t3、电压u的多元回归模型四：

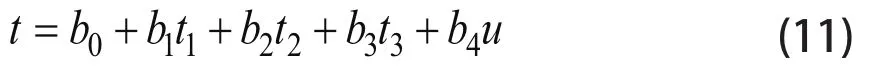
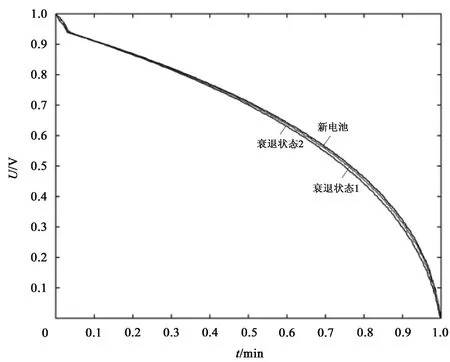
图 7 标准化后电池放电曲线

结合所给数据，利用Matlab进行多元回归分析，得出回归模型的统计量中R2为0.9999，F统计量值远大于分位点，检验P为0，小于0.05，表明该回归模型拟合优度高。对应回归模型的置信区间如图8所示。根据置信区间，剔除异常点的相关数据，建立自回归模型。经过多次回归，直至平均绝对误差不再减小，停止自回归，得到回归方程

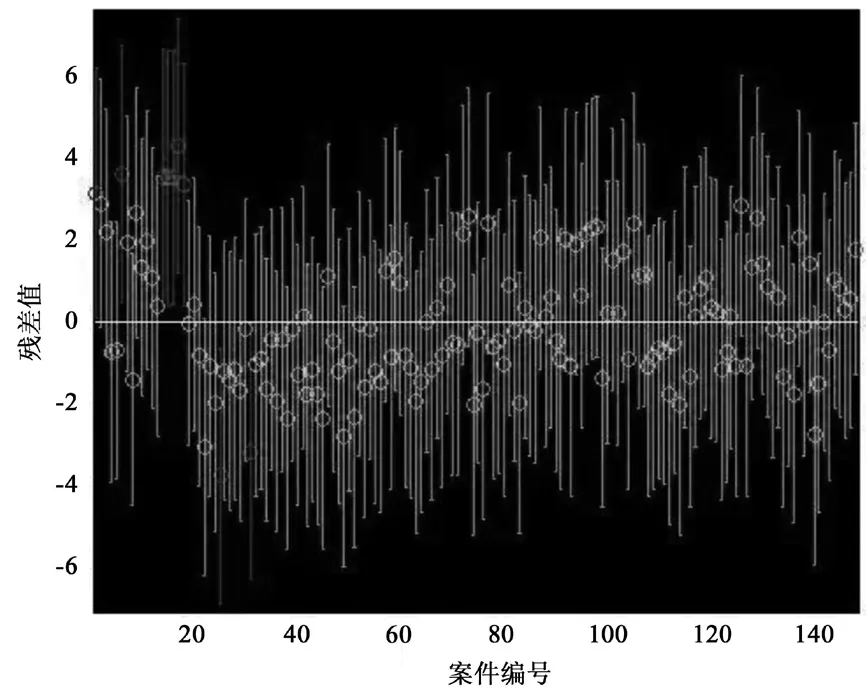
图 8 置信区间

模型的平均绝对误差为1.2867，表明拟合效果更好。衰减状态3下放电预测曲线见图9。利用该模型计算出衰减状态3的最大放电时间为836.37min，与当前放电时间596.20min的差为240.2min。

图 9 衰减状态3下放电预测曲线

5 结语

通过对放电数据的拟合，构建了任一恒定电流强度放电时的放电曲线模型。结合误差，增加误差震荡函数，对放电模型进行改进，解决放电初期的放电问题，且得到的MRE具有一定的优势。针对同一电池在不同衰减状态下以同一电流强度放电，对数据进行归一化处理，得出电池放电的共同规律，建立多元线性自回归模型，通过多次自回归，拟合出最佳的放电曲线。此模型具有通用性，只需将实际数据代入模型中，即可得出任意电流强度下的放电曲线，为电池性能的检测系统提供了有效的依据。