拉普拉斯变换在控制系统微分方程中的应用

周蓉，陈峰，严晨雪，王越群

（江苏商贸职业学院，江苏南通，226011）

0 引言

在没有人直接参与的情况下，自动控制（automatic control）是利用外加的设备或装置，能够使机器、参数、生产过程的某个工作状态或设备按照预定的规律自动的运行[1]。自动控制是一种技术措施，能自动调节、加工、检测的机器设备以及仪表，并给他们规定的程序或特定的指令，以便于让它们自动的作业。自动控制能够有效的增加产量、降低成本、提高质量，并且能够保障生产安全，确保工人的劳作强度等[2]。自动控制技术的研究有利于提高人们的工作效率，因此在一些复杂的环境中，人们工作的时间相对于以前降低了很多。自动控制技术利用了反馈定理，该定理利用输出信号反馈到输入信号，从而使输出值接近于我们想要的值[3-4]。自动控制系统中涉及到的基本的计算有拉普拉斯变换、傅里叶变换等。

1 拉普拉斯变换的概念

拉普拉斯变换简称拉氏变换，它广泛应用在许多科学技术和工程领域。研究过程中，我们需要从实际出发，首先以研究对象为基础，将其规划为一个时域数学模型，然后再借助于拉普拉斯变换数学工具转变为复域数学模型，最后如果想要结果表现的更直观，可以使用图形来表示，而图形的表示方法是以传递函数（复域数学模型）为基础，所以拉氏变换是古典控制理论中的数学基础[5-6]。利用拉氏变换变换求解数学模型时，我们就当作求解一个线性方程，换而言之拉氏变换不仅可用来将简单的时域信号转换为复数域信号，还可以用来求解控制系统微分方程[7]。拉氏变换是将时域信号变为复数域信号，反之，拉氏反变换是将复数域信号变为时域信号，下面对其概念作具体介绍。

■1.1 拉氏正变换

定义：对于定义在[0, ∞)区间上的函数f(t)，有拉普拉斯积分其中F(S)称作函数f(t)的拉普拉斯变换，简称为拉氏变换。

■1.2 拉氏反变换

拉氏反变换是拉氏正变换的逆运算，其公式为L−1[F(s)]=f(t)。

■1.3 拉氏变换的运算定理

在使用拉氏变换过程中，为了方便计算，常用到一些基本的运算定理，这些定理都可以通过拉氏变换定义式证明得到。

（1）线性定理

若L[f1(t)]=F1(s)，L[f2(t) ]=F2(s)，则L[k1f1(t) +k2f1(t)]=k1F1(s) +k2F2(s)。

（2）微分定理

L[f'(t) ]=sF(s) −f(0)， 在 零 初 始 条 件 下:L[fn(t)]=snF(s)。上式表明，初始条件为0时，原函数的n阶导数的拉氏式等于其象函数乘以sn。

（3）积分定理

在零初始条件下:L[ ∫ ···∫f(t)dtn]=F(s) /sn，上式表明，在零初始条件下，原函数的n重积分的拉氏式等于其象函数除以sn。

（4）位移定理

若L[f(t)]=F(s)，则L[e−atf(t) ]=F(s+a)。

（5）延迟定理

当原函数f(t)延迟τ时间，成为f(t−τ)时，它的拉氏式为：L[f(t−τ) ]=e−sτF(s)，上式表明，当原函数f(t)延迟τ，即成f(t−τ)时，相应的象函数F(s)应乘以因子e−sτ。

（6）终值定理

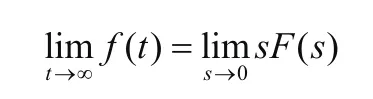
条件：sF(s)的全部极点除坐标原点外应全部分部在s平面的左半平面[8]。

2 应用拉氏变换求解微分方程

■2.1 求解微分方程步骤

拉氏变换求解控制系统微分方程的步骤如下：

（1）将微分方程转化为以s为变量的线性代数方程，该步骤利用拉氏变换。

（2）解代数方程得到输出量的象函数。

（3）利用拉氏反变换求出原函数即得到微分方程解[9]。

■2.2 实例1 拉氏变换求解电路微分方程

如图1所示RLC电路，试列写以ur(t)为输入量，已知输入为冲激函数，其中uc(t)为输出量的网络微分方程，利用拉氏变换求解uc(t)。

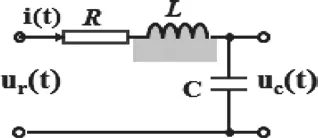
图1 RLC串联电路

由电路图可以看出，该电路是一个电阻电感电容串联的回路，因此流过该回路的电流相等，可以得出电容上的电流等于i(t)。根据电路图还可以看出，输出量为uc(t)，输入量为uc(t)，那我们只需要列出输出量和输入量之间的关系。其中，电感、电容是一个特殊的元件，电容上的电压与电流的关系式为：

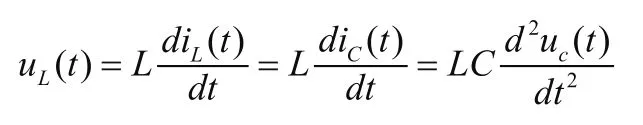
接下来我们根据基尔霍夫第二定律列出KVL方程：

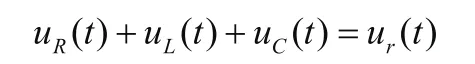
将数据代入上式：

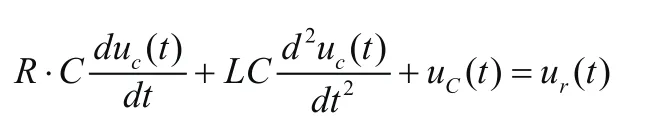
利用拉氏变换的微分定理列出上式变换后的式子：

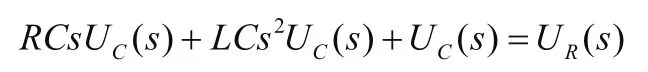
由于ur(t)为冲激函数，则其拉氏变换UR(s)=1，合并同类项，求出UC(s)：

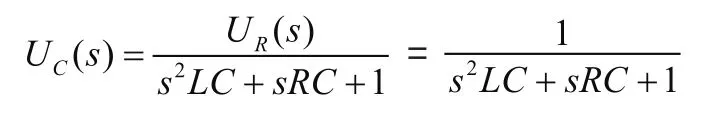
在这里为了方便计算，代入一组数据，令L=1H,C= 1F,R= 1Ω，得到UC(s)：

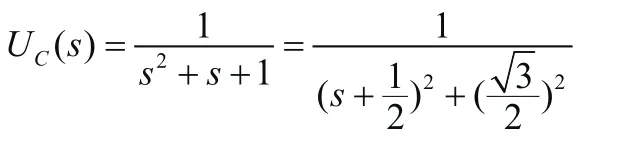
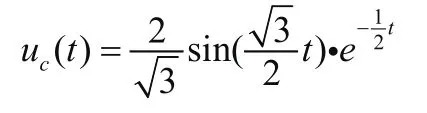
■2.3 实例2 拉氏变换求解机械位移系统微分方程

如图2所示为机械位移系统，图中所示k为弹簧系数，f为阻尼系数，F为外力作用，假设为阶跃函数，m是物体质量。列写质量m在外力F作用下位移y(t)的运动方程，并求出y(t)。

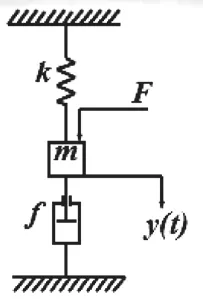
图2 机械位移系统

根据弹簧系数，考虑弹簧弹力2() ()Ft=kyt

根据力的平衡条件，列出平衡方程，得到外力F(t)，F3(t) =F(t) −F1(t) −F2(t)，代入后为：

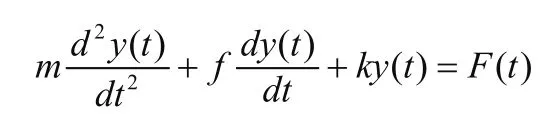
将微分方程转换为复域方程：

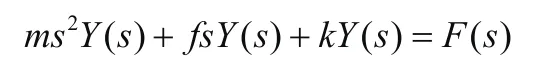
F(t)为阶跃函数，则其复数域函数为F(s)= 1 /s,代入上式得到Y(s)：

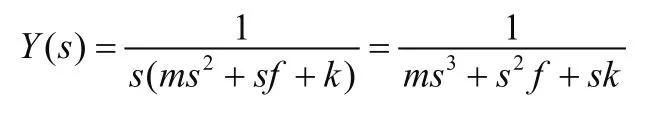
假设m= 1 ,f= 0 ,k= 0 ，得到，类似于抛物线函数，可得出其拉氏逆变换结果如下所示。

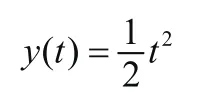
3 Matlab验证计算结果

■3.1 MATLAB的基本知识

自动控制原理的根轨迹分析、频域分析、时域分析、控制系统的设计等问题，要求数学基础扎实，对于抽象的一些问题，我们必须具备极强的想象力，比如在画Bode图、描述函数以及分析状态空间等一些问题时，要有能承受得住复杂、繁琐的计算与绘图的工具。使用MALAB编程运算可以说是模仿人在进行科学计算的思路和表达方式，所以说MALAB的语法更贴近人的思维方式，用MATLAB编写程序，运算求解问题，十分方便，就相当于在演算纸上排列书写公式。还有，MATLAB语言语句简单，极其容易学习与使用，并且MATLAB界面友好，使得从事自动控制的科技工作者乐于接触它，总而言之，MATLAB特别适合进行自动控制原理的实现。

■3.2 实例1 MATLAB验证拉氏变换求解电路微分方程

根据实例1中用拉氏变换求解电路微分方程，并且代入数据后得到接下来用MATLAB验证，最后仿真后得到的方程的结果如图3所示。

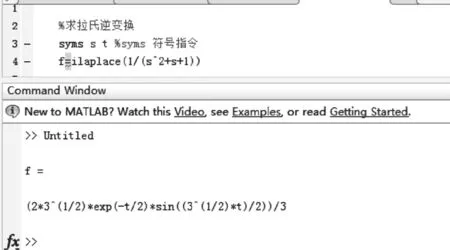
图3 实例1仿真结果

由此可见计算出的结果与仿真的结果一致。

■3.3 实例2 MATLAB验证拉氏变换求解机械位移系统微分方程

根据实例1中用拉氏变换求解电路微分方程，并且代入数据后得到，接下来用MATLAB验证，最后仿真后得到的方程的结果如图4所示。

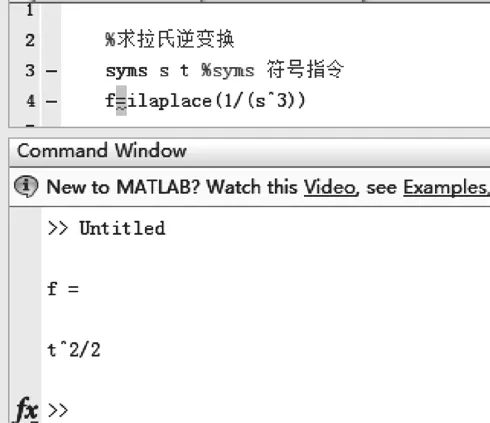
图4 实例1仿真结果

由此可见计算出的结果与仿真的结果一致，如果遇到比较复杂的式子时，利用MATLAB能更快更准确的仿真出结果。

■3.4 实例分析启示

根据以上的例题分析可以得到拉氏变换求解控制系统微分方程的基本步骤和方法为：分析控制系统，找出被控量→列出控制系统的时域微分方程→将微分方程拉氏正变换为复域方程→求解复域方程，得出被控量的复域函数→将复域函数拉氏逆变换得到微分方程的解。

4 结论

综上可知，学生学习时，如果遇到拉氏变换，教师需要用合适的方法来使学生对其加深印象。除了需要帮助学生分析系统的组成外，还需要帮助学生复习拉氏变换的基本定理及性质，这对他们以后学习的内容有相应的帮助，能让他们深刻理解其适用的对象及范围。并且，教师要重视典型例题的讲解、分析和总结，使学生在教学中掌握基本的定理，能够让他们灵活地运用这些定理。一旦学生有了独立分析问题的能力，这将对于增强他们发散性思维有一定的帮助。