混流式水轮机尾水锥管压力脉动的排列熵分析

2021-06-16付婧徐静张飞潘虹

噪声与振动控制 2021年3期

付婧，徐静，张飞，潘虹

（1.中国水利水电科学研究院信息中心，北京 100044；2.中国水利水电科学研究院科研计划处，北京 100038；3.国网新源控股有限公司技术中心，北京 100761；4.河海大学能源与电气学院，南京 211100）

混流式水轮机适用水头范围大致在50 m～700 m，是水电站中适用型式和范围最广的水轮机类型，单机容量在几十千瓦至一千兆瓦之间，适用功率范围宽广[1]，近年来，随着三峡、向家坝、溪洛渡等巨型机组的投运，以及后续乌东德、白鹤滩等电站的安装与调试，混流式水轮机正向高容量、大尺寸方向发展，水力稳定性所引发的机组稳定性问题越来越突出。混流式水轮机水力稳定性的激振源包括尾水管涡带[2]、卡门涡[3]、叶道涡[4]、转轮迷宫环间隙压力脉动[5]等。目前，对激振源的研究主要采用3种方法：采用计算流体动力学（Computational fluid dynamics，CFD）对内流场结构进行计算[5-6]，采用现场试验对稳定性参数进行观测[7-8]以及采用模型试验方法对压力脉动和内流场进行观测[9-10]。CFD方法受限于计算资源及精度方面的限制，而模型试验方法受限于比尺效应，因此这两种方法对压力脉动相关振源的研究不能完全真实地反映真机的问题。基于现场试验的压力脉动采集与分析则由于是对原型机组的真实测试，因此在故障诊断和状态监测中获得了广泛应用[11]。

针对压力脉动信号，如何进行特征提取从而获得水力因素对机组的影响一直是工程技术与科研人员亟需解决的问题，如：朱文龙等[12]利用支持向量机与极限学习机方法提出了基于水电机组运行工况的水轮机压力脉动诊断策略；蒲桂林等[13]考虑压力脉动信号的非平稳性提出了一种混合经验模态分解方法并应用于压力脉动信号分析中；贾嵘等[14]提出了基于二元树复小波特征熵的水轮机尾水管动态特征信息提取方法等。在包含水力、电气和机械因素的水电机组激励源中，水力因素所引起的机组稳定性问题最为突出，也占比最多[15]，而由于设计、制造以及运行中导致的尾水管内压力脉动则是水力激振的主要事故源，因而研究尾水管压力脉动特征对于水电机组状态监测具有非常现实的意义。

近年来随着信号处理技术的快速发展，涌现出了大量的分析信号的手段，其中用以表征信号复杂性的“熵”被广泛用于信号描述中。熵是信号复杂性的一种度量方式，对于给定时域信号，熵值的大小与信号的复杂性正相关，大熵值表明时序中所含信息丰富，复杂性强。常用的熵有排列熵（Permutation entropy，PE）[16]、近似熵[17]、样本熵[18]等。在众多熵中，排列熵基于信号自身，对信号没有任何假定，相较于其他熵具有对噪声鲁棒性强的优点，且算法简单，适用于处理大样本数据。因此，本文引入排列熵对全负荷工况（不同水头、不同负荷点）下某混流式水轮机尾水管压力脉动信号进行分析，建立了基于排列熵的机组稳定运行区评价方法。

1 试验基本条件

1.1 机组参数

某巨型电站安装有32台单机容量为710 MW的混流式水轮发电机组，基本参数为：额定出力710 MW，发电机额定出力840 MW，转轮直径10.44 m，同步转速75 r/min，最大水头113 m，最小水头61 m，额定水头85 m。

1.2 测试系统描述

为探索不同水位（工作水头）条件下机组的稳定性情况，分别在2008年和2010年试验性蓄水期间对厂房振动、机组振动和压力脉动等稳定性参数进行了测试。测试自上库水位145 m至175 m，基本涵盖了水轮机工作范围内的全部水头。本文主要对尾水管压力脉动进行研究，压力脉动测点布置：尾水锥管上、下游侧距转轮出口0.3D2处，如图1所示。除稳定性测点外，尚包括反映机组运行工况的工况参数，如工作水头、有功功率、导叶开度等。

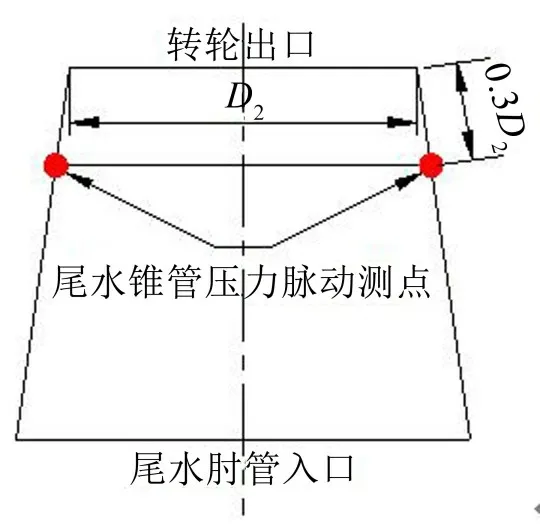
图1 尾水锥管压力测点布置图

压力传感器采用通用公司生产的PTX5072型传感器，精度为±0.2%，频响范围0～5 kHz（-3 dB）。功率取自机端出口计量用功率变送器，精度等级为±0.2%，采用计量电压互感器与电流互感器。

试验数据采集系统软件基于美国NI公司的LabVIEW软件平台开发，采用NI9205数据采集卡。采样精度为16位A/D，32通道总采样率可达625 kS/s，满足现场压力脉动数据采样需求。

1.3 工况调整方式

该电站下游尾水位在蓄水期间变幅较小，上库水位逐渐上升，为此上库水位每变化1 m进行一次变负荷试验。负荷调整方式：试验初始状态时，机组负荷调整到该试验水头下最大负荷（最大负荷不超过水轮机限制出力），阶梯降负荷到空载状态，整个过程持续时间约为10 min，连续采集信号；在升负荷过程中，为避免机组在部分负荷时机组不稳定工况持续时间过长，0～250 MW负荷区每50 MW调整一次，250 MW～500 MW每20 MW调整一次，大负荷区每10 MW调整一次。升负荷时待工况稳定2～3分钟后，对全部通道进行同步采样，采集时长为60 s，采样率为1 024 Hz。

2 排列熵

以嵌入维数m和时间延迟τ对时间序列{xt}t=1，…，T进行相空间重构得到：

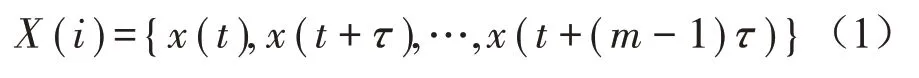
将X(i)的m个向量按照升序排列，得到一组新的序列S(g)={j1，j2，…,jm}，其中g=1，2,…，k，k≤m!。根据排列组合原理，这个序列共有m!种不同排列方式。然后计算每种符号序列出现的概率为Pg，则时间序列{xt}t=1…T的排列熵定义为

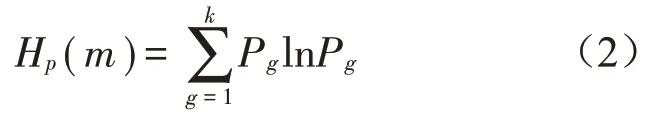
式(2)中，在Pg=1/m!时达到最大值，因此将排列熵进行归一化处理得到：

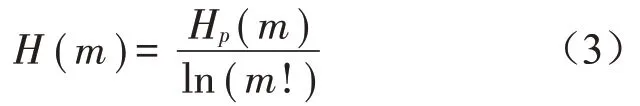
归一化后的排列熵范围处于(0，1]范围内，值越大表明信号所含信息量越丰富，信号的复杂程度也高，随机性越强。为进一步阐释排列熵概念，图2给出了处于涡带负荷区（520 MW）和稳定运行区（690 MW）的尾水锥管压力脉动实测数据时域波形图和频谱图，针对该组数据进行分析。

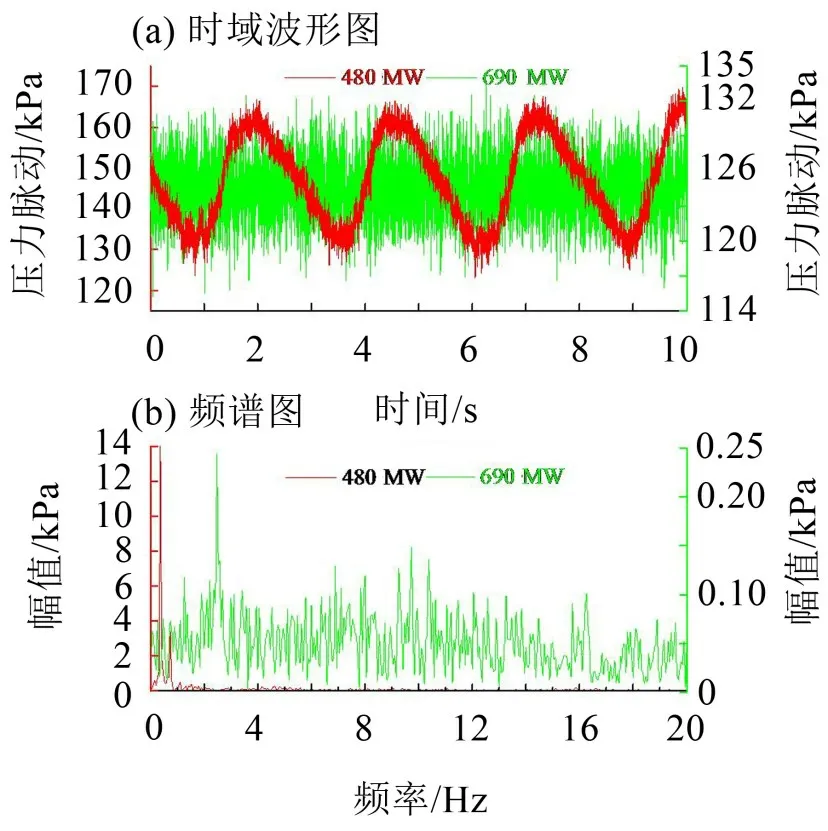
图2 典型涡带负荷区与稳定运行区的尾水锥管压力脉动

图2中，经计算涡带负荷区480 MW和稳定运行区690 MW时的尾水锥管压力脉动数据排列熵分别为0.634 5和0.829 0。引起不同工况下同一测点排列熵值区别的主要原因在于：涡带负荷区480 MW时锥管压力脉动受确定性的尾水涡带影响，其频率成分单一，考虑熵是信号信息复杂性的度量，因而在时域上确定性的信号中包含的信息量少，故熵值低；在稳定运行区690 MW时，锥管内流态好，信号中的压力脉动主要表现为随机的脉动频率成分，因而其频谱成分复杂，所包含的信息量大，故熵值高。

3 尾水管压力的熵特性

在应用排列熵对尾水管压力进行分析时，有两个关键参数对熵值计算结果产生重要影响：嵌入维数m和延迟时间τ。Bandt建议嵌入维数m在3～7之间[16]，m＜3时序列中的状态少，算法意义不明显，不能检测到序列中的突变。而当m太大时，序列将会均匀化，无法反应细微变化。为此针对具体工况进行分析，以确定合理的参数。

3.1 参数确定

嵌入维数m决定计算的复杂度。随着嵌入维数m的增大，计算的复杂性提高，造成计算速度降低，因此合理地嵌入维数m对于提高分析效率至关重要。延迟时间τ则体现了对数据的抽样程度。针对特定场景，很多文献均以仿真信号加白噪声等为例进行优化[19-20]，然而这并不能完全代表实际实际情况，为此本文对上游水位160.0 m，下游水位65.8 m，机组出力为710 MW时的尾水压力实际数据进行分析，其时域与频域波形图见图2所示，嵌入维数m选择为2～10，延迟时间τ为1～10，分析结果见下图3所示。

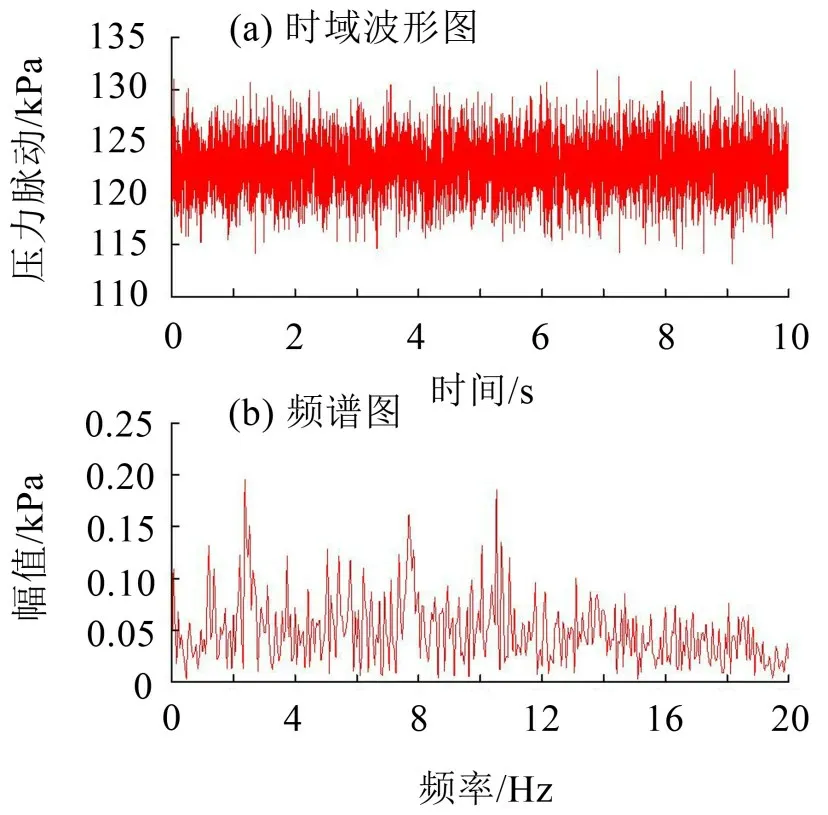
图3 尾水锥管压力脉动时域与频谱图

由图3可见，该组试验数据频谱呈现出一定的低频特性，没有明显的高频信号出现，总体上呈现出一定的随机性。由图4可见，不同的延迟时间τ，嵌入维数m与排列熵具有一致的变化规律，随着嵌入维数m的增大，排列熵值呈减小趋势；当嵌入维数m超过7后，排列熵值明显改变，且不依赖于延迟时间τ。以延迟时间为6为例，当嵌入维数从7到8时，排列熵值0.90减小至0.77，降低约14%，显著减小。考虑到排列熵值变化范围为(0，1]，因此较大的嵌入维数将导致排列熵值变化范围较小，不易于观察微小的信号变化。因此为获得较稳定且有一定变化范围的排列熵，嵌入维数m不应大于7。当m≤7时，随着延迟时间τ的增大，排列熵值有增大的趋势，以嵌入维数m=6为例，当延迟时间τ=1/3/5/7/9时，排列熵值分别为0.961/0.977/0.986/0.989/0.991，这表明延迟时间的增大使得信号呈现出某种程度的低频特征，这破坏了原有信号的分布特征，因此应选择较小的延迟时间τ。综合以上分析，本文选择嵌入维数m=6，延迟时间τ=3进行分析。

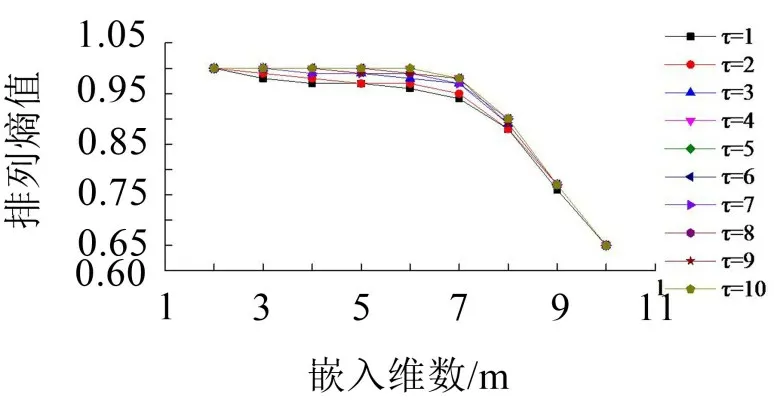
图4 案例数据嵌入维数与延迟时间的关系

3.2 定水头时的尾水管压力脉动排列熵特征

上库水位160.0 m、下库水位65.8 m时变负荷情况下尾水锥管压力脉动的排列熵值与混频幅值测试结果分别见图5和图6所示。图中测点1为尾水锥管上游侧压力脉动，测点2为尾水锥管下游侧压力脉动。

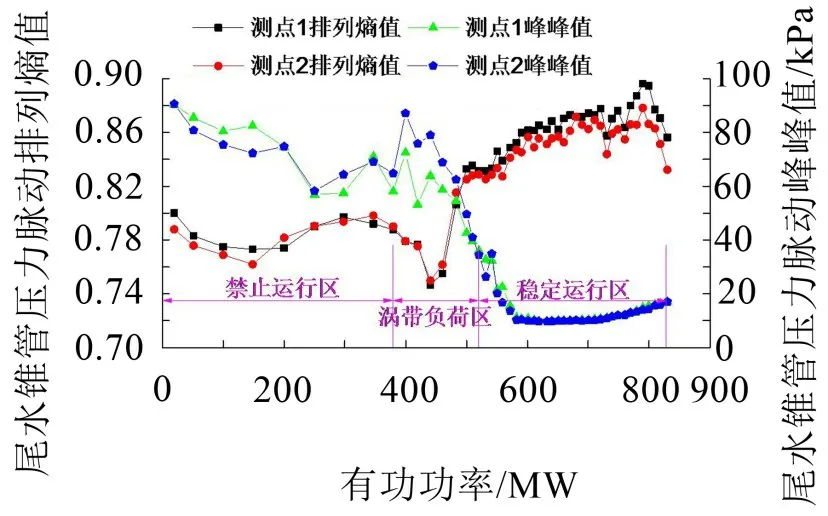
图5 尾水锥管压力脉动峰峰值、排列熵值与有功功率关系曲线

从图5可以看到：尾水锥管压力脉动两个测点的压力混频幅值和排列熵值分别具有相同的趋势，其中排列熵随着有功功率的变化近似呈“V”型分布，在大负荷稳定运行区排列熵值大于0.8，其它工况小于0.8；当负荷大于790 MW后，排列熵值突然减小，其主要原因在于当机组超负荷运行后，存在频率成分稳定的特殊压力脉动区[21]，该区域内压力脉动峰峰值有逐渐增大趋势；压力脉动峰峰值在小负荷区和部分负荷区较大，而在大负荷区（有功功率大于580 MW）较小，其中在大负荷区有略有增大的趋势。

分别计算两个测点的排列熵值与峰峰值的相关系数，其值分别为0.97和0.98，进一步表明两个测点的排列熵和峰峰值分别具有一致性；尾水锥管压力脉动上游和下游的排列熵与峰峰值的相关系数分别为-0.89和-0.94，这表明排列熵与峰峰值具有强烈的负相关性，因而可以作为表征水轮机工作状态的参数。目前，对压力脉动的评价普遍采用峰峰值评判，当进行故障诊断及异常分析时均需要对测点的峰峰值进行归一化处理，而排列熵本身即具有归一化属性，因此采用排列熵作为各种故障诊断系统的输入，从而可以替代归一化操作。然而，采用排列熵反映压力脉动的强度的机理有必要做进一步探讨。由于两个测点具有一致性，为此，研究人员以尾水锥管压力脉动上游侧为例进行分析。图6给出了该点的时域与频域谱阵图。时域信号中为了观测方便，将信号时长控制在10 s；由于压力脉动频域主要集中在低频段，故频域截止频率控制在20 Hz。

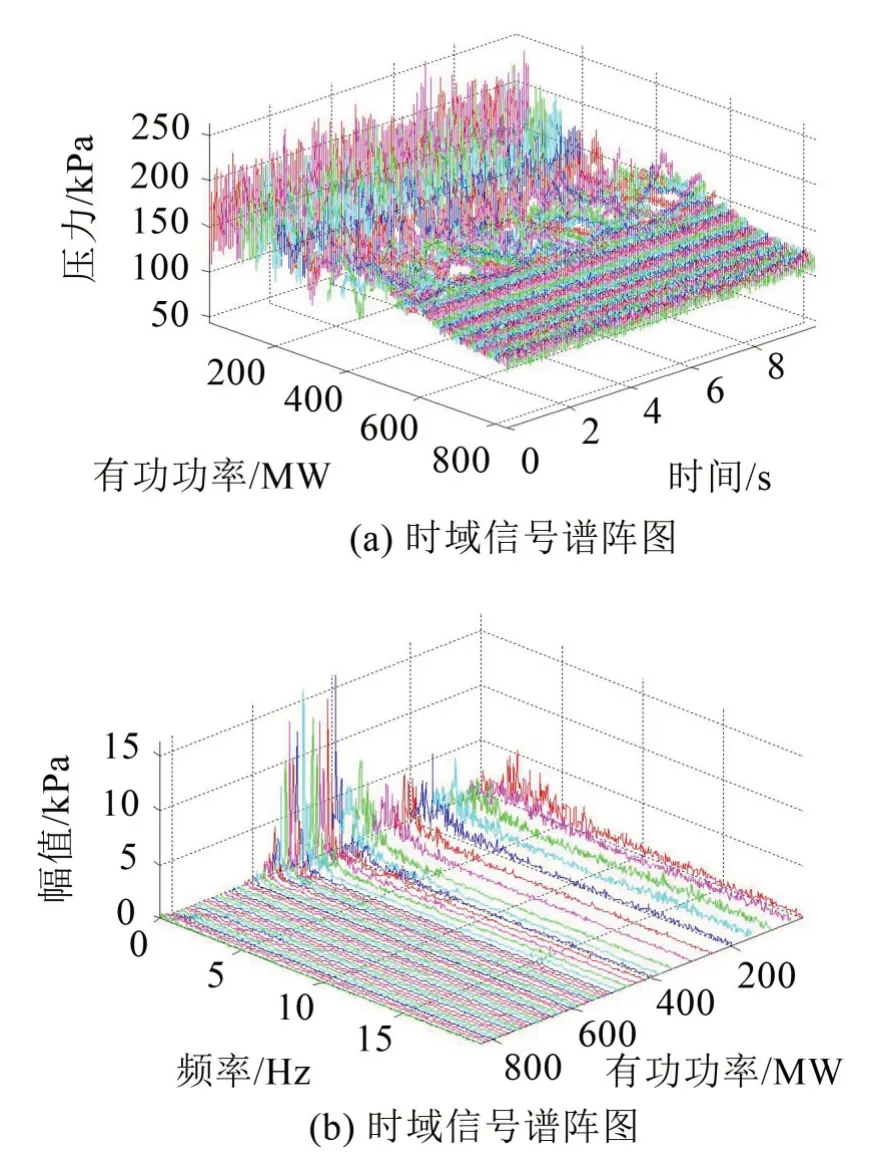
图6 尾水锥管压力脉动信号时域与频域谱阵图

从图6(a)中可以看出，随着负荷的增大，时域信号脉动与图5中的峰峰值一致，在涡带负荷区（380 MW～510 MW）之间达到最大值，此时对应排列熵有最小值（图5所示）；从图6(b)中可见：随着负荷的增大，机组由小负荷区向涡带负荷区和大负荷区逐渐过渡过程中，小负荷区时，尾水管内含有各种低频涡，信号中的低频成分脉动显著，表现为低频随机振动特性；涡带负荷区，频域中以尾水管涡带频率0.27 Hz为主频[2]，信号具有明显的周期特征；而在大负荷区段，机组进入高效区，尾水管内水流平顺，压力脉动信号具有明显的随机振动特性，幅值较小负荷区明显减小。

一方面，考虑到熵是信号中信息量多少的度量，对诸如含有明显主要频率成分的规律性信号，采样点的组合方式少，其含有的信息量也少，而对于随机信号，采样点的组合方式明显增多，频谱中没有显著的主频，含有的信息量将显著增大。另一方面，数据采集过程中，一般以加性噪声为主，噪声幅值不随传感器工作点的变化而发生改变。综合以上两个方面，相比较于含有明显主频信号的涡带负荷区尾水锥管压力脉动信号，大负荷区和小负荷区时，信号中由于没有明显的主频，表现为低频随机噪声，其含有的信息量明显增大，导致排列熵值较大。因此，尾水锥管压力脉动排列熵与负荷有直接关系，在一定程度上表征了运行时的机组稳定性情况，当机组无故障时，小负荷区和大负荷区排列熵值大，涡负荷区排列熵值小；有故障时，信号中将会产生明显的主频，信号的随机性减小，从而导致排列熵显著减小。

3.3 全水头下的排列熵

前述分析表明，排列熵反映了机组的实际运行情况，故可以采用排列熵对全水头（上游水位145 m～175 m）下的尾水锥管压力脉动进行分析，下图7给出了试验机组全水头下的该测点的三维等值排列熵图及其等值投影。

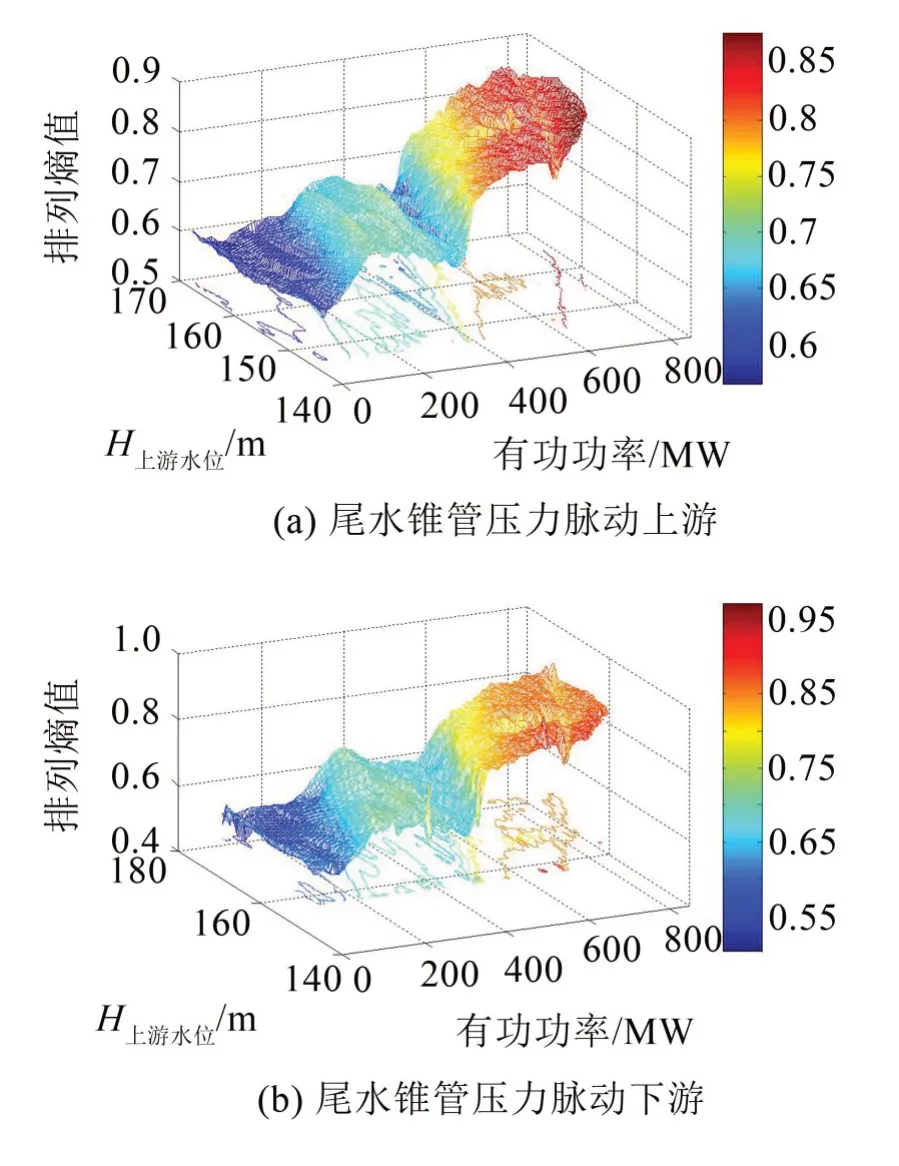
图7 全水头下尾水锥管压力脉动排列熵值图

图7可见：在全水头下，尾水锥管压力脉动两个测点排列熵值具有基本一致的变化规律；涡带负荷区和小负荷区排列熵值基本小于0.7，大负荷区则由于处于高效区，信号随机性增强，排列熵大于0.8。因此，排列熵值可以代表机组实际运行的工况。有必要指出，上述两个测点的排列熵是在机组无故障情况下获得的，一旦机组故障，则信号排列熵将明显发生改变，以此为参考作为故障诊断系统的特征数据输入，可以对异常工况进行诊断。