复杂声场下自适应LMS-VMT算法的研究

刘宋祥，陈仁文，张宇翔，丁学宇

（南京航空航天大学 机械结构力学及控制国家重点实验室，南京 210016）

有源噪声控制（Active noise control，ANC）一般分为全局有源噪声控制（GlobalANC）和局部有源噪声控制（LocalANC）[1]。全局ANC旨在减少整个目标声场中不需要的噪声。它的一个直接优点是：当ANC系统显著地对全局噪声进行控制时，用户能在体验降噪效果的同时，在整个声场中的移动不受限制。然而，在实际应用中，全局ANC系统通常不能将噪声衰减到可接受的水平，特别是在声模态密集的封闭环境[2]。相反地，局部ANC系统是利用在目标降噪点处的物理传声器采集的误差信号作为反馈来更新控制器的权重系数，最小化瞬时均方误差信号是系统的控制目标，即利用次级声源（通常为扬声器）使得物理误差传声器处的目标函数（通常是声压）达到最小。通过该系统，能在误差传声器处附近获得较好的降噪效果。

局部ANC系统的性能指标除了收敛速度和降噪量之外，还应涉及噪声控制的空间范围[3]。在局部ANC系统研究中，通常将降噪量为10 dB以上的区域定义为有效降噪区域[4-5]，称为“静区”。虽然在物理误差传声器位置处噪声可能会实现显著衰减，但“静区”范围往往非常小。此外，由于ANC系统的存在，“静区”外的声压级很可能会比原始干扰声压级更高。在实际应用中，例如座舱内部降噪，人耳才是感知噪声衰减的对象。因此，对于局部降噪系统产生的“静区”应该位于人耳附近。传统的局部ANC系统需要在目标降噪区域布置一个误差传声器，从实用性考虑，这大大影响了乘客的舒适性。虽然乘客可以佩戴有源降噪耳机[6]，但该方案的便利性较低。于是虚拟传声器技术（Virtual microphone techniques，VMT）被提出来用于解决以上的问题。

关于局部有源噪声控制的虚拟传声器技术最早由Elliott和David[7]提出来，他们提出了一种虚拟传声器布置方法（Virtual microphone arrangement，VMA），该算法建立在物理和虚拟传声器之间的初级声场变化较小的假设上，即认为它们的初级声压相等。但是该假设在很多场景下不能满足，例如声场的空间特性过于复杂或者物理传声器和虚拟传声器布置位置相距较远时，两者的初级声压将会有较大不同。于是，Roure和Albarrazin[8]提出了一种远程传声器技术（Remote microphone technique，RMT）对VMA方法进行改进。该方法在估计虚拟误差信号时，在物理传声器和虚拟传声器的初级声压信号之间引入了一个滤波器，提高了估计准确度。Cazzolato[9]针对VMA和RMT提出了另一种方法——前向差分预测技术（Forward difference prediction techniques）。在该方法中，使用前向差分预测理论确定每个物理传声器的权重，然后通过对来自阵列中的多个物理传声器的加权声压求和来估计虚拟位置处的声压[10]。为了克服前向差分预测技术中使用的物理传声器阵列之间的相位和灵敏度不匹配以及相对位置误差问题，Cazzolato[11]研究了使用自适应LMS算法来确定阵列中元素最佳权重的方法，称为自适应LMS虚拟传声器技术(Adaptive LMS-Virtual microphone technology，LMS-VMT)。在初步辨识阶段，将物理传声器临时放置在虚拟位置，然后通过LMS算法调整物理传声器权重，以便最佳地预测该位置处的声压。权重收敛后，将物理传声器从虚拟位置移开，并将权重固定为最佳值。

本文在复杂声场下对自适应LMS-VMT进行了研究，并在理想声场模型和复杂声场模型下将其和传统局部ANC系统相结合进行了相关仿真实验，在初步辨识阶段对最优权重离线辨识，噪声控制阶段则分析了不同声场模型下自适应LMS-VMT算法在虚拟位置的降噪效果。

1 基于LMS-VMT的ANC系统

采用虚拟传声器技术的ANC系统利用物理传声器测量的声压信号来估算虚拟传声器的声压信号，该虚拟传声器位于期望的最大噪声衰减位置（通常为人耳处），称为虚拟位置。局部ANC系统将最小化虚拟位置处的估计声压，使得“静区”能有效地从原来的物理传声器位置转移到虚拟位置[12]。显然地，虚拟传声器是虚构的，是一种“非侵入”式的传感器。

1.1 FxLMS算法

现有研究中，FxLMS算法及其改进算法是应用较为广泛的有源控制算法[13]。FxLMS算法的迭代过程为

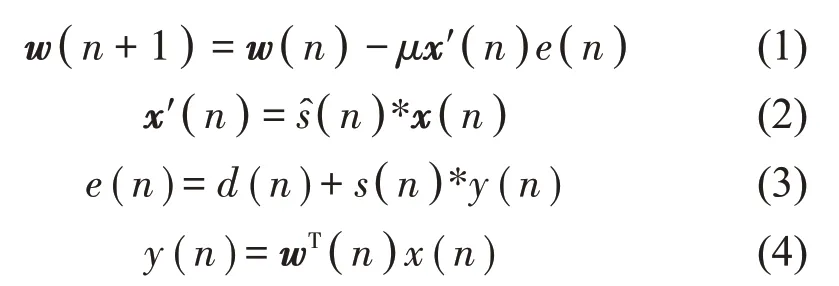
式中：μ为收敛系数；x′(n)为滤波-x信号向量为次级通道的估计的脉冲响应；s(n)为次级通道S(z)的脉冲响应；*表示线性卷积。

1.2 自适应LMS虚拟传声器技术（LMS-VMT）

自适应LMS虚拟传声器技术基本原理是利用LMS算法调整物理传声器阵列中各测量信号epi(n)的权重hi，如图1所示。然后通过这些信号的加权和得到虚拟位置的估计声压(n)，使得估计声压与实际声压ev(n)之间的均方差最小化。

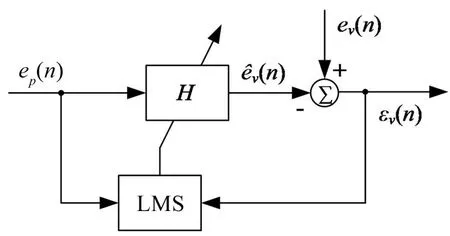
图1 自适应LMS-VMT算法基本原理框图

物理误差传声器的最优权重需要在初步辨识阶段来确定，通常将物理传声器放置在虚拟位置，然后关闭初级声源，并用带限白噪声激励次级声源。此时对于单个虚拟传声器，其虚拟输出误差为

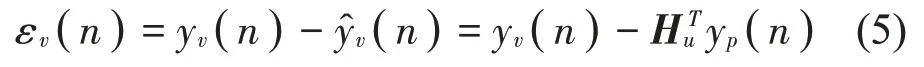
式中：yv(n)为虚拟次级信号(n)为虚拟次级信号的估计；yp(n)为物理次级信号。

物理传声器的权重Hu(n)的更新过程可由下式表示：

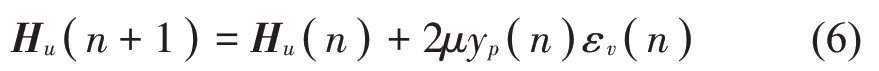
当输出误差εv(n)收敛时，此时的权重即为次级声场下物理传声器权重的最优值Hu0。对于给定物理次级声源，该权重对虚拟次级信号的估计是最佳的。

在实际控制阶段，虚拟误差信号的估计可表示为

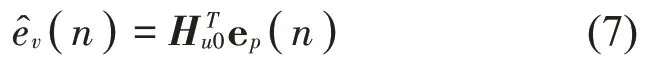
由于物理误差信号ep(n)=dp(n)+yp(n)，故式(7)可表示为

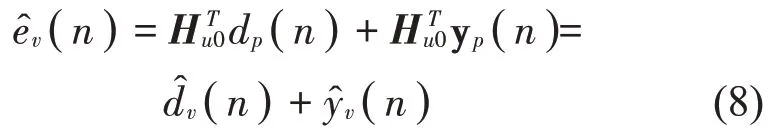
1.3 改进的LMS-VMT算法

式(8)表明次级声场的最优权重既适用于物理传声器的初级信号，也适用于物理传声器的次级信号。因此，LMS-VMT算法的基本假设为最佳权重Hu0对于虚拟位置的初级信号dv(n)和次级信号yv(n)的估计都是最优解。但这种假设对于较复杂的声场环境有较大的局限性。对于次级声源的近场，初级声场和次级声场的空间特性可能会非常不同[7]，这将导致次级声场的最佳物理传感器权重不能同时对虚拟初级信号和次级信号进行最优估计。因此，可以分别利用初级声源和次级声源获得初级声场和次级声场下物理传声器的最优权重，使得在较复杂声场环境下能获得对虚拟误差信号的最优估计。

利用物理传声器次级传递函数矩阵Gp（u初步辨识中估算），可以将物理误差信号ep(n)分解为初级分量dp(n)和次级分量yp(n)，即：

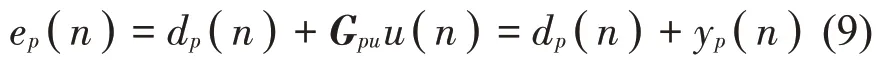
分别将初级和次级声场的最佳权重应用于物理传声器处的初级信号和次级信号，以便分别获得虚拟位置的初级信号和次级信号的最佳估计值(n)和(n)，将这些估计值叠加则可得到虚拟误差信号的最佳估计值(n)，即：

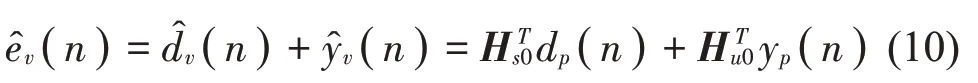
其中：Hs0为初级声场的最佳物理传感器权重；Hu0为次级声场的最佳物理传感器权重。

联立式(9)和式(10)可得：

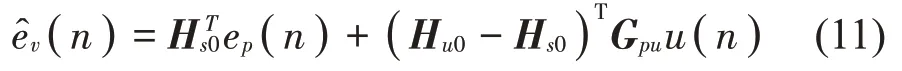
当虚拟位置处的初级声场和次级声场的空间特性相似时，即当两者的物理传声器最佳权重相等Hu0=Hs0=H0时，式(11)可表示为式(7)。

1.4 最优权重系数辨识

对于应用了LMS-VMT的局部ANC系统，如图2所示。有3个系统参数是未知的：虚拟次级通道传递函数Gvu、初级声场的最佳物理传感器权重Hs0和次级声场的最佳物理传感器权重Hu0。因此在实时控制之前，需要在初步辨识阶段进行系统辨识。根据激励的声源不同，可分别获得这些参数。进行系统辨识之前，需要在虚拟位置临时放置一个物理传声器，以获取虚拟位置的实际信号。

（1）辨识Hs0

将次级声源关闭，使用白噪声激励初级声源，利用LMS算法不断更新权重Hs，当输出误差εvs收敛时，得到的权重为物理传声器最佳权重Hs0。LMS算法的迭代过程为

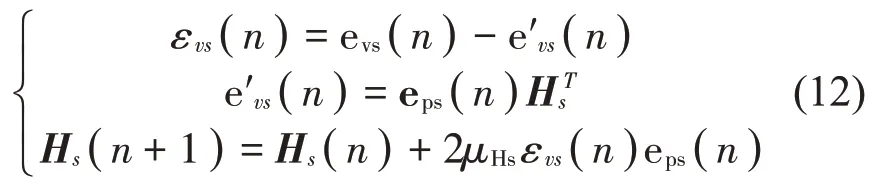
式中：eps(n)和evs(n)分别为物理传声器阵列采集的信号和临时物理传声器采集的信号，μHs为收敛系数。

（2）辨识Hu0和Gvu

将初级声源关闭，使用白噪声激励次级声源，利用LMS算法分别不断更新滤波器G权重系数和Hu权重系数，当输出误差ε′vu收敛时，得到的权重为物理传声器最佳权重Hu0；当ε″vu收敛时，此时的滤波器系数则为虚拟次级通道传递函数Gvu。权重Hu0和虚拟次级通道传递函数Gvu的迭代过程分别为式（13）和式（14）：

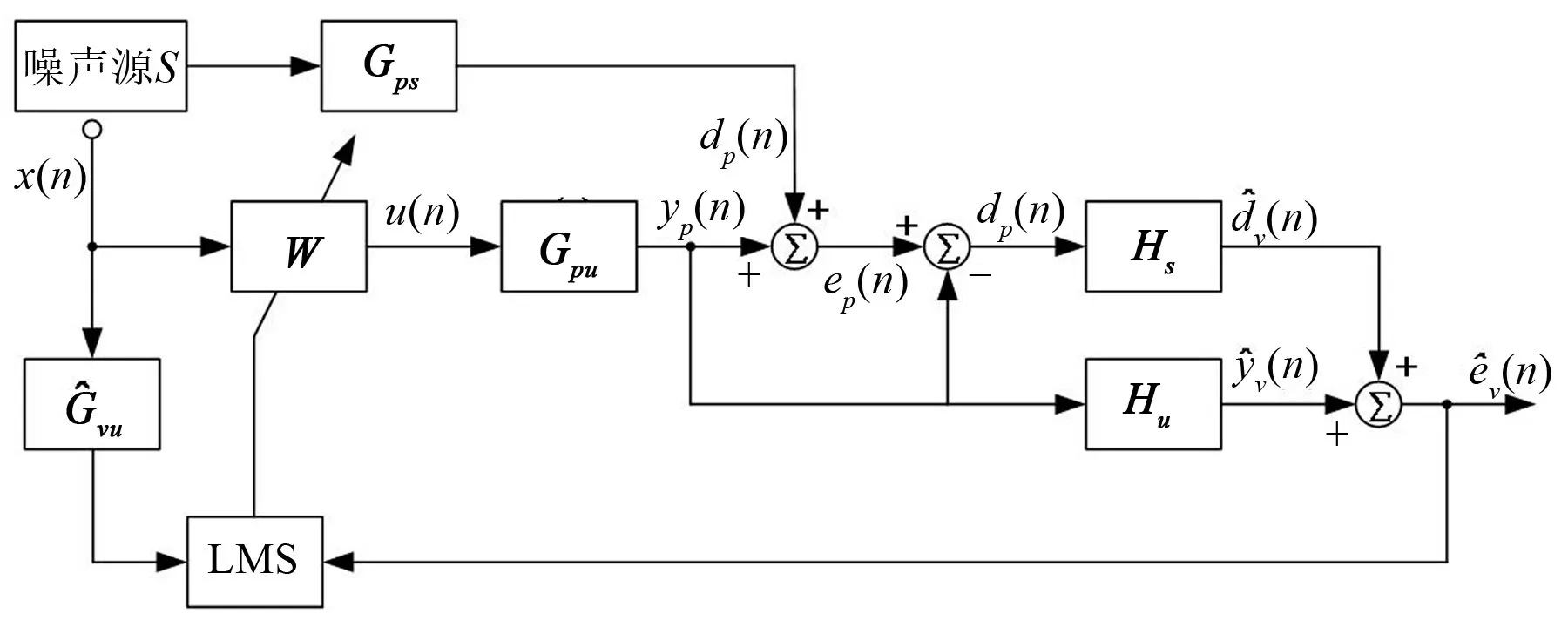
图2 基于改进的LMS-VMT算法的局部ANC系统框图

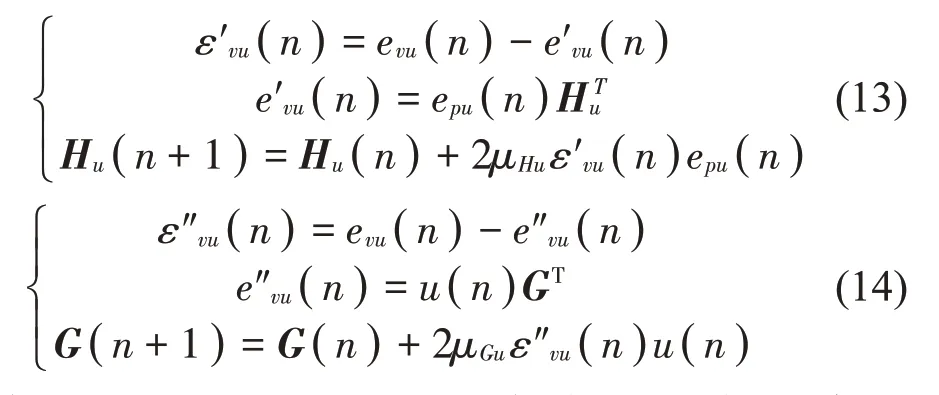
其中：epu(n)和evs(n)分别为物理传声器阵列采集的信号向量和临时物理传声器采集的信号；u(n)为次级声源输出信号，u(n)=[u(n),u(n-1),…,u(n-l+1)]T；l为滤波器G的长度；μHu和μGu为收敛系数。

2 仿真实验结果及分析

2.1 实验准备阶段

本文采用的模拟实验平台的示意图如图3所示。传声器阵列由5个物理传声器组成，实验中的声学仪器采用普通的扬声器和测试用的通用传声器。在该实验平台测得的通道数据的基础上，建立声学模型，对LMS-VMT算法进行理论分析和仿真。

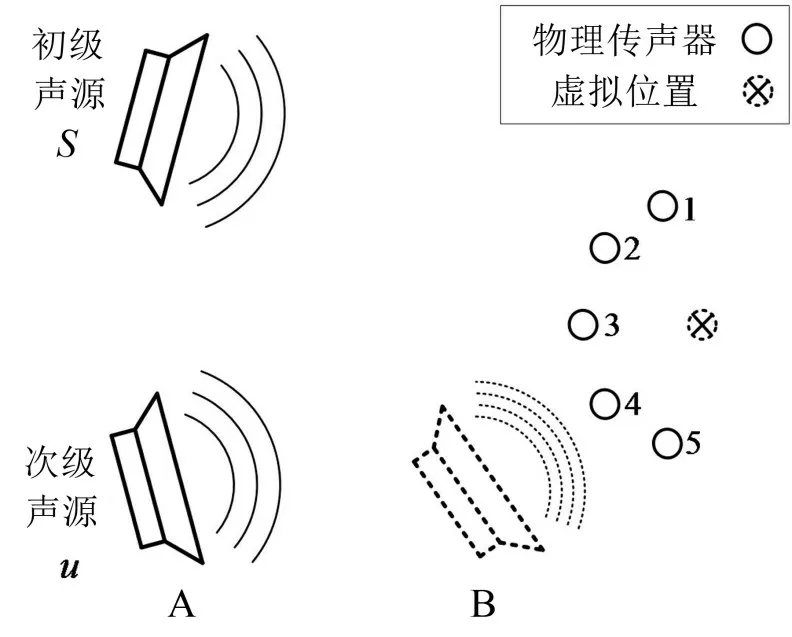
图3 模拟实验平台的示意图

通过改变次级声源的位置，设置了两组声场环境，当次级声源位于位置A时，分别激励初级和次级声源，再分别对每个物理传声器的通道模型进行辨识，可得到初级通道传递函数矩阵GpsA和次级通道传递函数矩阵GpuA；同样地，当次级声源位于位置B时，可获得GpsB和GpuB。

仿真实验根据图2所示系统框图进行设计。在本文中将基于GpsA和GpuA建立的声场模型称为理想声场，该模型满足LMS-VMT算法的基本假设，即初级和次级声场特性相似；基于GpsB和GpuB建立的声场模型称为复杂声场，用于模拟次级声源近场的声学环境。

实验采用虚拟位置处的噪声信号在时域上的功率比衰减（Power ratio decline，PRD）作为降噪效果的评估标准。即：

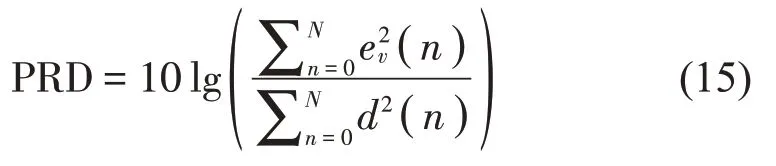
2.2 初步辨识阶段

在复杂声场模型下，根据1.4节内容进行初步辨识阶段。该阶段需要在虚拟位置放置临时物理传声器，用作采集虚拟位置实际信号。激励信号为白噪声，分别激励初级声源和次级声源进行辨识。当收敛系数μHs分别取0.005，0.01，0.05，0.5时，权重Hs的收敛曲线如图4所示。可知当μHs=0.05时，权重Hs收敛效果最好；当μHu分别取0.000 1，0.001，0.01,0.1时，权重Hu的收敛曲线如图5所示。其最优收敛系数为0.01；图6则为μGu分别取0.01，0.05，0.1，0.5时滤波器G权重系数的收敛曲线，由图可知，最优收敛系数取0.05。分析图4至图6可知，在一定的范围内，不同的收敛系数会影响系统辨识的收敛速度，但对辨识结果影响较小。

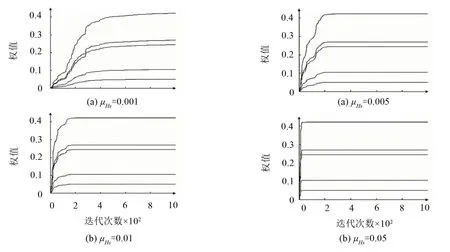
图4 权重Hs在不同μHs值下的收敛曲线

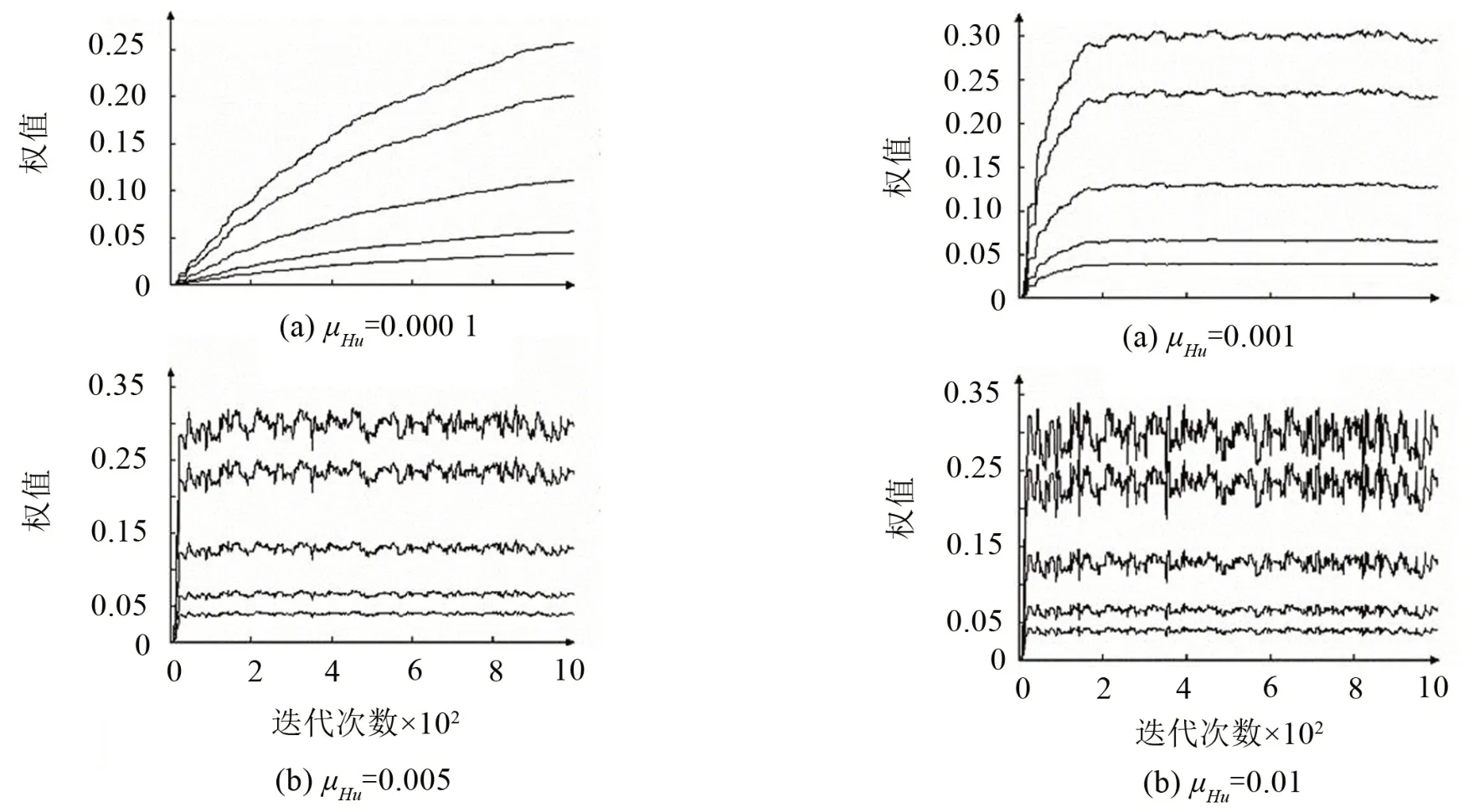
图5 权重Hu在不同μHu值下的收敛曲线

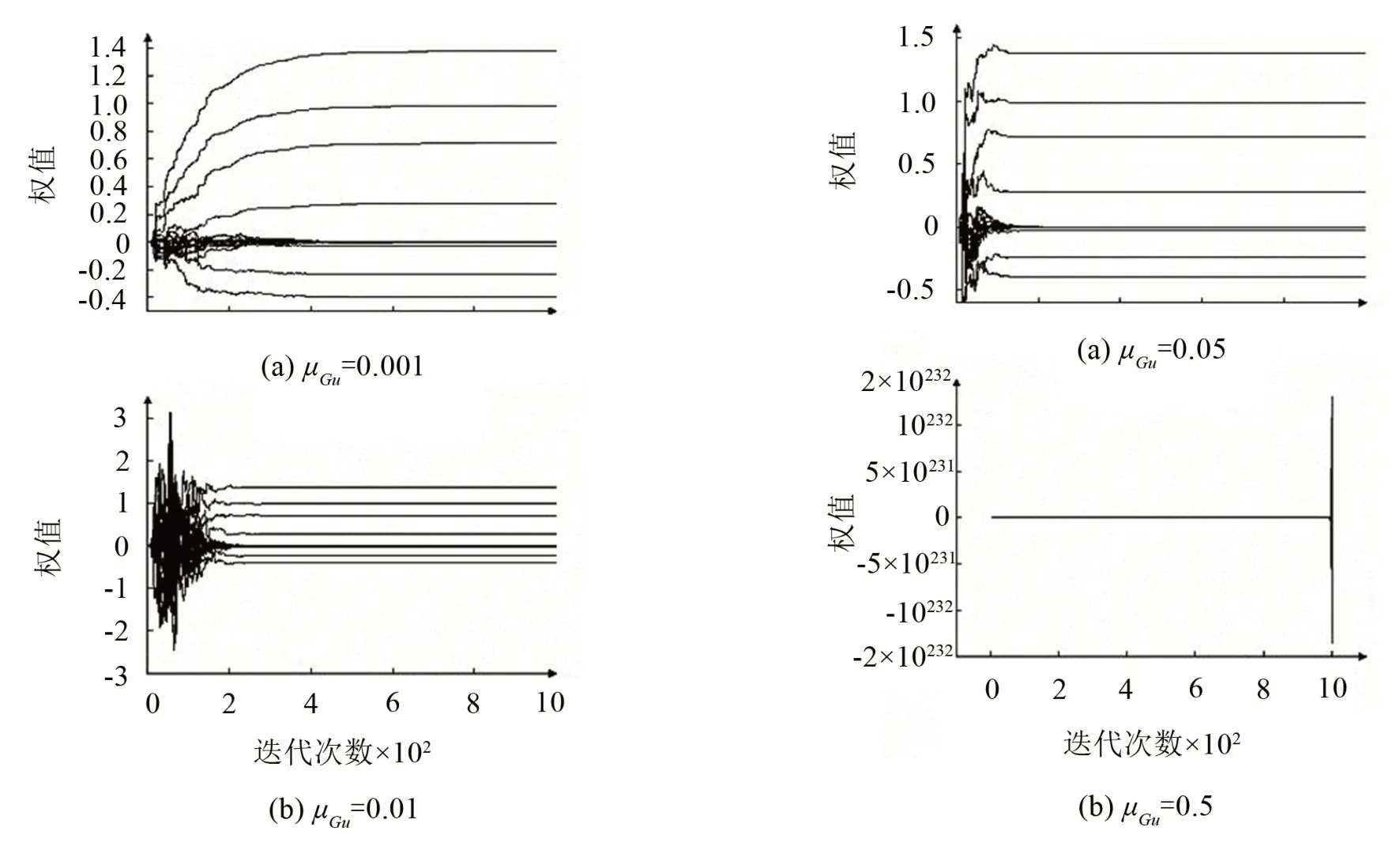
图6 权重G在不同μGu值下的收敛曲线

故取μHs=0.05，μHu=0.01，μGu=0.05来获得初级声场的最佳物理传感器权重Hs0、次级声场的最佳物理传感器权重Hu0和虚拟次级通道传递函数Gvu。

2.3 噪声控制阶段

将虚拟位置的临时物理传声器移除，将初步辨识阶段获取的Gvu、Hs0和Hu0在两组声场模型下进行ANC仿真实验。噪声源为采集的噪声，其采样频率为8 kHz。

实验中采用理想声场模型时，将FxLMS算法的收敛系数μ分别取0.000 05，0.000 5，0.001，0.005时，LMS-VMT算法和改进的LMS-VMT算法下在虚拟位置处的降噪效果对比如表1所示。

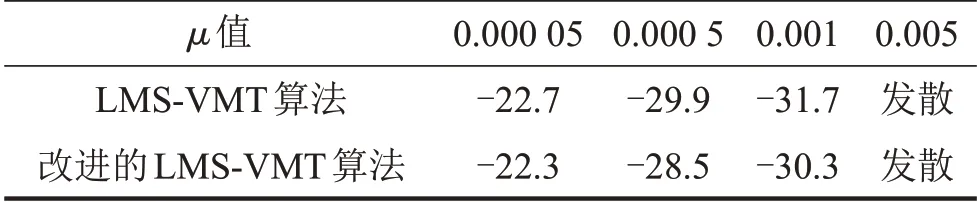
表1 理想声场模型中不同μ值下两种算法的PRD/dB

可知当μ=0.001时，两种算法在时域上的功率比均能下降大约30 dB。结果表明，在理想声场情况下两种算法都能使虚拟位置有较好的噪声抑制效果。

实验采用复杂声场模型时，同样将收敛系数μ分别取0.000 05，0.000 5，0.001，0.005，LMS-VMT算法和改进的LMS-VMT算法下虚拟位置的误差信号的收敛曲线如图7所示。由图可知，在一定范围内，μ值越大，收敛速度越快，当μ值增大到一定值时，系统稳定性将变差，甚至开始发散；当μ=0.001时，收敛效果最好。

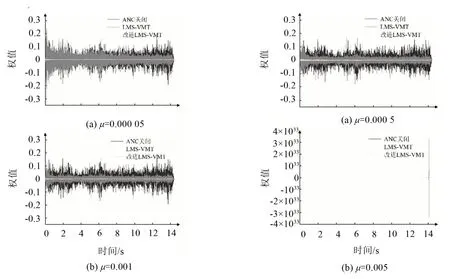
图7 不同μ值下两种算法的误差收敛曲线

图8为μ=0.001时，两种算法在时域的误差信号功率比的变化曲线，由图可知，在复杂声场模型下，采用LMS-VMT算法的ANC系统对噪声的抑制效果较弱，当ANC系统开启时，噪声信号没有立刻得到抑制，相反PRD升高了约15 dB；虽然随着时间的增加，噪声受到了抑制，但也无法达到理想声场模型下的降噪效果。而采用改进的LMS-VMT算法的ANC系统开启之后，噪声信号立刻得到显著衰减，功率比下降了25.8 dB左右。

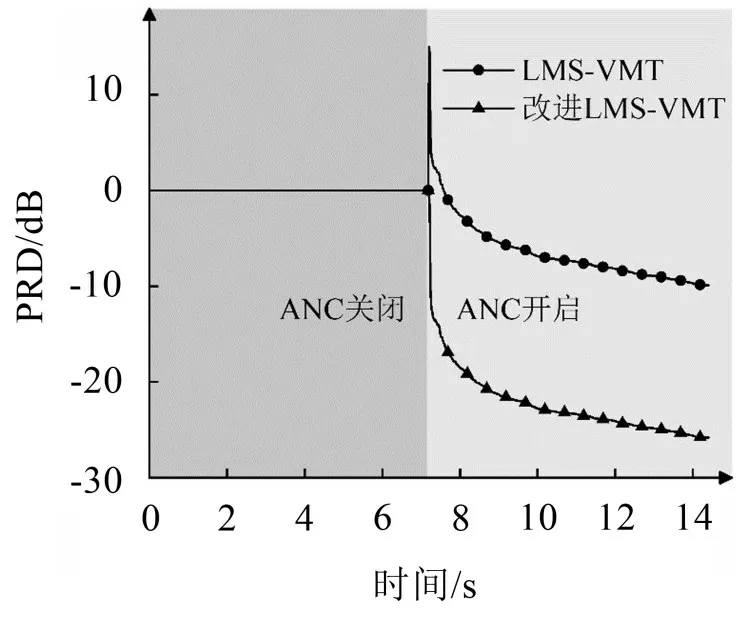
图8 μ=0.001时，两种算法降噪效果对比

3 结语

为了使得局部ANC系统的物理误差传声器可以远离目标降噪区域，本文研究了自适应LMS虚拟传声器技术（LMS-VMT），并根据次级声源近场的复杂性对其加以改进，同时研究了传声器阵列初级通道和次级通道最佳权重的辨识方法。在此基础上对系统进行了仿真实验，在初步辨识阶段分析了不同收敛系数对传声器阵列权重辨识结果的影响，并分别在理想和复杂声场模型下对LMS-VMT算法与改进的LMS-VMT算法进行了对比实验，结果表明LMS-VMT算法仅能在理想声场下具有较好的噪声抑制效果，而改进的LMS-VMT算法在两种模型下均能得到25 dB以上的噪声衰减。本文研究结果对ANC系统的实际工程应用具有一定的参考价值。