采用动态双子群策略改进的灰狼算法及其在心电信号识别中的应用∗

刘继忠谢毓顺徐文斌邓家诚李继发丁亚飞

(南昌大学,南昌市医工结合研究重点实验室,江西 南昌330031)

近20年以来,元启发式算法(meta-euristic algorithm)迅速发展,它是源自于自然现象的启发,并结合计算智能的机制求解复杂的优化问题最优解的方法,包括遗传算法(Genetic Algorithm,GA)[1]、模拟退火算法(Simulated Annealing,SA)[2]、粒子群优化(Particle Swarm Optimization,PSO)算法[3]、差分进化(Differential Evolution,DE)算法[4]、布谷鸟搜索(Cuckoo Search,CS)算法[5]等。

灰狼优化算法(GWO)是Mirjalili[6]于2014年提出的一种新型的元启发式算法。GWO算法与传统的PSO算法相比,其设置参数较少,编程难度小,且GWO算法本身并不依赖于参数的设置[7]。但GWO算法在求解高维度、多模态复杂函数问题时,容易陷入局部最优和出现早熟收敛现象。针对这些缺点,国内外学者提出了一些改进方法。龙文等人[8]在灰狼优化算法中引Powell局部搜索方式,有效提高了算法局部搜索能力。张悦等[9]在灰狼个体的适应度中引入了自适应调整策略和位置更新策略,提升了算法运行速度。Heidari和Pahlavani[10]提出一种高效的GWO算法用于处理全局优化问题,该算法利用Lévy飞行策略增强算法的全局勘探能力,引入贪婪选择算子加快收敛速度。Long等[11]分析了GWO算法的个体位置更新方程由全局最优解引导产生新个体,提出了一种修改个体位置更新方程以增强GWO算法的全局勘探能力。本文为了解决灰狼算法易陷入局部最优的缺点,将双子群策略引入GWO以改进GWO算法,并将其应用到SVM中,建立DDGWO-SVM模型,获取最优核参数和惩罚参数。并将改进后的SVM模型应用于心电信号识别中,提升了心电信号识别率,验证了该改进算法的寻优特性。

1 支持向量机基本原理

支持向量机(Support Vector Machine,SVM)是建立在统计学理论基础上的一种分类方法。依据结构风险最小化原则[12],通过选择的核函数将输入空间映射到高维特征空间,在高维空间构造最优分类超平面,并使分类间隔最大。以上问题等价于求解不等式约束条件下的二次规划问题。

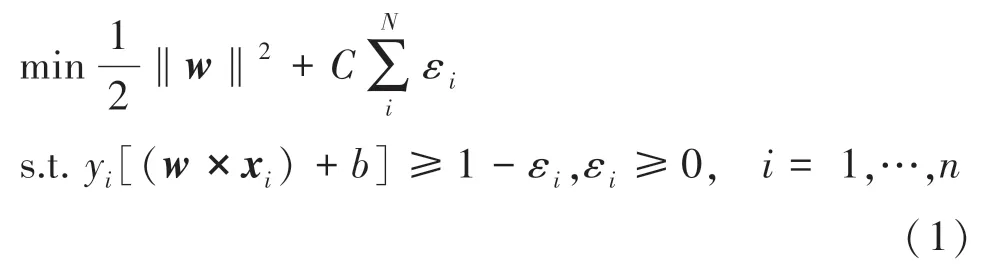
式中:C为惩罚因子,ε为松弛因子。对式(1)引入Lagrange乘子αi(i＝1,…,n)将该凸二次规划问题转化为对偶形式。

通过求解以上优化问题可以得到决策函数:

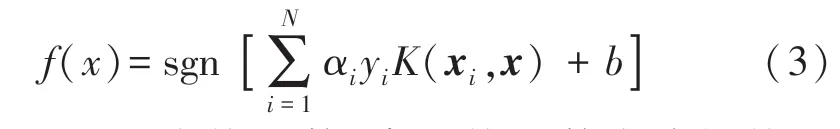
式中:K(xi,x)为核函数,常见核函数有线性核函数、多项式核函数等。本文选取泛化能力较强RBF核函数,其表达式如下:

根据以上推演过程可知,SVM模型的核函数参数g和惩罚因子C的不同取值,对SVM的分类性能有着重要影响。

2 灰狼算法

灰狼优化算法是通过模拟狼群的等级制度和捕食策略,以迭代的方式不断寻找最优值的一种群优化算法[13]。灰狼严格遵守着一个社会支配等级关系,其等级制度形如图1所示的金字塔式结构。根据灰狼种群中每个个体的适应度,将狼群中适应度最好的三匹灰狼,依次标记为α、β、δ,而剩余的灰狼标记为ω,GWO算法的优化过程主要由每代种群中的最好三个解来指导完成。

图1 灰狼群体等级

①包围猎物

灰狼群体围捕猎物时,需要确定猎物与灰狼之间的距离。它们对猎物的搜索行为可以通过如下公式进行描述:

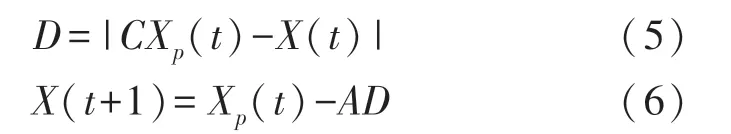
式中:Xp(t)表示第t代猎物的位置；X(t)表示第t代时灰狼个体的位置；常数C为摆动因子,由式(7)决定,A为收敛因子,由式(8)决定:

式中:a在迭代过程中从2线性减小到0；r1和r2是取值在[0,1]之间的随机向量。

②猎捕

在α狼的带领下,β狼和δ狼逐渐靠近猎物,可以依靠这三者来估计猎物的位置,尽量靠近这三只灰狼,也就可能离目标最近。对于每一只ω狼首先根据式(9)、(10)计算它们与α狼、β狼、δ狼的距离,然后由(11)综合判断灰狼向个体移动的方向,ω狼个体的移动方向由α狼、β狼、δ狼来决定。

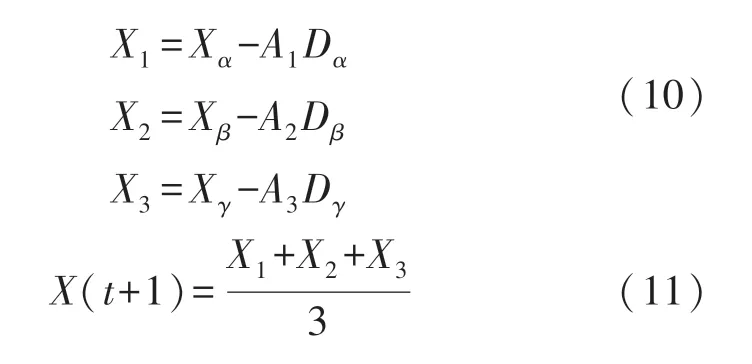
式中:X1表示α狼位置,X2表示β狼位置,X3表示δ狼位置,C1,C2,C3是随机向量。

当灰狼停止攻击猎物,捕猎行为结束,获得最优解。整个寻优过程通过式(8)中的收敛因子A在迭代过程中由2线性地减少到0来完成。当｜A｜>1时,在较大范围搜索猎物,对应全局搜索；当｜A｜≤1时,灰狼开始袭击猎物,对应局部搜索。

3 改进灰狼算法

标准的灰狼优化算法中(GWO)在解决复杂优化问题时,整个灰狼群体只向最优个体α狼靠近,种群迭代多样性随着迭代次数的增加逐渐减小,且如果该位置若不是全局最优,就会使算法陷入局部最优,出现早熟收敛的问题。实际上,种群在整个解空间中寻优时,全局最优解通常存在于局部最优的附近。适应度较高的个体有着较好的局部搜索能力,能够引导种群进行更加细致的搜索；而适应度较低的个体有着较好的全局搜索能力,能使种群避免陷入局部最优,故种群的进化速度更大程度取决于比较落后的个体而不是较优秀的个体。

本文借鉴文献动态双子群协同进化果蝇优化算法中的动态双子群策略[14],提出一种动态双子群策略灰狼算法(Dynamic Double-subgroup Strategy GWO,DDGWO),在迭代过程中,分别计算当前灰狼个体与α狼的距离Disti_best和当代最差个体的距离Disti_worst,若Disti_best≤(Disti_worst)/2,则将灰狼个体划分为以当代最优位置α狼为几何中心的较优子群；否则,将其划分以当代较差个体为中心的较差子群。根据两个子群的特点,采取不同的非线性收敛因子,以平衡局部搜索能力和全局搜索能力。

传统灰狼算法通过调整收敛因子a使灰狼种群在全局和局部搜索之间进行协调。标准灰狼算法的收敛因子a是呈线性递减的,难以较好的协调全局与局部搜索能力。本文提出对较优子群与较差子群采用不同的收敛因子,对于适应度值较高的较优子群,在迭代初期非线性收敛因子a1值快速减小,使得适应度较高的灰狼快速向最优解靠拢；迭代后期a1值缓慢下降以避免局部最优,a1如式(12)。而适应度值较低的较差子群,迭代初期a2值缓慢下降使得适应度较低的灰狼获得更大的寻优范围；迭代后期快速下降完成收敛,a2如式(13)。收敛曲线如图2所示,其中点划线表示较优子群的收敛曲线,虚线为较差子群收敛曲线,直线表示为标准灰狼算法的收敛曲线。

图2 非线性收敛因子

标准灰狼算法的ω狼在进行位置更新时,是由α狼、β狼以及δ狼共同决定,三只狼都是起着等同的指导作用,其并没有体现出α、β、δ狼在指导ω狼进行位置更新时的所占的比重,这种等同的指导会使得算法整体收敛速度变得缓慢。

本文采用一种基于欧氏距离的位置更新策略,通过式(9)中Dα、Dβ、Dδ倒数的占比作为权重系数,对灰狼个体位置进行更新,具体公式见式(14)。

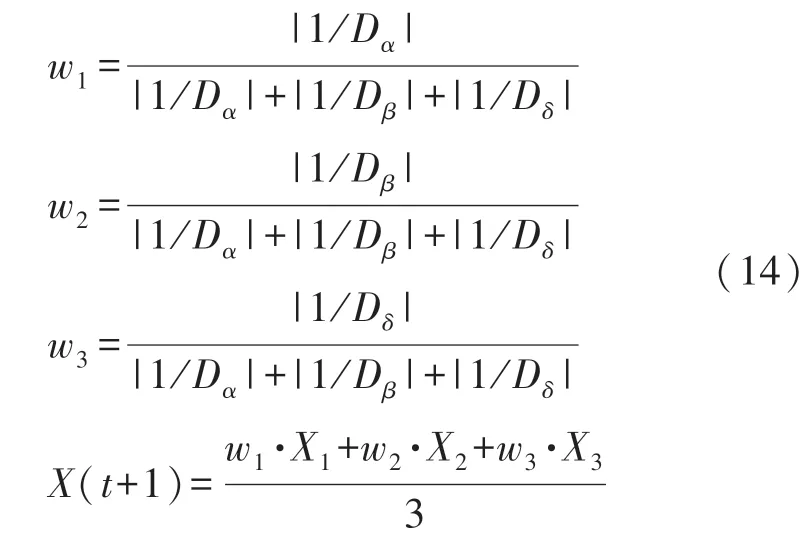
DDGWO算法流程如下:

①参数初始化,设置种群规模Sizepop,最大迭代次数Maxgen,初始化灰狼位置；

②遍历当前种群灰狼,计算适应度值；

③找出灰狼群体中的α狼(最优个体),以及适应度最差的ω狼(最差个体),分别计算并保留α狼的坐标Xa,Ya,以及最差位置ω狼的坐标Xw,Yw；

④利用式(15),分别计算灰狼个体i与灰狼群体中最优个体距离Disti_best以及最差个体距离Disti_worst:

⑤若Disti_best≤(Disti_worst)/2,则将灰狼个体i划分到较优子群,转步骤⑥；否则,将灰狼划分到较差子群,转步骤⑦；

⑥较优子群采用收敛因子a1及欧式权重,即式(12)、式(14),对灰狼个体位置更新；

⑦较差子群利用收敛因子a2及欧式权重,即式(13)、式(14),对灰狼个体位置更新；

⑧合并较优子群与较差子群；

⑨进入迭代寻优,重复执行步骤②到步骤⑧直至当前迭代次数等于最大迭代次数

4 实验分析

4.1 DDGWO算法性能测试

为测试DDGWO算法寻优性能,以表1中6个标准函数为测试函数,对本算法与标准GWO算法、基于LF改进灰狼算法(LGWO)[10]、探索增强灰狼算法(EEGWO)[11]、改进灰狼算法(IGWO)[15]、混合差分进化灰狼(HGWO)算法[16]进行对比测试。6个函数中F1～F3为单峰测试函数,F4～F6为多峰测试函数。三种算法的参数设置如下:种群规模均设置为30,最大迭代次数均设为500。测试函数在上述参数设置的条件下,为了避免单次寻优的偶然性分别独立运行30次实验,取平均值和标准差作为最终测试结果,其中LGWO、EEGWO、HGWO算法结果直接来源于参考文献[10－11,16],算法结果见表2所示。

表1 标准测试函数

表2 算法实验结果

由表2中的6个测试函数的运行结果来看,DDGWO算法在测试函数F1、F4、F6上均取得最优解,并且在整体性能上明显优于标准的GWO算法。F1～F3单峰函数测试结果表示DDGWO算法无论是在平均值或均方差上,均明显低于LGWO、GWO、HGWO和IGWO,相较于EEGWO的结果,两算法在F2、F3上各有优劣,均接近最优解,结果表明DDGWO算法对于单峰函数有着极好的优化精度。从F4、F5、F6多峰函数测试结果可以看出DDGWO算法获得了较好的寻优结果,表明相较于标准灰狼算法,在遇到局部极值时更容易跳出局部最优,与其他的GWO变体算法相比,只有EEGWO算法在函数F5上略胜与本文算法,但是在函数F6上DDGWO优于EEGWO。

总体而言,通过对6个基准测试函数的仿真实验,与5种优化算法作比较,实验结果验证了采用动态双子群策略能够有效提高灰狼算法的性能,在大多数情况,相较于标准GWO算法和其他先进的GWO变体算法,DDGWO有着更高的寻优精度和寻优稳定性,能够提供具有很高竞争力的优化结果,为GWO算法的改进提供了一种新的思路。

4.2 基于SVM的DDGWO算法心电信号识别分类

由于医学数据涉及到个人隐私,因此目前能够公开获取到的心电数据数量不多。而善于处理小样本的支持向量机(SVM)在处理心电信号问题上已经获得了不错的结果[17－18]。但是将SVM运用于实际问题中时,参数的选取对SVM的性能有着重大的影响,SVM的学习精度和泛化能力均取决于其参数优化选择。

为了进一步验证本文提出的动态双子群策略灰狼算法的优化性能,建立DDGWO-SVM模型,进行心电异常信号识别。将算法与灰狼算法(GWO)、粒子群算法(PSO)和布谷鸟算法(CS)优化的SVM参数寻优识别算法性能进行对比,并以分类正确率即识别率(Accuracy)作为评价指标。

实验数据采用MIT-BIH标准心电数据库[19]。取第一导联,以检测到的R波峰之前的99个点,之后的150个点作为一个完整的心拍,即每个波段包含250个采样点。从MIT-BIH心电数据库选取5类典型心电数据:正常的心电信号(NB)、左束支传导阻滞(LBBB)、右束支传导阻滞(RBBB)、心房早期收缩(APC)、心室早期收缩(PVC)。5类心电数据每类选取300个样本,共计选取1500个样本；其中每类取200个,共计1000个作为训练样本集；其余500作为测试样本集。5种类型心电信号具体如图3所示。

图3 5种类型心电信号

心电信号特征的提取采取小波变换法,与传统的时域特征相比,小波变换的多分辨特性,能够提取到更加有效的心电信息。MIT-BIH原始心电数据含有少量工频干扰、肌电干扰、基线漂移三种噪声。心电信号的主要频率集中在100 Hz以下,而90%的心电信号能量集中在0.25 Hz～35 Hz之间[20]。本文使用Mallat算法对ECG信号进行多尺度小波变换[21],采用对心电信号支撑性较好的‘bior2.4’小波进行8层小波分解。ECG信号经8层小波变换之后的频带范围对应关系如表3所示。

表3 小波分量于频带范围对应关系

肌电干扰、工频干扰主要集中在第d1、d2尺度,而基线漂移位于第a8尺度。对含噪声较多且有效心电信息偏少的d1、d2和a8尺度的子带信号不做处理,提取并计算其余尺度(d3～d8)频带能量,定义各尺度能量比作为心电特征,共取6个频带能量比作为SVM的输入特征向量,各尺度频带能量比具体计算方式见式(16)。

式中:Edi为第di尺度细节系数能量,Eai为第i层小波分解的近似系数能量。

设定各优化算法参数,其中CS算法的pa＝0.25。PSO算法的c1＝c2＝1.45,v＝0.9。DDGWO、CS、PSO、GWO算法的种群大小均为30,最大迭代次数为100,惩罚因子C与RBF核函数g的取值范围均为[10＾(－4),10＾4]。由于启发式算法具有一定随机性,在相同试验环境下,各算法模型分别独立运行10次,并进行对比分析,具体如表4所示。

表4 各算法模型10次独立试验分类结果

由表4可以看出,由于GWO与PSO易陷入局部最优,虽然也能取得较好的识别率,但模型稳定性较差。DDGWO-SVM模型相较于GWO-SVM和PSO-SVM模型,具有更好的识别率且识别稳定性更高。虽然相较于CS-SVM模型提升较小,但由于布谷鸟算法的全局寻优特性,算法收敛较慢,具体运算中同等环境下CS-SVM模型的运行时间为DDGWOSVM的两倍左右。由此可以看出,本文提出的动态双子群策略灰狼算法能够对SVM参数起到较好的优化,并且以DDGWO为基础所建立的DDGWOSVM模型对心电信号不但具有较高的识别率,且具有较高稳定性。

5 结论

为了解决灰狼算法易陷入局部最优的缺点,本文将双子群策略引入GWO算法,提出一种动态双子群策略灰狼算法,并用于SVM参数优化以检验其优化性能。基于6种函数的算法结果对比表明,与传统的GWO以及其他先进的GWO变体算法相比,DDGWO算法在单峰函数上具有优异的寻优能力,在多峰函数的寻优中,遇到局部极值时能够跳出局部最优,在大多数情况下拥有更高的寻优精度与更好的寻优稳定性,验证了所提出的DDGWO算法是有效的,进而为GWO算法的改进提供了一种新的思路。心电信号识别的对比实验结果表明,所提出的DDGWO算法能够用在SVM参数优化上,并且优化后的SVM模型对心电信号不但具有较高的识别率,且具有较高稳定性。