FHN神经元小世界网络随机共振下的弱信号增强∗

房 涛范影乐蔡哲飞武 薇

(杭州电子科技大学模式识别与图像处理实验室,浙江 杭州310018)

20世纪80年代Benzi等人在研究周期性复发的冰河期问题,发现在偏心率如此小的周期性下,地球的气候不足以发生这么大的变化,为了合理的解释这种现象,他们提出了双稳态的非线性气候模型,完美的解释了周期性冰河期的原因,并将这种现象称之为随机共振[1－2]。自此之后,随机共振吸引了大批学者的研究关注,同时为噪声与弱信号的处理提供了一种新的思路[3]。

随后,越来越多的学者在生物信号处理过程中也发现了越来越多随机共振的现象,例如密苏里大学的研究团队发现在水鳌虾尾扇感知细胞感知过程中随机共振效应[4]；Levin等在研究蟋蟀触须的感知细胞中,发现了外界合适的噪声干扰有助于提高蟋蟀对微弱信号刺激的响应[5]；Braun等则在实验的过程中,发现合适的噪声有利于鲨鱼神经细胞膜振荡信号的传播[6－7]；Stemmber等发现动物脑皮质的视觉神经对于方向感知的过程中,也存在随机共振现象[8]；Liljenström等利用计算机模拟了海马神经网络模型,发现了随机共振的类似现象[9]；另外,在2003年Mori等人首次在人脑视觉处理区域观察到了随机共振现象[10]。随着对这些随机共振现象不断深入的研究,一些研究者开始尝试应用随机共振现象解决一些实际问题,比如Moss等将随机共振技术运用于模糊图像信号的增强[11]；Morse等则运用随机共振现象提高助听器对输出共振峰频率的检测能力[12]。另外,一些研究人员们陆续也在诸如Hodgkin-Huxle(HH)神经元模型、FitzHugu-Nagumo(FHN)神经元模型、Integrate-Fire(IF)神经元模型以及离散的Rulkov神经元模型中也都观察到了随机共振现象[13－15]。关于这些在生物系统中已经取得的研究成果和潜在的应用,说明随机共振可能是神经信息感知、传递和处理过程的普遍现象和重要机制[16－17]。但这些过程多是基于真实生物系统的生理现象观察,或者出于简化模型计算的考虑,大多是基于单神经元非线性系统的模型建模,并没有考虑到生物神经元系统集群所带来的更加强大的表征能力、非线性拟合特性以及系统稳定性的作用,因此神经元网络中的随机共振现象并没有得到深入研究,在处理噪声与弱信号的强鲁棒性也没有得到深入的分析。

近些年来,复杂网络已经成为计算神经的研究热点之一,涉及物理学、生物学以及计算机科学等多个学科领域[18－19]；另外,复杂网络的模型也得到了丰富,例如陆续提出的规则网络模型、随机网络模型、小世界网络模型以及无标度网络模型等[20],尤其是越来越多的生理实验研究表明,生物神经元系统具有小世界网络特性[21]。因此,本文提出了一种小世界神经元网络构建思路,并尝试应用于弱信号增强。首先基于概率随机重连的方法构建小世界神经元网络,将改进后具有随机共振的非线性FHN神经元设置为网络节点,同时基于生物神经元间的信息传递特性,设计网络中互连神经元节点之间基于动态突触的信息流传递方法,最后根据对输入信号和输出信号互相关系数的实时计算,舍弃互相关系数过低的异常输出节点值,提出了小世界网络有效神经元节点的输出信号均值融合方法,可以有效提高网络系统随机共振的鲁棒性,避免网络系统中单个神经元的异常输出,降低了弱信号的复原误差,最后通过对周期弱信号和非周期弱信号的实验证实了本方案的可行性。

1 基本原理

动物脑皮质的视觉神经生理实验发现随机共振可以有效地增强视觉信息,并能强化生物的视觉感知能力；随后在以HH模型以及FHN模型等简化模型为代表的神经元动力学模型上开展了较多的神经计算仿真研究[22]。因此在单个神经元意义上的随机共振已经得到深入广泛的研究,其研究成果已经应用在众多领域,比如图像增强、故障信号检测等等。但必须要指出的是,为有效提高系统的鲁棒性,神经元在大脑中往往是以集群形式工作[23]。

因此,本文从生物神经生理机制的角度出发,提出了基于概率随机重连的小世界神经网络构建方法,以FHN神经元模型作为网络节点,但改变了FHN神经元慢特征和膜电位特征时间参数保持一致的传统思路,从而可以灵活地改变膜电位势函数势垒以提高势阱间的跃迁概率；同时考虑到网络中神经元节点之间具有受时空调制的动态突触连接关系,因此本文提出基于距离连接权重的动态突触神经元节点信息流传递方法；最后为了有效而且准确地利用网络节点输出信息,通过实时计算输入信号和输出信号的互相关系数,舍弃互相关系数异常的节点输出信息,提出了一种网络节点均值融合策略对神经元节点输出信息融合。在合适的输入信号和噪声信号下,可以达到输入信号、噪声与FHN神经元节点的随机共振实现弱信号的增强复原,并通过调节网络中FHN神经元节点的内部噪声实现神经元群的同步放电,避免了单个神经元节点信息的输出不确定性,实现对含噪声弱信号的有效增强复原,具体的系统原理结构如图1所示。

1.1 FHN神经元随机共振特性

FHN神经元是在Hodgkin-Huxley模型的基础上简化得到的,尽管非常简洁,但却反映了神经元的本质特征,通过非线性正反馈膜电位描述“再生自激”现象,非线性反馈门电压描述恢复过程,可以模拟神经元的大多数特性。Longtin等利用FHN神经元模型对小龙虾神经系统的随机共振现象进行了研究,并取得了较好的实验结果。其具体形式如式(1)所示:

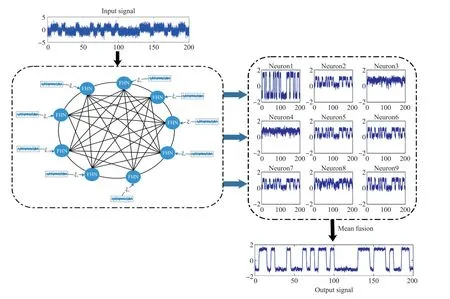
图1 系统结构图

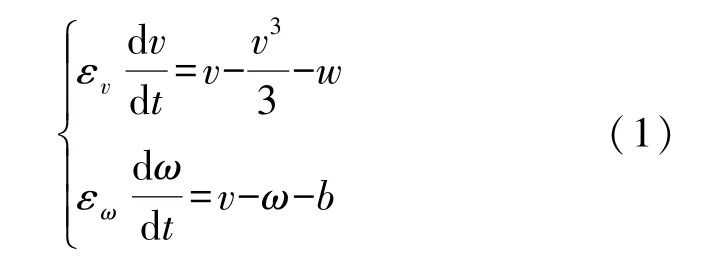
式中:v表示快变量即神经元的膜电位,ω表示恢复变量,b表示无量纲的正数；εv、εω分别表示膜电位和恢复变量的特征时间,传统模型为了简化计算过程,通常假设上述两个特征时间为同一数值。为了更加灵活地改变膜电位势函数势垒以提高势阱间的跃迁概率,本文对膜电位和恢复变量的特征时间进行独立设置,从而在相同的模型结构情况下,获得更为丰富的动力学行为。

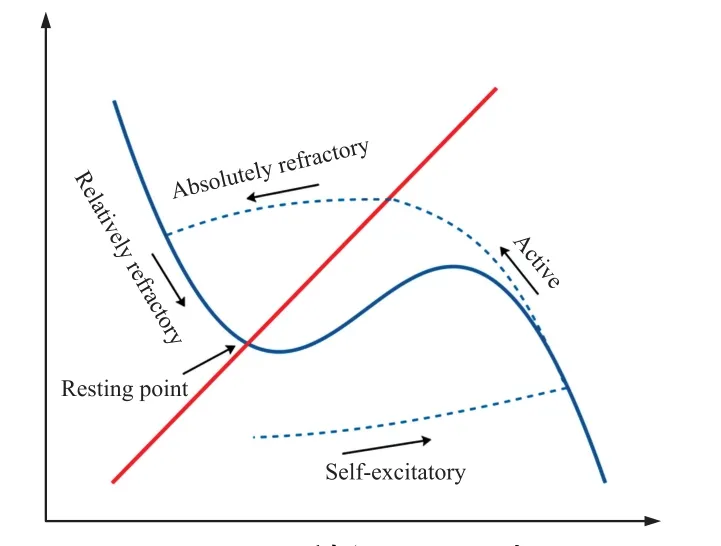
图2 FHN神经元v－ω相图

如图2所示,本文通过对FHN神经元v－ω相位图以及膜电位势函数的动力学特性分析,发现FHN神经元的相图主要涉及三个区域分别是震荡区域、双稳态区域和兴奋区域。在震荡区域内,状态点将随着极限环移动；在兴奋区域内,神经元出现了脉冲发放；双稳态区域内,状态点将会缓慢地回到某个稳定的稳定点。根据v－ω相位图可以发现,初始时刻状态点开始迅速地移动到立方零斜线的右侧分支,然后沿着右侧分支向上达到立方零斜线的局部最大值,完成一次动作电位的发放；接着状态点沿着立方零斜线上侧转化到左侧分支,系统的动力学是不稳定的,处于绝对不应期,在任何刺激下都无法产生动作电位；最后,状态点回到稳定点,在这段时间里处于相对不应期。通过根据式(2)定义势函数V,即

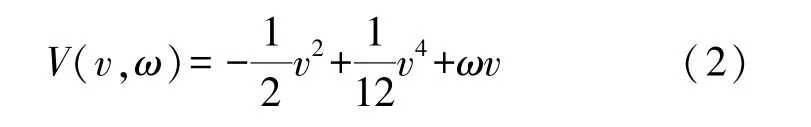
由于εv≤εω,ω在式(2)中的时间尺度下可以视为一个常量,在定点处,电压常数方程可以是仅含v的方程,势函数V的具体形状如图3所示,可以发现两侧的势阱是非对称的,这更有助于FHN神经元非线性系统,在外界弱信号的驱动下,在静息态到激发态跃迁；同时势垒的高度也可以通过调节参数b来调整,该性质可以实现随机共振的自适应响应。

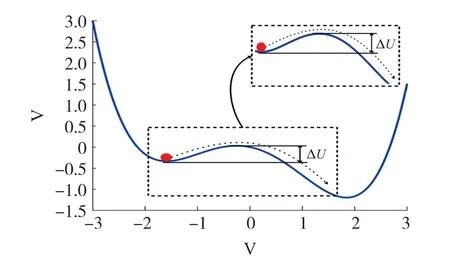
图3 势函数示意图

通过分析可以发现FHN神经元具有很好的非线性特性,在外界的信号的驱动下,可以实现不同势阱间的跃迁,这有利于对不同能量态的弱信号进行筛选,以实现信号的增强与复原。但对由于单个神经元的鲁棒性和系统的可表征性能都存在一定的缺点,因此受大脑的神经系统网络机制启发,本文提出通过概率随机重连的方法构建小世界神经网络,提高系统的稳定性。

1.2 WS小世界网络

在人类的大脑内,神经元之间通过突触连接构成了复杂的神经元网络,以此实现各种各样的功能。近些年,通过对大脑大量的生理实验,发现生物神经元之间具有小世界拓扑结构特性,这表明复杂的神经元网络的各个节点之间并没有很复杂的连接通道,相反,他们只有很少的连接间隔。基于这种特性,我们构建一个以FHN神经元为节点的小世界网络,各个节点之间具有如下规则,网络中的任一FHN神经元节点以及顺时针连接最近节点的边,通过设置节点之间的重连概率p,重新建立此节点与网络中任意其他节点的连接,且不允许和已经存在的连接重合,沿着网络的顺时针方向不断的重复这个过程,建立基于概率p的连接。通过设置不同的连接概率,可以得到不同复杂程度的连接网络,设置了一个节点数为20,每个节点与相邻的4个节点互联,与其他节点连接概率p分别设置为0、0.2、1,具体如图4所示。

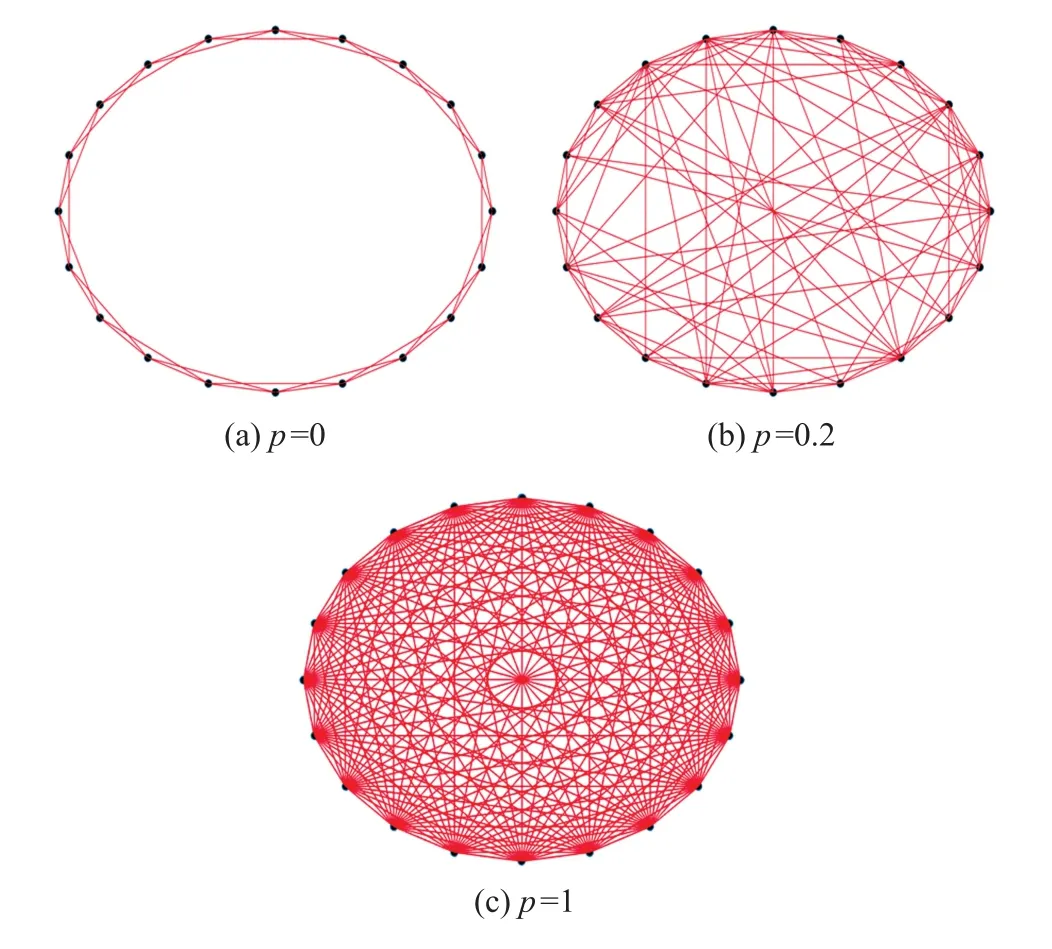
图4 小世界网络示意图

本文在Strogats和Watts提出的小世界网络结构基础上[24],提出使用概率随机重连的方法构造一个包含20个FHN神经元节点,重连概率为0.2的小世界神经网络,其动力学方程的具体形式如式(3)所示:

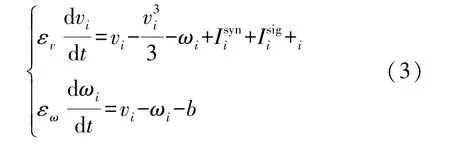
式中:下标i表示网络中神经元的标号,即i∈[1,20]；vi和ωi分别表示第i个神经元的膜电位和恢复变量；表示外界输入刺激,i表示均值为0,方差为σ的高斯白噪声；表示神经元之前的耦合项,表示了神经元i受到其他神经元输入的突触电流,具体形式如式(4)所示:

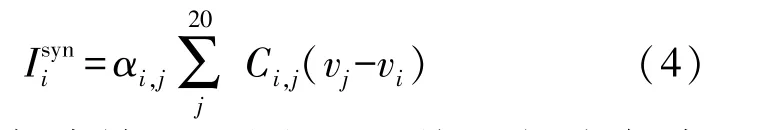
式中:αi,j表示耦合神经元之间的连接强度,与耦合神经元距离成反比；Ci,j是一个神经元之间的连接矩阵,Ci,j＝1表示是神经元之间存在突触连接,Ci,j＝0表示神经元之间不存在突触连接。

将外部刺激施加到小世界网络中的某一FHN神经元上,并改变噪声强度,然后观察网络中各神经元脉冲发放状态,外部刺激信号和噪声的具体信息如式(5)所示

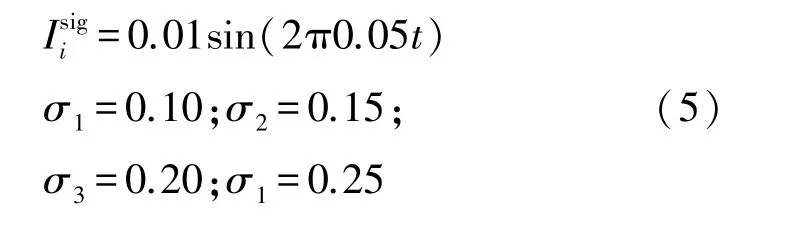
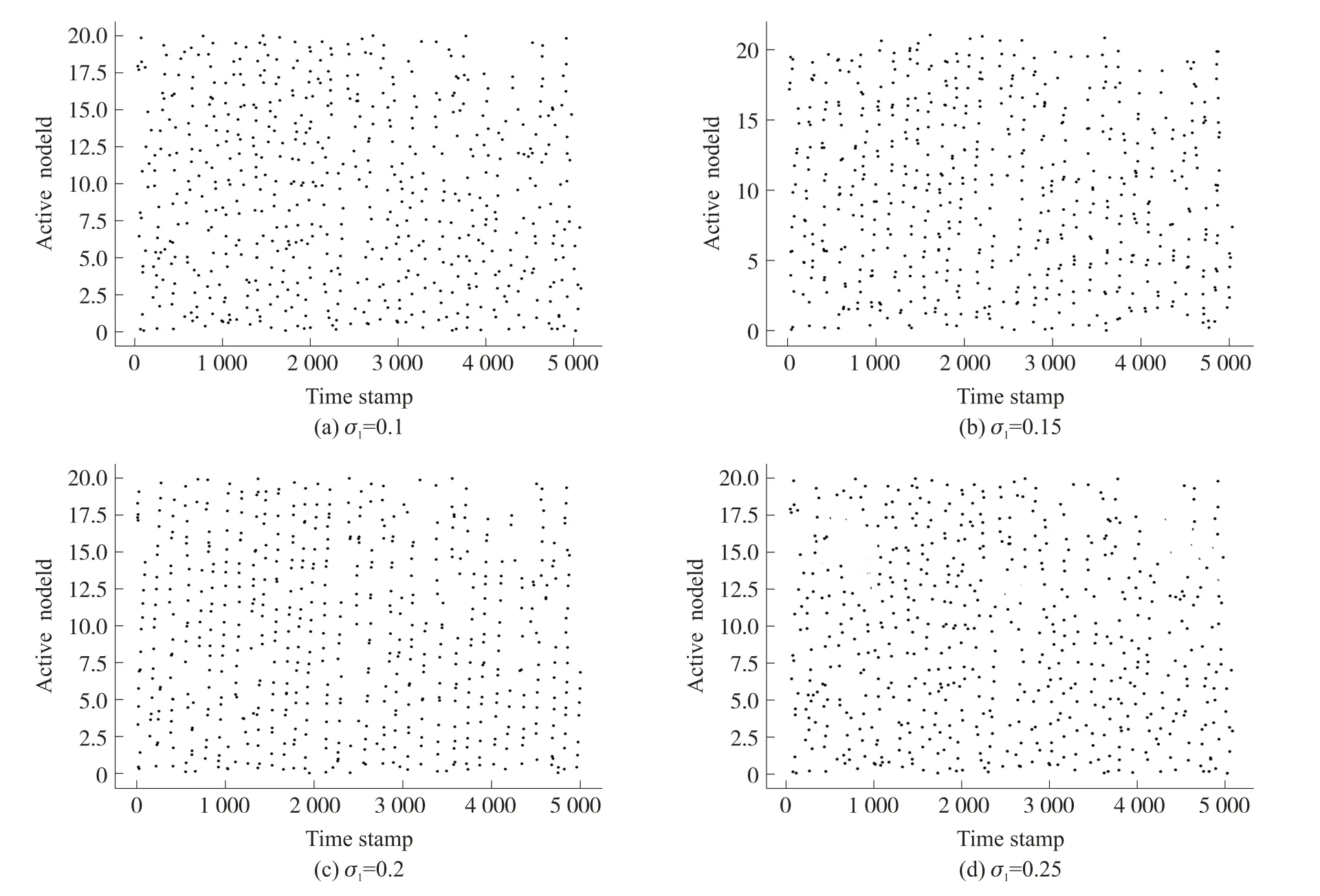
图5 不同噪声强度下神经元脉冲发放示意图

1.3 性能评价指标

目前对随机共振的性能衡量,主要涉及针对周期随机共振的信噪比、信噪比增益和驻留时间分布,以及针对非周期随机共振的相干函数、相关系数及基于信息理论的相关测度指标,为了使评价指标具有更一般性,本文采用基于输入/输出的互相关测度,将归一化后的互相关系数作为性能评价指标,具体形式如下

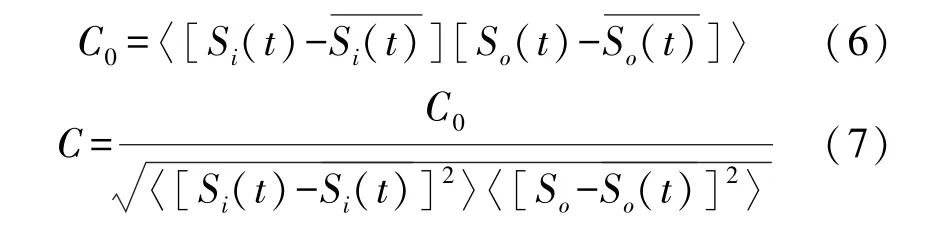
式中:Si(t)表示系统输入信号,表示输入信号均值；So(t)表示系统输出信号,表示输出信号均值；C0表示互相关系数,C表示归一化后的互相关系数。

通过改变小世界网络FHN神经元结点个数,并根据式(7)计算输入信号和输出信号的归一化互相关系数随着噪声强度的变化；可以发现在同等噪声强度下,节点数目的增加在一定程度下可以提高输入信号和输出信号的互相关系数；另外,在节点数目一定的条件下,当噪声强度在一定范围内,互相关系数会逐渐增大,但当噪声强度大于一定值后,输入信号和输出信号的互相关系数会不断降低,这种现象也是非常符合随机共振的特性,具体如图6所示。

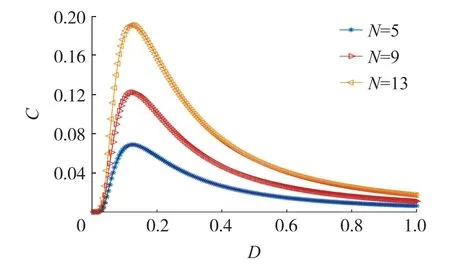
图6 互相关系数变化示意图

为了有效利用小世界网络中各个FHN神经元节点的共振输出,同时为了避免单个节点信息的异常输出,本文实时计算单个神经元节点输入信号与输出信号的互相关系数,互相关系数过低的异常节点输出信息舍弃,基于此提出了一种网络基于互相关系数的均值输出融合策略,具体如式(8)所示。

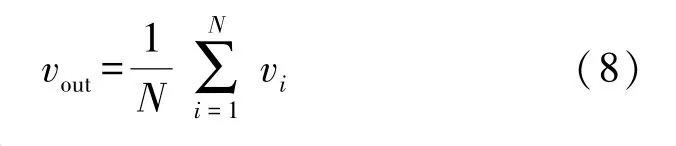
式中:N表示小世界网络中神经元节点的个数。

2 实验结果与分析

为验证本文提出方法的有效性,分别对单频周期信号、多频周期信号、变频非周期信号以及高低电频信号进行了相对应的实验。根据实验条件,小世界网络的实验参数设置为神经元节点数分别为5、9、13,重连概率为0.2,具有连接关系的神经元节点间耦合强度设置为0.01；神经元的参数可设置为εv＝0.01,εω＝1,b＝1。并根据系统参数的不同对实验结果进行定性与定量的分析,为了证实本文方法应用的广泛性和有效性,将常见的信号分为周期信号(其中包含单频周期信号与多频周期信号),和非周期信号(其中包含非周期变频信号和高低电平信号)；对于周期信号,不仅需要对输入信号和输出信号的互相关系数进行分析,同时还需通过频谱分析,以验证随机共振系统是否可以在保证输入信号在噪声干扰下对弱信号增强的前提,并能保证弱信号的主要频率不变；对于非周期信号,由于信号的频率参考意义不大,所以本文主要分析了输入信号与输出信号的归一化互相关系数,以完成整体系统性能的分析。

本文首先进行输入信号幅值为0.5,频率为0.2的正弦弱信号在噪声干扰下的随机共振实验,输入信号的具体形式如式(9)所示。

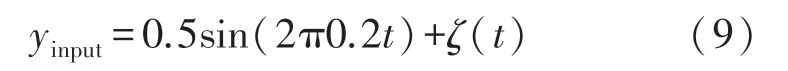
式中:ζ(t)为均值为0,方差为0.1的白噪声。将该信号输入到本文提出的基于FHN神经元小世界网络的随机共振系统,实验结果如图7所示,其中图7(a)为对应的原始信号,从图7(b)中可以发现,由于噪声的作用,原始信号几乎被湮没,而图7(c)输出的实验结果图中可以直观的发现原信号得到了很好的还原,同时信号强度也得到了增强；频率谱图如图7(d)所示,可以看出信号频率也得到了有效的提取。

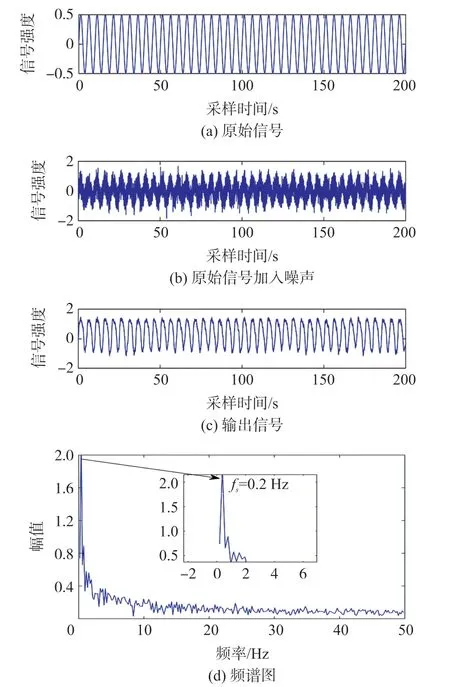
图7 单频周期信号实验结果

为了进一步证明提出的方法对于周期弱信号的有效性,本文使用组合的不同幅值和频率的原始正弦弱信号,并加入一定强度的高斯白噪声,对系统进行测试,其具体形式如式(10)所示。

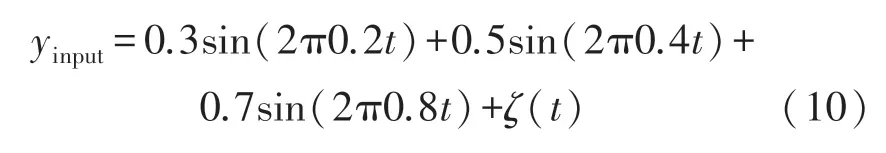
多频周期信号的处理结果如图8所示,从图8(a)原始信号、图8(b)带噪声信号、图8(c)输出信号的实验结果中可以直观的看到,带噪声信号通过小世界网络非线性系统之后,带噪声信号得到较好的还原与增强,使输出信号与原始信号有较强的一致性；同时通过图8(d)的频谱图,可直观的看到三个不同频率的峰值,它们分别是fs＝0.2 Hz,fs＝0.4 Hz,fs＝0.8 Hz,这也与原始信号中存在的三个频率对应,说明本文方法在多频周期信号中仍然有很好的性能。

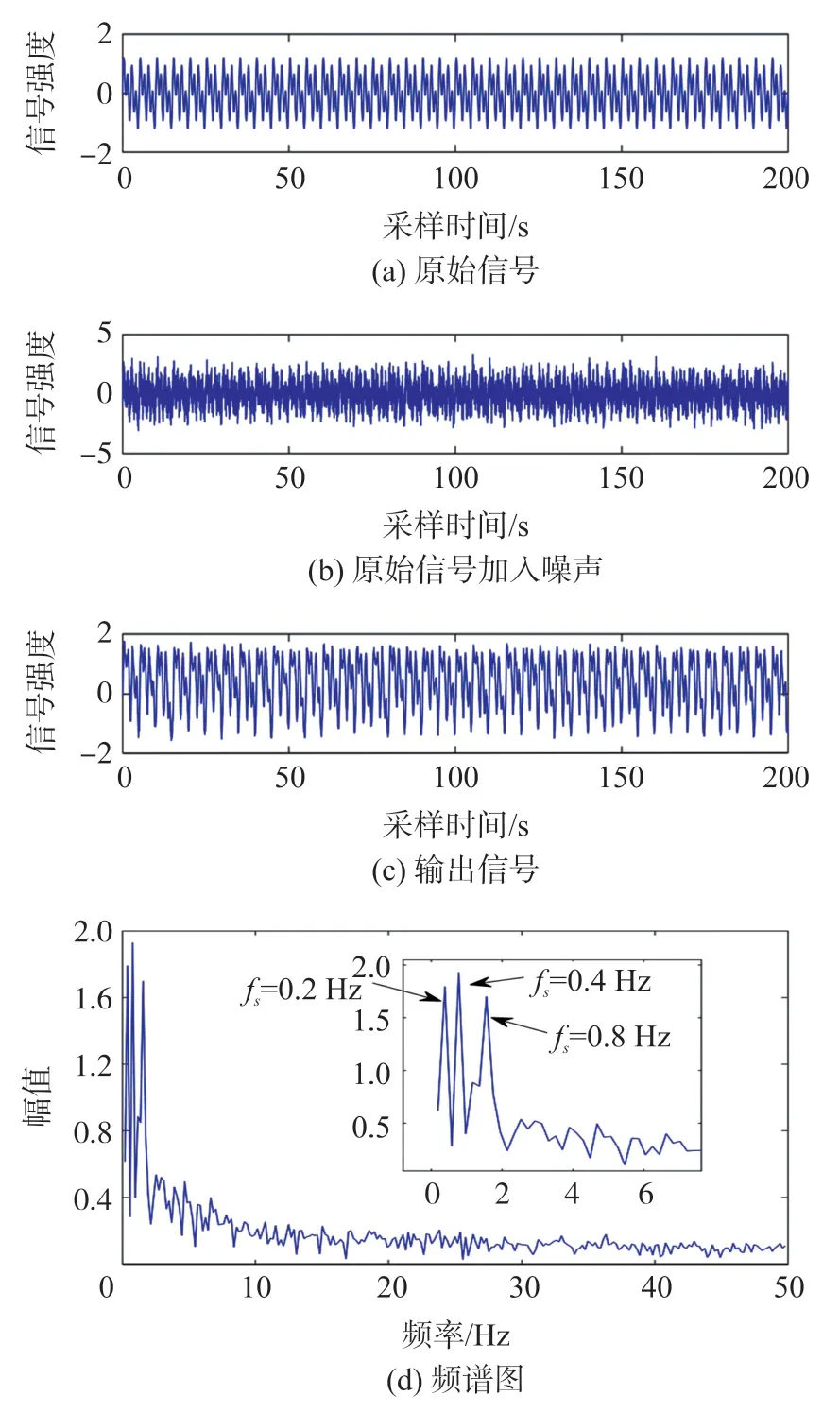
图8 多频周期信号实验结果

另外,由于现实世界的多变性,周期信号只是常见信号的一种类别,各种非周期信号可能更加普遍的存在,而非周期变频信号和高低电平也是现实中较为常见的信号,因此以非周期信号作为实验对象,也更能证明本文方法在弱信号增强还原方面的有效性和实际应用的价值。

其中,非周期变频信号的具体形式如式(11)所示

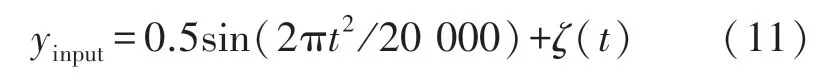
变频非周期信号的处理结果如图9所示,其中输入的原始非周期变频信号形式如图9(a)所示,信号的频率变得越来越高,呈现出一种非线性变化,将其加入强度为0.1的高斯白噪声,其波形图如图9(b)所示,然后将带噪声的信号输入到由FHN神经元构建的小世界网络非线性系统中,然后其输出信号如图9(c)所示,虽然波形仍然有一些噪声干扰,单输入信号的波形依然较好的得到了还原,并且输入信号的信号强度也得到了进一步的增强。同时,我们将小世界网络中的每一个神经元的响应图进行了可视化,如图9(d)所示,每一个神经元都可以在一定程度上对信号进行增强和还原,但相对来说误差会稍微大一些,但经过均值融合之后得到的最终结果会有进一步的提升,这也证明通过对神经元进行集群操作可以更好地提升系统的性能和鲁棒性。

图9 变频非周期信号实验结果

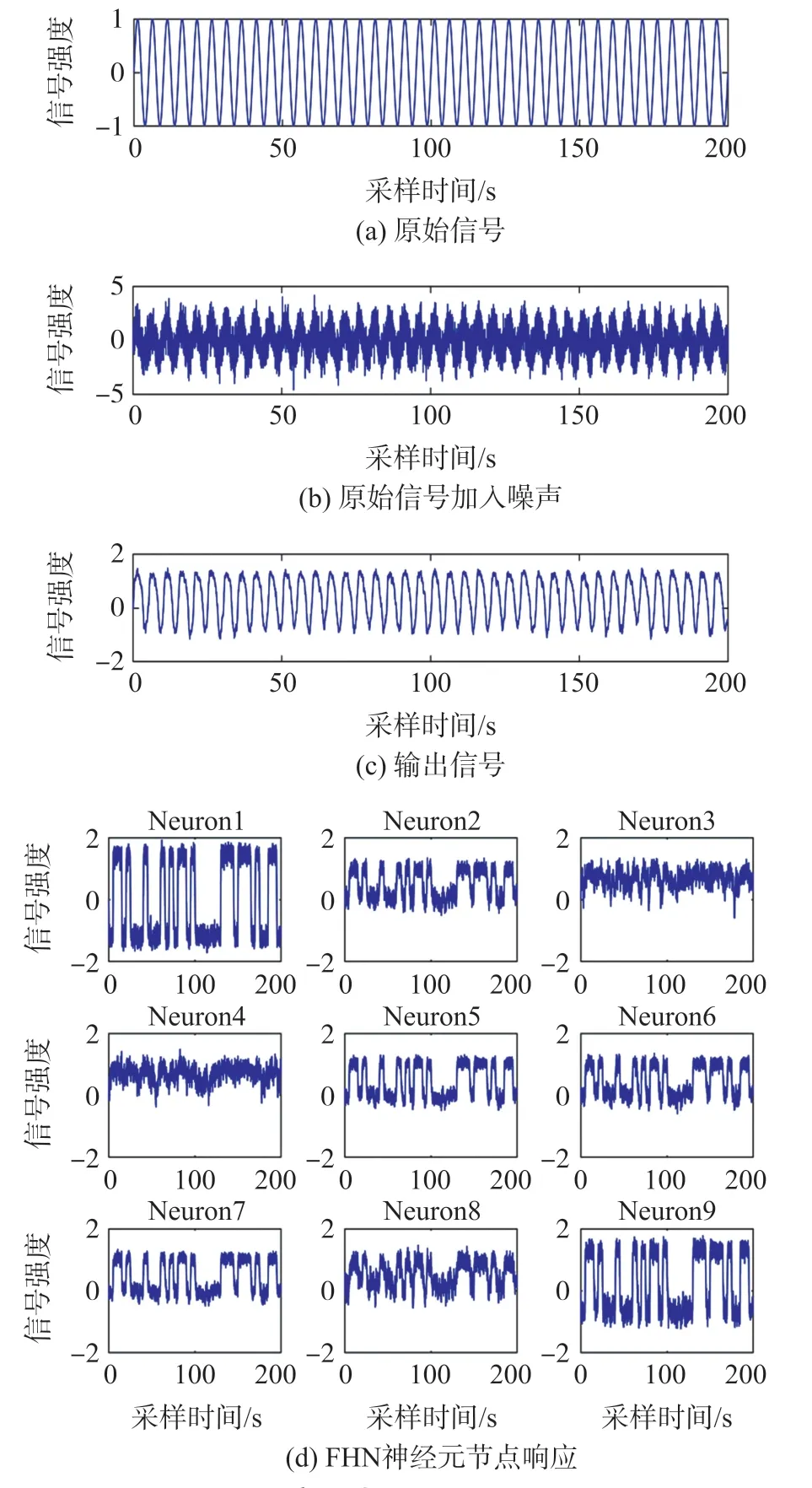
图10 高低电平信号实验结果

最后,考虑到高低平信号在数字电路中具有很广泛的应用,所以如何对电平信号进行噪声的处理具有重要的意义,传统的方法多通过滤波处理,但这同时可能也会导致电平信号的错误处理,因此本文通过小世界网络构建的非线性系统与含噪声的高低微弱电平信号形成随机共振,有效的利用噪声信号的能量,以实现对含噪声弱信号的还原与增强,这能保证电平信号在传输处理过程中即使受到噪声干扰,依然能保持信息传递的准确性,具体实验结果如图10所示,可以发现系统的输出,在噪声的干扰下很好的还原了输入信号的高电平和低电平,并且输入信号的幅值被放大,高电平和低电平的差异也进一步得到了区分。

通过本文提出的小世界网络非线性系统方案与被噪声干扰的弱信号的增强复原方法,实现非线性系统、弱信号、噪声三者的共同作用,达到了很好的随机共振效果,对在噪声干扰下的输入弱信号,较好地实现了弱信号的增强还原。虽然从上述定性的角度,可以发现该方案对周期信号和非周期信号均有较好的实验效果,为了进一步说明方案的有效性,本文从定量的角度,对系统参数做了更加深入的分析,以归一化后的互相关系数作为评价指标,通过调整小世界网络的FHN神经元节点数目,观察系统性能的变化。

根据表1可以得到不同输入信号,在经过不同小世界网络节点数目计算的互相关系数,神经元节点数目越多,互相关系数的值也相应会越大,比如N＝13时,单频周期信号、多频周期信号、非周期变频信号以及高低电平信号的互相关系数值可以分别达到0.987、0.966、0.957、0.961,在三组不同的小世界网络神经元节点数目,结果都倾向于最优；当N＝5和N＝9时,虽然相对于N＝13时性能有所下降,但系统对于弱信号的复原与增强能保持较高的互相关系数,其实验结果也基本与图6的实验现象保持一致,证明了本文方法的有效性。

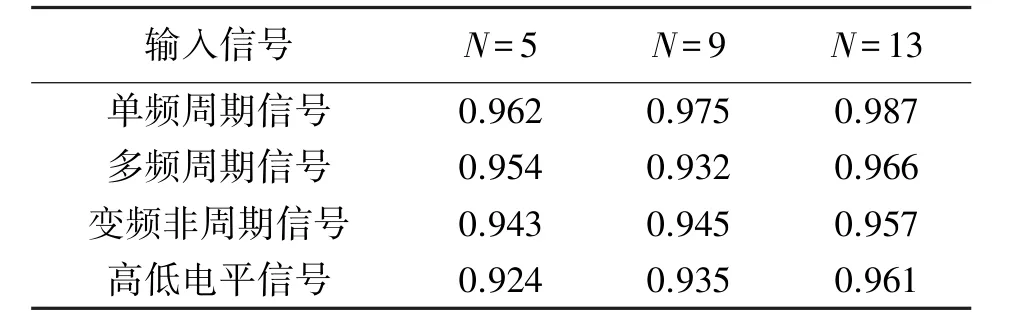
表1 输入与输出信号的互相关系数

3 结论

本文依据生物神经机制,首先研究了FHN神经元非线性系统、弱信号和噪声三者的随机共振特性,其次,受生物神经元网络的启发,构建了以FHN神经元为节点的小世界网络。通过对FHN神经元特性的分析和小世界网络在噪声驱动下的随机共振特点,并分别以周期和非周期带噪声弱信号作为待检测信号,对系统进行了验证,证明了本文提出方法的有效性。随着网络神经元节点数目的增加,在一定程度上可以提高系统输入信号和输出信号的互相关系数,并提高系统的鲁棒性。但网络的最优神经元节点数,将是接下来研究的重点；另外,小世界网络中神经元节点之间的突触连接形式,也有待进一步研究。通过本文的研究,为生物神经网络为什么具有极强的去噪声能力和弱信号检测性能提供了一种新的解释,同时为强鲁棒性的随机共振和实际应用也提供了一个新的思路。