双目结构光系统仿真建模和误差灵敏度分析∗
2021-06-16翟杭军王凌王斌锐高雁凤陈锡爱
翟杭军王 凌王斌锐高雁凤陈锡爱
(中国计量大学机电工程学院,浙江 杭州310018)
结构光系统是获取物体表面三维数据的有效工具,一般由固定机架、数字投影仪和相机组成,易于开发和使用。结构光三维测量系统采集的物体表面点云存在误差,其原因包括相机成像畸变、相机位姿参数(外参)误差、投影仪的投影图像畸变、三维重建算法缺陷等。通过构建和应用误差补偿模型[1-2]可以对上述结构光系统测量误差进行部分补偿。
目前,像素点提取和特征点匹配算法方面已经有较多研究成果,而相机内部结构设计及相机标定等方面还有较大提升空间。Daniel和Gabrie[3]认为许多已有的相机校准技术都使用了简化的模型,忽略了透镜变形,导致成像精度较低,并且提出了一种新的投影图像平面中三维点的图像坐标估计方法,以及基于相机模型描述投影仪成像畸变。崔海华等[4]提出了一种基于六步相移法的伽马射线畸变模型,消除了使用现有投影仪进行条纹投影技术带来的非线性误差。这类针对投影仪投影条纹的优化方法,国内外也有一些学者发表了部分研究成果[5-6]。陈东岳等[7]提出了一种新型全向环形结构光图案,简化了图像特征点的提取,可以快速完成场景定位。达飞鹏等[8]针对条纹投影轮廓术(FPP)系统中存在的局部模糊问题,提出了一种灵活的误差校正方法来处理相机离焦引起的相位误差。关旭等[9]采用了矢量正交归一化目标的双目主动视觉,使得重建后目标轮廓测量的距离误差减少25%,角度误差减少23%。Sert[10]提出了一种具有自动阈值的三步相移标定系统,该标定系统包括相机标定、投影仪标定和深度标定,降低了相机和投影仪镜头的误差。Ye和Zhan[11]提出了一种基于结构光系统的标定参数优化算法,通过最小化标记点之间的距离、夹角和参考平面的平面度等三维测量误差求解最优函数,提高了三维重建精度。然而,这些方法中系统基于误差模型进行了标定并不一定意味着可以完全消除系统误差,实际中可能存在误差补偿错误或补偿后误差放大等情况。因此,有必要对结构光系统进行误差分析和性能评测,从而评估结构光系统误差补偿效果或对其三维测量扫描性能进行评测。
对于结构光系统性能评测或评价方法的研究,近年来也有少数学者发表了研究成果。Bräuer-Burchardt等[12]提出一种基于结构光投影的三维扫描仪性能评测方法,其中扫描标靶是一个金字塔形的截锥,但该方法测试流程的工作量仍然很大。而作为开展3D扫描仪性能评测的国际标准之一,德国VDI/VDE 2634系列标准包含了针对基于区域扫描的光学系统的性能评测标准,规定使用带有两个靶球的球棒来开展3D扫描仪的误差分析和性能评测工作,该球棒尺寸已预先标定,并在测量体积内分别处于至少十个任意的并尽可能均匀的位置采样的特征量包括球棒两端靶球的球心距离(球间距离),用于验证测量系统的长度测量能力,并确保了在标准VDI/VDE 2617中长度测量误差的可追溯性。此外国际标准ISO 10360-13也规定了光学三维坐标测量系统的性能评测验收方法,其中也推荐使用已标定的球棒。
结构光系统的性能评测方法一般涉及的工作量较大,而且经常受硬件上的物理性质影响。如果可以对系统性能评测实验进行仿真分析,那么不仅可以有效降低其性能评测方法设计的工作量,也能够提前发现方法中存在的问题,为系统误差评测分析提供理论基础和开发支持。Liang[13]提出了一种基于单目结构光三维测量仿真系统,并且讨论了部分系统参数对测量结果的影响和参数修正的问题。陈迎春[14]提出一种新的光栅条纹投影轮廓术仿真系统,使仿真系统不再要求投影仪光轴和照相机光轴相交于一点。近年来,也有部分学者通过对结构光系统的仿真解决了一些难题[15-18],如以往的投影仪和相机要求有严格位置关系以及传统的光线追踪法遇到的数值运算问题等。然而,针对双目结构光系统进行仿真分析的研究成果未见报道。
本文在构建基于三步移相法的双目结构光系统数学仿真模型基础上,实现了对靶球的点云重建仿真;然后针对双目结构光系统模型误差对处于不同高度的参考平面时靶球中心位置误差进行灵敏度仿真分析,研究了该试验对靶球处于不同位置时的靶球特征量误差灵敏度,然后分析了现有标准中的结构光系统性能评测方法存在的不足,并提出测试方法改进措施。
1 基于三步移相法的双目结构光系统工作原理和建模
1.1 双目结构光系统坐标系定义
为了分析双目结构光系统测量误差的影响因素,首先对此类系统的坐标系给予定义,如图1所示。
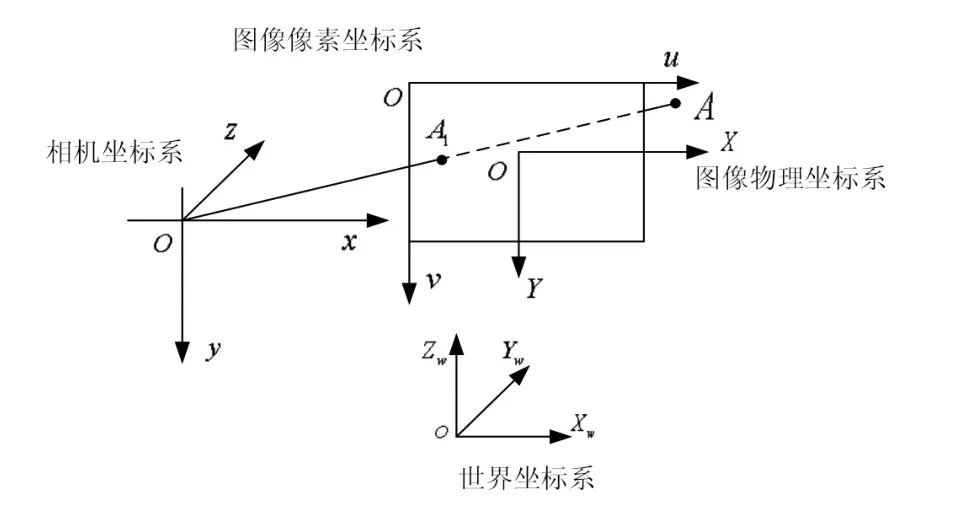
图1 视觉测量系统坐标系定义
图像物理坐标系O-XY:左相机图像物理坐标系为OL-XL YL,右相机图像物理坐标系为OR-XR YR;OL、OR分别为左、右相机的光轴与图像像素坐标系平面中心的交点。
图像像素坐标系O-uv:右相机图像像素坐标系记为OR1-uR vR,uR、vR轴分别与XR、YR平行;同理,左相机图像像素坐标系记为OL1-uL vL,uL、vL轴分别与XL、YL平行,OR在像素坐标系中的坐标为(uR0,vR0)。
相机坐标系O-xyz:以左相机光心O1为原点,光轴为z1轴,建立左相机坐标系为O1-x1y1z1;同理,建立右相机坐标系为O2-x2y2z2。光轴与图像平面垂直,x1、y1分别与图像坐标系的XL、YL轴平行,x2,y2分别与图像坐标系的XR、YR轴平行。
世界坐标系O-Xw Yw Zw:即物体在真实世界中的坐标,是外部的一个固定的参考坐标系,不随着物体的大小以及位置变化,用于描述相机与目标物体的位置关系。
投影仪坐标系P-Xp Yp Zp:在结构光系统中,以投影机的光心P为原点,建立投影仪坐标系PXp Yp Zp,其中所有的y轴方向都垂直纸面向里,如图2所示。
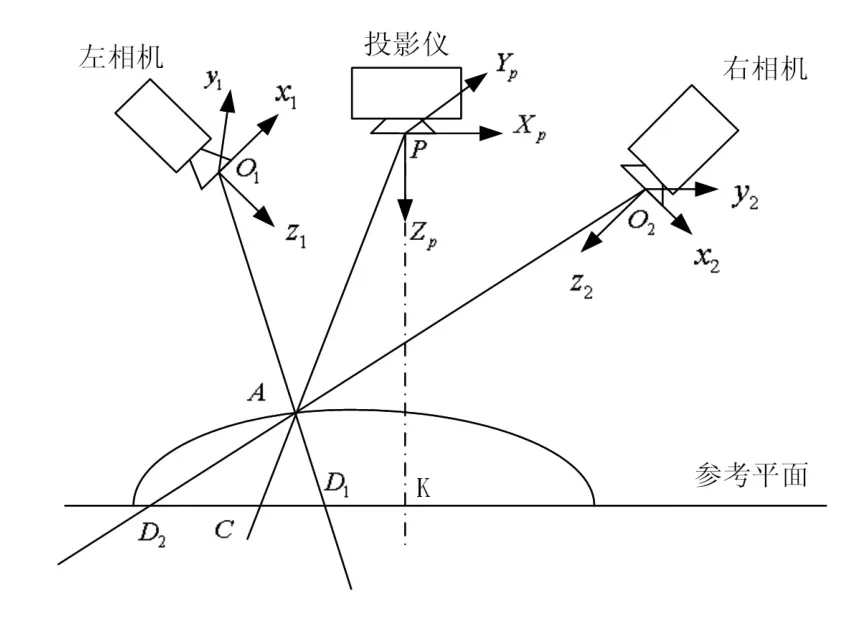
图2 双目结构光系统坐标系之间的几何关系
1.2 相机畸变模型及图像畸变矫正
确定坐标系的定义以及位置关系后可以发现,结构光系统三维扫描中的成像过程的实质上是几个坐标系的转换。首先空间中的一点由世界坐标系转换到相机坐标系,然后再将其投影到图像物理坐标系,最后再将图像物理坐标系上的数据转换到图像像素坐标系。
但是上述得到的相机图像都是受到相机镜头畸变影响的图像。如果要降低图像畸变,,需要对图像进行畸变矫正。相机成像畸变可以分为径向畸变和切向畸变。假定图像像素坐标系OR1-uR vR下的畸变前的坐标为(u,v),经过径向畸变和切向畸变后该坐标在OR1-uR vR坐标系 的(ud,vd)上,即未畸变的图像A1与畸变后的图像A′1之间的关系为:A1(u,v)=A′1(ud,vd)。其中,径向畸变数学模型为:
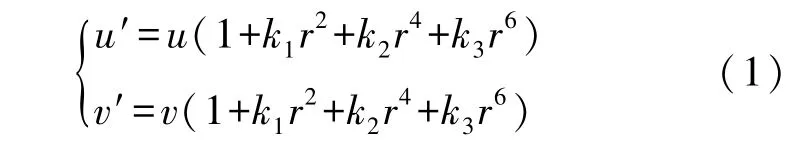
r2=x2+y2,k1,k2,k3为径向畸变系数。
切向畸变数学模型为:
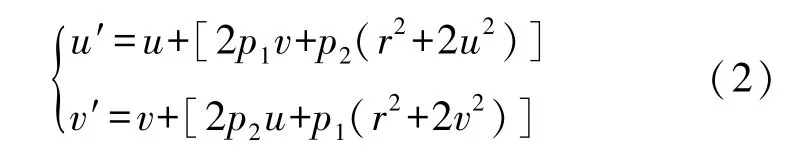
式中:p1,p2为切向畸变系数。
得到相机畸变模型后,即可对图像进行畸变矫正。已知像素值在图像像素坐标系OR1-uR vR中的理想位置坐标:
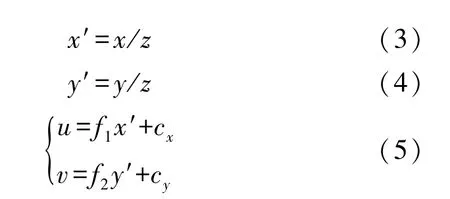
式中:(x,y,z)为相机坐标系下的坐标点,(x′,y′)是归一化之后的坐标。其中,f1,f2,cx,cy分别为左右相机的焦距以及图像物理坐标系的原点相对于光心成像点的纵横偏移量。
像素值在图像像素坐标系OR1-uR vR中的畸变位置坐标:
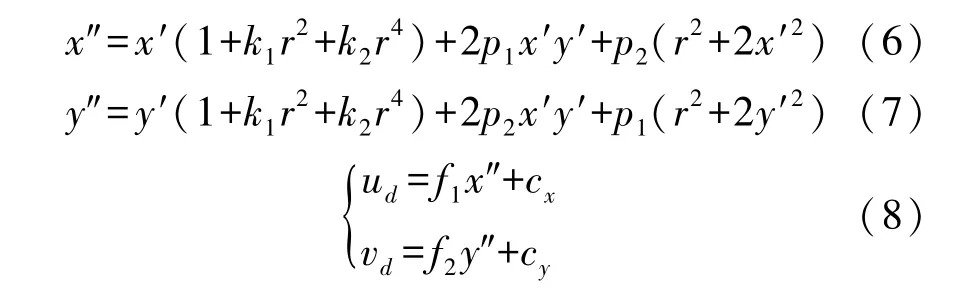
式中:k1,k2为径向畸变系数,p1,p2为切向畸变系数,其中r2=x′2+y′2。因为畸变图像的像素坐标(ud,vd)是已知的,那么未畸变的图像像素坐标(u,v)可以根据式(5)~式(8)求解。
理论上可以通过A1(u,v)=A′1(ud,vd)映射关系可以将他们各个像素坐标点一一对应起来。但是,畸变的像素坐标往往不是整数,所以还需要通过双线性内插法[19]来进行求解。该插值计算以及相机畸变模型准确度问题,都会使得畸变矫正后的图像不可能是完全真实的图像。
1.3 基于三步移相法的结构光技术及解包裹算法
基于相机畸变矫正得到的图像,对其每个像素点坐标进行相位解包裹。基于三步相移法[20]的结构光技术是相移法中测量效率最高的。三步相移法中常用的相位变化量为π/2或2π/3,其中计算公式为:
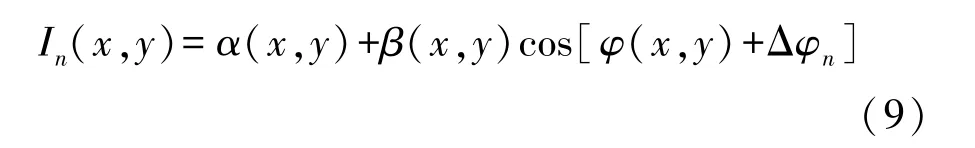
式中:n=1,2,3,采用的相移增量通常是Δφ=2π/3,则Δφ1=-2π/3,Δφ2=0和Δφ3=2π/3,In(x,y)为相位图的灰度值,α(x,y)为环境光强,β(x,y)为条纹光强的调制强度。那么,该方法对应的相位求解表达式分别为[21]:
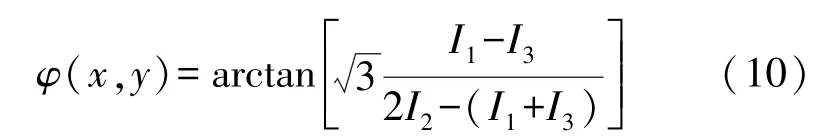
该方法使用反正切法解出的相位在区间(-π,π],只能在该区间内连续,超出该区间就会出现每隔2π的周期会有一个间断点的情况。运用相位解包裹算法可以解决这种问题,该算法在每个2π的间断点上,在相位的邻域判断是否可以加或减一个2π[22]。则相位解包裹算法可表示为:
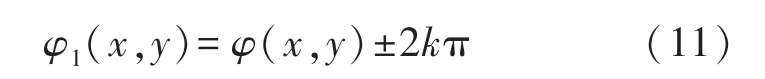
式中:k为整数,φ(x,y)称为包裹相位,而经过相位解包裹之后的φ1(x,y)在区间内是连续且单调。此时,φ1(x,y)称为绝对相位。
1.4 双目结构光测量系统三维重建模型
在得到物体表面的解包裹相位图之后,可以知道图像上每个像素坐标点对应的相位值,然后对其进行左右图像的特征点匹配,即每对匹配点判断像素坐标和相位值是否一致,最后实现物体表面点云的三维重建。
物体表面一点在相机中的成像模型可以简化为针孔成像模型,根据相机畸变模型得到每个图像像素坐标点,再通过图像物理坐标系与图像像素坐标系之间的转化关系,得出每个像素点在图像物理坐标系上的坐标点。假设一个像素物理尺寸的长和宽分别为dx,dy,图像像素坐标系的像素点为(u,v,1)T,对应的图像物理坐标系的点为(xp,yp,1)T,则:
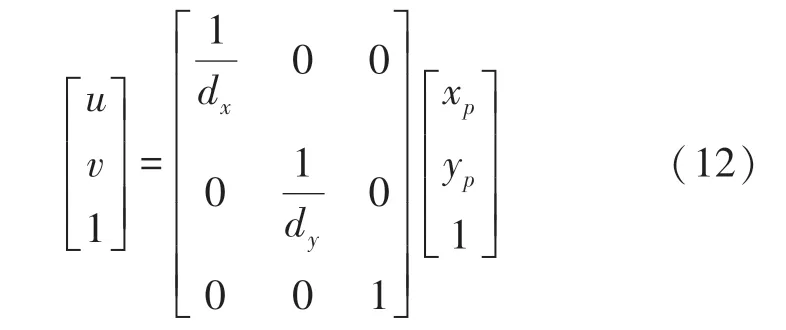
由此,可以根据以上公式推出图像物理坐标系上的坐标值。
双目结构光系统的三维点云坐标计算原理与双目视觉系统类似。图3是双目视觉成像原理图,相机坐标系的原点在相机的光心处,左右相机光心之间的基线距离为b。成像平面距离相机镜头的光心f处,图像物理坐标系的原点在相机光轴与成像平面的交点处,A1(xp1,yp1)和A2(xp2,yp2)分别为点A(x,y,z)在左右图像物理坐标系上的坐标。
图3中,A1到A2的距离为:
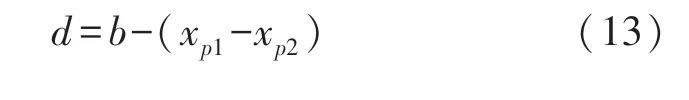
若两相机的图像像素坐标系在同一平面上,则yp1=yp2=yp,根据光学三角法建立线性方程组[23]可得:
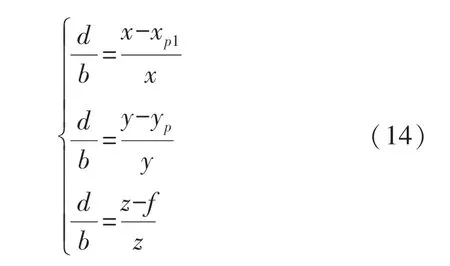
因此,可计算出A(x,y,z)在左相机坐标系下的坐标值:
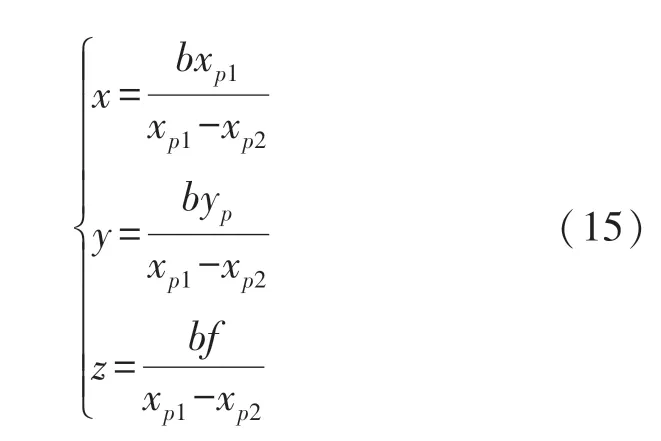
得到该点在相机坐标系上的坐标,最后通过相机坐标系与世界坐标系的旋转平移变换就可以确定实际的三维坐标。旋转矩阵和平移矩阵可以对左右相机进行标定获得。设A点在世界坐标系坐标记为(XW,YW,ZW),再根据针孔成像模型,可以得到世界坐标系和图像像素坐标系之间的转化关系:
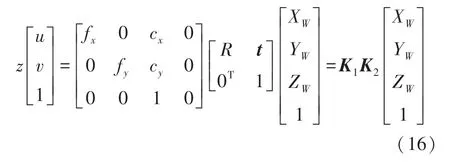
2 基于三步移相法的结构光系统和双目视觉系统的仿真
在由一台相机和一台投影仪组成的结构光系统(SLS)中,实现三维重建必须使用投影仪的模型参数。然而,另外一种常见的结构光系统包含两台相机和一台投影仪,即双目结构光系统。在双目结构光系统中,物体三维重建时可以认为与投影仪模型参数无关。由于其中左右图像的特征点映射是基于三步相移法给出的展开相位完成的,在使用两台相机和一台投影仪的结构光系统中,只有两台相机拍摄的重叠成像区域可以用于重建。
本论文采用基于MATLAB软件平台对双目结构光系统进行仿真,其仿真步骤设计如图4所示,说明如下。
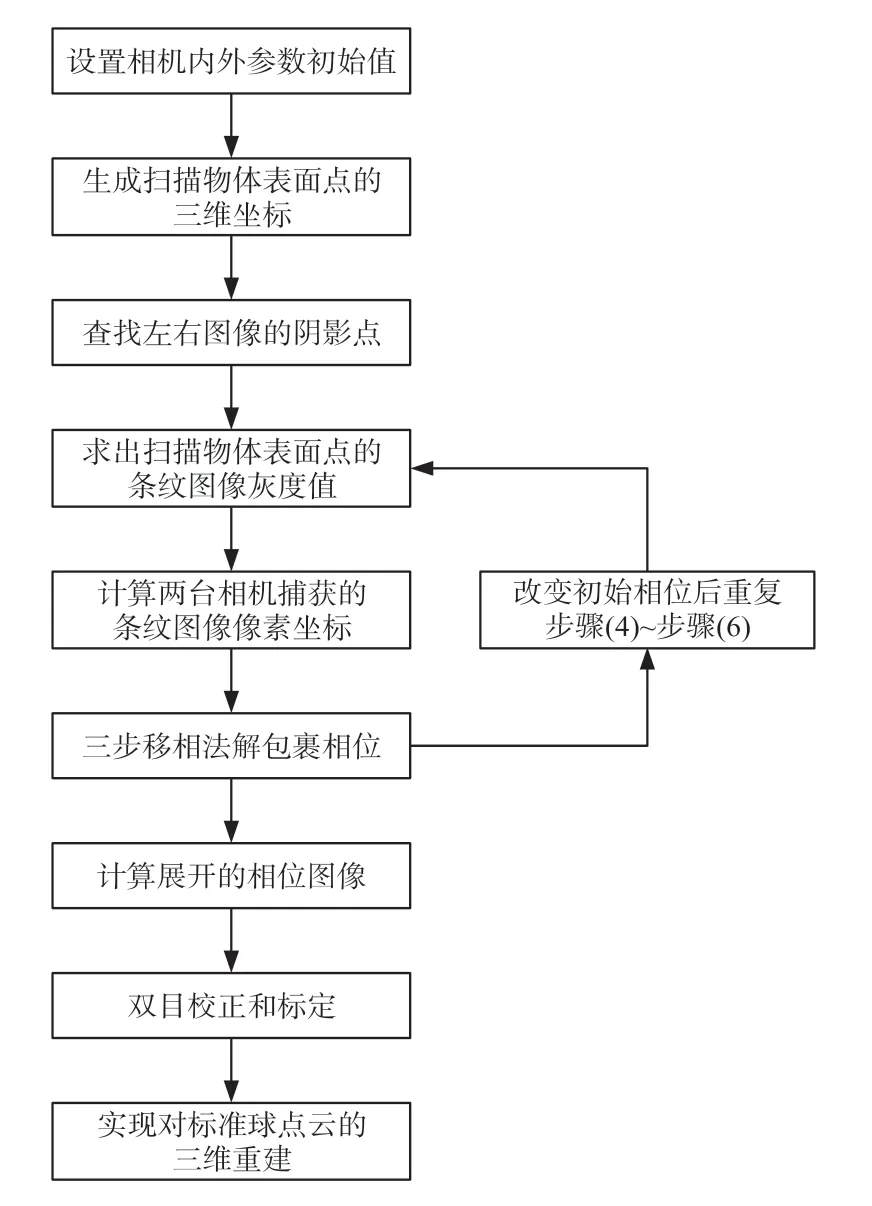
图4 SLS仿真系统流程图
①设置内外参数的初始值:包括理想状态下两个相机的内、外参数以及在相机标定过程中得到的带有误差的左右相机内外参数;此外还包括图像点云的分辨率,结构光系统的初始参数(如结构光的相移值)等。
②生成扫描物体表面点的三维坐标:以相机的坐标系原点为参考点,物体表面的三维点的xyz坐标分别存储在三个经过初始化的矩阵中。参考坐标系原点在相机镜头上,就是相机坐标系作为参考坐标系。默认的坐标数据都是基于这个参考坐标系,而被扫描物体在这个参考坐标系的正下方。该物体是一个平面上的若干个半球组成。这个平面和左相机坐标系的xy轴形成的平面平行。描述被扫描物体需要三个特征量,分别是物体平面所处的纵坐标、各球体中心坐标和球体的半径。
③分别查找左右图像的阴影点:对于物体平面上的点,我们找到球体和光线之间可能的交点的坐标。本文仿真实现中阴影区域的判别分两部分来进行:一是物体表面上阴影区的判别,对于这种物体表面上阴影区域的判断方法用向量法来判断;二是参考平面上阴影区的判别,对于此种情况向量法己经不再适用,本文使用一种迭代搜索法。
④求出扫描物体各表面点的条纹图像灰度值:如图3所示,对应于被扫描物体表面A点,其在左右条纹图像中的灰度值由参考平面上的C点位置和初始相位决定。条纹起点设计在x=xlen/2线上,其中xlen/2是被扫描物体在x轴方向的宽度。
⑤计算两台相机捕获的条纹图像的像素坐标:在上一步得到A点的灰度值后,我们使用两个相机的理想针孔模型和畸变模型,导出左/右条纹图像对应的非整数像素坐标(u′,v′)。(u′,v′)的灰度值即为A点的灰度值。然后,通过基于灰度(u′,v′)的二维插值计算,得到像素坐标为整数的两个相机输出的左右条纹图像灰度。
⑥基于左右图像灰度(u,v)和三步相移方法式(10)计算包裹相位,分别为ΦL1和ΦR1。
⑦改变初始相位后,再重复步骤④~⑥。然后,可以导出与三个初始相位对应的左右相机的所有三个包裹相位图像。图5为某次仿真的包裹相位图像结果。
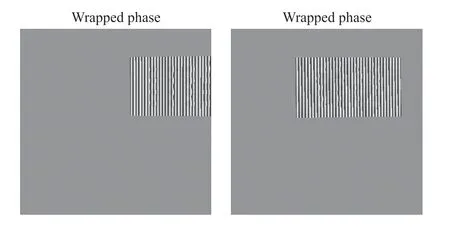
图5 左/右相机包裹相位图
⑧计算解包裹相位:本仿真中基于Goldstein分支切割法,利用步骤⑦的6幅包裹相位图像,计算得到左右解包裹相位图像,其解包裹相位实例如图6所示。
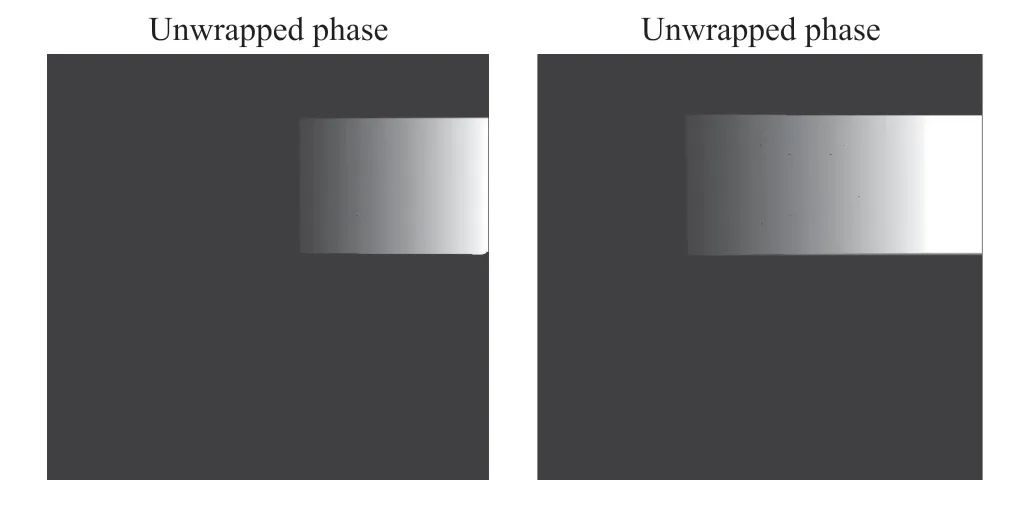
图6 左右相机解包裹相位图像
⑨双目极线校正和标定:对于左右未包裹的相位图像,我们基于已知的旋转/平移矩阵参数和具有误差的相机畸变模型参数来实现极线校正和标定,所使用的极线校正方法是基于立体视觉系统的对极几何的Bouguet算法。因此,可以给出极线校正和标定好的解包裹相位图像。利用极线校正后的左右相机图像,计算得到左右图像匹配点。
⑩重建扫描物体三维点云坐标:基于左右相机的带误差的内、外参数,采用三角法重建扫描物体表面点的三维坐标。某次仿真中靶球重建之后的三维点云图如图7。
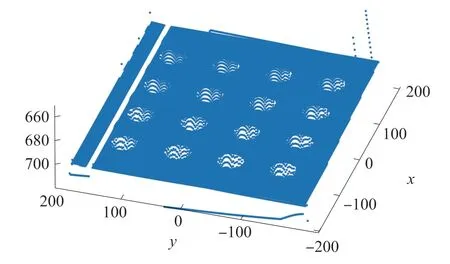
图7 靶球阵列的三维点云仿真重建图
3 双目结构光系统测量误差灵敏度仿真分析
3.1 靶球中心位置对左右相机基线距离的误差灵敏度仿真
根据VDI/VDE 2634系列标准所述,光学三维扫描系统性能评测的方法是测量标靶的某些特征量并且计算误差,测试过程中至少需要改变标靶的十个任意位置,并且这些位置在整个测量空间上的分布尽可能均匀。标准中使用一种球心距已标定的球棒作为标靶。该球棒两端包括直径为50 mm的两个精密氧化铝陶瓷球。通过多次改变该球棒在三维空间中指定的位姿,完成结构光系统的性能评测。但是考虑该标准给出的光学三维扫描系统测试方法中应用到结构光系统时,目前缺乏针对这些测试方法输出对结构光系统模型参数的误差灵敏度分析研究成果,测试有效性缺乏理论分析依据。
在本文双目结构光仿真系统中,通过结构光三维重建原理,对16个靶球进行点云重建。这些靶球半径设置为20 mm,呈4×4排列,两两相邻的球心距为80 mm,在参考平面上呈现的是16个半球体。由于实际中使用带有误差的结构光系统内、外参数进行三维重建,重建的靶球球心与理想中的位置是有偏差的,并且当靶球的平面处于不同高度位置时,测量造成的偏差也可能不同。
表1是结构光系统基线距离误差为+1 mm时,每个放置在不同平面高度位置的靶球进行重建时统计得到的球心位置偏差。从表1中可以看出,在结构光系统对靶球阵列仿真重建中,当只改变z轴的高度,所测量得到的拟合球体中心误差随着参考平面高度的增加而增大,即距离相机越远的靶球的球心位置误差越大。从表1可知,通过改变13次参考平面的高度,得到仿真重建的16×13=208个靶球的球心位置误差,大约分别是4 mm~7 mm左右。由此可见,靶球球心位置误差对双目结构光系统基线距离误差具有较好的误差灵敏度,但是在实际性能测试中并不容易评测得到这个位置误差。
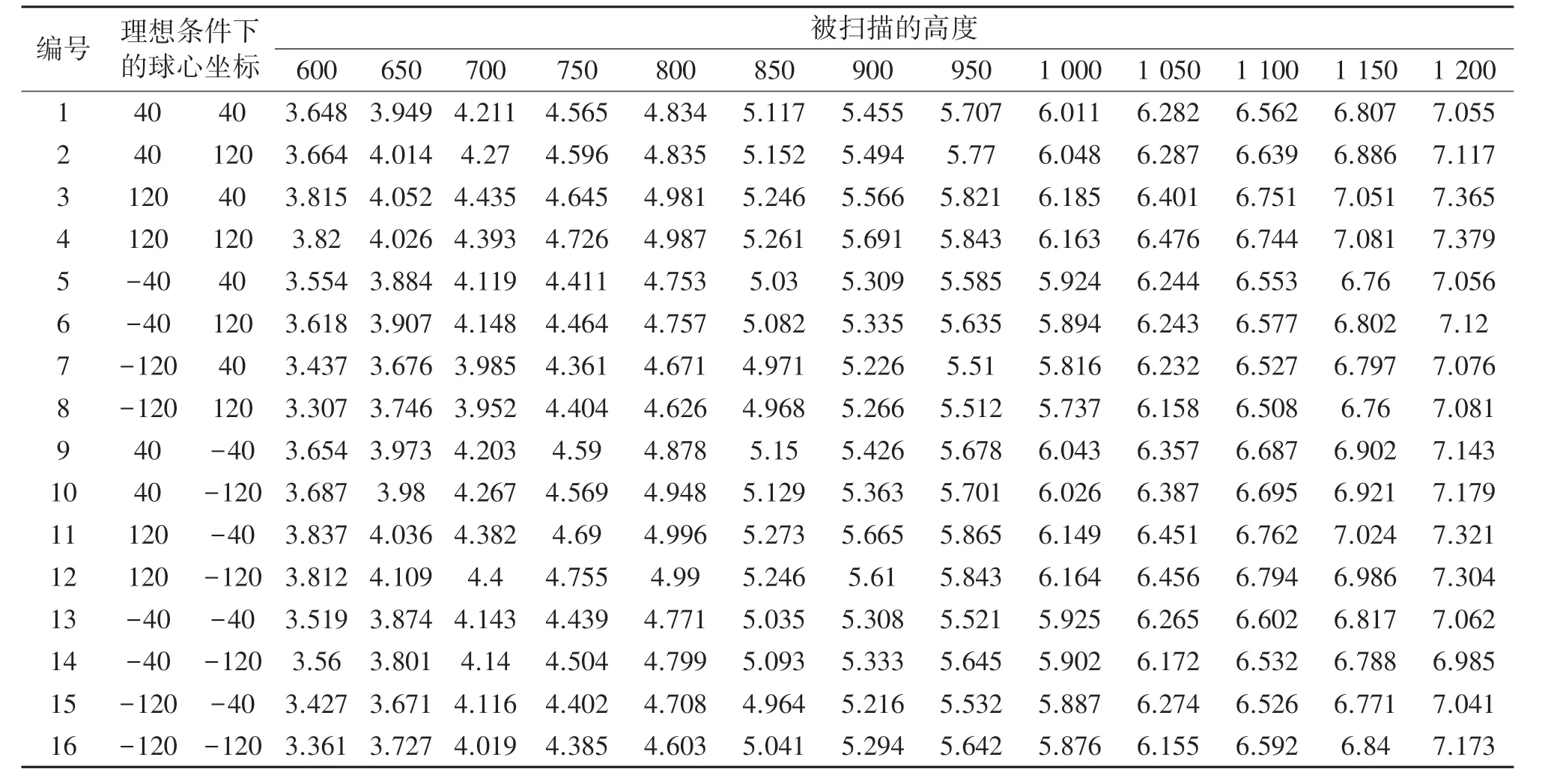
表1 基线距离误差为+1 mm时结构光系统拟合球体中心位置误差
3.2 靶球半径对左右相机基线距离的误差灵敏度仿真
本文讨论的靶球特征量进一步包括靶球的球心距和靶球的半径。首先对靶球的半径进行仿真计算。
表2为结构光系统基线距离误差为+1 mm时,每个放置在不同平面高度位置的靶球进行重建时统计出来的半径误差。通过分析表可以发现,靶球的半径误差对基线距离误差的灵敏度很小。因此,靶球半径对左右相机基线距离的误差并不敏感,如果仅考虑双目结构光系统的基线距离误差,不建议将靶球半径的测量加入到性能测试方法中。
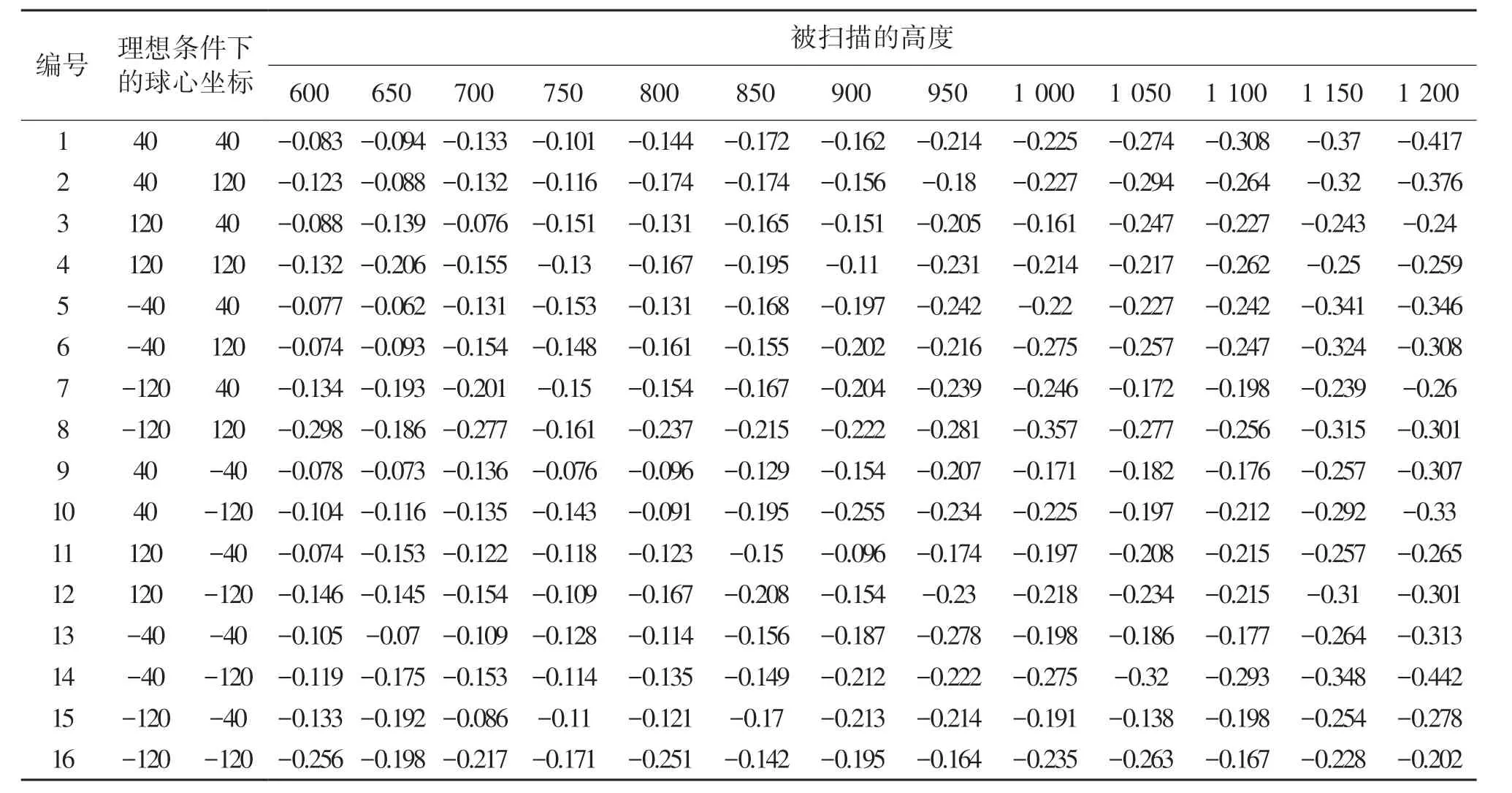
表2 基线距离误差为+1 mm时结构光系统拟合球体的半径误差
3.3 靶球球心距对左右相机基线距离的误差灵敏度仿真
为了优化双目结构光系统性能测试中球棒摆放的位姿,本文仿真实验中进一步分析了靶球两两中心距对左右相机基线距离的误差灵敏度,如图8所示。从图8中得出,当两个靶球的中心坐标位置分别为(-120,-120,600)和(120,120,1200)时,球心距的误差最大,达到约为4.349 mm,即误差灵敏度为4.349。因此,靶球的球心距对左右相机基线距离的误差敏感,球心距可以作为性能测试方法的输出。表中标记为No.1的校准球棒的位姿最适合作为标准测试方法的参考。
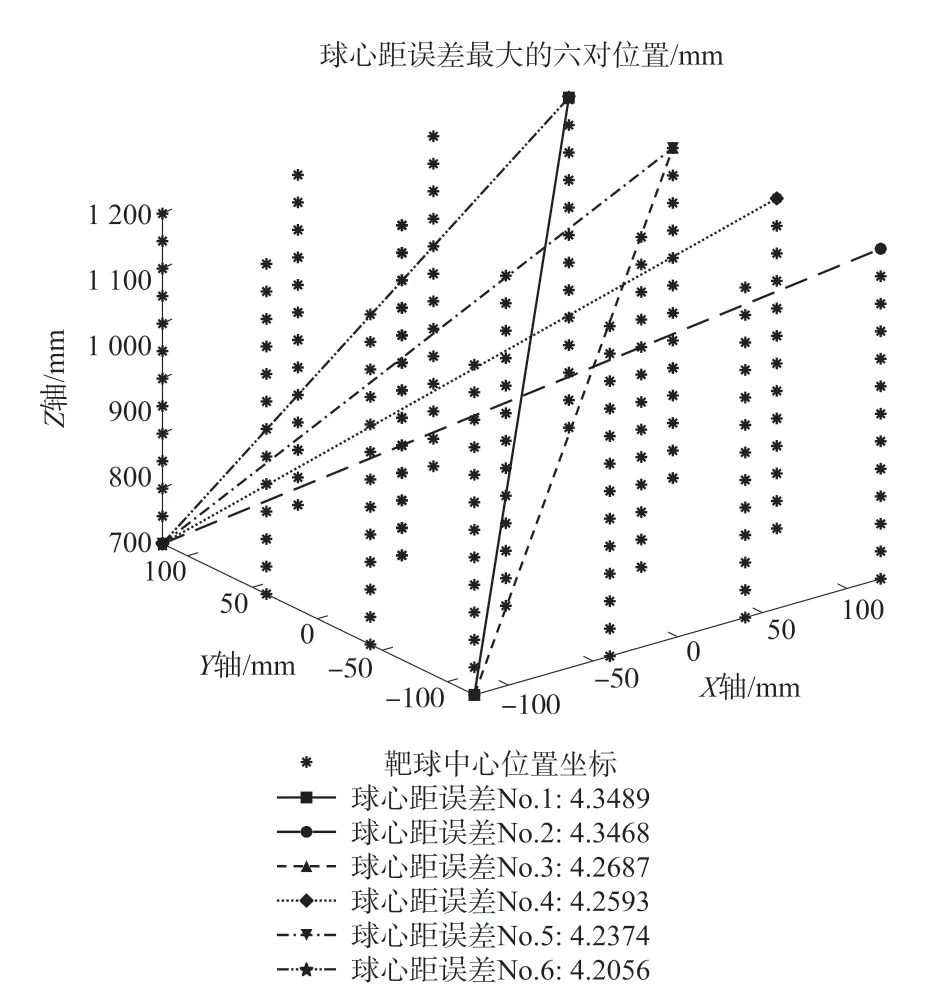
图8 结构光系统的球心距误差分布图
由上述仿真实验可知,球心位置误差和靶球球心距误差都能够较好的反应出双目结构光系统模型的基线距离误差,而靶球半径误差无法有效反应基线距离误差。在仅考虑基线距离误差情况下,靶球球心距对左右相机基线距离的误差灵敏度大小与xyz轴方向呈正相关。
4 结论
由于国内外缺少针对双目结构光系统进行仿真分析的研究,本文构建了一种双目结构光系统的仿真方法。基于仿真实验,完成了球心位置误差、靶球半径误差、靶球球心距误差对于基线距离误差的灵敏度仿真分析。再通过实验仿真得出,球心位置误差和靶球球心距误差两个性能指标能够较好的反应出双目结构光系统模型的基线距离误差,而靶球半径误差无法有效反应基线距离误差。在仅考虑基线距离误差情况下,标准测试方法中的校准球棒放置的位置应该使得两个球在测量范围内x、y、z三个方向的距离尽可能大。而在VDI标准测试方法中,关于校准球棒位姿的确定方法并未给出,本文中校准球棒位姿的确定方法对标准性能评测方法的进一步完善具有较好的理论支撑。但本文仅考虑了左右相机基线距离误差,更多的模型参数的误差灵敏度分析将在后续的工作中开展。
致谢
感谢Bala Muralikrishnan博士和Bingcheng Yang博士对该论文研究工作的热心建议和大力帮助。
