材料性能对双螺杆压缩机转子结构特性的影响
2021-06-16陆正午王军利李庆庆李托雷
陆正午,王军利,2,李庆庆,李托雷,雷 帅,沈 楠
(1.陕西理工大学 机械工程学院,陕西 汉中 723001;2.陕西省工业自动化重点实验室,陕西 汉中 723001)
引言
双螺杆压缩机因噪声和振动小,可靠性高,操作维护方便,适应性强等优点,广泛应用于众多工业部门,并逐步替代其他种类压缩机[1]。螺杆压缩机的核心部件是一对螺杆转子。目前,在研究转子材料的方面,SUH J D[2]提出了采用RTM成型技术使用树脂与增强材料制作螺杆转子,大幅度的减少了螺杆转子重量,其重量仅为传统铝螺杆转子的52%;WEI[3]提出使用CBN磨削工艺对螺杆转子进行精密加工;STOSIC N[4]通过分析刀具磨损率与加工轨迹的规律,提出了加工刀具的设计方法。吴蒙华[5]采用化学镀Ni-P合金工艺使用球墨铸铁(QT600-3)制作螺杆转子,能够有效地提高了螺杆转子的耐腐蚀性能;李宁[6]使用拉伸成型的技术制作螺杆转子,提高了转子的直线度和综合机械性能,尤其是表面硬度与耐磨性;张彦坤等[7]采用成形磨削与砂轮修整技术加工螺杆转子,进一步提高了转子的粗糙度、型线精度等;杨光[8]采用轧制成形的工艺制作阴转子,解决了大螺旋齿形成形和均匀分度难的问题。
上述螺杆转子的工艺与材料研究过程中,忽视了螺杆转子材料性能对螺杆压缩机结构特性的影响,因此,需要研究螺杆转子材料性能对螺杆压缩机结构特性的影响规律。本研究基于CFD/CSD耦合求解技术,研究在双螺杆压缩机内流场热平衡时材料性能对螺杆转子结构特性的影响规律。
1 计算方法
本研究基于单向热固耦合计算方法,采用计算流体动力学软件Fluent,以N-S方程求解流场,流场收敛得到转子表面温度场后,利用GGI(General Grid Interface)插值技术将温度场加载到转子表面结构网格节点上,之后使用Workbench的Static Structural模块求解转子结构平衡方程,稳态分析得到转子的位移场,求得应力分布,具体流程如图1所示。
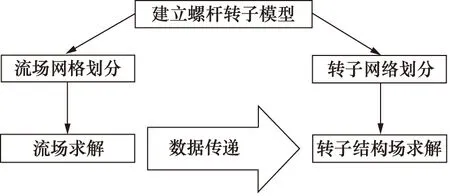
图1 单向热固耦合流程图
1.1 流体求解技术
由于双螺杆压缩机内部流场是一个三维非稳态流场,流场边界会伴随螺杆的转动发生周期性变化,从而引起螺杆压缩机的流场参数在一定范围内产生波动[9]。在压缩机流场达到热平衡时,将其内流场视为准瞬态,对其进行热固耦合数值模拟。计算流体动力学(CFD)的理论基础是质量守恒定律、动量守恒定律、能量守恒定律,其方程如下[10-11]。
(1)
(2)
(3)
式中,ρ为密度;t为时间;v为速度矢量;u,v,w为速度矢量v在x,y,z方向上的分量;p为流体压力;τxx,τxy,τxz等是因分子黏力作用而产生的作用在微元体表面上的黏性应力τ的分量;fx,fy,fz为作用在流体上的质量力;T为温度;k为流体的传热系数;cp为比热容;St为流体内热源及由黏性作用流体机械转化为热能的部分,有时简称St为黏性耗散项。
1.2 结构求解技术
热固耦合计算过程中,结构温度场和热弹性求解的有限元方程[12-13]为:

(4)
DU=GT+F
(5)
式中,M为热容量矩阵[13];T为温度向量;t为时间;K为导热矩阵[13];Q为热流向量;D为刚度矩阵;U为位移向量;G为热应力系数矩阵[13];F为机械力向量。
流固耦合界面上的流体与固体的位移、应力、热流量、温度等相等,满足下列公式[14]:
rf=rs,n·τf=n·τs,qf=qs,Tf=Ts
(6)
上式f为流体;s为固体;r为位移;τ为应力;q为热流量;T为温度。
在单向热固耦合计算模型中,热传导方程的温度分布T受传递热量Q影响,本研究对双螺杆压缩机进行稳态热分析[15],与时间t无关,故温度场式(4)中的温度向量T对时间t偏导项为0,采用有限元单元对方程机械离散,从而获得温度场的单元方程,求解稳态时刻的温度场,接着将温度场代入热弹性方程式(5)中,得到稳态分析的位移场,进一步求得应力分布。
2 验证
为了验证本研究热固耦合计算方法的准确性,以L形大直径掩埋管道为研究对象[16],采用热固耦合计算方法,对温度作用下的热变形进行了计算,管路的几何模型以及内部流域网格模型如图2所示。
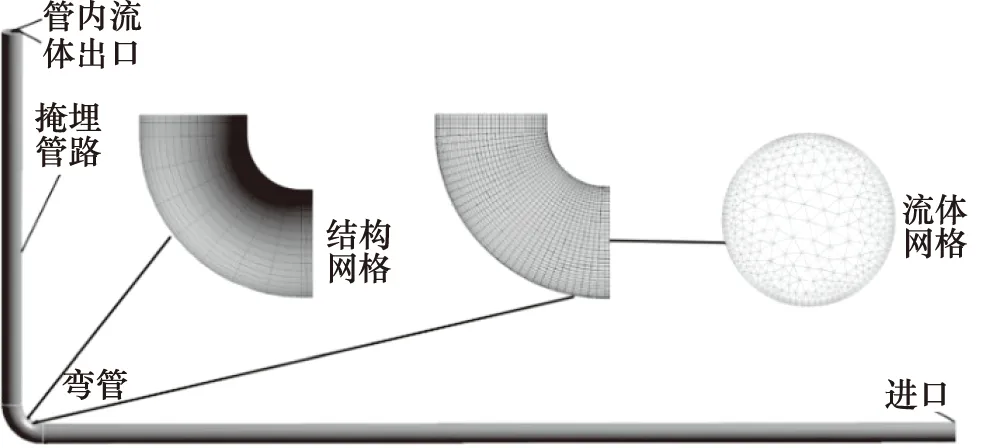
图2 掩埋管路几何模型
计算过程中湍流模型选用标准的k-ε和SIMPLEC求解算法,流体入口设置为压力入口,压力值为1.6 MPa,入口温度为140 ℃,出口设置为质量流出口,固体壁面采用无滑移边界条件。管路内部工作介质为水,管子材料为Q235B,进行热耦合求解时,将管子的出入口设置为无位移约束。
图3是通过计算温度载荷下管路结果云图,温度载荷作用下管路的变形分布情况与文献[12]中温度载荷作用下的变形趋势相同,本研究计算管路的最大变形量为97.354 mm,文献[12]中的管路的最大变形量为97.037 mm,误差在0.3%内。
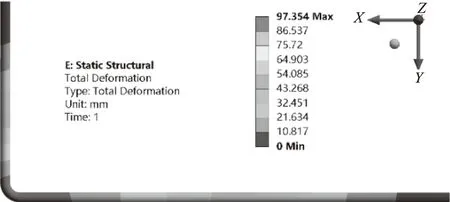
图3 温度载荷下管路变形
数值模拟结果与实验数据进行对比如表1所示,结果表明掩埋管路的流体入口速度、入口压力、入口温度、出口压力以及出口温度的模拟结果与实验中提供的数据误差控制在2%以内。因此本研究采用的热固耦合方法是可靠的,可用于求解压缩机温度场与结构耦合问题。

表1 数值模拟结果与实验数据对比
3 网格划分
本研究的螺杆转子采用的型线为LGY03啮合型线,阳转子齿顶圆直径为115.88 mm,阴转子齿顶圆为92.66 mm,螺旋升角为47.9895°。图4为双螺杆压缩机内流场模型,选择以四面体单元划分压缩机的内部流场与结构模型。网格划分后,压缩机内流场网络节点数513667个,单元数2464345个,如图5a所示。螺杆转子网格节点数796872个,单元数540741个,如图5b所示。

图4 压缩机内流场模型

图5 有限元模型
4 求解设置与结果分析
压缩机吸气口设置为压力进口;排气口设置为压力出口;螺杆转子的壁面条件设置为以绝对速度运动的旋转壁面。控制方程为时均形式的微分方程,采用对旋转流、边界层流及复杂的二相流效果较好的Realizablek-ε湍流模型,采用标准的壁面函数,使用SIMPLEC算法求解,残差控制在10-6数量级以保证收敛。另外,设置环境温度20 ℃,排气压力0.6 MPa,转子轴承位置施加轴承约束,排气孔端的转子轴肩施加位移约束作为固定端,另一端作为自由端。螺杆转子分别选用合金钢(40Cr)、球墨铸铁(QT900-2)、不锈钢(0Cr18Ni9)、钛合金(Ti-6Al-4V)、钛(TA1)进行求解,各螺杆转子材料的性能参数如表2所示。

表2 各螺杆转子材料的性能参数
4.1 温度场求解结果
图6为螺杆转子在3500 rad/min情况下,压缩机内流场阴阳转子壁面温度、热载荷分布云图。从图中可以看出,达到热平衡后,压缩机阴阳转子壁面温度大幅度升高,在靠近排气口处气流压力降低,从而气体膨胀导致靠近排气口处温度下降;阴阳转子热载荷与温度场分布情况相同,最高温度达到96.768 ℃。

图6 转子热分析
4.2 各材料转子热固耦合分析
图7a是排气压力为0.6 MPa、转速为3500 rad/min时,以QT900-2制作的阴阳转子的变形云图。最大变形在阳转子末端,达到0.34402 mm,主要是因为此轴端是动力输入端,工作时需要承受较大扭矩,另外此端是自由端,压缩机转子工作环境温度高,受热膨胀变形。图7b为阴阳转子的应力云图,阴阳转子的啮合区和轴肩位置产生较大应力。

图7 阴阳转子
因为阴阳转子齿顶的变形大小是压缩机工作性能的重要指标,故选择一条螺旋线,沿阴阳转子齿顶各建立螺旋线路径A,B,将齿顶变形投影到路径上,查看沿齿顶变形,如图8所示。
以图8所示的路径A,B由点1到点2的投影路径为x轴,绘制图9,以分析不同材料下阴阳转子齿顶变形随齿顶径向长度变化曲线。由图9a可以看出,阳转子变形随阳转子齿顶径向长度增加而增大,0Cr18Ni9增长最显著,最大变形为0.23023 mm,是TA1的1.918倍。由图9b、图9c可看出,阴转子变形随阴转子齿顶径向长度增加先减小后增大,0Cr18Ni9最大变形0.31989 mm,是TA1的1.91倍。

图8 阴阳转子齿顶变形路径图

图9 阴阳转子齿顶变形
对于阴阳螺杆转子的比较,以图7的QT900-2为例,阳转子最大应力为495.82 MPa,最大变形为0.34402 mm,最大齿顶变形为0.21306 mm;阴转子最大应力为420.05 MPa,最大变形为0.25213 mm,最大齿顶变形为0.2298 mm。阳转子所受应力大于阴转子,而阴转子齿顶变形略大于阳转子。主要原因是阴转子比阳转子的齿顶圆要小,在传动中转动周期要比阳转子要小,导致阴转子的磨损度要比阳转子材料高,因此阳转子材料所用材料应比阴转子材料要软。
表3为各材料螺杆转子的最大变形与应力值,综合图9与表3中可看出,在排气压力为0.6 MPa,转速为3500 rad/min,最高温度达到96.768 ℃的高温环境中,0Cr18Ni9最大应力691.72 MPa,性能最差,远远超过了屈服强度205 MPa,不适合在此工况下选用;40Cr较0Cr18Ni9材料最大变形小,QT900-2次之,Ti-6Al-4V与TA1材料的螺杆转子变形与应力最小,性能最好。Ti-6Al-4V的最大应力远远低于屈服强度970 MPa,安全系数较高;40Cr与TA1的最大应力稍低于屈服强度,安全系数较小。

表3 各材料螺杆转子的最大变形与应力
4.3 研究弹性模量与热膨胀系数对转子变形影响
为研究在双螺杆压缩机内流场热平衡时材料性能对螺杆转子结构特性的影响规律。设计虚构材料性能试验,以分析转子变形与弹性模量和热膨胀系数的关系,以40Cr、QT900-2、0Cr18Ni9、Ti-6Al-4V、TA1的平均泊松比:0.3028、平均质量密度: 6379 kg/m3为虚构材料的泊松比与质量密度,参考上述5种材料性能,在[1.10e-05,1.66e-05]以8e-07为间隔取8个数为热膨胀系数,在[1.27e+11,2.11e+11]以1.2e+10为间隔取8个数为弹性模量,设为虚构材料性能参数。
由表4、表5可以看出阳转子最大变形与热膨胀系数为近似线性正相关,与弹性模量为近似线性负相关,故使用MATLAB进行多项式拟合得到阳转子最大变形公式(7)与阴转子最大变形公式(8):

表4 虚构材料的阳转子最大变形 mm

表5 虚构材料的阴转子最大变形 mm
μ=0.003845-3.221e-15*E+3.169e+04*α
(7)
μ=-0.0001544 -4.346e-15*E+ 2.347e+
04*α
(8)
由式(7)、式(8)作出拟合效果图10,由图10可看出数据点都近似在拟合面上,拟合效果很好,在MATLAB中计算得到式(7)数据拟合的和方差为1.488e-06、均方根为0.0001562;式(8)数据拟合的和方差为4.846e-06、均方根为0.0002818,都接近为0,符合数据拟合要求。
由式(7)、式(8)和图10可知阴阳转子最大变形与弹性模量的相关性很小,主要与热膨胀系数相关。代入40Cr、QT900-2、0Cr18Ni9、Ti-6Al-4V、TA1的弹性模量与热膨胀系数到式(7)、式(8)与4.2节实验结果对比,检验公式精准度。

图10 公式拟合效果图
从表6~表8可知式(7)、式(8)误差和与平均泊松比的偏差正相关,主要误差由泊松比与虚构材料的泊松比的偏差导致,公式计算误差在3%以内,精确度高,可用于估算阴阳转子最大变形,为转子结构设计提供了一定的理论依据。

表6 公式(7)精准度检验

表7 公式(8)精准度检验
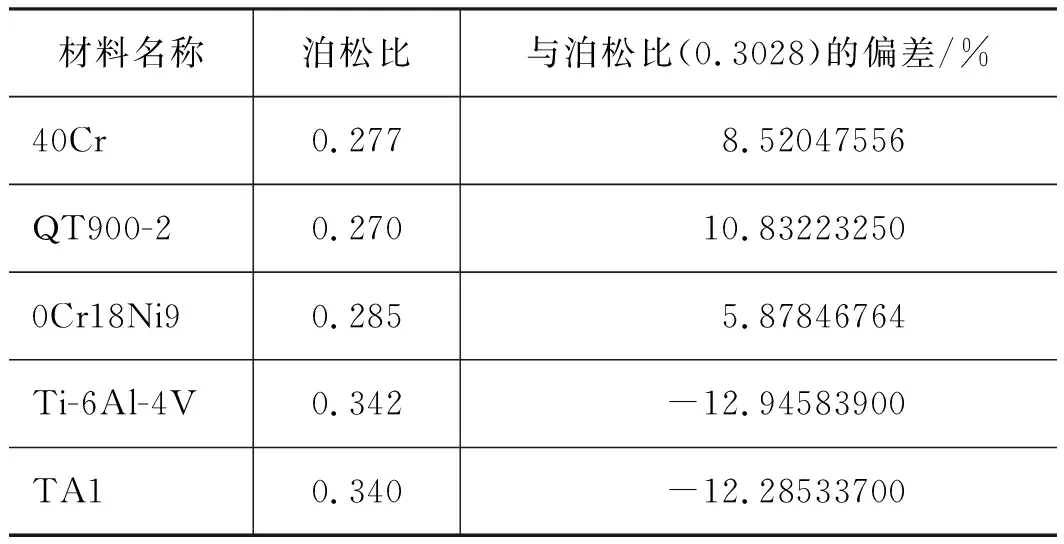
表8 各材料泊松比偏差
5 结论
本研究基于CFD/CSD热固耦合方法,模拟了不同材料的螺杆转子在高温环境下的工作情况,通过求解N-S方程与结构运动方程,得到了双螺杆压缩机在排气压力为0.6 MPa、转速为3500 rad/min下的螺杆转子壁面温度场,并加载到各材料螺杆转子上得到其应力和变形,得到以下结论:
(1) 在高温环境下,螺杆压缩机的转子应选择Ti-6Al-4V 作为首选材料,不宜选用0Cr18Ni9材料;
(2) 相同材料的阴阳转子,阴转子的最大应力与变形小于阳转子,齿顶最大变形略大于阳转子,因此阳转子材料所用材料应比阴转子材料要软;
(3) 在高温工作环境下螺杆转子的变形主要和热膨胀系数线性正相关,与弹性模量线性负相关较小,受泊松比影响很小,在此工况应主要考虑材料的热膨胀系数。
