基于时间特征分割和降维谱聚类的液压系统内泄漏故障诊断
2021-06-16黄亦翔刘成良
张 轩,张 旭,黄亦翔,刘成良
(上海交通大学 机械与动力工程学院,上海 200240)
引言
液压系统在各类工程机械、飞机、机床等行业有着广泛的应用。内泄漏是液压系统最常见的故障之一,它的发生会导致系统压力不足,工作不平稳,内泄漏可能发生在液压泵、液压缸、换向阀等多个位置,通过对缸内流量或压力进行监测,往往可以观察到泄漏的发生[1],但只凭借经验观察很难判断泄漏量的大小。对液压系统的故障诊断往往是先从压力信号中提取特征,再通过支持向量机、特征距离或状态空间的方法对信号进行分类,从而完成故障诊断[2-4],近些年来使用深度学习的方法进行故障诊断的案例也越来越多[5-6],然而这些监督学习的方法往往需要大量规范的样本进行训练,在数据量不足时往往很难发挥作用,而液压内泄漏数据往往也很难大量提取。无监督学习不需要大量的样本来训练模型参数,往往可以发现数据的内在联系,对界限不明显的数据往往也有着较好的效果,常用于故障诊断的无监督学习方法有K均值聚类、密度聚类、谱聚类等[7-8]。
谱聚类作为最有效的无监督学习方法之一,在故障诊断领域也有诸多的应用,宋天祥等[9]利用声信号进行谱聚类对托辊的故障进行分析;刘建峰等[10]基于继电保护信息和改进谱聚类分析对电网故障区域进行了识别。然而液压系统压力并不是稳定信号,随着活塞的运动在不同阶段特征也有所不同,直接提取特征进行谱聚类会造成很大的不稳定性,本研究提出了一种基于时间特征分割信号构建特征,然后在降维后进行谱聚类的故障诊断方法,采用小波分析的方式提取液压缸进口压力信号中的平稳段,再提取平稳段信号的时域和频域特征,通过PCA对特征进行降维处理后使用谱聚类的方式进行故障诊断,与K均值聚类和其他几类聚类方法对比显示该方法有着较好的效果。
1 液压内泄漏故障诊断原理
液压内泄漏故障诊断流程如图1所示,首先在时域上对压力数据进行特征片段分割,提取其中的高压稳定片段,然后在该片段上提取时域和频域特征,接着对这些特征使用主成分分析的方法提取特征的主要信息,最后使用谱聚类进行分层故障诊断。

图1 液压内泄漏故障诊断流程
1.1 时间特征分割
液压缸进口压力是一个时变信号,其特征随着液压系统的变化而改变,在时域上可以分为压力上升、高压平稳、压力下降和低压平稳四个阶段。四个阶段的压力信号特征有着明显的区别,其高压平稳段数据量最多,分析特征时误差更小,因此需要对信号的高压平稳段进行提取。信号每个阶段之间的不连续性可以看作是第一类间断点,因此它是分割不同阶段的一个具体指标。
间断点检测在故障诊断、状态监测等领域有着广泛的应用[11-12],主要方法包括极大似然估计法、核函数法、傅里叶变换法、小波分析法等[13]。小波分析是处理非平稳、非线性信号的有力工具,在时间序列变化点检测中具有良好的效果,它的时间窗在低频时自动变宽,在高频时自动变窄,可以有效分析信号的瞬变现象。因此将小波分析的方法应用于液压缸进口压力信号的时域分割,小波变化的定义如下:
若ψ(t)是一个平方可积函数,且其傅里叶变换ψ(w) 满足条件:
(1)
则其称为小波基函数,可按下式变换得到小波基函数:
(2)
式中,a为伸缩因子(尺度参数);b为平移因子(位置参数)。
则使用上式定义的连续小波对信号f的连续小波变换定义如下:
(3)
Daubechies小波是一类具有有限消失矩的紧支撑的正交小波,随着其阶次的增大消失矩也会越大,Daubechies小波是不对称的,除了db1小波外没有显式表达,对不同波形进行小波分析效果也不同,需根据实际情况进行选择,对高压低压变化明显的液压信号而言,选择如图2所示的模拟信号进行实验,实验表明db4小波在间断点检测上效果最为明显,适合于液压信号时间特征分割。

图2 db4小波检测间断点
1.2 特征提取降维
对分割后的平稳段压力信号可以进行有效的特征提取,主要提取的是时域特征和小波域特征。考虑到特征的维度比较大,不同特征间包含的信息有所重叠,且部分特征包含的非敏感信息可能会造成故障诊断时的误差,因此需要对特征进行降维处理,保留其主要信息以利于后续的故障判别。特征降维的主要方法有主成分分析(PCA)和流形学习,后者主要包括拉普拉斯映射(LE)、局部线性嵌入(LLE)等。流形学习主要用于非线性维度的降维,经实验液压内泄漏数据在线性降维条件下表现更佳,因此采用主成分分析的方法。
主成分分析是具有最近重构性与最大可分性的一种降维方法,降维后的低维向量不会损失样本特征间的差异性,并且可以通过一个可以由直线推广到高维的超平面对所有样本进行恰当的表达。降维后,数据样本的投影空间应该满足样本点到投影平面距离足够近,样本点到投影平面的投影能尽可能分开。该算法具体过程为:
(2) 样本数据xi在低维空间坐标系的投影zi={zi1,zi2,…,zim},满足:
(4)
其中zij是xi在低维坐标系下第j维的坐标。
(3) 根据最近重构性,为了保证投影后样本点的方差最大化,原样本点基于重构样本点之间的距离满足:
maxWtr(WTXXTW)
(5)
s.t.WTW=I
式中,WTXXTW为样本方差;I为单位矩阵。
(4) 对式(5)使用拉格朗日乘子可得:
XXTW=γW
(6)
对协方差矩阵XXT求取所有特征值,设降维后的维数为m,将所得的特征值按照降序排序表示为:γ1≥γ2≥…≥γm,则前m个特征值对应的特征向量即为主成分分析所求的解,如式(7)所示:
W*=(w1,w2,w3,…,wm)
(7)
主成分分析的降维方法增强了数据的主要信息,更好的体现其本质特征,并剔除了一些次要信息以及可能由噪声产生的特征,使后续的诊断过程更容易进行。
1.3 谱聚类诊断方法
谱聚类是一种基于图的聚类方法,与传统的K均值聚类等方法相比,它不受到样本簇形状的影响,对于各类型样本均可以达到全局收敛的效果。谱聚类将所有的数据看作空间中的点,各个点之间用权重不同的边相连,两点距离越远边的权重越低。聚类时通过对所有数据点组成的图进行切图,使得切图后各个子图内边的权重和尽可能高而图之间的权重和尽可能低,从而达到聚类目的。其主要流程如下:
(1) 根据样本集下X=(x1,…,xn),建立相似矩阵S,其中Si, j表示xi,xj向量间的距离。
(2) 根据相似矩阵S构建邻接矩阵W和度矩阵D,然后计算得到拉普拉斯矩阵L=D-W。其中邻接矩阵W一般采用径向基函数(RBF)构建:
(8)
度矩阵D为邻接矩阵之和,是一个对角矩阵。
(9)
(3) 构建标准化后的拉普拉斯矩阵D-1/2LD-1/2并计算其最小的m个特征值对应的特征向量f。
(4) 将f组成的特征向量按行标准化,组成新样本集F,F中的每一行为一个新样本,通过K均值聚类的方式聚为n类。
(5) 根据聚类结果得到最终切图方式,得到结果C。
2 实例验证
本研究进行了液压系统内泄漏的模拟实验,对液压缸泄漏、液压泵泄漏和换向阀泄漏三种情况进行了模拟,通过阻尼孔的方法实现对液压泵和液压缸泄漏的模拟,通过模拟阀芯的磨损实现对换向阀泄漏的模拟,并通过磨损量的大小分别模拟严重泄漏、中等泄漏和轻微泄漏,并在液压系统多个位置安装了压力传感器,实验台示意图如图3所示。
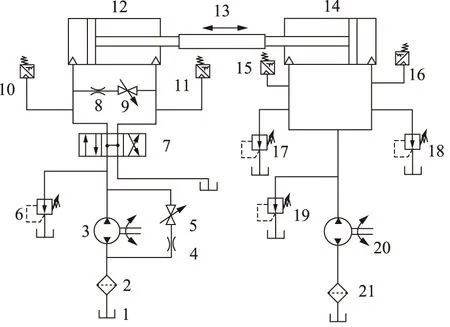
1.油箱 2、21.过滤器 3、20.液压泵 7.手动换向阀4、8.阻尼孔 5、9.截止阀 6、17~19.安全阀10、11、15、16.压力传感器 12.实验油缸13.接头 14.加载油缸图3 实验装置示意图
选择液压缸入口压力信号作为特征信号,每段信号采集时液压缸活塞来回运动2~3次,共采集得到60段信号,液压缸、液压泵和控制阀内泄漏工况下各20段,且每种工况下泄漏量大小均为从小到大均匀覆盖,采集到的信号如图4所示。

图4 不同位置内泄漏得到的入口压力信号
可以看到每个压力信号均由不同的阶段组成,为保证特征的一致性,在进行特征提取之前,需要对高压平稳段信号进行提取。如图5所示,采用db4小波寻找间断点,对间断点之间的片段进行分割提取,只保留其中的高压平稳部分。

图5 小波分析提取时域片段
对提取出来的信号,提取其时域特征和小波特征,如表1所示,时域特征主要包括平均值、均方差、峭度因子、裕度因子等,小波特征为4阶Symlets小波包的5层分解子频带能量特征。

表1 主要时域特征
从信号中提取的时域和小波特征包含丰富的原信号信息,但不同特征代表的信息有部分重叠,一些信号也带有非敏感特征,对无监督学习有很大的影响。此外,谱聚类作为一种图聚类方法,聚类过程较为复杂,当数据维度较大时耗时也会急剧增加。因此需要对高维度的数据进行一定的约束,消除非敏感特征对诊断效果的影响。最终通过主成分分析的方式将12维度特征降至5维,保留了其中的关键信息。
对降维后的特征进行谱聚类故障诊断,类别为3类,采用高斯核函数建立相似矩阵,对液压泵、液压缸和换向阀的数据分布进行聚类诊断,每类数据分为高、中、低3种泄漏类型,每个类型均包含3组已知类别数据作为标签参与聚类,最终得到的结果如表2所示。

表2 降维谱聚类测试结果
从表2中可以看到,对于不同位置的液压泄漏,使用谱聚类的方法均有不错的效果,在液压泵和液压缸上的准确率均达到100%,在对换向阀泄漏的诊断中,有一例轻度泄漏数据和一例重度泄漏案例被诊断为中度泄漏。两例轻度泄漏的案例被诊断为重度泄漏,总准确率为93.33%,可以认为诊断基本准确无过大偏差。
3 结果对比
本研究分别从几个角度进行了对比,首先是对比采取不同的降维方式与不降维情况下谱聚类诊断的准确率;其次是对比不同聚类诊断方法的准确率,分别在液压缸、液压泵和换向阀3类元器件上进行实验统计准确率,其中AP聚类和DBSCAN聚类结果均近似随即值,可以认为不适合液压内泄漏数据簇,其余模型对比如表3所示。

表3 模型对比
通过与LLE降维谱聚类和直接谱聚类的结果对比发现,对特征数据直接进行谱聚类诊断已经可以取得较高的准确率,在使用PCA方法降维后可以进一步提升其准确率,而使用LLE方法反而使得准确率有大幅下降,这表明液压内泄漏特征数据属于线性分布而非流形分布,使用LLE方法保留下来的更多的是一些非敏感信息甚至是错误信息,而使用PCA提取主成分则可以有效提取重要信息,剔除非敏感信息。
对比K均值聚类和谱聚类诊断结果可以发现,在液压内泄漏故障诊断的条件下,K均值聚类有着很大的不稳定性,在不同场景下表现差异较大,而谱聚类则可以很好的适应不同零部件的内泄漏故障诊断。
此外,在液压内泄漏实验中通过阻尼孔和模拟磨损的方式来模拟泄漏量的大小,可以将泄漏量分层为多个层级,以液压缸泄漏分别用K均值和谱聚类进行诊断,分层数n,准确率η得到的结果如图6所示。

图6 分层数量对聚类效果的影响
从图中可以发现,随着分层数量的增加,准确率会有较大幅度的下降,这是因为在阻尼孔尺寸较小时,改变孔径大小对泄漏量的影响比较小,因此难以对低泄漏情况进一步分层,但从总体上看谱聚类在分层数不多时效果优于K均值聚类,且在分层数为3时取得最好的效果。
4 结论
(1) 本研究提出了一种基于时间特征分割和降维谱聚类的液压内泄漏故障诊断方法。时间特征分割使得降维谱聚类可以用于液压内泄漏的故障诊断,有效的解决液压数据阶段性变化和各阶段特征不同的问题。对特定阶段的数据提取时域和小波域特征后进行PCA降维,可以有效去除非敏感信息,提高谱聚类诊断的准确性。
(2) 针对液压内泄漏数据数量较少且可能泄漏位置多的特点,采用降维谱聚类的方法进行故障诊断,对数据量要求较低的同时在不同零部件上均可以达到不错的诊断效果,与其他无监督学习方法对比显示其同时具有稳定性和高准确率,是一种高效的故障诊断方法。
