求解非线性方程组的几种方法及程序实现

雍龙泉

(陕西理工大学 数学与计算机科学学院, 陕西 汉中, 723001)

考虑非线性方程组

(1)

记x=(x1，x2，…，xn)，向量函数F(x)=(f1(x)，f2(x)，…，fn(x))T，则方程组(1)等价于如下非线性方程

F(x)=0.

(2)

很多复杂的问题都可以转化为非线性方程组的求解问题，其最基本的求解方法是牛顿法[1-7]。近年来，相继出现了五阶牛顿迭代法[8]、七阶牛顿迭代法[9-10]、八阶牛顿迭代法[11-12]、九阶牛顿迭代法等[13-14]。对非线性方程组而言，牛顿迭代法需要计算偏导数矩阵，并依赖于初始点的选取和函数F(x)的性态[15-18]，而在一些实际问题中如何选取合适的初始点本身是一个比较困难的问题，因此使用牛顿迭代法时具有一定的局限性[19]。

本文假设非线性方程组的解存在，在给定初始点后，如何把数学公式转变为可以运行的代码，让初学者对编程不再望而生畏；进而提高学生编程的兴趣，最终能够利用程序对实际问题进行求解，培养与提高学生的科学计算能力。

下面通过一个具体的非线性方程组，分别给出其Jacobi迭代、Gauss-Seidel迭代、Newton迭代、五阶牛顿迭代；在给出迭代公式和初始点后，并分别给出了MATLAB代码和对应的计算结果。

算例分别用Jacobi迭代法、Gauss-Seidel迭代法、Newton迭代法、五阶牛顿迭代法求解如下非线性方程组

1 Jacobi迭代

Jacobi迭代法的迭代格式：

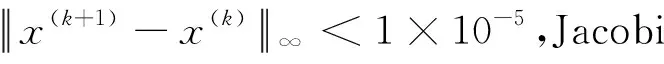
表1 Jacobi迭代法的MATLAB代码

表2 Jacobi迭代计算结果

2 Gauss-Seidel迭代

Gauss-Seidel迭代法的迭代格式：

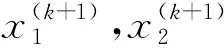
表3 Gauss-Seidel迭代法的MATLAB代码

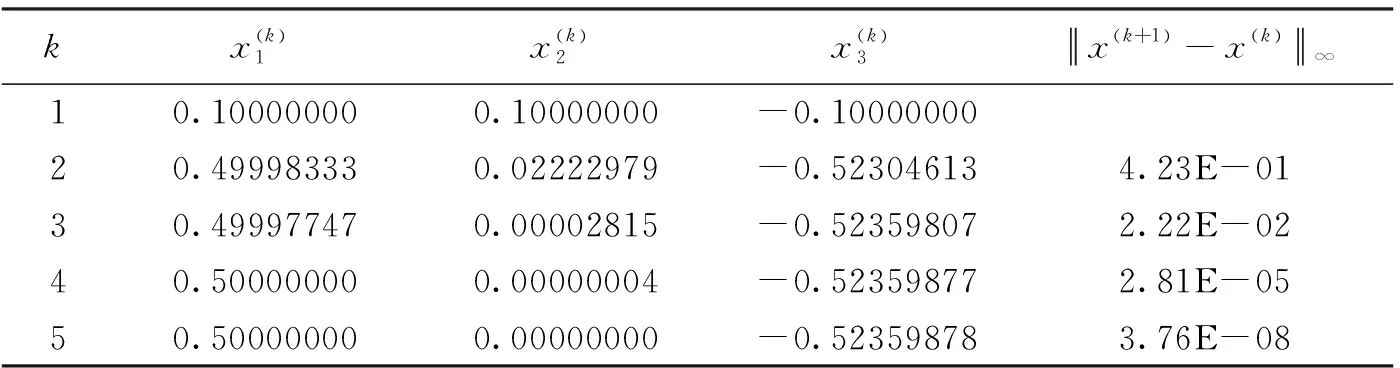
表4 Gauss-Seidel迭代计算结果

3 Newton迭代

Newton迭代法的迭代格式：

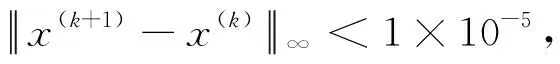
Newton迭代法要求矩阵F′(x)可逆，若F′(x)奇异或接近奇异，可以采用阻尼Newton迭代法进行处理。

表5 Newton迭代法的MATLAB代码

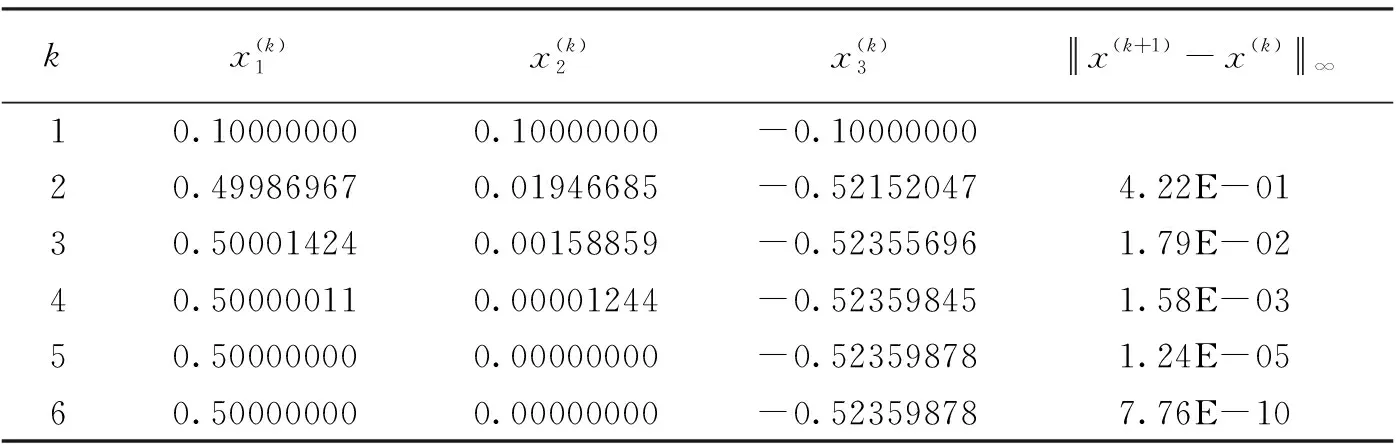
表6 Newton迭代计算结果

4 五阶牛顿法迭代

文献[20]中给出了五阶牛顿迭代法：

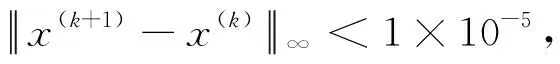
表7 五阶牛顿迭代法的MATLAB代码

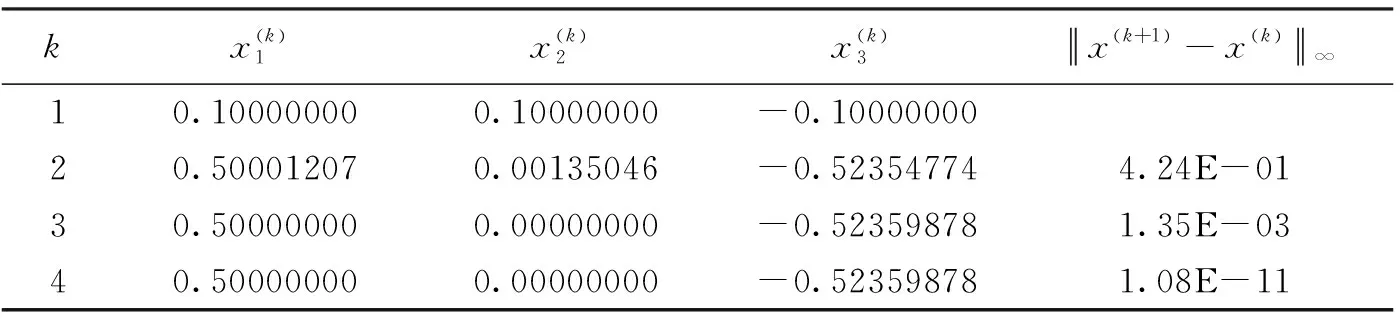
表8 五阶牛顿法迭代计算结果

需要求解的非线性方程组fun1与偏导数矩阵dfun1的代码见表9和表10。

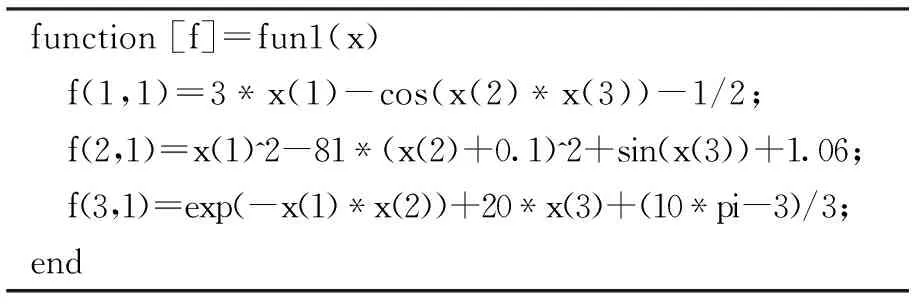
表9 非线性方程组fun1的代码

表10 偏导数矩阵dfun1的代码

文献[20-23]中分别采用该五阶牛顿迭代法求解线性规划、线性互补、非线性两点边值、投资组合优化等问题。

更多的实验结果表明：各类迭代的收敛与否、收敛快慢均与初始点的选取有关；收敛阶数越高，需要付出的计算代价(包括占用内存、函数调用次数)也就越大；即使高阶的牛顿法，也只有初始点与根很靠近时，高阶收敛性才能很好地体现出来。