人工智能时代下的工程优化教学改革研究

常甜甜，张建科，李小平，冯 晶

(西安邮电大学 理学院,陕西 西安 710121)

最优化理论是人工智能领域的有力技术方法之一。“工程设计中的最优化数学方法”(简称为“工程优化”)是研究生的公共课程，其在机器视觉领域、数据挖掘领域、人工智能领域发挥着愈来愈重要的作用。传统的数学教学手段是课件结合粉笔加黑板，教师以书本内容为主，枯燥地讲授数学的理论知识。“工程优化”是一门实用性极强的学科，这门课程的教学方法仍然停留在“概念-理论-计算”的传统教学模式，学生在学习的过程当中不知道如何将理论与实际结合起来，不知道学习的优化算法到底可以用来做什么？影响了学生的学习热情和创造性思维的培养。目前高校在教育教学过程中，不断的与时俱进，调整教学方法和大纲，以适应时代变化[1-13]。笔者所在最优化教学团队在教学内容和方法上进行改革，提出案例教学法，即“工程案例-建模-理论分析-问题求解”的教学模式。具体地首先给出一个浅显易懂的工程案例问题，且是该领域的研究热点问题，根据问题建立最优化模型，引导学生将最优化原理与各自专业中的研究对象相结合，最后采用最优化计算方法来求解问题，完成一个“问题-建模-理论-计算-应用”的完整流程，提高学生用最优化方法解决工程实际问题的能力。所选案例要紧扣教学内容，案例分析的目的是使学生加深对所学理论知识的理解和运用理论知识解决实际问题的能力，因此，所选案例必须是针对课程内容的。即案例内容具有一定的代表性和普遍性，具有举一反三、触类旁通的作用，而不是实践中根本不会发生的案例，且典型的案例往往涉及的关系比较全面，涵盖的法律知识较多，有助于学生从各个方面对所学理论加以验证，从中得出正确结论。因此，案例的选择应该具备真实可信、客观生动、案例多样化、相关性以及典型性。

1 实施方案

案例教学法，即“工程案例-建模-理论分析-问题求解”的四步教学模式。工程案例的引入可以采用具体模型(如最小二乘模型)，也可以采用实际应用问题(如图像重建)。以文献[13]为例，具体的工程案例设计举例如表1所示，从表1中的涉及教材内容方面可以发现，这几个工程案例涵盖了教材的全部内容，而且这几个工程案例是目前学科研究方向的热点研究内容。当将这些案例吃透后，理论问题自然而然产生，比如为什么初始点的选取会引起解不稳定？优化模型的光滑化问题？为什么单纯形法在可行域顶点达到最优解？优化模型问题的分类问题？带着这些理论问题引导学生进行进一步的定理证明及推导。

表1 教案设计涉及内容

2 教学方法举例

以医学图像重建[14]和模式分类[15-18]案例为例对案例教学法具体进行说明。

2.1 医学图像重建

2.1.1 医学图像重建背景

电阻抗图像重建问题遵循电磁场基本规律满足MAXWELL方程，其可以简化为准静态电磁场问题，满足Laplace方程[14]：

(1)

Laplace方程给出了模型参数(电导率)和测量参数(边界电压)之间的关系，已知电导率σ求电势φ称为正问题，已知电势φ求电导率σ称为反问题。有限元法(FEM)是求解电磁场问题的常用数值解法。FEM法需要将场域离散化，即将场域进行剖分，剖分后图像重建问题可以看作是以下线性方程组：

Jσ=φ

(2)

式中：J为Jacobian矩阵，σ为电导率分布，φ为边界测量电压值。

2.1.2 最优化模型建立

问题(2)是一个典型的欠定问题(ill-posed problem)， 可采用最小二乘法思想逼近其近似解， 即求解：

(3)

式中：Γ称为正则化矩阵(在很多情况下，取单位矩阵I)。 第一项为拟合度量， 第二项为正则项。p取不同值:0、1、2， 即得不同类正则化算法。L2范数的优点是目标函数光滑，求导计算方便， L2范数正则化的典型代表是Tikhonov正则化方法:

以下就问题(5)的求解问题进行讨论。

2.1.3 最优化算法理论分析

无约束优化问题的一般迭代格式[2]是:

σk+1=σk+λkdk

(6)

式中：λk是最优步长，dk是当前搜索方向，σ定义同上。牛顿法的步长是定长的，即λk=1， 搜索方向是:

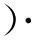
(7)

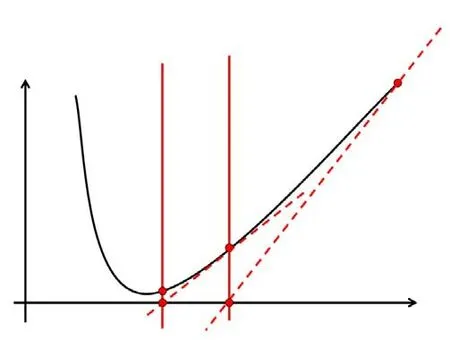
图1 牛顿法算法迭代点序列图示

式(7)是牛顿法算法的搜索方向， 点列迭代如图1所示. 因此只有Hessian矩阵正定时，牛顿方向才是下降方向。给定初始值点x0， 过点做切线与x轴相交， 以交点做垂线与曲线相交于点x1，以此类推即可得到牛顿法算法的迭代点列，直至达到收敛要求。但是，但目标函数曲线变化较大，或者初始值选取不当时，牛顿法算法可能不收敛。

图2 牛顿法算法初始点选取不当情况下迭代点列图示

假设图2目标函数f(x)的可行域为[a，b]， 图2(a)为目标函数曲度变化较大时， 取b点为初始点x0，经过几步迭代到x2，在x2点做曲线的切线可以发现x3点落到了可行域[a，b]外，因此这种情况下牛顿法算法不收敛; 图2(b)中如果初始点选取为a，则在下一步迭代时，点直接落在了可行域外，算法不收敛;但在图2(c)中，初始点选为b点，则x1落在了可行域内，算法收敛。由此，可以发现牛顿法算法对初始点的选取直接关系到算法的稳定性和收敛性。

在牛顿法算法中，每次迭代都涉及到目标函数的梯度dk和Hessian矩阵∇2f-1(σk)， 具体计算如下:

梯度函数为：∇f(σ)=2JT(Jσ-φ)+2ασ

Hessian矩阵为：∇2f(σ)=2JTJ+2α

牛顿法步骤描述如下:

输入:已知选定初始分布σ0，ε>0，k=0。

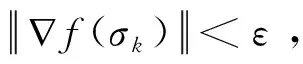
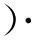
转向b)

b)计算σk+1=σk+dk，k=0， 转向a)

输出：σ*=σk+1。

2.1.4 最优化问题求解及应用实例

图像重建问题的正向问题计算借助EIDORS3.10软件[22]计算。具体的实验参数设置：目标选取三种情况， 成像目标在中心点位置， 成像目标在1/2半径处，以及成像目标在边界位置。电极总数为16个，接触阻抗值为0.005 Ω，电流强度为1 mA，背景电导率为0.0025 s/m，目标电导率为0.005 s/m，采用对向激励模式，仿真数据剖分单元格总数1968个，节点数1049个。

表2 牛顿法成像结果

提出问题：在实验中发现，如果初始点值为0.0015，牛顿法失效，代码出现报错，提示：Hessian矩阵必须为正定矩阵。从而引起学生对于下降类算法的证明以及为什么教材中要求Hessian矩阵为正的问题的思考。并引导学生对该问题的解决方法。

2.2 模式分类

2.2.1 模式分类背景

支持向量机(support vector machine, SVM)是一种数据挖掘新方法[17]，可以解决小样本问题、非线性问题以及高维数据等问题，且推广能力较强以及具有全局最优解。被广泛应用于综合评价、预测问题、数据拟合以及模式识别等问题。SVM模型基于极大间隔分类器的准则可推导获得，是一个凸二次规划问题，引导学生思考，如何求解该凸二次规划问题？

2.2.2 最优化模型建立

以线性可分情况下的支持向量建模为例，SVM的算法思想是在多个分类超平面中，基于极大间隔原则，找出其中的最优决策超平面，见图3。

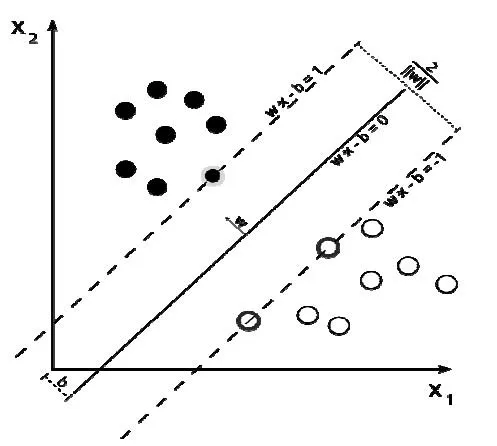
图3 极大分类超平面图示

引导学生并提问：在一个线性可分问题中可以存在多个分类面，如何使得该分类面确定且唯一？一个直观的方法就是采用极大间隔准则，如图3所示，找一个方向向量w，在方向向量的切向量方向取一条线，沿切向量方向移动该线，当该线触碰到正类样本则停止，继续向下平移碰触到负类样本后停止. 取这两个线中间线即为要找的唯一的分类线。该法则满足两类样本点间间隔最大原则。可以得到线性可分支持向量分类机原始问题为：

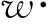
(8)

式中：xi为样本点，yi为样本对应标记，l为样本数，w和b为超平面方程参数。为使得分类问题可以引入核函数来处理非线性问题，将原始问题转化为对偶问题进行研究，此处就引入了对偶问题的理论。

2.2.3 最优化算法理论分析

此处可引入并讲解KKT条件和Wolf对偶理论，式(8)的拉格朗日函数为：

(9)

式中：α为拉格朗日乘子。由wolf对偶原理，求拉格朗日函数关于w，b的偏导数。可以得到：

(10)

代入(9)可得对偶问题为：

αi≥0，i=1， …，l

(11)

在最优化问题(11)的求解过程中涉及到工作集(working set selection)的选取问题，需要引入KKT条件，因此可以在这部分给学生仔细解释KKT条件的理论知识，本文不再赘述。设α*是对偶问题的任意解，则可按下式计算出原始问题的解：

(12)

2.2.4 最优化问题求解及应用实例[18]

为了让学生有更直观的理解，并测试所提出算法的有效性，实验数据来源于网络或者实际应用问题，例如：UCI数据库[23]，所选测试数据信息见表3。表4为SVM分类结果，评估准测为精度，即：

(13)

表3 实验数据描述

表4 SVM分类结果

在样例建模和求解过程中，引导学生思考在整个样例过程中需要进行哪些条件的判定？模式分类还有哪些应用？最优化模型的分类？停机准确的选取问题等等。

3 结论

“工程优化”是人工智能、数据挖掘、机器学习等热门研究领域的数学基础课程，但在实际教学中发现，按部就班的采用传统的教学方式时，学生并不能理解教材与实际应用问题之间的关系，以至于遇到实际工程问题后仍然不能解决问题。本教学改革方式采用案例教学法，通过引入各个学科的热点研究问题，针对热点问题进行建模、分析、求解，帮助学生搭建理论与实际之间的联系，提高学生解决实际问题的能力。