利用波动图进行驻波的位相和能量特征分析

吴波英，王军延*，付伯桥，彭晓星，陈 杰

(1.湖北工程学院 物理与电子信息工程学院，湖北 孝感 432000；2.湖北工程学院 化学与材料科学学院，湖北 孝感 432000；3.湖北工程学院 新技术学院，湖北 孝感 432000；4.湖北汽车工业学院 理学院，湖北 十堰 442002)

波动图是将某一时刻各点的振动情况定格在一张图形中，因此有人形象地将它称之为波的“照片”。利用波动图，我们可以直接判断质元的振动情况，也可以判断波传播引起质元的相对形变量的大小，这对于分析波的位相和能量特征十分方便，也同样适用驻波的情形。在教学中，笔者发现学生从驻波波动图分析波的位相和能量特征可能并不困难，最大的困难在于学生是否能自己绘制驻波波动图。

由于波的叠加实质是振动的叠加，因此教材一般采用在同一幅图上同时绘制相向传播的两列相干波的波动图，然后将两波在同一点的振动位移相加得到驻波的波动图[1]。杨庆怡等[2]提出一种利用振动旋转矢量和波动旋转矢量来描绘驻波波形的方法。该方法首先利用振动旋转矢量At确定驻波在时刻t的波腹，然后以波腹为长度的波动旋转矢量Ax作出这一时刻驻波的波形。王明美等[3]用“几何画板”绘制驻波的波动图。其中第一种方法[1]常用的教学方法，但是学生绘制一个行波波动图尚且困难，在一张图上同时绘制两个(相向传播)的行波波动图就更不容易了；第二种方法[2]确实具有一定的操作性，然而，学生理解这种方法也许有一定的困难，因此他们并不能熟练掌握这种方法；第三种方法[3]需要学生掌握几何画板软件，课堂教学中这显然不太现实。本文采用驻波表达式的振幅因子与简谐振动因子相乘的方法画出不同时刻的驻波波动图，笔者在教学过程中发现学生很容易掌握这种方法，并对他们理解驻波的位相和能量特征也有一定的帮助。

1 驻波表达式

在教材中，有两相干波分别沿x轴的正、负方向传播，假设两波在原点的振动表达式相同，即：

y0=Acosωt

(1)

则沿x轴的正负方向传播的两相干波为

(2)

式(2)说明任意点处存在两个振动，由振动的叠加原理，任一点处的振动为

(3)

2 绘制驻波在不同时刻的波动图

驻波表达式(3)可视为振幅因子与简谐振动因子两项之积，而t时刻的简谐振动因子对所有质点都相同，是0和1之间的一个“数字”，因此可以先画出振幅因子的图像，即振幅与坐标的关系，再与这个“数字”相乘得到某时刻t时各点的振动位移，即驻波某时刻t的波动图。

振幅与坐标的关系如图1中(i)所示。由于假设两波在原点的振动方程相同，因此原点就是干涉加强的点，即原点处为波腹。从图1中(i)可以清楚地判断出波腹(点O和与B、C两点的中点)与波节的位置(点A、B、C)。值得注意的是，这里曲线的起伏说明各点的振幅有大有小，但与行波波动图曲线起伏的意义不一样。行波中各点作同频率同振幅的简谐振动，行波波动图曲线的起伏表明同一时刻各点的振动位相或振动位移不同。

1)令t=0，第二项正好等于1，两项相乘的结果还是等于第一项，因此该时刻的波动图如图1中(ii)所示，这与图1中(i)完全相同。说明该时刻各点都处于各自的振幅处，即各点同时运动到各自正或负的最大位移处。由于各点作同频率的简谐振动，由振动的知识可知，当质点运动到最大位移处时，下一刻将向平衡位置运动，因此下一时刻各点均向各自的平衡位置运动。

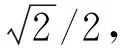
3)令t=T/4，第二项等于0，与第一项相乘的结果是该时刻各点的振动位移均为0，说明各点同一时刻均运动到各自的平衡位置，此时的波动图是一条位于x轴的直线，如图1中(iv)所示。由于各点做作同频率的简谐振动，由振动的知识可知，当质点运动到平衡位置时质点的速度最大，由于惯性下一刻各点将继续按原运动方向运动。因此，可以预测下一时刻的波动图可能的形式。

然后令t=3T/8，t=T/2，t=5T/8，t=6T/8，t=7T/8，采用同样的方法，可以分别画出对应时刻的波动图。当t=T时，各质点完成一次全振动，都回到t=0的位置，因此与t=0的波动图完全相同。

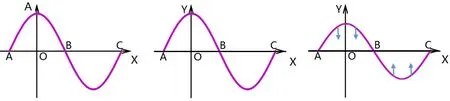
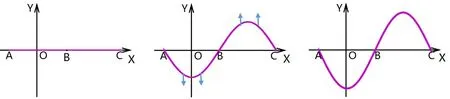
(i) 振幅与位置坐标的关系 (ii) t=0时刻 (iii) t=T/8时刻 (iv) t=T/4时刻 (v) t=3T/8时刻 (vi)t=T/2时刻 图1 驻波在不同时刻的波动图

从图1可以看出，驻波的波形曲线是一些高矮不同的余弦曲线，即不同时刻的波形并不相同。然而，我们在一根两端固定的、张紧的弦线上观察到的驻波是波形不随时间变化的波动[4]，这是由于视觉暂留才给人产生的错觉，因此称为“驻波”。

3 驻波的位相特征分析

由上面的分析可知，驻波中各点作振动范围不同的同频率简谐振动，只有波节是始终静止的点，可以看到这些始终静止的点将驻波分成了一段一段的，因此驻波可视为分段振动。相邻波节A、B之间各点在t=0时刻同时到达各自正的最大位移处，而在t=T/4时刻同时到达各自的平衡位置，因此这些点的振动是同步的，即振动同相。

波节B两侧的A-B与B-C之间各点，在t=0时刻分别达到它们各自正、负的最大位移处；在t=T/4时刻它们同时到达各自的平衡位置，但是A-B之间各点向负方向运动，而B-C之间各点向正方向运动，因此可以判断波节B两侧的这些点的振动反相。

从驻波表达式(3)也可以得到该结论。驻波表达式的振幅因子是有正有负的，如从图1中(i)所示，可以看出波节两侧各点的振幅异号，因此波节两侧各点的振动表达式实际上相差一个负号，这个“负号”即表明波节两侧各点振动反相。而相邻波节之间各点的振幅同号，即表明相邻波节之间各点振动同相。

4 驻波的能量特征分析

波的能量包含两部分：一部分是各质元由于振动而具有的振动动能，振动动能与速度的平方成正比。由于各点作简谐振动，振动速度与振动位移有关，如振动位移为0时，振动速度是最大的，其振动动能必然最大；如振动位移为±A时，振动速度为0，其振动动能必然为0。波动图记录了同一时刻各质元的振动位移，因此通过它可以直观地看出各质元的振动动能大小。

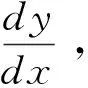
驻波虽然不是(行)波，但由于它也包含所有质元的振动，因此各质元必然有振动动能；由于它的波动图和行波一样也是余弦或正弦曲线，因此也会引起介质的弹性形变，因此各质元也必然有形变势能。

首先分析波腹和波节处的能量特征。从不同时刻的波动图可以看到波腹始终处于余弦曲线的极值处，即切线斜率始终为0，因此波腹处的形变势能时时为0；由于波腹处作振动范围最大的简谐振动，因此在波腹处总是具有振动动能，并且比非波腹处的质元同时刻的振动动能大。而波节是始终静止的点，因此波节处的振动动能时时为0；除了波动图为直线时(如图1中(iv)所示)，其他时候总处于余弦曲线斜率最大的位置，因此波节总具有形变势能，并且比非波节处同时刻的形变势能大。其余各质元均既有振动动能又有形变势能。

另外，波动图为直线时(如图1中(iv)所示)，此时各处的相对形变量均为0，说明此时各处的形变势能均为0；但此时由于各质点均处于平衡位置，各质点除波节外均具有振动动能，即此时能量以动能形式存在。质点处于平衡位置时速度为ωA，驻波中各点的角频率均为ω，而波腹处的振幅最大，因此其振动速度最大，振动动能必然最大。此时能量(动能)主要集结在波腹处。在t=0 (如图1中(ii)所示)和t=T/2 (如图1中(vi)所示)时各质点均到达各自的最大位移处，此时各质点的动能均为0，但此时由于除波腹外各处都存在弹性形变，因此各处存在形变势能，其中波节处的相对形变量最大，因此波节处的形变势能最大，即此时能量以势能形式存在，并主要集结在波节处。

从上面的分析可以看出波腹处的形变势能总为0，其动能随运动不断变化；波节处的动能总为0，其形变势能随运动不断变化。并且当波腹动能最大时，波节处形变势能为0；波腹动能为0时，波节处形变势能最大。

文献[5]通过两相向传播的波的能流密度相减得到驻波的能量密度，发现波节、波腹位置上的能流密度无论什么时刻均为0，但除波节、波腹外，其他各质元的能流密度可以不为0，说明能量在波节、波腹之间的各质元上流动。换言之，由于存在波节(始终静止的点)，因此驻波的波形曲线并未像行波那样移动，因此能量也并未像行波那样定向传播，能量只是在波腹和波节处往返集结。

5 结语

1)驻波表达式(3)中的简谐振动因子是0-1之间的一个“数字”，因此先画出振幅因子的图像，再与这个“数字”相乘，就可以很容易地画出不同时刻的驻波波动图。

2)驻波的位相特征：相邻波节之间各点振动同相，而波节两侧的各点振动反相。

3)驻波的能量特征：当波动图为直线时，此时各质元除波节外只有动能，形变势能均为0，并且波腹处的动能最大；在t=0和t=T/2时刻，各质元除波腹外只有形变势能，动能均为0，并且波节处的形变势能最大。其他时刻除波腹和波节外的各质元既具有动能也具有势能，动能和势能随着运动不断变化。驻波的能量没有向外传播，但在波腹和波节之间各点流动。