考虑防渗帷幕的平原水库渗流分析大井法研究
2021-06-16王维平徐巧艺曲士松
王 琛,王维平,徐巧艺,刘 振,曲士松
(1.济南大学 水利与环境学院,山东 济南250022;2.济南市清源水务集团有限公司,山东 济南250014;3.济南市玉符河管理中心,山东 济南250022)
黄河下游冲洪积平原地区水资源短缺,建设平原水库可在时空上有效调蓄黄河水,满足城市生活和生产用水的需求。平原水库为浅碟子形状,占地面积大,围坝长,一般半挖半填,受水文地质条件、防渗措施和施工技术的影响,存在易渗漏的问题。水库渗流会影响区域天然流场,从而改变地下水的补给径流条件[1]。因此,水库渗漏量的计算一直是平原水库供水安全关心的重要问题,以往水库渗漏量计算多以达西公式为主,达西定律方法简单,适合估算,但对于截渗帷幕作用下的渗流问题不能很好地处理。
众所周知,达西定律奠定了地下水渗流力学的基础[2-3]。裘布依根据潜水面的坡度角都很小的现象,提出了著名的裘布依假定,并以达西定律为基础提出“圆岛模型”条件下的地下水稳定流计算公式[4-6]。鲍切威尔在前人研究成果的基础上提出了大井法,主要用来估算群井干扰下的涌水量[7]。国内大井法的研究与应用已经相当成熟,目前主要用于处理基坑、矿道降水问题。在应用大井法时通常不考虑截渗帷幕的作用,但实际上地下水经由含水层流入基坑的过程中截渗帷幕的存在使得过水断面突然变窄,并且水流在含水层中作水平运动流入基坑后在抽水的作用下作垂直运动会产生局部水头损失。胡静[8]针对二元结构土层进行了深基坑降水模型试验和悬挂式帷幕渗流模型试验,验证了帷幕的挡水作用可以减少工程降水对周边环境的影响。张邦芾[9]采用模型试验箱,探讨了帷幕插入深度、过水断面厚度、水头差对坑外水位降深及流量的影响规律,结果表明坑外帷幕处的降深随帷幕插入深度的增加而减小,但减小的幅度随插入深度的增加而变缓,而流量则随帷幕插入深度的增加而略有减小。刘仲秋等[10]对平原水库坝基渗流计算范围的研究中还发现,悬挂式截渗墙使得坝基底部透水不但导致渗漏量增加,而且使得浸润线整体抬高,影响范围增大。王军辉等[7]结合达西定律处理截渗帷幕处的绕流问题,推导出了有截渗帷幕干扰下的修正大井法和降水曲线。骆冠勇等[11]在仅考虑水平渗流的情况下用数值方法计算了由悬挂式阻水结构引起的水头损失。李旺林等[12]提出了承压-潜水含水层完整反滤回灌井的稳定流计算公式,通过水量平衡解决了回灌过程中的水头损失计算。这些研究都表明截渗帷幕对水流存在干扰作用,但并没有给出水头损失解析法的处理方式,而传统大井法采用的方程计算水库渗流时,不能计算截渗帷幕造成的水头损失。本文研究平原水库渗流的解析计算方法,结合大井法和阻力系数法进行回灌公式的推导,为水库渗流的解析计算提供了新的方法和处理思路,解决了受截渗帷幕干扰产生的水头损失的计算问题,使大井法的渗流计算模型更合理。
1 水库渗流大井法模型
水库渗漏与回灌井具有相似之处,截渗帷幕的作用使得水库水向下作垂直渗流运动,到达坝基相对隔水层后在水库内外压力差作用下向库外运动并在截渗帷幕处发生绕渗,见图1。在裘布依假定下,大井法处理降水问题时,坑道系统被视为一个大井,坑道系统圈定的面积相当于大井的面积,进而应用裘布依稳定流基本方程可以近似计算整个坑道系统的涌水量和降水曲线。基于以上启发,我们以具有悬挂式截渗帷幕的水库为例,将水库看作稳定向地下注水的大井,以相似的方式解决水库渗流计算问题。
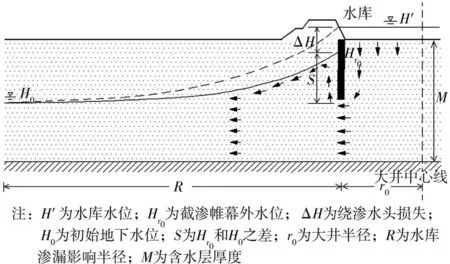
图1 水库渗漏大井法示意
1.1 模型概化
对于拥有悬挂式截渗墙的平原水库,在渗透性能良好、均质各向同性的有限深水平潜水含水层中,假设水库渗流达到稳定状态且符合达西定律,忽略地下水运动的垂向分速度,即地下水运动满足裘布依假定。利用面积相等的方式将水库概化为等面积的大井。采用截渗帷幕的平原水库,一般截渗墙的截渗深度在第一个稳定的隔水底板之上,因此从大井的类型来看属于潜水井。
1.2 水库渗流大井法基本方程
与传统大井法的渗流方式不同的是,平原水库为地面建筑物,水体在地表之上,水流穿过井壁由含水层向周围扩散之前需要先经过垂向渗流,然后经过截渗帷幕阻挡,因此截渗帷幕内外存在一个水位差,即

如图1所示,应用面积相等的原理概化后的大井半径为

式中:F为水库水面面积,m2。
水库渗漏对周围地下水位有明显的抬升作用,其影响半径用R表示。根据水量平衡原理,截渗帷幕外各个过水断面流量相等:

式中:r为影响半径范围内任意一点到水库截渗帷幕的距离,m;h为地下水位;k为渗透系数,m/d。
对式(3)进行积分:
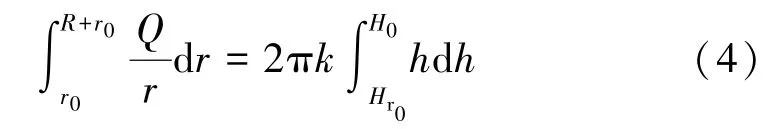
积分后得到有关水库渗漏量的计算方程:
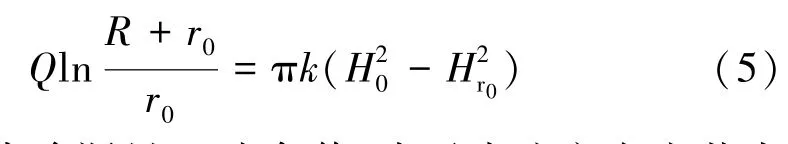
式(5)中渗漏量Q为负值,表示水流方向由井内向井外运动。为了应用方便,我们对其取正值并进行相应变换,令S=Hr0-H0,得到水库渗流大井法方程:
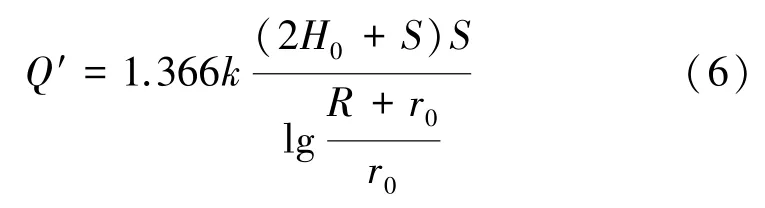
式中:Q′为无截渗帷幕时的水库渗漏量,m3/d。
1.3 截渗帷幕影响下的渗流方程
由式(6)可知,在水库渗流计算中需要知道S,因存在渗流水头损失,截渗帷幕内外的水位升幅是不同的,故:

在计算渗流水头损失ΔH时借鉴船闸工程中常用来处理透水闸室地基绕渗的改进渗流阻力系数法,该方法计算准确,在我国船闸建造中应用广泛[13-14]。因为水库水面面积巨大,可以忽略r0和截渗帷幕厚度对渗流的影响,所以在应用此方式时将渗流过程分为进口段和出口段,如图2所示。各段的水头损失可以表示为
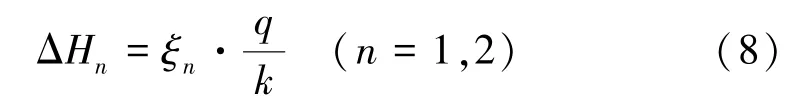
式中:q为单宽流量,m2/d;ξn为阻力系数,无量纲,仅与渗流区域的几何形状有关。
在船闸设计中进口段阻力系数计算式为
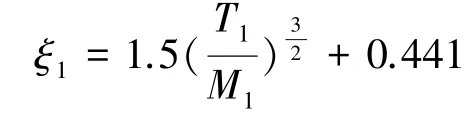
出口段阻力系数计算式为

考虑到平原水库并不需要深挖基坑,可认为M1=M2、T1=T2,因此ΔH可以表示为
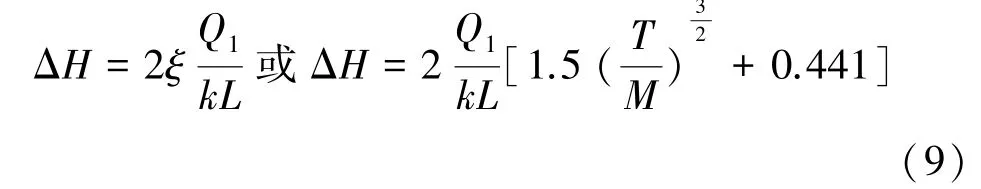
式中:Q1为截渗帷幕影响下的水库渗漏量,m3/d;L为围坝长度,m;T为截渗帷幕截渗深度,m;ξ为渗流阻力系数,无量纲;M为含水层厚度,m。
将式(7)、式(9)代入式(6)得到截渗帷幕干扰下的水库渗流大井法方程:
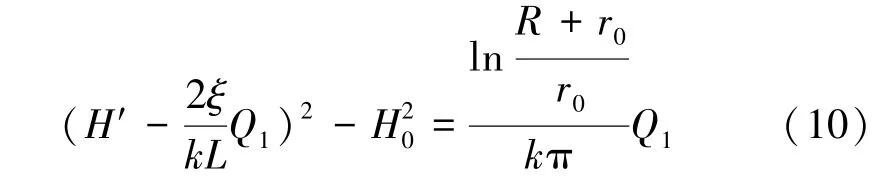
可以看出Q1前的系数皆为常数,因此令,则式(10)可以简化为
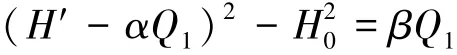
1.4 水库渗漏地下水壅水曲线
截渗帷幕对水头的削弱作用使得水库渗流壅水曲线也发生了变化。
不考虑截渗帷幕影响的水库渗漏地下水壅水曲线方程为
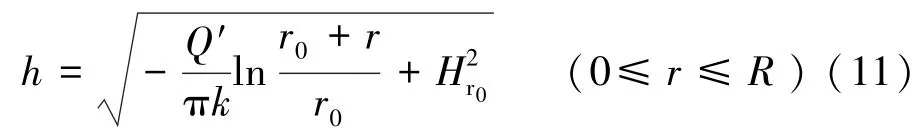
考虑到实际情况下截渗帷幕和水头损失的影响,整理式(1)、式(9)、式(11)得到截渗帷幕影响下的地下水壅水曲线方程:
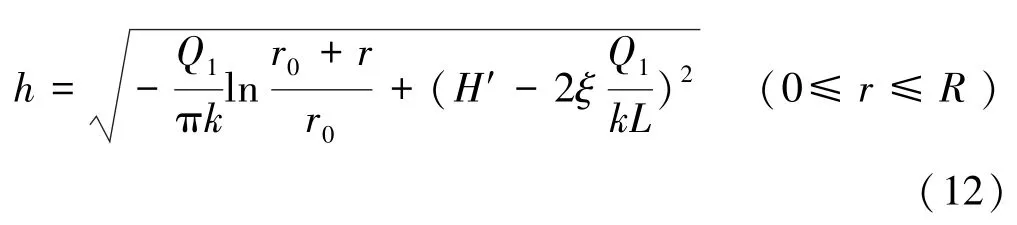
2 实例分析
以北方某引黄平原水库为例,应用上述水库渗流大井法分析水库渗漏及其对周围的影响,并进一步分析悬挂式截渗帷幕在水库防渗方面的作用。
该水库设计总库容4 850万m3,兴利库容为3 630万m3,正常蓄水位38.85 m,死水位31.1 m,围坝长度9 639.5 m,最大水面面积4.94 km2。坝体采用均质壤土坝和裂隙黏土心墙坝,并在上游坡铺设复合土工膜防渗,坝体整体防渗性能满足要求。围坝采用0.2 mm厚的PE薄膜垂直铺塑嵌坝基,最大铺塑深度16 m,为悬挂式防渗帷幕。该水库是典型的平原水库,其建设时采用悬挂式截渗帷幕,由于下部隔水层分布不均,截渗深度有限,因此导致水库建成后渗漏量大,当水位维持在31.1~35.0 m时,日均渗漏量为9万m3。
2.1 地质资料
该水库位于山前冲积、洪积扇与黄泛冲积平原交接的低洼地带。库前库区地面高程29.0~31.0 m,库区以西至黄河一带地面高程29.6~30.7 m。水库东北部地面高程一般为29.1~29.6 m,地势平坦。
根据现场抽水试验所得到的资料,库区周边土壤性质如下:第一层为厚度3.15 m的壤土,渗透系数k=2.22 m/d,给水度μ=0.13;第二层为厚度5.35 m的中细砂、砂壤土、粗砂粒层,k=3.56 m/d,μ=0.15;第三层为厚1 m的壤土,k=1.4 m/d,μ=0.13;第四层为粗砂砾石,厚度16.98 m,渗透系数k=48.51 m/d,μ=0.2;第四层以下为壤土,该层控制深度在30 m以上,渗透系数很小,可作为底部隔水边界。
2.2 地层概化
在处理水库渗漏问题时,因为第四层粗砂砾石渗透性极强且厚度大,是发生渗流的主要地层,所以为方便问题的处理,将多层土壤概化为一层均质土壤,并引入等效渗透系数和等效给水度的概念。
等效渗透系数计算公式为

式中:K为非均质含水层的垂向等效渗透系数,m/d;H i为第i层土壤的厚度,m;k i为第i层土壤的渗透系数,m/d。
假设第i层土壤的给水度为μi、厚度为Hi,第i层土壤全部疏干时单位面积土层释放的水量为μi H i,当各土层全部疏干时其释放的总水量可以表示为∑μi Hi,因此平均给水度可以表示为
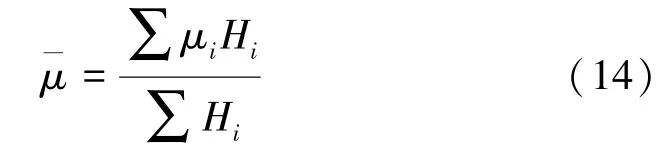
经过计算,概化为一层均质土壤的含水层平均渗透系数K=44.5 m/d、平均给水度为0.18。
2.3 渗漏计算
取水库现状运行水位H′=34.76 m和正常蓄水位H′=38.86 m分别计算。应用水库渗流大井法方程之前需要先计算水库渗漏的影响范围,即影响半径R。在大井法应用于基坑降水时,根据基坑所在含水层的性质可以分为潜水和承压水两种来计算基坑降水的影响半径R,平原水库水体在地表,不同于以上两种情况,采用排水沟影响半径计算公式:

式中:W为降水补给强度,m/d;t为周期蓄水时间,d,长期蓄水取365 d。
联立式(2)、式(9)、式(10)、式(15)求解不同情况下的渗漏量,计算参数见表1。
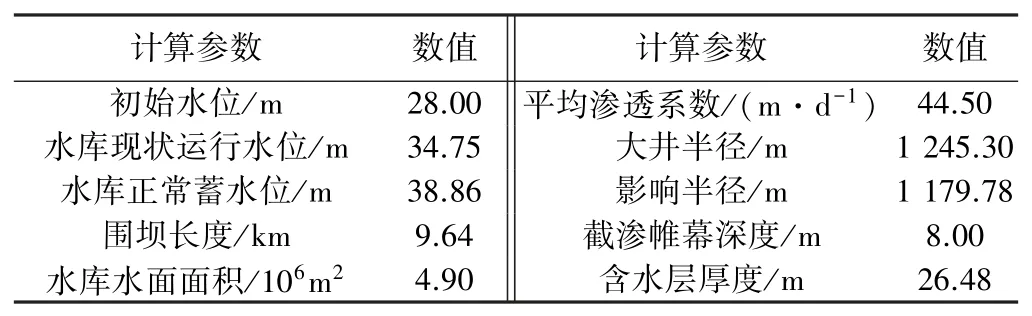
表1 水库渗流大井法计算参数
水库渗漏量计算成果见表2。

表2 水库渗漏量计算成果
2.4 壅水曲线
壅水曲线可以反映水库渗漏对周围地下水位的抬升作用随距离的变化情况,截渗帷幕会在一定程度上削弱渗漏对水位的抬升作用,因此计算水库渗漏壅水曲线时分为以下4种情况:①水库水位H′=34.75 m,考虑截渗帷幕的作用;②水库水位H′=34.75 m,无截渗帷幕;③水库水位H′=38.86 m,考虑截渗帷幕的作用;④水库水位H′=38.86 m,无截渗帷幕。绘制不同条件下水库渗流壅水曲线,见图3。
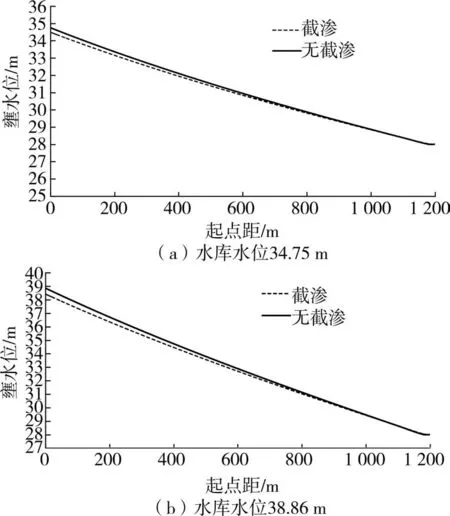
图3 水库渗流壅水曲线
2.5 拟合分析
计算结果显示现状条件下水库渗漏量达8.5万m3/d,与实际日均渗漏量约9万m3相符及与该水库除险加固工程设计报告中的计算和统计值相印证。为了进一步检验计算的合理性,共选取了库区周围4个不同距离的监测点对渗漏壅水情况进行验证。根据库区周边流场特点选取的4个监测点位于水库的东南方向即天然地下水流向的下游,以减少其他水文地质要素对观测的干扰。
2018年7月对水库进行野外实地测量,选取水库东侧距坝踵约1 300 m的河道水位作为初始地下水位。根据实测结果,水库水位为34.48 m时,周围地下水位为28.32 m。计算水库渗流壅水曲线并与各观测点水位进行拟合。拟合结果显示相关系数为0.96,壅水曲线能够反映受水库渗漏影响导致的地下水位变化趋势,证明计算方法具有合理性。
3 渗漏分析
库水位为34.75 m时由防渗帷幕造成的水头损失为0.26 m,截渗量为0.38万m3/d;库水位为38.86 m时水头损失为0.44 m,截渗量为0.73万m3/d。可见,目前水库的防渗帷幕在削弱渗流水头、抑制地下水位上升方面发挥的作用非常有限。究其原因,截渗帷幕平均深度约8 m,只占含水层总厚度的30%,且截渗帷幕深入下部粗砂砾石层较浅,效果非常有限。以往研究表明,当悬挂式防渗墙插入深度大于70%时,内外水头差明显增大[15-16],或者截渗墙穿过弱透水层后坝基渗流才显著下降[17]。由此可见,防渗工程设计不合理是造成此类平原水库渗漏大的主要原因。
可以看出,即使在有截渗帷幕并且低水位运行的条件下水库的渗漏量依然非常大。由图3(a)可知,现状运行水位下距离坝踵600 m的范围内壅水位高于区域平均地表高程,存在土地浸没的风险,实际情况库区周围500~1 000 m范围内确实存在大面积土地浸没,现已改造为人工湿地。
不同水库水位与浸没范围的关系见图4,可以看出如果水库水位维持在正常蓄水位38.86 m,那么库区周围约800 m以内的范围有浸没的风险。水库渗漏量受水库水位影响非常大,当水库水位达到正常蓄水位38.86 m时,库水位上升4.11 m,渗漏量增加5.99万m3/d。经计算,渗漏量与水库水位近似为直线关系(见图5),由此可见降低运行水位是减少渗漏量的有效措施。
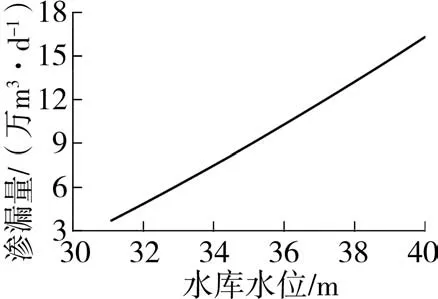
图5 渗漏量随水位的变化
4 结 论
在研究平原水库渗漏问题时提出了一种以裘布依假定为基础同时考虑截渗帷幕作用的平原水库渗流大井法,该方法建立于采用悬挂式截渗墙的围坝式平原水库,可用于分析渗透性能良好的有限深均质各向同性水平潜水含水层稳定渗流问题。以北方某引黄平原水库为例,应用该方法计算表明,平原水库渗流大井法能准确计算水库的渗漏量,并且渗漏量和水库水位近似为直线关系,水库水位越高渗漏量越大,降低运行水位是减少渗漏量的有效措施。由于该水库截渗帷幕截渗深度不足,因此实际截渗效果并不理想,现状条件下截渗帷幕每天的截渗量只有0.38万m3,当前截渗帷幕并不能有效防止周围地下水位上升。
对于计算深度内有多层介质含水层需要概化,存在隔水层或局部隔水的情况,以及无限深地基的情况,该方法的适用性还有待深入研究和检验。
