16 m无筋预应力UHPC简支工字梁抗弯性能足尺模型试验研究

王卫锋，陈健锋，郑小红*，范学明，田月强

(1.华南理工大学 土木与交通学院，广东 广州 510640；2.中路杜拉国际工程股份有限公司，广东 广州 510600)

超高性能混凝土(ultra high performance concrete，UHPC)是一种新型纤维增强水泥基复合材料，因具有高强、高韧和极好的耐久性优势[1-4]，在土木工程中具有广阔的应用前景。钢纤维的掺入，抑制了裂缝的发展，大大提升了UHPC结构的抗裂、抗剪性能，使UHPC梁的破坏模式从脆性剪切破坏转变为延性弯曲破坏[5-7]。无筋预应力梁是一种利用UHPC材料本身的抗剪性能，仅配置纵向预应力筋抗拉的新型结构。相比于传统钢筋混凝土预应力结构，无筋预应力UHPC梁减少了普通钢筋骨架制作工作，施工方便、快捷，成为UHPC结构发展的趋势。作为一种新型结构，抗弯性能是无筋预应力UHPC梁最关注的首要问题。

国内外少数学者对无筋预应力UHPC梁进行了抗弯性能的研究。2001年，美国联邦高速公路管理局(federal highway administration，FHWA)通过采用蒸汽养护条件制成了含钢纤维量为2%且长达24 m的预应力活性粉末混凝土(reactive powder concrete，RPC)梁，该梁仅配置了预应力筋，进行加载试验，该梁表现出了良好的力学性能，当挠度达到300 mm时，并没有找到肉眼可见的裂缝，同时其抗压强度达到了207 MPa[8]。2003年，VOO、FOSTER等人也同样对7根预应力RPC无腹筋梁进行了抗剪试验[9]，结果表明，钢纤维的含量以及类型对开裂荷载影响不大，仅对极限荷载有影响，破坏时，腹板形成了许多细小的裂缝，裂缝分布较均匀，破坏荷载是开裂荷载的两倍以上。2018年，RIDHA、SARSAM等人通过静力试验对无腹筋RPC梁的抗剪性能进行研究，得出即使没有配置腹筋，RPC抗剪承载力仍然得到提高，安全储备满足要求[10]。国内相关研究处于初步探讨阶段，2018年，李志南[11]以某主厂房屋24.54 m的无筋预应力UHPC工字梁为研究对象，采用SOFISTIK有限元软件进行计算分析，依据《活性粉末混凝土结构技术规程》[12]进行了理论计算，并进行该梁的足尺模型静载试验，结果表明：试验梁在荷载标准组合和基本组合作用下的试验应力值相比有限元计算的小很多，但在1.6倍基本组合下，应力值基本吻合；试验梁的极限承载力达到2倍荷载基本组合设计值。

世界上第一座无筋UHPC公路桥——瓦朗斯堡(Bourg-Lès-Valence)桥，于2001年在法国瓦朗斯堡建成，该桥采用π型板梁一体式结构，除了节段拼装位置存在普通钢筋外，并无配置其他普通钢筋[13]。2005年，美国首座无筋预应力RPC公路桥——马斯希尔桥(Mars Hill Bridge)在爱荷华州建成通车，该桥为跨径33.53 m的简支梁桥，由3根预制T形梁拼接而成，完全依靠钢纤维来抵抗剪力[14]。2015年，在马来西亚建成了目前世界上单跨最大的无筋预应力UHPC箱型梁公路桥——Batu 6桥，该桥单跨跨径达到100 m，主梁包括40个预制节段，通过纵向体内、体外预应力拼装而成，UHPC的使用使得全桥结构自重相比普通钢筋混凝土桥减少了50%[15-16]。

可见，相比于工程实践的应用，无筋预应力UHPC梁的抗弯性能研究相对不足，尤其是关于足尺无筋预应力UHPC梁承载性能的试验数据极少。本文将依托国内第一座无筋预应力UHPC梁桥——广州北环高速扩建F匝道桥，以其16 m无筋预应力UHPC工字梁为研究对象，通过四点弯曲下的足尺模型试验，对无筋预应力UHPC简支梁的抗弯性能展开研究，并与有限元计算值进行对比，以探讨该新型结构的受力性能及破坏机理，为无筋预应力UHPC梁在工程中的推广应用提供依据和参考。

1 试验方法

1.1 试件尺寸

试件依托广州北环高速扩建F匝道桥工程，该项目在国内首次采用跨径L为16 m的无筋预应力UHPC组合梁。预制梁由中路杜拉公司负责浇筑，同时制作一片完全相同的试验梁，如图1所示，包括下部的UHPC工字梁和上部C50混凝土桥面板两部分。UHPC工字梁高62 cm，顶、底缘宽度40 cm，跨中腹板厚度10 cm，到梁端部1.5 m范围内渐变到宽度为40 cm。工字梁顶设置15 cm厚，宽度为145 cm的现浇C50混凝土桥面板，板内配置了C16钢筋网。为了增强与现浇板的抗滑移能力，UHPC工字梁与桥面板之间通过C16的π型钢筋连接。UHPC工字梁内未配置任何纵向钢筋及箍筋，仅在上下缘各配置一束规格分别为4φs15.2和19φs15.2的1 860级有粘结预应力钢绞线。

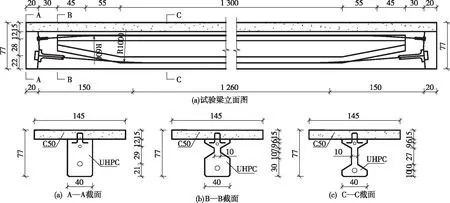
图1 模型梁立面图及横截面

1.2 材料

试验梁制作过程中，预留UHPC方体抗压试块、轴心抗拉试块，与梁同条件养护，28 d龄期后，进行试验，UHPC的立方块抗压强度平均值为167.9 MPa，抗折强度平均值为43.3 MPa，弹性模量为45 GPa，密度为2 450 kg·m-3，泊松比为0.2。

1.3 加载及测试方案

1.3.1加载方案

采用四点对称分级加载方式，加载点距离梁中心线各2 m，如图2所示。

加载过程分为两大步：第一步，预加载，以消除试验装置和梁体的非弹性变形。按照估算的开裂荷载的50%进行分级预加载(P1=150 kN)，每级30 kN，加载完成后持荷5 min；预加载完成后，在分级进行卸载。第二步，正式加载。每30 kN为一级进行加载，每级持荷10 min；加载至跨中出现第一条裂缝时，更改加载步长为10 kN，以控制脆性破坏的突然发生，每级荷载10 min；出现下列情形之一，停止加载并按步长卸载：①施加的荷载降至记录到的最大荷载值Pu的80%以下；②混凝土裂缝宽度超过1.5 mm；③其它会危及到安全的情况。

1.3.2位移测点布置

如图2(a)所示，共布置7个位移测点(S1—S7)，其中S1为跨中挠度测点，S2，S3，为四分点处，S4和S5为支座竖向位移测点。S6，S7，S8位于UHPC梁顶和C50桥面板截面处，以测量工字梁与桥面板间的滑移。

1.3.3应变片测点布置

如图2(b)，为了观察应变沿着梁高度的变化规律，跨中截面在UHPC工字梁和C50混凝土桥面板表面对称布置应变片(测点16—测点31)；为观测初始裂缝的产生，在梁底纯弯段范围内每隔5 cm沿梁纵向均匀布置应变片(测点1—测点15)。

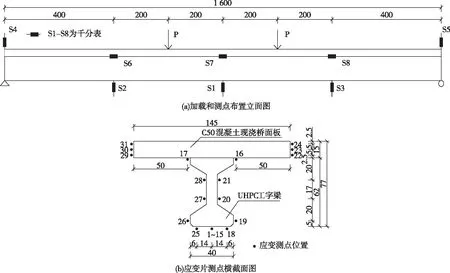
图2 试验加载及测点布置图

1.3.4测试装置

试验主要测试的量包括梁跨中以及L/4截面的位移、界面滑移；跨中截面应变、开裂荷载、极限荷载以及裂缝产生及开展情况。挠度由数显千分表进行测量，应变数据以及千分表测量值由DH3816N静态应变仪自动采集，荷载值由压力传感器测量，加载现场如图3所示。

图3 试验照片

2 试验结果

2.1 破坏形态

正式加载至300 kN前，应变、挠度等指标均呈线性增长，构件表面也未发现有裂缝。当加载至300 kN时，梁跨中截面底部部分应变测点突然出现急剧增长，显示出现初始微裂缝，此时跨中挠度为45.6 mm。随着荷载持续增大，纯弯段内弯曲裂缝逐步增多，裂缝逐渐由下翼缘向腹板顶部发展，裂缝细而密(如图4所示)，裂缝宽度增长并不明显；至试验结束，最大裂缝宽度发生在跨中附近截面，宽约为0.2 mm，且在裂缝最大宽度附近，梁表面有蜂窝现象存在，对裂缝宽度存在影响。其余裂缝宽度较小，大多保持在0.02 mm左右。

图4 裂缝分布

当加载至540 kN时，在加载点外侧的弯剪区出现明显斜向剪切裂缝；此时纯弯段内裂缝数量已相当多，跨中挠度为156.1 mm，相应矢跨比为1/103。考虑到最大裂缝宽度达到规范允许的0.2 mm，且梁挠度较大，停止加载，将540 kN定义为此次抗弯试验的极限荷载。

在整个加载过程中，并未观测到桥面板与UHPC 间有明显滑移，滑移测点数据显示加载至540 kN时，跨中位置滑移量极小，为0.024 mm。加载到90 kN后，梁体偶尔传出轻微的响声，应是后张法预应力钢束出现扭转搭接，加载时出现滑移，加载进一步拉紧而发出响声。

2.2 荷载-位移曲线

根据跨中测点S1所测挠度经支座测点S4和S5位移修正后，即为跨中实际挠度。图5 给出了单点荷载-跨中挠度(P-Δ)相关曲线，图中还列出了设计单位按弹性理论提供的计算值。

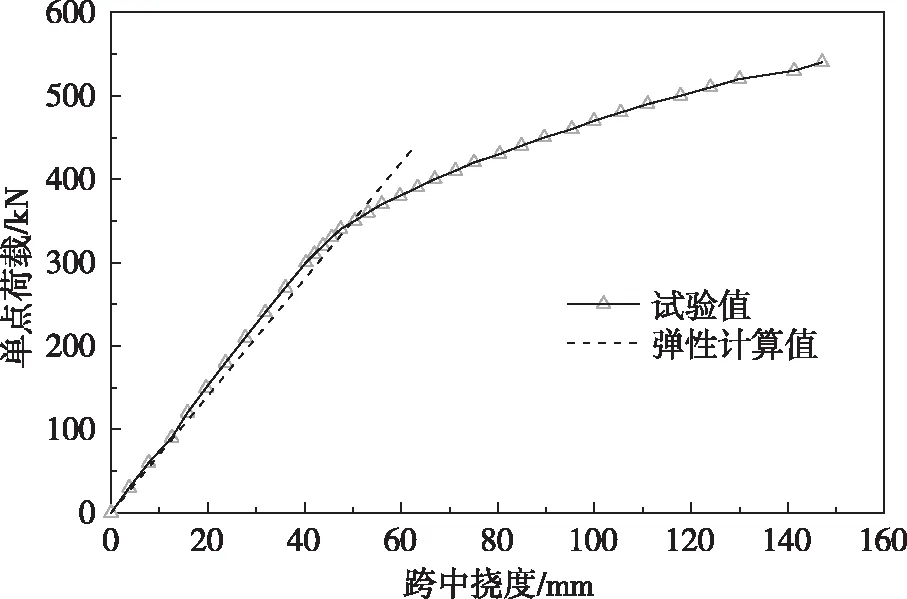
图5 跨中荷载-位移曲线

可见，试件在加载至开裂荷载(300 kN)之前，P-Δ曲线基本为线性直线段，且刚度与有限元弹性计算值吻合较好；达到开裂荷载之后，随着荷载值增大，裂缝迅速出现与发展，刚度出现大幅度退化，P-Δ曲线出现明显拐点；至加载至380 kN左右之后，刚度退化速率基本保持稳定，P-Δ曲线接近直线。

2.3 UHPC 工字梁与桥面板之间的相对滑移

在整个加载过程中，并未观察到桥面板与UHPC间有明显滑移。滑移测点数据同样显示两者相对滑移值较小，加载至540 kN 时，跨中位置S7滑移量为0.024 mm，弯剪段L/4处S6和3L/4处S8，滑移量分别为0.02 mm 和0.05 mm。图6为试验中采集的跨中S7测点荷载-UHPC 梁与桥面板之间的相对滑移的相关曲线。由图可见在加载初期，相对滑移的发展与荷载基本线性关系；在达到开裂荷载后，则呈阶梯状增长。直到试验结束，跨中(S7)相对滑移的总量仅为0.024 mm；且通过对比靠近梁腹板的桥面板板底测点17与梁腹板顶部测点21的应变值(见图6)，发现两者在加载过程中增幅基本一致，这与所测得的微小滑移量一起说明，连接UHPC与桥面板的抗剪键起到了很好的作用。

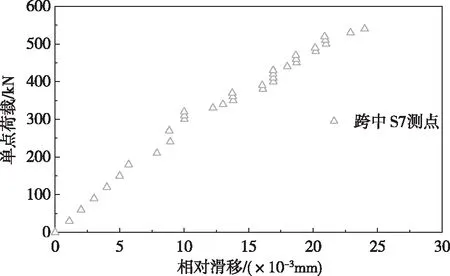
图6 UHPC工字梁与桥面板之间荷载-相对滑移曲线

2.4 应变

2.4.1UHPC梁底应变

从理论上分析，均布在纯弯段底部的应变测点应有相同的响应，但由于混凝土材料存在离散性，试验中裂缝开展情况与所测应变均存在不同程度的差异。图7给出了以50 mm为间距均布在UHPC工字梁梁底中轴线上的应变测点1—测点10的荷载-应变相关曲线。

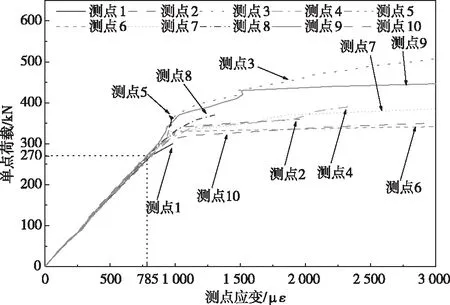
图7 UHPC工字梁底应变分布

考虑到当裂缝开展后，应变片所测数据不仅包含混凝土的弹塑性变形，还包括了因裂缝宽度发展产生的变形，因此在图7中舍去了在下一级加载时，应变增长到超过3 000 με的数据点，取其本级加载时的应变作为该测点最大应变。可以看出：(1)在荷载值达到270 kN、应变增长至785 με 之前，各测点均处于弹性阶段，离散性很小；(2)在加载至270～330 kN 这个区间，多数测点的相关曲线刚度迅速衰减，反映出该测点已有较大塑性变形甚至已形成裂缝；少数测点(测点03、09)刚度退化较慢甚至略有增长，原因是在其附近已有裂缝产生，致使其应变增幅变缓；(3)加载至360 kN 之后，部分测点应变迅速增长至20 000 με以上，如测点01、02、04、05、08，显示这些测点应变片已被裂缝穿过，所测数据实质上以裂缝宽度为主；其它测点应变则保持缓慢增长，如测点03、06、07、09、10，其应变增幅与弹性阶段相比要大许多，这反映了进入弹塑性段之后，试件截面抗弯刚度虽有较大衰减，但仍有继续承载的能力。

2.4.2梁截面高度范围内应变

通过对比各级荷载下UHPC梁不同高度截面上应变的分布，可以清楚截面上应变状态的发展过程。图8绘制了在不同荷载下，应变在截面上的变化。因UHPC梁顶与桥面板相连，无法设置测点，故图中用板底靠近梁上翼缘边缘的测点16和17代替。图中应变值为梁两侧测点数据的平均值。从图中可以看出，直至加载至240 kN，截面上应变分布与平截面假定吻合较好，中和轴位于距梁底约490 mm的高度范围；在加载至300 kN后，由于梁底拉应力增大，初始微裂缝开展，梁下翼缘侧边应变陡然增大，中和轴高度明显上移，移动距离25 mm左右，但在整个试验过程中，中和轴始终位于UHPC梁内，未进入桥面板。

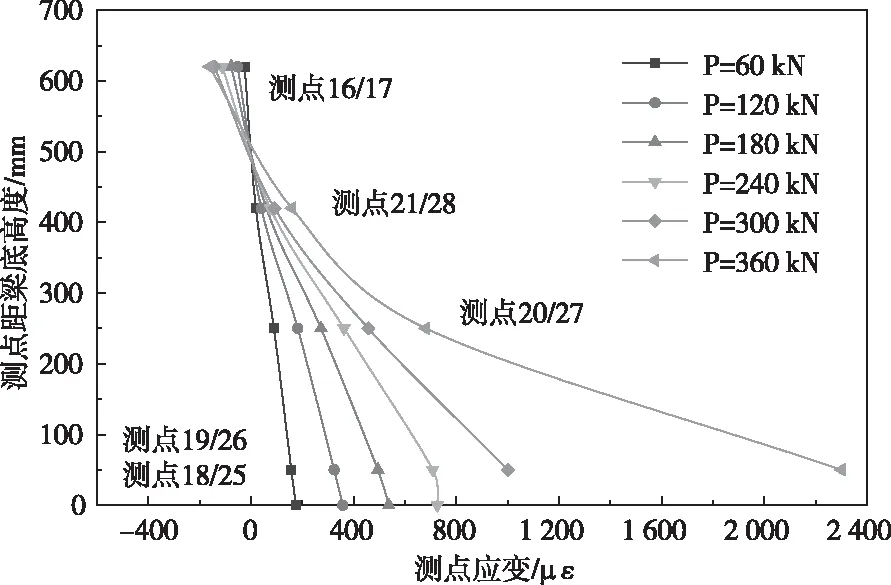
图8 UHPC工字梁跨中截面应变沿高度分布

2.4.3C50混凝土板两侧应变

桥面板两侧应变平均值分布见图9所示，由图可知，在整个加载过程，桥面板始终位于受压区内，由于中和轴位置相对来说在截面较高处，所有桥面板两侧应变值均相对较小。应变随着荷载增加而增长，在荷载达到300 kN后，上缘测点24、31和板中间测点23、30应变曲线斜率略有降低，中间测点也有所降低，但不明显，下缘测点22和测点29则一直保持较低应变水平，在荷载达到400 kN左右时，甚至有出现反向拐点的趋势。这是因为UHPC 梁底部裂缝发展，导致中和轴上升，受压区高度减小。

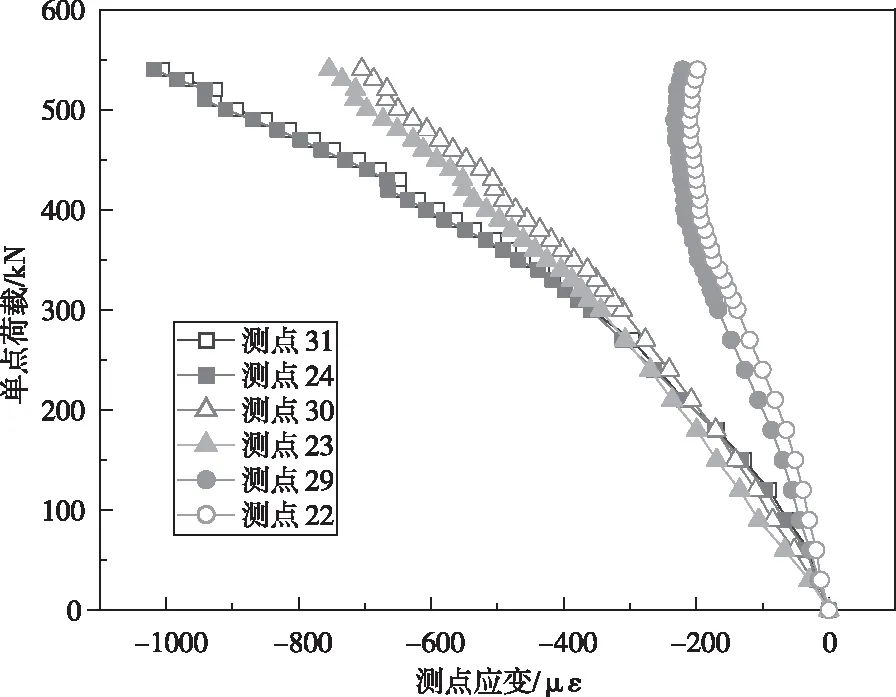
图9 桥面板两侧应变

3 有限元数值分析

采用ABAQUS有限元软件对试验梁进行受力过程的模拟分析，忽略UHPC工字梁与C50桥面板之间的滑移，以及钢绞线和灌浆料之间的滑移。

3.1 几何模型

UHPC梁、C50现浇板以及钢垫块采用八节点减缩积分单元(C3D8R)进行模拟，顶板内钢筋网、预埋件以及工字梁内预应力筋采用2节点线性三维桁架单元(T3D2)进行模拟，模型网格尺寸为5 cm×5 cm，模型如图10所示。

图10 试验梁有限元模型

3.2 材料本构

试验梁有UHPC、C50普通混凝土、钢绞线以及HRB400钢筋(顶板预埋件以及钢筋网)四种材料，混凝土选取ABAQUS提供的损伤塑性模型进行模拟。

3.2.1C50混凝土应力-应变关系

C50混凝土的应力-应变关系根据我国《混凝土结构设计规范》(GB50010—2010)[17]中对普通混凝土本构的相关描述计算所得。而针对ABAQUS中混凝土损伤塑性(concrete damage plasticity，CDP)模型所要求输入的受压损伤因子Dc-非弹性应变、受拉损伤因子Dt-开裂应变，则可以根据能量等效假设进行计算，即：

(1)

式中，dc、dt分别为混凝土的单轴抗压、抗拉损伤演化参数，可根据《混凝土结构设计规范》(GB50010—2010)计算所得。

3.2.2UHPC应力应变关系

UHPC材料根据文献 [18]，采用受压本构是简化后的CDP模型，即：

(2)

式中，σ为压应力，MPa；fc为UHPC抗压强度,MPa；x=ε/ε0，ε为压应变，ε0为受压应力峰值点对应的应变；上升段公式参数a的取值范围为1.0≤a≤1.2，本模型取值为1.0；下降段公式参数b的取值范围为2.0≤b≤5.0，本模型取值为5.0。

对于UHPC的受拉塑性取为理想弹塑性，本模型中极限拉应力取为8 MPa。

3.2.3钢绞线、钢筋的本构关系

模型中钢绞线采用双折线曲线，HRB400采用理想弹塑性模型，其中钢绞线屈服强度为1 760 MPa，极限强度采用设计标准强度，为1 860 MPa；HRB400钢筋屈服强度取抗拉标准强度，为400 MPa。

3.3 数值分析与试验值的对比

3.3.1荷载-位移曲线

由图11可知，试验值和模拟值整体上比较吻合，发展趋势大体一致，说明本文采用的有限元模型能较好地模拟无筋预应力UHPC组合梁的受力过程。试件开裂以前，有限元计算值和试验值基本相同；开裂后，有限元计算值比试验值略大，原因一方面是有限元模型中预应力筋以及普通钢筋与混凝土之间采用了嵌入连接形式，未考虑黏结-滑移问题；另一方面是模型中UHPC采用了简化后的的CDP模型，难以准确模拟开裂后的损伤情况。

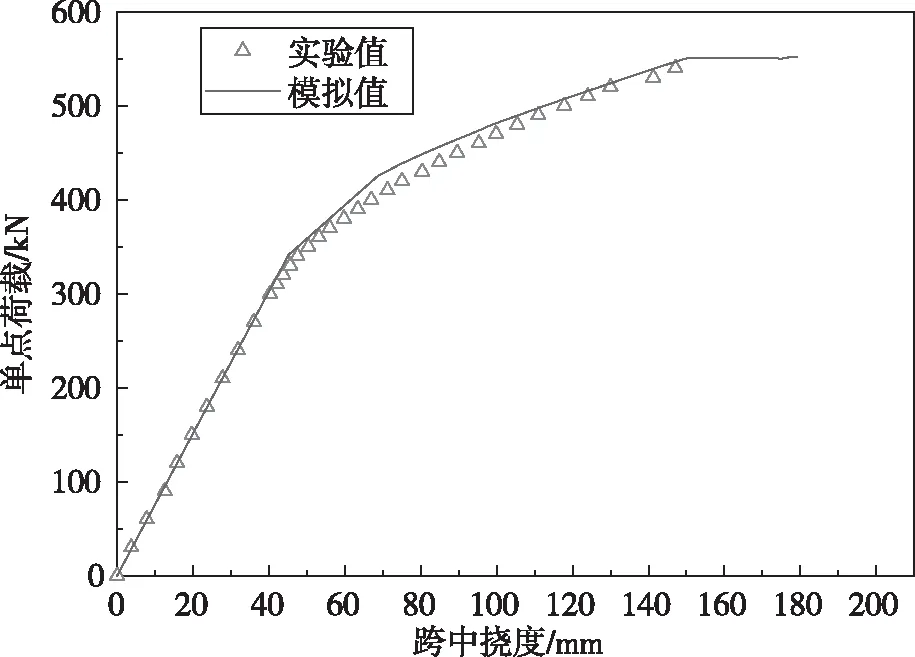
图11 荷载-位移曲线有限元模拟和试验值对比

3.3.2应变对比

图12为模型跨中纯弯段梁顶、底板的荷载-应变关系模拟值与实测值对比图。由图12可知，梁的顶板一直处于受压状态，其中在荷载达到300 kN之前，应变处于线性上升阶段，之后为非线性上升阶段，模拟值与实测值几乎重合。梁底在未开裂前各测点的应变值呈现线性增长，各个测点的应变值与有限元计算值吻合较好；梁底开裂后相应测点的应变值依次进入非线性增长阶段，应变不再均匀分布，有些测点位置处有裂缝的产生，应变急剧增大，如测点9和25，测点8的应变片由于裂缝开展损坏，梁底测点3的应变与计算值吻合较好，该处没有出现裂缝。

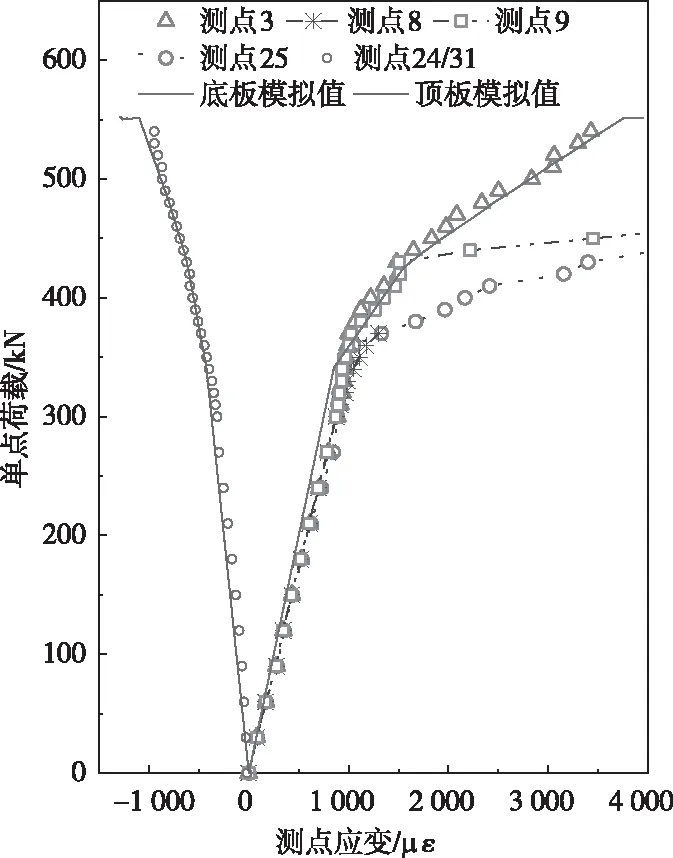
图12 跨中纯弯段顶板、底板应变计算值和实测值对比

通过以上梁顶板受压区混凝土的压应变、梁底拉应变的实验值和有限元计算值的对比表明，采用本文提出的有限元计算方法，可以有效地对该试验梁进行受力模拟计算。

4 结论

依托广州北环高速扩建F匝道桥，开展了16 m无筋预应力UHPC工字梁足尺模型的抗弯试验研究，分析了荷载、位移、裂缝发展以及应变，并与非线性有限元分析结果进行对比，得到以下结论：

(1)UHPC梁的抗裂性能大大提高，UHPC梁底拉应变达到785 με后，才出现开裂；和钢筋混凝土梁相比，裂缝分布细而密，宽度不大。

(2)无筋预应力UHPC工字梁跨中截面混凝土的平均应变与梁高之间呈正比例关系，符合平截面假定。

(3)无筋预应力UHPC工字梁与普通混凝土桥面板之间界面滑移量极小，现浇板与UHPC梁之间连接良好；桥面板的存在有效的增大了受压区的高度，对增大UHPC工字梁抗弯承载力起到了重要的作用；

(4)UHPC组合梁抗弯承载力满足设计要求，在弹性段应力水平与变形性能与设计结果吻合良好；进入弹塑性段后承载能力仍有较大发挥空间。

(5)采用有限元模型对UHPC组合梁进行受力仿真分析，弹性模型在梁开裂前，荷载和变形与试验值十分吻合，开裂后，弹性模型的挠度计算值比试验值大；采用CDP模型模拟UHPC的非线性以及桥面板普通混凝土的损伤进行仿真分析，试验梁开裂前和开裂后挠度和应变的有限元计算值与实测值吻合较好。