一种干涉仪测向解模糊的方法
2021-06-16吴自新李钊刘涛
吴自新 李钊 刘涛
(中国电子科技集团公司第二十九研究所 四川省成都市 610036)
对辐射源的高精度测向是实现电子支援态势感知能力的基础关键技术,对电子支援系统[1]具有非常重要的意义。干涉仪测向技术可实现单脉冲测向[2],能实现工作空域、频带瞬时宽开[3],并具有测向精度高、结构简单、原理清晰等优点,是实现对辐射源高精度测向优选技术体制,在现代电子支援系统中获得了广泛应用。如美军F-22 飞机AN/ALR -94 无源探测定位系统和F-35 飞机AN/ASQ-239 电子战系统均采用了干涉仪测向[4]技术体制。为满足电子支援瞬时超宽工作频带和宽空域测向要求,为实现高精度测向,在工程应用中大多采用多基线相位[5]干涉仪阵列,利用短基线保证较大的测向范围,长基线保证较高的测向精度。然而干涉仪测量相位存在整数周期相位差模糊,在解相位模糊[6]处理时涉及到解相位模糊的正确概率。如何高效的解模糊存为多基线相位干涉仪测向的关键问题,一般运用长短基线逐级解模糊[7]、虚拟基线解模糊[8]、基于余数定理解模糊[9]等方法,本文在此基础上提出了一种高概率的解模糊算法,具有解算正确率高、鲁棒性好、相位误差影响小的优点,较好地解决了多基线相位干涉仪测向工程应用问题。
1 干涉仪测向的模型及原理
干涉仪测向是通过测量辐射源到达接收天线口面之间的相位差来确定辐射源的入射方位。多通道相位干涉仪测向示意图如图1 所示。假设辐射源入射方位与干涉仪天线阵列轴线夹角为θ,干涉仪天线阵列间的基线长度为d1、d2、…dn-1,辐射源信号波长为λ,则辐射源信号到达基线长度为di的两个接收天线口面的相位差 为:


式(2)中 为测量相位差,ki为模糊数,有多值存在的可能性,正是由于ki的多值性才难以确定来波的真正方向,因而产生了测向模糊问题。
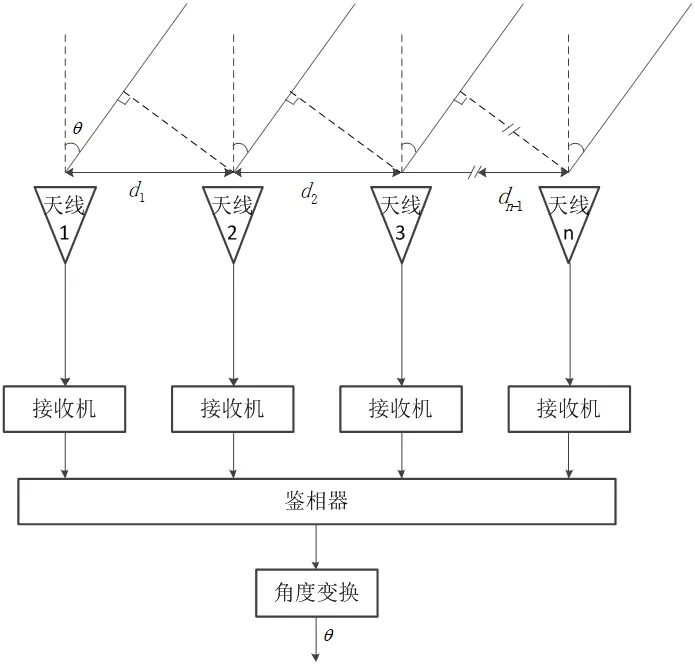
图1:多通道相位干涉仪测向示意图
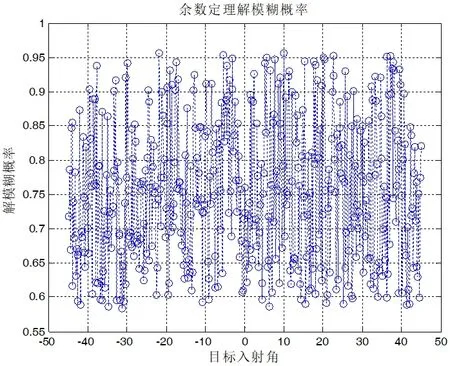
图2:余数定理法解模糊概率
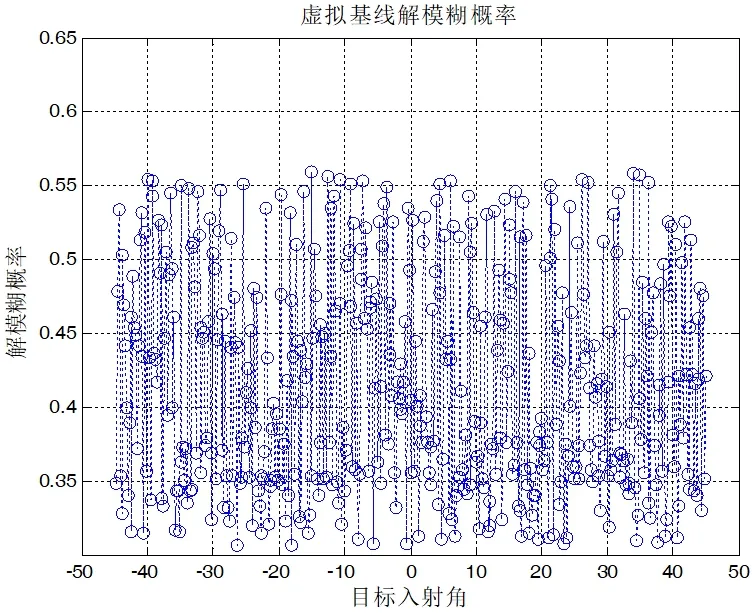
图3:虚拟基线法解模糊概率
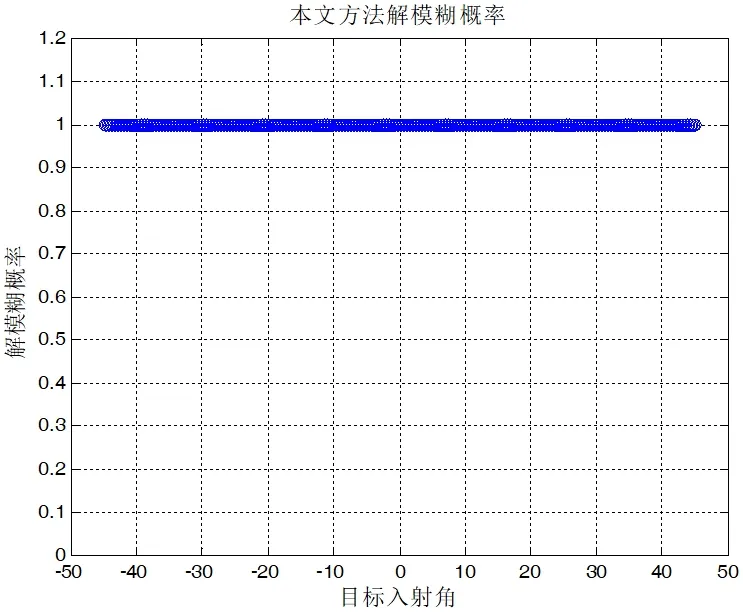
图4:多通道相位干涉仪测向示意图
通过鉴相器测出相位差 后,就可通过角度变换得到辐射源入射角θ:需要重点研究的问题。因此,如何解模糊或能否解模糊成为提高干涉仪测向精度的关键所在。
2 传统干涉仪测向解模糊方法
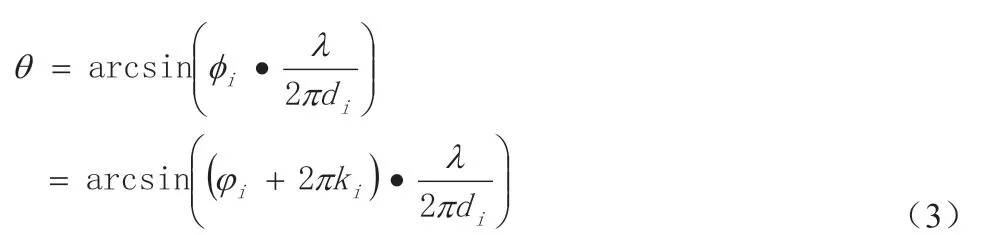
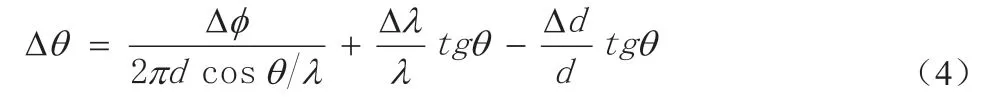

目前多基线相位干涉仪解模糊技术的基本方法主要有:长短基线法、余数定理法、虚拟基线法、无模糊长基线干涉仪法等,基本思想都是找出多基线相位干涉仪阵列中阵元基线长度的线性组合,使其满足小于辐射信号半波长的条件。
2.1 长短基线法
长短基线法是利用短基线保证测向输出无模糊值,长基线保证测向精度,该法的关键在于选择合理的长基线与短基线的比值。长短基线法要求短基线长度小于辐射源信号波长半个波长λ/2,在现代电子支援系统中高波段目标信号波长一般不大于20mm ~30mm,小于其半波长间距的基线通常难以直接物理实现,且基线较短时天线阵元间存在互耦影响相位差,因此长短基线法一般不适用。
2.2 余数定理法
在多基线相位干涉仪中设计采用参差基线,可以巧妙地解决天线阵列工程化问题,其理论依据是中国余数定理,基本要求是天线阵元基线长度满足互质关系。

式(6)为一个除数为整数的实数域内的同余方程组。若选择di两两互质,根据余数定理,式(6)存在唯一解。在工程实际中,由于测量相位差 会存在误差,解模糊的过程实际上是在M 个天线阵元基线中,求解一组ki使得最小。
理论上,测量的剩余数是非常准确的整数,然而在工程实际中鉴相误差[10]的存在,导致剩余数存在误差。如果有一个余数测量存有偏差,将会导致测向错误,存在测向跳区现象。另外,余数定理要求基线长度互质,在宽频带电子支援系统应用中,要求互质的参差数大,天线阵列形式单一,基线的位置误差可能会导致基线长度难以满足参差关系。
2.3 虚拟基线法
虚拟基线解模糊方法是选取两组基线长度相减,构造出一个短基线,使得该基线长度满足小于辐射源信号波长半个波长λ/2。在此基础上利用所构造的短基线测向结果依次解较长基线测向模糊,达到保证测向精度的目的。虚拟基线法可以很好的解决工程实际中存在的短基线长度不能过短的限制,极大的扩展了测向使用的频段范围。
虚拟基线法在理想情况下,只要选取的基线长度满足虚拟基线长度的要求就能实现测向解模糊,但是在工程实际中,受鉴相误差的影响,采用虚拟基线法仍然存在一定概率错误解模糊。
虚拟基线相位差是由两个基线的相位差相减得到的,因此虚拟基线相位差的均方误差是实基线均方误差的倍。另外,虚拟基线di一般较小,由式(5)可知其测角误差大。而虚拟基线能够正确解模糊的条件为:

3 高概率的干涉仪解模糊方法
该方法为降低鉴相误差的对解模糊的影响,首先通过卡尔曼滤波减小同频点目标信号相位噪声;再根据各基线滤波后的鉴相相位差求取理论上可能的全部入射角,参考各基线无模糊区进行分别进行角度分组;由于目标信号实际入射角是唯一的,故可取最大概率分布的角度作为入射角求解值。
卡尔曼滤波是系统状态的最优估计,以使系统状态估计值的均方误差最小,其主要是通过数学递推实现的。对相位差采用卡尔曼滤波,包括了两个过程即预测过程和校正过程。预测过程是系统状态方程通过系统上一历元的状态估计值对当前历元状态进行预测估计的过程。校正过程则是通过实际的测量值来对上一步预测得到的状态先验估计向量进行校正的过程。在校正过程中,因为实际测量值对状态估计向量进行了验证,所以状态估计向量的均方误差得到减小,可靠性也得到增加。鉴相相位差的状态方程和测量方程为:

式(8)中状态向量x 为鉴相相位差真实值,输出的测量值y为实测值,w 表示鉴相相位差变化率的二阶导数对鉴相相位差的影响,A、B 是由鉴相相位差关于初值、变化率、变化率的导数等的函数中系数构成,C 为1 行3 列的向量,v 表示鉴相过程中的测量噪声。
该方法的解模糊原理图与图1 相同,首先求得各基线的模糊数ki,在此基础上利用滤波后的相位差 ,遍历模糊数kj=[-ki:1:ki],求取全部可能的入射角θij。在此基础上参考各基线无模糊区θiu进行分别进行角度分组,取最大概率分布的角度作为求解值。
4 数字实验及分析
为验证上述干涉仪解模糊方法的性能,本文采用蒙特卡罗统计模拟法进行了仿真实验开展对比验证,重点对比余数定理法解模糊概率、虚拟基线法解模糊概率和本文提出的方法解模糊概率。仿真实验的主要参数:基线长度分别为95mm、85mm、115mm 的三基线干涉仪各基线鉴相相位差服从均值为0,均方差为40°的高斯分布,目标信号入射角θ ≤45°,频率12GHz,角度步进值为0.2°。仿真三种算法的解模糊性能时,对每点进行10000 点的蒙特卡罗仿真,统计解模糊概率。
图2、图3、图4 是三种方法的解模糊概率仿真情况,从仿真实验中可以看出,在实验条件下余数定理法解模糊概率相对于虚拟基线法解模糊概率成功率较高,本文提出的解模糊方法可以100%完成解模糊;但本文的方法基于卡尔曼滤波和多基线最大概率统计,算法运算量较大,且对实时性高的应用会造成一定影响。
5 结论和评述
本文介绍了一种高概率的干涉仪测向解模糊算法,在简述干涉仪测向的模型及原理基础上,介绍了传统的干涉仪测向解模糊方法,给出了高概率的干涉仪测向解模糊方法原理,并采用蒙特卡罗统计模拟法开展了仿真对比验证。验证结果表明,该方法解模糊概率明显优于传统方法。
