双频隔振系统隔振性能参数影响性研究

刘晨，冯志壮，邢龙涛

（中国直升机设计研究所直升机旋翼动力学重点实验室，江西景德镇，333001）

直升机自1939年问世以来，因其垂直起降、灵活机动和低空低速特性，在抢险救援、侦查勘测和人员物资运输等领域发挥着无可替代的作用。随着新型旋翼机更大前飞速度、更高效率和更远航程的发展需求，出现了倾转式、复合式、停转式等新式高速机型。但因受飞行状态和机体结构的影响，新型直升机易出现更大的振动问题，将对驾乘者和设备仪器带来严重影响。因此，直升机减振技术一直是设计研究中的关键[1]。

与常规直升机相比，共轴高速直升机在高速、高机动飞行状态下，旋翼振动载荷和机体振动水平远高于常规机型。为避免高速前飞时前行桨叶激波失速，需降低旋翼转速，这样必然会改变振动载荷的频率，从而改变机体振动响应的频率[2]。以如图1所示的美国SB＞1“挑战者”直升机为例，悬停状态时，其旋翼转速Ω为446 rpm；而高速前飞状态时，其旋翼转速Ω下降至360 rpm，此时直升机的振动主要有NΩ1和NΩ2（N为桨叶数）两个频率值。

主减结构是旋翼激振力传向机体的主要传递通道，通过安装弹性装置能够减小振动载荷的传递率[3]，如图1所示。上世纪60年代，Flannelly[4]提出了动力反共振理论(Dynamic Antivibration Isolator，DAVI)，DAVI系统能有效降低直升机的振动水平。随后，欧直的研究者[5]将DAVI与聚焦式柔性圆盘结合形成了SARIB 隔振系统如图3所示，该系统兼顾了垂向和旋翼平面内振动载荷的隔振性能。在国内，顾仲权等[6]提出了采用弹性轴承支撑结构的DAVI隔振器。黄传跃等[7]提出了一种兼具柔性隔振和反共振隔振的新型隔振装置，在该装置中利用联合梁式结构替代了原有弹簧式结构。邓旭东[8]提出了一种采用橡胶弹性扭管的新型隔振系统，并研究了各参数对隔振性能的影响性。随着控制技术的发展，主动式隔振逐渐应用于直升机中[9]。主动式隔振通过自主调谐质量、刚度等，达到针对目标频率的振动控制[10]；或通过作动器施加主动控制力，与外激力相互抵消达到隔振目的。主动隔振的效果明显，控制范围广，但对控制方法和空间要求高，同时其稳定性依赖于控制算法，容易发散而导致系统失效[11]。目前为止，已有多种振动控制措施应用于直升机的隔振设计。但在高速直升机振动预测及减振设计方面，还缺少系统的分析方法和相关的试验研究。

图1 直升机主减隔振系统结构

本文针对新型直升机的振动问题，从隔振原理出发，推导了双频隔振系统的动力学模型，对模型中的设计参数对系统隔振性能的影响性进行了研究，给出了双频隔振系统的两个隔振频率与各参数的关系。针对现有动力反共振隔振反共振区域频率范围窄、新型高速直升机转速可变的特点，为相关直升机主减隔振系统的设计提供理论参考。

1 双频隔振系统理论推导

在单频DAVI的基础上，在配重质量相连的杠杆上添加一套弹簧质量，可使隔振系统增加一个位移自由度，得到双频隔振系统（双频DAVI），从而在原有单一反共振频率点的基础上获得另一个反共振频率点，其理论模型如图2所示。在该模型中，mp为上端质量（旋翼部分），mf为下端质量（机体部分），mt为主配重质量，m2为附加配重质量，up、uf、ut和u2分别是上端质量、下端质量、主配重质量和附加配重质量的位移（以向上为正），k1为上下质量之间相连的主弹簧刚度，k2为附加配重质量的附件弹簧刚度，a为上下质量支点之间的距离，b为主配重质量mt至下端质量支点之间的距离。

针对双频隔振系统，由杠杆运动的协调性及传统动力反共振原理可知，系统中各质量的位移关系如下：

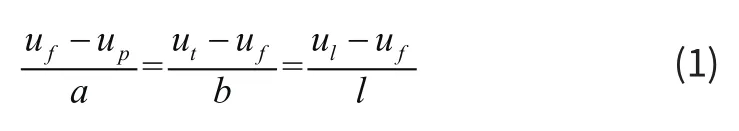
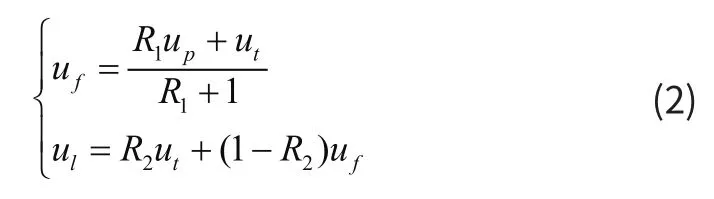
对于如图2所示系统，忽略杠杆、弹簧的质量，则该系统的总动能T和势能V表达式如下：

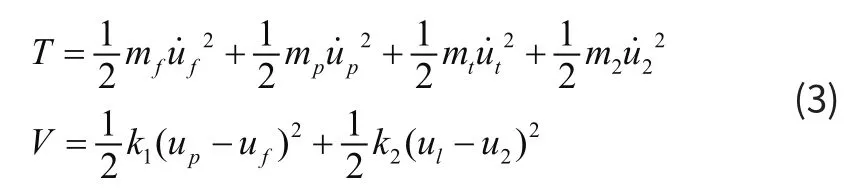
将uf和ul的表达式（3）代入上式可得：

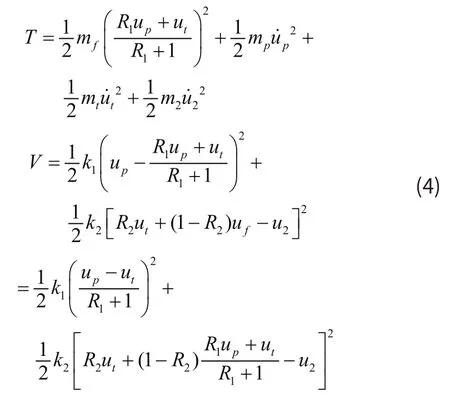
根据Lagrange方程：

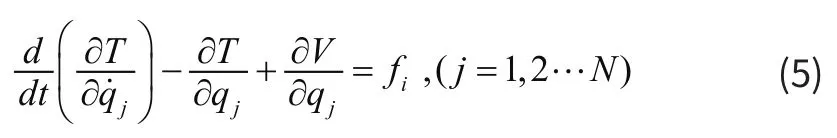
可建立该系统的振动微分方程如下：

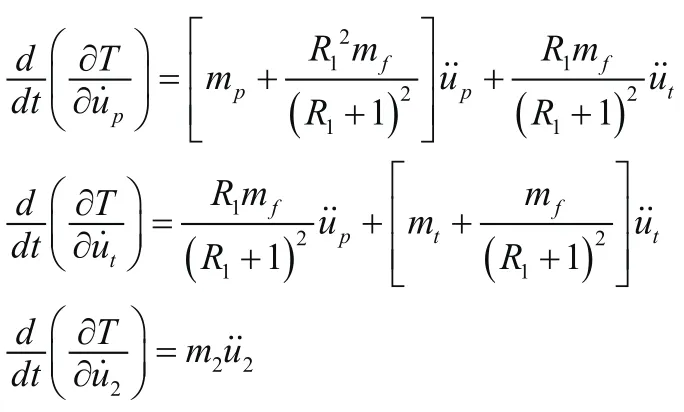
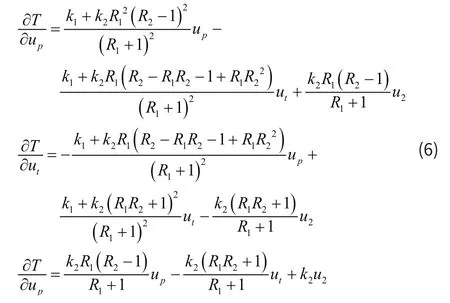
将上述表达式(6)代入Lagrange方程，可得到方程组的矩阵形式如式(7)所示：

则该系统的固有频率可表示为：

其中，K为整体刚度矩阵，M为质量矩阵。

通过求解该方程可得到该系统的固有频率，此时行列式会出现频率的6次方，即ωn6，化简后为ωn4，因此含有两个固有频率。提取各项的系数如下：

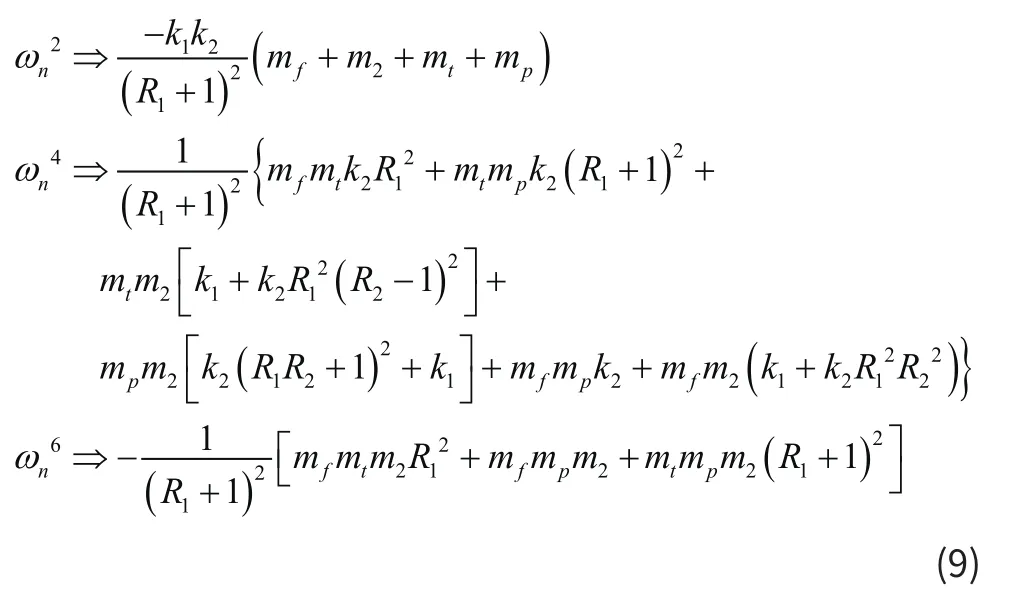
同时可以得到频响函数H(ω)：

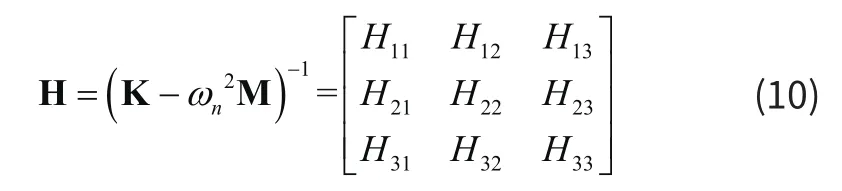
由杠杆原理可知，当质量mf的位移uf为0，则有：

此时的频率值为该隔振系统的最佳隔振频率。进一步可得到该双频隔振系统的位移传递率表达式如下：

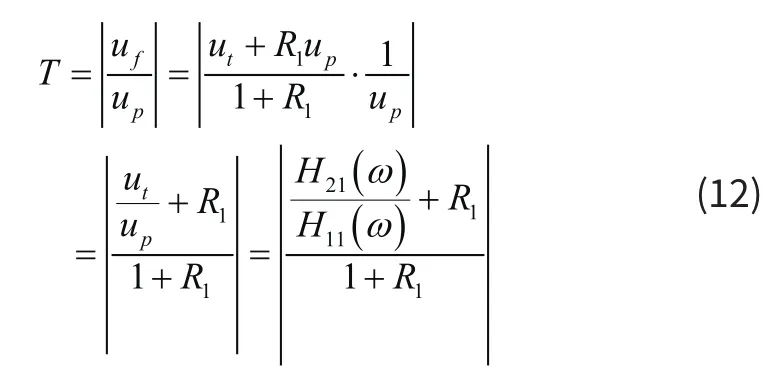
2 模型验证

为验证本文数值计算模型的准确性，利用有限元对计算模型进行动力学分析，对双频隔振系统的传递率进行对比。相关的参数定义为：k1=88339 N/m，k2=15175 N/m，a=0.1 m，b=0.4 m，l=0.15 m，mf=9.28kg，mp=4.51 kg，mt=1.23 kg，m2=1.06 kg。计算中采用弹簧单元对弹簧刚度进行等效，计算所得传递率对比结果如图3所示。

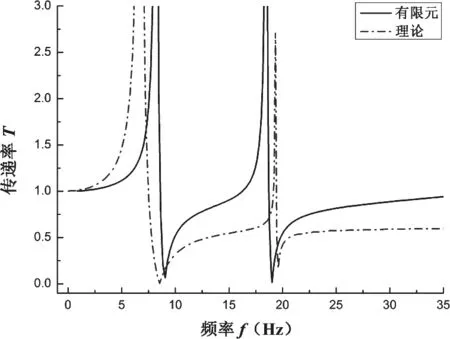
图3 双频隔振系统传递率对比

通过计算可得到双频隔振系统的两个最佳隔振频率，第一隔振频率有限元结果为8.95 Hz，理论结果为8.52 Hz，误差为4.8%；第一隔振频率有限元结果为18.95 Hz，理论结果为19.54 Hz，误差为3.1%。相应传递率曲线存在些许误差，这是由于数值计算采用简化模型，忽略了部分结构的刚度及质量的影响，同时模型采用了小角度假设，忽略的杠杆运动角的影响，但两种方法计算所得到的隔振频率吻合程度较好，误差均在5%以内，表明了本文计算方法的有效性。

3 双频隔振影响性分析

为进一步探究双频隔振系统中各个设计参数对其隔振性能的影响性，下面对系统中可作为变量的参数进行分析。该系统中所包含的质量mp和mf分别代表直升机中旋翼部分的质量和机身部分的质量，因此作为固定参数，其他参数可作为研究变量。在讨论单一变量对系统隔振性能影响时，其他参数均以上一节中的取值。

■3.1 上下质量支点距离的影响

为研究上下质量支点距离a对隔振频率的影响，令长度比q1=a/b，通过改变变量a得到双频隔振频率与q1的关系如图4所示。由式(12)可知，上下质量支点距离主要影响R1，结果中隔振系统的第一和第二隔振频率随支点距离a增大而升高。第一隔振频率变化率逐渐减小，当q1＞0.7后，隔振频率的变化不明显；第二隔振频率变化率逐渐增大，当q1＞0.7后，两个隔振频率的间隔逐渐增大。

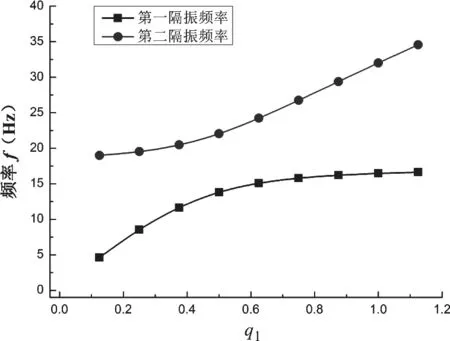
图4 上下质量支点距离对隔振频率的影响

■3.2 配重质量位置的影响

3.2.1 主配重质量位置的影响

从图2中可知，主配重质量mt距离支点的长度为b，从上一节理论推导过程可知长度比R1=b/a，通过改变长度b，可以得到双频隔振频率与R1的关系如图5所示。由结果可知，配重质量mt位置对第一隔振频率的影响较小，第一隔振频率随R1的增大而略有降低；配重质量mt位置对第二隔振频率的影响较大，尤其当R1＜2时，第二隔振频率显著减低；当R1＞2时，两个隔振频率的变化趋势相近，配重质量mt位置对隔振频率的影响效果不再显著。

3.2.2 附加弹簧质量k2-m2位置的影响

与单频DAVI相比，双频DAVI通过设计一套附加弹簧质量k2-m2，从而增加了一个反共振隔振点。为讨论附件弹簧质量的位置对系统隔振频率的影响，令长度比q2=l/a，通过改变附件弹簧质量到支点的长度l，可以得到双频隔振频率与q2的关系如图6所示。从图中可以发现，第一隔振频率随附加弹簧质量距离支点的长度l增大而均匀降低；而第二隔振频率随长度l增大而均匀升高，两个隔振频率的间隔逐渐增大。因此可通过调节附加弹簧质量k2-m2位置改变双频隔振频率的间隔。

图5 主配重质量位置对隔振频率的影响

图6 附加弹簧质量位置对隔振频率的影响

■3.3 弹簧刚度的影响

3.3.1 主弹簧刚度的影响

上下质量间相连的主弹簧刚度为k1，其对双频隔振系统影响如图7所示。从结果中可以发现，主弹簧刚度k1主要影响第一隔振频率，而对第二隔振频率的影响较小。第一隔振频率随主弹簧刚度k1的增大而升高，两个隔振频率的间隔逐渐缩小。通过调整主弹簧刚度k1，可针对第一隔振频率进行调节。

3.3.2 附加弹簧刚度的影响

与附加质量m2相连的附加弹簧的刚度为k2，双频隔振频率与附加弹簧刚度k2的关系如图8所示。从图中可以看出，当k2＞6000时，k2对第一隔振频率的影响性减小，第一隔振频率基本保持不变。而k2对第二隔振频率的影响效果较为显著，隔振频率随的k2增大而持续升高。因此调整附加弹簧刚度k2可对第二隔振频率进行针对性调节。

■3.4 配重质量的影响

3.4.1 主配重质量的影响

配重质量mt对双频隔振频率的影响如图9所示。由结果可知，当mt＜0.6时，配重质量mt对第二隔振频率的影响程度要大于对第一隔振频率的影响。第一和第二隔振频率随配重质量mt的增大而降低，而隔振频率间隔基本不变。

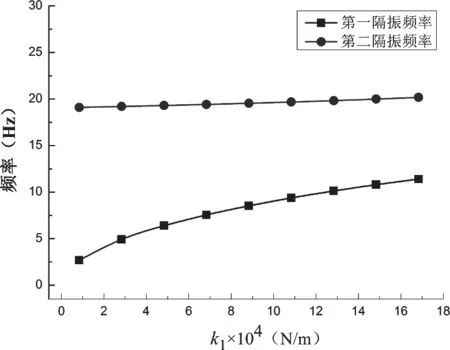
图7 主弹簧刚度对隔振频率的影响

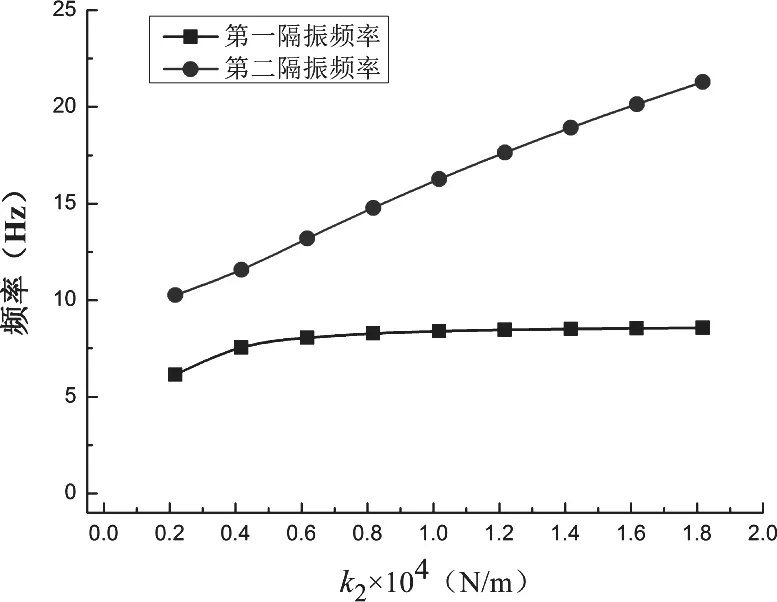
图8 附加弹簧刚度对隔振频率的影响

3.4.2 附加配重质量的影响

配重质量m2对双频隔振频率的影响如图10所示。从图中可以发现，第一隔振频率受配重质量m2的影响很小，第一隔振频率基本保持不变；第二隔振频率受配重质量m2的影响显著，隔振频率随配重质量m2的增大而降低，且变化率逐渐减小。因此在隔振器的设计中，可以通过改变配重质量m2来对第二隔振频率进行针对性调节。

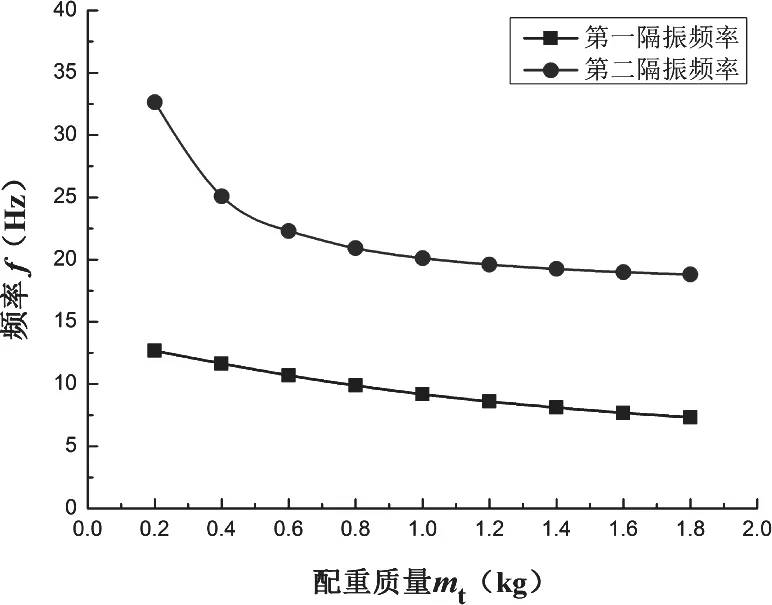
图9 主配重质量对隔振频率的影响

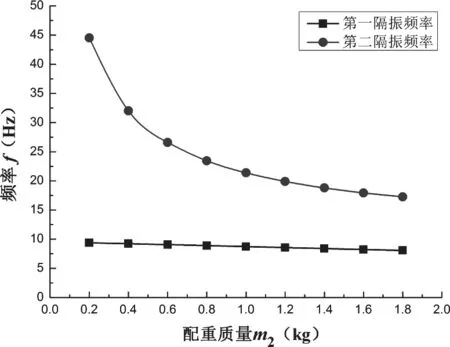
图10 附加配重质量对隔振频率的影响

4 结论

双频隔振系统通过在单频隔振系统中设计增加一组附加弹簧质量，使得在原有一个隔振点的基础上获得了另外一个隔振点。本文中推导了双频隔振系统的理论方程及传递率，并进一步探究了配重质量相关设计参数对隔振性能的变化规律，相关结论可整理如下：

（1）激励端与被隔振端质量连接于杠杆上的支点距离以及附加弹簧质量位置主要影响双频隔振频率的间隔。两个隔振频率随两个质量的支点距离的增大而增大，且两个隔振频率的间隔先减小而后增大。当q1=a/b取值在0.5附近时，两个隔振频率的间隔最小；随着附加弹簧质量距离支点的长度增大，隔振频率间隔增大，第一隔振频率逐渐降低而第二隔振频率逐渐升高。

（2）主配重质量的位置以及附加配重质量对第一隔振频率的影响较小，而对第二隔振频率的影响较为显著。隔振频率随主配重质量至支点的距离或附加配重质量的增加而降低。因此通过调整主配重质量的位置或附加配重质量可对第二隔振频率进行针对性调节。

（3）主弹簧的刚度主要影响第一隔振频率，而对第二隔振频率的影响较小；附加弹簧的刚度对第一隔振频率的影响较小，而对第二隔振频率的影响效果较为显著。隔振频率随主弹簧刚度和附加弹簧刚度的增大而升高。因此通过调整主弹簧刚度k1，可针对第一隔振频率进行调节；而通过调整附加弹簧的刚度可对第二隔振频率进行针对性调节。