基于FPGA的数字锁相放大器的设计

汤易，孙向阳

（电子科技大学电子科学与工程学院，四川成都，611731）

0 引言

在微弱信号的采集和处理中，锁相放大技术一直是一种行之有效的方法，该技术是利用相关的原理设计的一种同步相干检测，具有通频带窄，中心频率稳定，品质因数高，信噪比高等特点，在微弱信号的处理方面显示出了非常好的性能，因此在各个领域得到了广泛的应用。

1 锁相放大技术原理

在采集微弱信号的过程中，常常会有由电磁辐射或传输渠道等各种原因产生的噪声，设信号X(t)是伴有噪声的周期信号，即：

式(1)中X(t)为输入信号，由有用信号S(t)和随机噪声N(t)组成，有用信号的幅值为A，角频率为ω，相位为φ；参考正弦信号为：

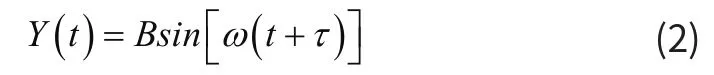
其中τ是参考正弦信号的相位，则两者的相关函数为：

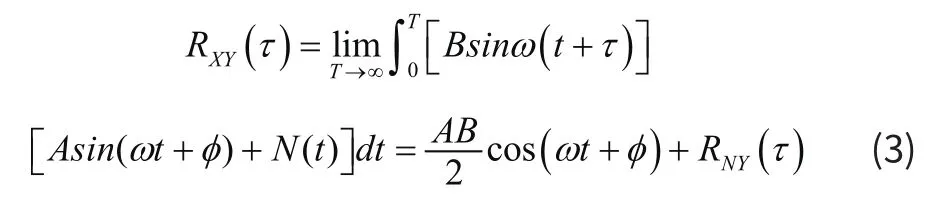
由于参考信号Y(t)与随机噪声N(t)互不相关，所以RNY(τ)=0 ，于是就有：

从而得出RXY(τ) 正比于有用信号的幅值的结论。

由以上分析可知，利用参考信号与有用信号相关的同时与噪声互不相关这一点，可以通过相关运算提高信噪比。

2 数字锁相放大器设计

本数字锁相放大器主要用于采集接收微弱信号系统中，整个系统主要分为两个部分：模拟部分和数字部分，数字部分基于FPGA开发，最终在硬件中进行实现，具体结构如图1所示。

图1 系统总体框图

图1中的FPGA模块即为数字锁相放大器部分，主要由移相器，相关检测，低通滤波和矢量运算等部分构成。在接收到前级AD模块的数字信号后，锁相放大器会将信号进行移相，移相后的数据和接收数据分别于参考信号进行乘法操作，经过低通滤波后，两路信号的比值反映了原始信号对应时刻的相位，而两者的模值反映了原始信号的幅度，从而实现了将小信号从噪声中提取出来的功能。

在整个数字部分中，功能主要在FPGA内实现，这需要考虑到硬件系统与理论上的不同。移相器主要参考工作频率，按照参考信号的频率将接收到的信号延迟半个周期，从而达到移相90°的功能；相关检测部分主要实现的是参考信号与接收信号的相乘，利用FPGA内自带的乘法器模块进行实现，以便满足时序与资源上的平衡；低通滤波器模块实现滤波，在硬件中实现需要大量的乘法器与加法器，考虑到芯片内部乘法器资源的有限性，这里采用了分布式算法，避免了乘法器的使用。

3 基于分布式算法的低通滤波器设计

■3.1 分布式算法原理

分布式算法由于用LUT和移位器代替乘法器，有效地节省了硬件资源，因此被广泛运用于FPGA的设计中，对于滤波器的计算：

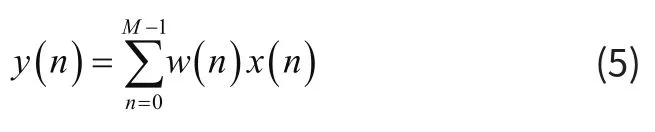
其中，x(n)可以表示为：

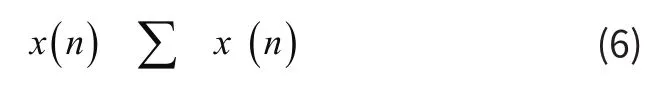
式(6)中，xb(n)代表x(n)的第b位，B为信号的位宽，所以有：

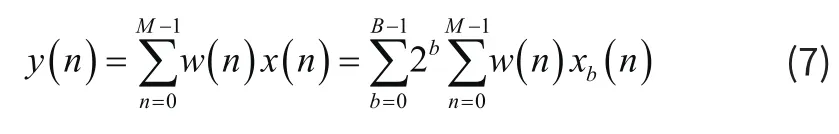
式(7)中M为滤波器长度，上式中的w(n)xb(n)中的xb(n)为输入信号的第b位，只有0和1两种状态，因此分布式算法将w(n)的所有累加组合预先存储在LUT中，通过对二进制位地址 [xb(0),xb(1), … ,xb(M－ 1 )]寻址提取对应系数组合，然后由移位器和加法器进行实现移位求和，从而变相实现乘法累加运算。

■3.2 基于分布式算法的数字滤波器

上述即为串行结构的分布式算法，基于分布式算法的数字滤波器结构框图如图2所示，由M位移位寄存器、LUT查找表和加减运算部分组成，LUT查找表的地址由每一个输入信号的同一位决定。

本文中我们采用FIR滤波器进行滤波，借助Matlab中滤波器设计工具fdatool进行设计。滤波器的参数如下：通带从5kHz到35kHz，滤波器的阶数为127阶。阻带容许最小衰减为50dB，根据这些设计指标，可以通过软件生成滤波器系数，同时绘制的幅频响应，幅频特性曲线如图3所示。

图2 数字滤波器结构框图

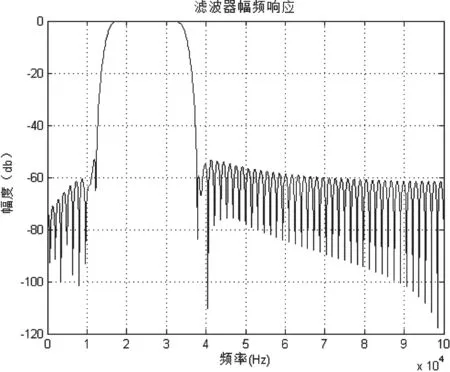
图3 理想幅频响应

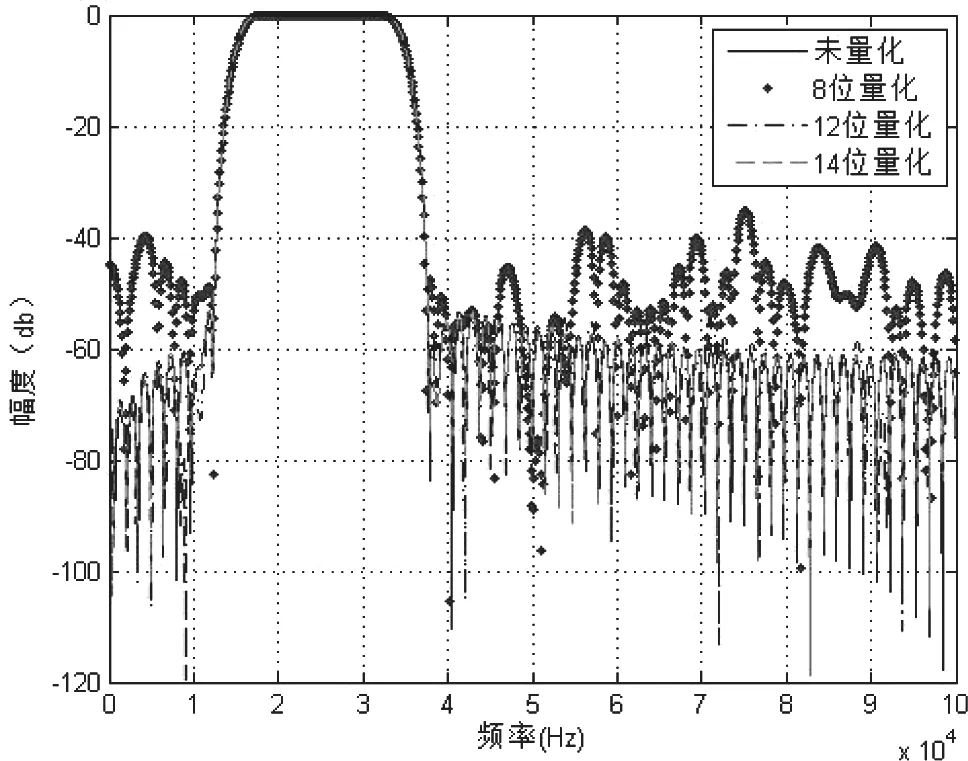
图4 不同位宽幅频响应对比

Matlab生成的滤波器系数均为浮点数，而FPGA中只能进行整型运算，因此需要对滤波器系数进行量化。滤波器系数的量化位数越大，滤波器的幅频响应与原始滤波器幅频响应拟合程度越好，但是需要消耗更多硬件资源；反之，滤波器系数量化位数越小，消耗硬件资源越少，但其滤波效果越差，因此需要平衡硬件资源的使用和精度的选择。我们选择了三种位宽，分别是14位，12位，8位，在Matlab中通过对比不同位宽下的幅频特性曲线与原始滤波器的幅频特性，选取最佳系数量化位宽。图4是不同位宽的幅频特性仿真图，从图4可以看出12bit与14bit位宽量化的幅频特性曲线和原本的幅频特性曲线拟合程度较好，而当采用8bit位宽量化时，幅频特性曲线失真较大。本着节约资源的想法我们选择12bit位宽量化。

最后我们将量化之后的系数导入FPGA中，通过分布式算法的思想完成整个数字滤波器，由于阶数较高，127阶共有64个不同的滤波器系数，若全部在一个LUT里查找需要存储264个数，因此本文将64个系数分成8组，每组系数中有8个，这样每个LUT只用存储28个数，在硬件资源上大大优化。数据每输入一次便会进行17次查找操作、16次移位操作以及1次加法运算，由于对数据进行了移位累加，因此数据的位数会被扩展，最后我们截取有效数据的高16位作为滤波结果。完成整个滤波器设计后我们在Modelsim进行仿真，将500Hz、20kHz、50kHz的三个正弦波叠加组合作为输入信号。结果如图5所示。

图5 数字滤波器仿真结果

从Modelsim仿真图中可以看出，输入信号中20kHz频率成分被保留了下来，而其他的频率成分均已被滤除，可见设计的滤波器基本满足设计要求。

4 数字锁相放大器仿真与测试

为了衡量锁相放大器提取信号幅度的效果，本文将正弦调制信号作为仿真的输入信号，其输入信号和测试结果如图6所示。

在图6中，adc_data端口即为仿真的输入信号端口，这是一个幅度调制信号，其幅度为一个正弦信号，图中的x_out端口即为输出信号端口，它代表数字锁相放大器中的幅度，可以看到，仿真结果基本符合理论结果，经过数字锁相放大器，提取了输入信号的幅度。

经过上述的仿真结果后，我们将程序下载进对应的FPGA开发板中，输入信号如图7所示。

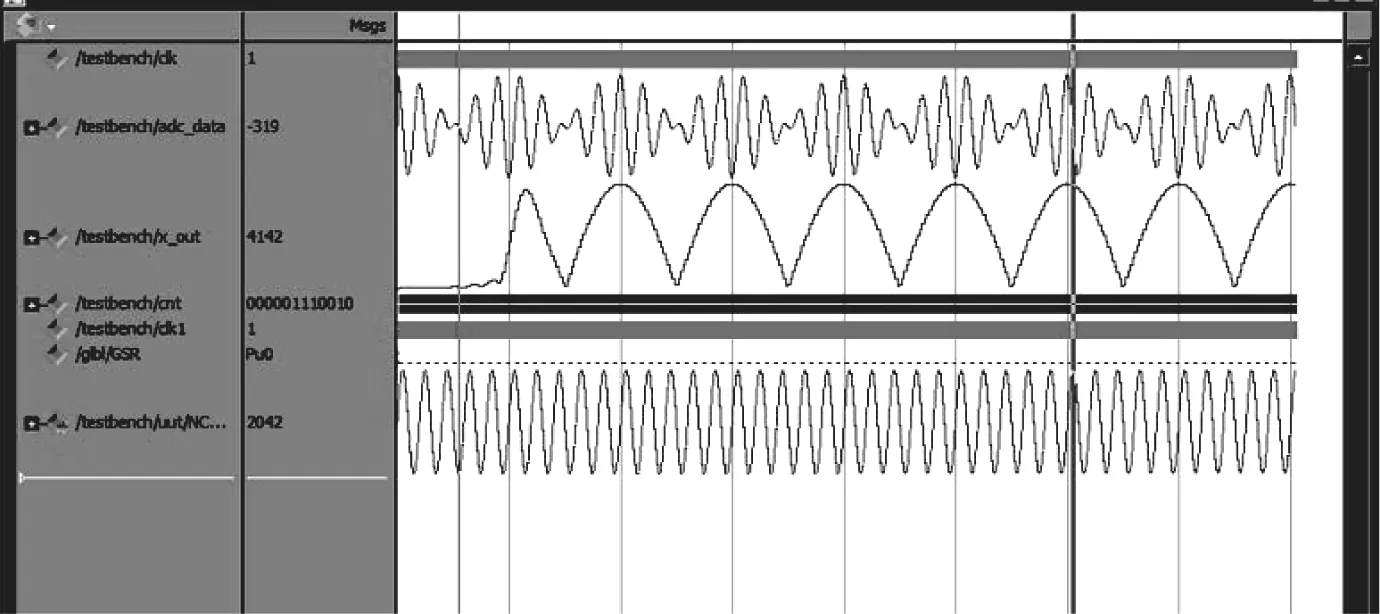
图6 数字锁相放大器仿真结果

输入信号由信号源产生，经过模数转换器后接在FPGA的输入端口，这里选择使用幅度为三角波的调制信号，得到的结果如图8所示。

图7 实际输入信号

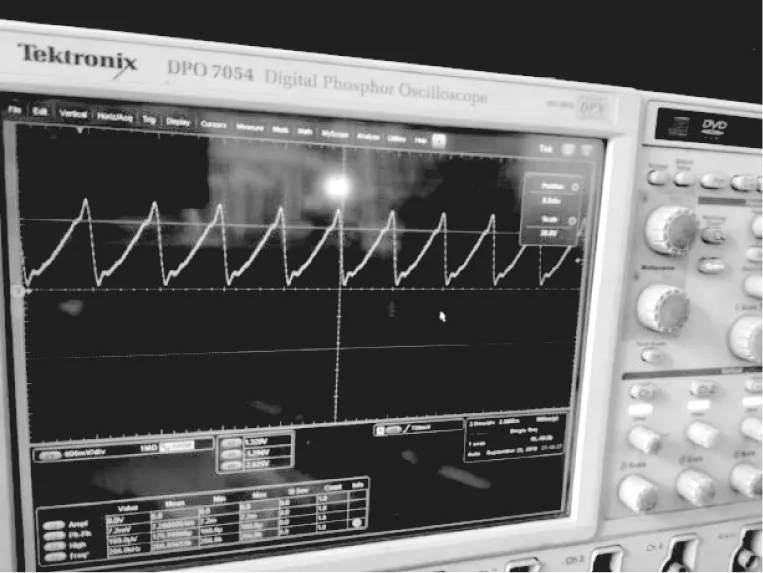
图8 示波器显示输出信号

通过示波器接收输出信号并显示，我们可以看到基本能完整的提取输入信号的三角波幅度，与理论和仿真结果差距较小。

5 结论

本文完成了一种数字锁相放大器的设计并分析了相关检测方法原理，完成了整体系统设计。通过上面的仿真和实际测试可以看到，数字锁相放大器的效果明显，实现后的结果与理论相比误差较小，能广泛运用于微弱信号检测中。