基于稳健估计方法的线性回归研究

王帅帅 徐凯 孟凡芳

摘  要：基于最小二乘方法的线性回归估计方法，是通过最小化误差平方和寻找参数向量最优解，该方法对大的误差点不具稳健性。本文主要针对具有异常点的稳健估计方法，研究在背景噪声下的稳健估计性能，并通过数值仿真证明近似高斯分布，如高斯混合噪声模型下，单调型稳健M估计方法较好;在具有无穷方差的柯西背景噪声下，回降型M估计性能最优。理论和仿真实验均可得到稳健回归方法比最小二乘方法具有更好的稳健性。

关键词：线性回归  最小二乘法  稳健估计  M估计  稳健性

中图分类号：O212.1                          文献标识码：A                  文章编号：1674-098X（2021）01（a）-0072-06

Abstract： Based on the least squares estimation method of linear regression aims to find the optimal solution of the parameters by minimizing the sum of squared errors， which is not robust to large error points. Here， we focus on the robust estimation with outliers， investigating the performance of the robust estimation under various background noise. We prove that the monotone M-estimator shows a better performance under Gaussian mixed noise and the redescending M-estimator has a better efficiency under Cauchy noise with infinite variance. Both theory and simulation experiments show that the robust regression method has better robustness than the least square method.

Key Words：Linear regression; Least squares method; Robust estimation; M-estimation; Robustness

线性回归模型是在实际工程建模中应用十分广泛的一类模型，例如无线通信、超声波系统、计算机识别、电力系统、生物医学信号分析等领域[1-3]。常用的估计回归系数的方法是最小二乘法（OLS）[4]。最小二乘估计最大的优点是对输入数据没有任何概率假设，要求偏差平方和最小。当数据服从高斯分布时，最小二乘估计是最优的估计。然而当数据中存在野值（又称异常值）时，这种估计方法的估计性能变差，因此最小二乘法是不稳健的。而真实观测数据中，异常数据是难以避免的。因此，研究线性模型的稳健估计方法很有必要，也具有实际意义[3]。

最小二乘估计与稳健估计方法的区别是，最小二乘估计赋予样本残差相同的权重，而稳健的估计方法的思想是赋予样本残差不同权重，残差大的样本赋予小的权重，残差小的样本赋予大的权重。相对于最优的估计方法，稳健估计损失了一定的效率，达到了很好的稳健性。本文通过分析在不同的背景误差噪声下，如高斯误差噪声，高斯混合噪声以及具有无穷方差的柯西噪声，稳健估计的性能与最小二乘回归的性能比较，并通过仿真模擬，证明在不同类型的背景噪声下，稳健估计回归方法比最小二乘方法具有更好的稳健性，在实际中能够得到更广泛的应用[3，5-8]。

1  线性回归模型

考虑线性回归模型

用矢量或者矩阵表示公式（1）为

求解回归系数的经典方法最小二乘法的思想是：使观测值yi与其拟合值之差的平方和最小，定义残差，也就是使得残差的平方和最小，即

当观测数据服从相互独立同分布的高斯分布时，最小二乘方法是一种最优的估计方法。从公式（5）可以看出，最小二乘估计是将所有的样本点赋予相同的权重，但是当观测数据中含异常值时，该方法的估计结果受异常值的影响大，而实际观测数据中有可能异常值是不可避免的，因此最小二乘估计稳健性差。常用的方法是异常值识别并剔除，但并没有一个客观的标准确定哪些是异常值，易受主观因素影响。另一种常用的策略是采用稳健的回归方法。稳健回归方法通过对不同的样本数据赋予不同的权重来减小异常值对回归带来的影响。加权最小二乘估计是一种比最小二乘估计稳健性强的估计方法，其原理是给每一个样本点赋予不同的权重，偏差较大的样本点给予小的权重，偏差小的样本点给予大的权重，而常用的一种稳健回归估计方法为M估计稳健回归，其基本思想是采用迭代加权最小二乘估计回归系数。本文以稳健M回归估计方法为基础，分析不同背景噪声下的稳健M估计的性能。

2  稳健回归分析

M估计稳健回归是对如下目标函数进行优化

其中W=diag（W1，W2，…，Wn）是n×n的对角阵。稳健M估计的方法是合理的，对于大的标准化残差ui，应该给予小的权重Wi，权重Wi与评价函数ψ的形状有关。对于背景噪声方差随时间变化时，加权矩阵取W=C-1=diag是合适的。因为越大，可信度越低，给的权重则应小。

稳健估计量不像最小二乘估计量有明确的表达式，通常采用迭代加权方法得到最终的估计量，具体的步骤：

（1）选取迭代初始估计值为L1估计量;

（2）对k=0，1，2，…，计算求得标准化残差和权重;

（3）利用公式（12）计算（k+1）;

（4）当时，停止迭代。

3  数值模拟

3.1 考虑一个直线回归模型

其中xi和yi分别是预测变量与响应变量，ei为随机误差。

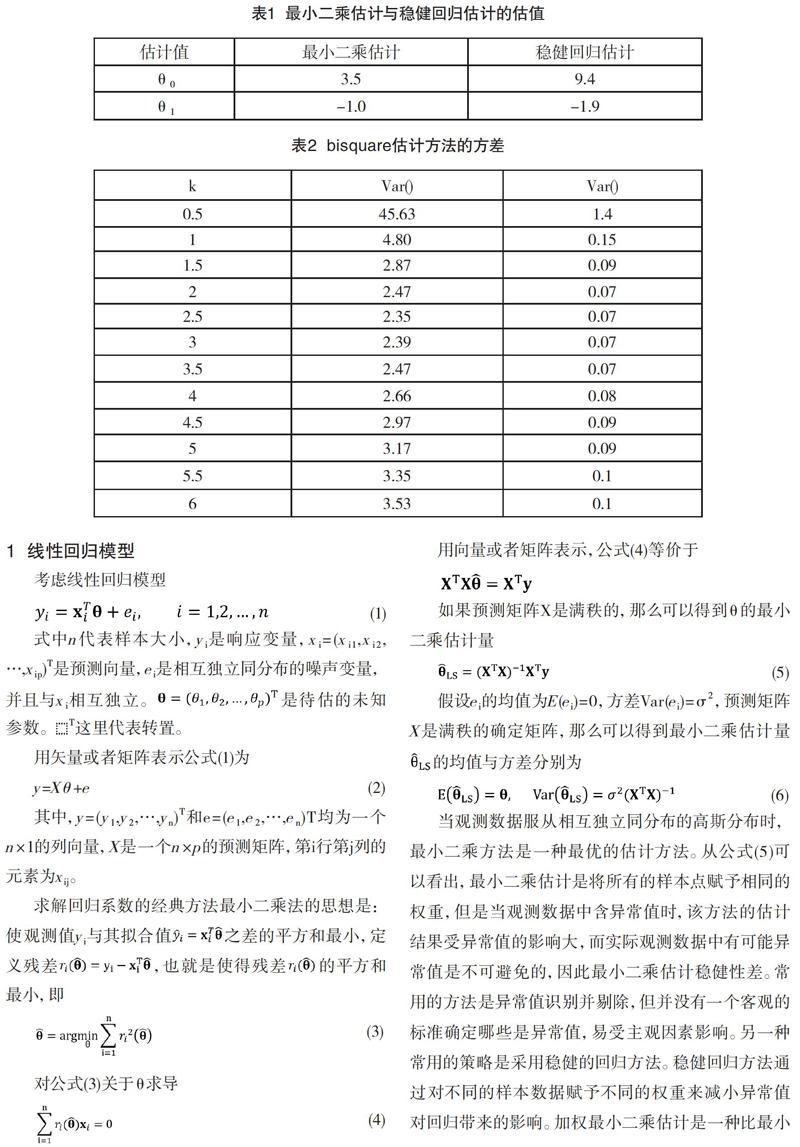
令θ0=10，θ1=-2，随机误差ei为标准高斯分布随机数，样本容量n=10，样本中含有两个异常点。我们分别采用最小二乘估计方法与稳健回归估计方法，得到的关于θ0和θ1的一次的估计值为表1所示。

通过作图，可以看出采用稳健回归的方法，拟合得到的直线更接近真实的直线，如图1所示。

3.2 不同背景噪声下的稳健回归特性

考虑公式（15）中的线性回归模型，真实直线的参数设置为θ0=0，θ1=-2，研究在高斯混合噪声以及厚尾柯西噪声下稳健M估计的性能。

在高斯混合噪声背景下，其概率密度函数为

其中。这里我们采用双高斯混合模型

采用最小二乘估计方法，得到估计量和的估值分别为9.97和-1.99，对应的估计量的方差分别为2.34和0.07。在混合高斯噪声下，采用最小二乘方法，得到了较好的估计性能;相同的条件下，采用参数k=0.8的huber估计量，可以得到的和的估值分别为9.99和-2.00，对应方差分别为2.21和0.06，可以看出稳健的huber估计方法的估计性能比最小二乘方法略微好一点，但相差不大。而此背景噪声下，公式（11）中回降型的bisquare估计量反而没能有较好的性能，其性能比最小二乘及huber估计量的性能略微差。

假设背景噪声是具有厚尾分布的柯西噪声，其概率密度函数为

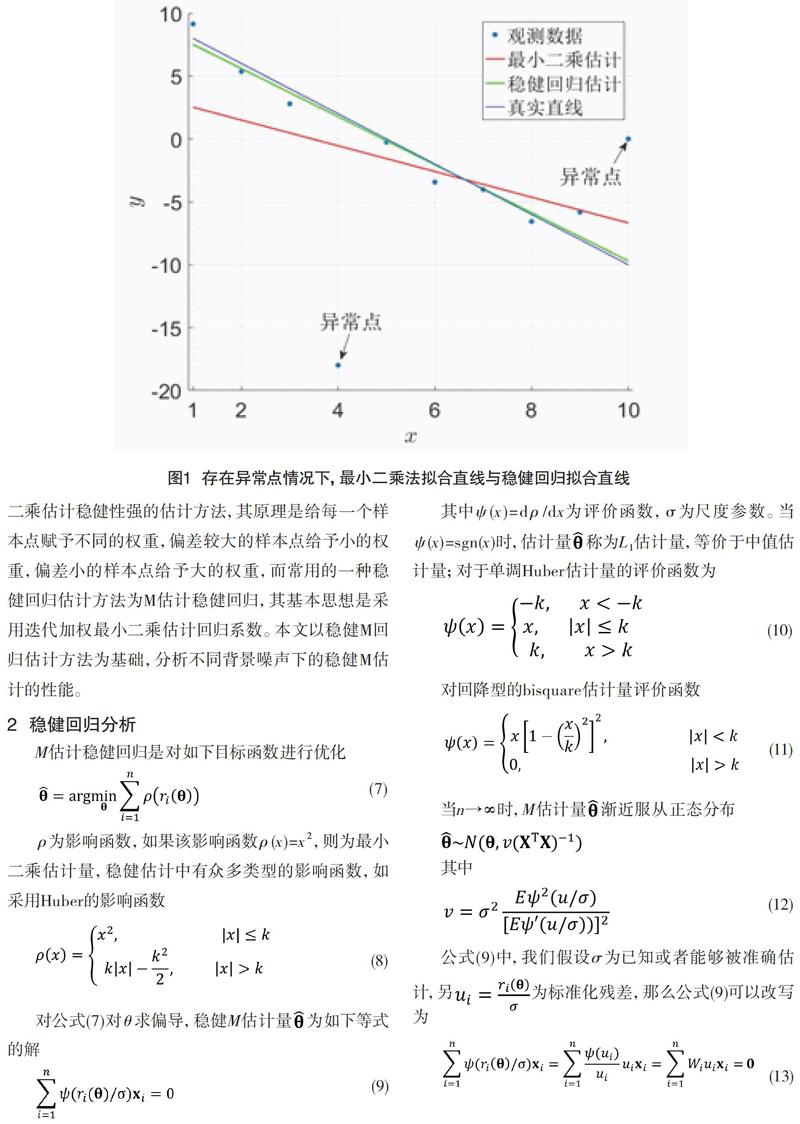
在此背景噪声下，我们分别采用公式（5）中的最小二乘估计方法，得到的估计量和的估值分别为7.18和-1.90，对应的估计量的方差分别为1.22×104和8.02×102，可见通过最小二乘方法得到的估计量的方差很大，性能较差;采用公式（11）的bisquare估计方法，计算得到不同估计参数k下，估计量和的方差在表2及图2中展示。由表2可以看出，对一定范围的估计量参数k，得到的估计性能均优于最小二乘方法的估计性能。由图2可以看出，当参数k选择一个特定的非零值，会使得估计量的方差达到最优，因此，可以通过调节参数k，寻求最优的估计量。

取使得估计量具有较小方差时对应的k=2.5，得到bisquare估计方法得到的和的估值分别为10.00和-2.00，做出bisquare估计方法拟合的直线与最小二乘方法拟合的直线的图形，如图3所示。从图3中可以明显看出，最小二乘方法拟合得到的直线偏离真实直线远，而通过bisquare方法得到的直线几乎和真实直线重合。

4  结语

本文基于稳健M回归估计方法，在高斯混合噪声模型及柯西噪声模型下，研究稳健估计方法的性能。对于高斯混合模型，稳健huber估计方法能够具有较好的估计性能，对于具有无穷方差的厚尾柯西噪声，采用回降型的bisquare估计方法得到的估计性能较好，无论采用何种方法，通过调节稳健估计量的参数，稳健回归估计方法都优于最小二乘法。

参考文献

[1] 畢瑞锋，张发玲.加权最小二乘法线性回归模型参数的理论推导与计算实例[J].计量与测试技术，2016，43（2）：67-68.

[2] 谷恒明，胡良平.简单线性回归分析及其应用[J].四川精神卫生， 2017（6）：494-497.

[3] Zoubir A M， Koivunen V， Chakhchoukh Y， et al. Robust estimation in signal processing： A tutorial-style treatment of fundamental concepts[J]. IEEE Signal Processing Magazine，2012，29（4）：61-80.

[4] 陈雨彤.基于最小二乘法的线性回归方程推导与应用分析[J].中国新通信，2018，20（24）：206-208.

[5] 吕晶.几类半参数回归模型的稳健估计与变量选择[D].重庆：重庆大学，2015.

[6] 傅可昂，丁丽，李君巧.重尾非线性自回归模型自加权M-估计的渐近分布[J].数学物理学报，2020，40（2）：475-483.

[7] 姜佃高，张娟娟，葛永慧.稳健估计方法在多元线性回归中的有效性研究[J].统计与决策，2014（18）：77-80.

[8] 刘晓芮，王清，陈植华，胡成.基于稳健回归-去趋势波动分析法的山前平原地下水转换关系研究[J].安全与环境工程，2019，26（5）：17-24.