平面直角坐标转换中一个问题的研究
2021-06-15刘延斌
刘延斌
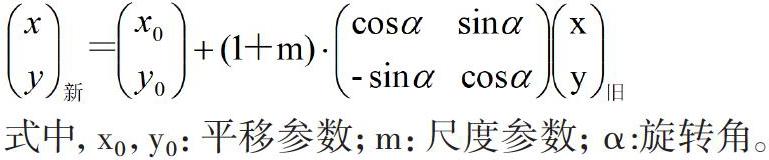

摘 要:通过实例演算,分析了定义坐标系的投影参数对平面直角坐标转换的影响。得知投影参数中,影响转换结果最重要的投影参数是中央子午线,而坐标系的其它投影参数的差异对转换结果的影响很小,则不必考虑。提出了在平面直角坐标转换中,只有两套坐标系的中央子午线相同时,才可直接进行转换,有差异时,会导致转换精度大幅降低,需分步进行转换,才能保证转换精度。
关键词:平面直角坐标 坐标转换 投影参数 中央子午线
中图分类号:P228 9 文献标识码:A 文章编号:1674-098X(2021)01(a)-0015-03
Abstract: The influence of the projection parameters of the defined coordinate system on the transformation of plane Cartesian coordinates is analyzed by an example. It is found that the central Meridian is the most important projection parameter, and the difference of other projection parameters has little influence on the result. It is pointed out that only when the central Meridian of two sets of coordinate systems is the same, the conversion accuracy will be greatly reduced if there is difference, and it is necessary to carry out the conversion step by step to ensure the conversion accuracy.
Key Words: Rectangular coordinates; Coordinate transformation; Projection parameter; Central meridian
測量中,多种平面直角坐标系的并存,使得平面直角坐标转换技术在工作中使用频繁,研究投影参数的差异对坐标转换成果的影响,是成功实现平面直角坐标转换计算的关键,是获得可靠转换成果的保证。
1 概述
1.1 平面直角坐标系的种类
由于多种原因,我国有多种平面直角坐标系并存的情况。应用较多的有基于54参考椭球的平面直角坐标系、基于80参考椭球的平面直角坐标系、基于WGS-84地球椭球的平面直角坐标系、基于2000地球椭球的平面直角坐标系等。实际测量工作中,为了得到不同坐标系下的平面直角坐标,经常采取坐标转换方法,求解不同坐标系之间的变换关系,获取不同坐标系下的坐标成果,使工作达到事半功倍的效果。
1.2 投影参数的概念
在我国城市测量与工程测量中,普遍采用“高斯一克吕格投影”。由于该投影为横轴等角切圆柱投影,具有中央子午线上的点,投影长度不变,而偏离中央子午线越远的点,其长度变形也越大。为了减小长度变形,提高测量精度,一般各地方都建立适合于本地区的地方独立坐标系。为建立独立坐标系,要确定坐标系的中央子午线、起算点坐标、起算方位、起算边长、投影面高程、参考椭球、平移参数、旋转参数、尺度参数等,正是在这些投影参数的基础上,独立的平面直角坐标系才得以产生。定义某种坐标系时,使用到的各个指标统称投影参数。在进行平面直角坐标转换时,这些投影参数对转换结果会产生不同影响。
1.3 坐标转换的方法
实现平面直角坐标转换的方法较多,常用的有平面三参数转换模型、平面四参数转换模型、平面六参数转换模型、拓扑变换、多项式逼近法等。转换方法多种多样,但是无论那种转换方法都与坐标系建立时的投影参数密不可分,与高斯一克吕格投影的特点密不可分。实际工作中,转换模型的选取对转换结果的影响可忽略不计。本文不做研究。
2 实例验算
以平面四参数转换模型为例,进行实际演算,分析投影参数的差异对转换结果的影响。
2.1 平面四参数转换模型(赫尔默特法)的简要介绍
平面四参数转换模型是基于笛卡尔直角坐标系而建立起来的一种坐标变换数学模型,通过两个坐标系的平移、旋转和尺度变化来实现的,又称相似变换,至少需要两个公共点。平面四参数转换模型为:
2.2 转换精度评定和评估方法
在平面直角坐标转换后,应根据转换模型计算的重合点的残差中误差来评估坐标转换的精度。如在两个坐标系统下有n个重合点,坐标转换精度估算公式如下:
V(残差)=重合点的转换坐标-重合点已知坐标
对平面坐标有:x残差中误差;y残差中误差,则平面坐标点位中误差为。
2.3 实例验算
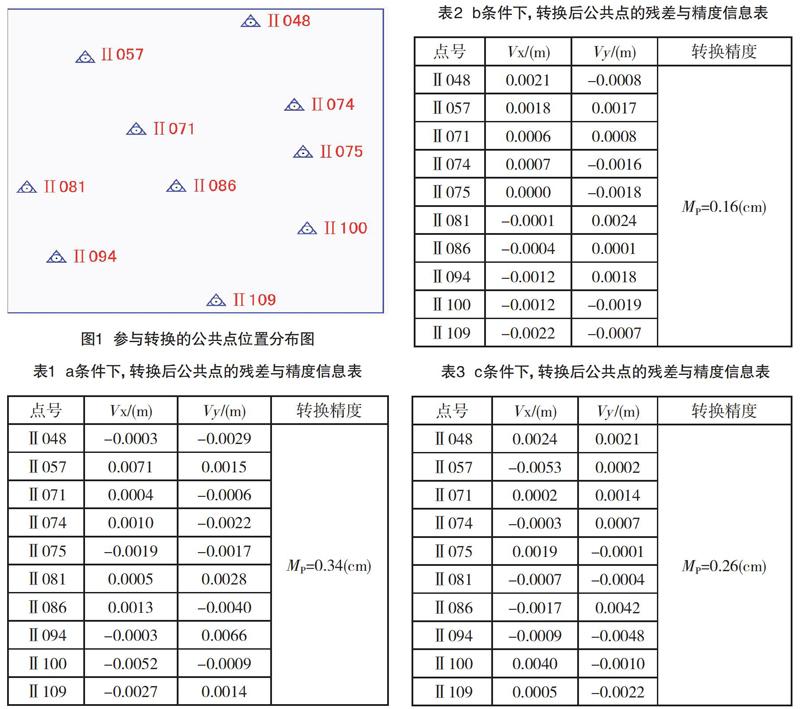
采用某城市基础平面控制网整合项目数据,该市因历史原因,不同部门间共定义有6套坐标系,数据丰富。在100km2的范围内选取10个公共点进行验算。点位分布如图1所示。
2.3.1 中子午线相同时
(1)两套坐标系存在平移、旋转和尺度差别时,残差与转换精度如表1所示。
(2)两套坐标系存在投影面高度差异时(投影面高相差500m),残差与转换精度如表2所示。
(3)两套坐标系既存在平移、旋转和尺度差别又存在投影面高度差异时,残差与转换精度如表3所示。
2.3.2 中央子午线不同时(分别为114°和114°45′)
两套坐标系其他投影参数相同或几无差异时,残差与转换精度如表4所示。
2.4 演算结果
上述演算可知,两套坐标系中央子午线相同时,残差为毫米级,转换精度理想;中央子午线不相同时,残差为分米级,精度低,不可靠。可见,中央子午线的差异对转换结果可产生数量级的影响。
3 理论分析
平面直角坐标转换的實质是两套坐标系通过数学模型进行强制匹配。椭球参数、平移参数、旋转参数及起算点坐标、起算方位、起算边长的差异所产生的两套坐标系在坐标转换的过程中可以通过平移、旋转和尺度消除;投影面高程的差异形成的两套坐标系在坐标转换的过程中也可以通过尺度消除;但中央子午线不同时,因受高斯投影特点的支配,形成的两套坐标系在坐标转换的过程中无法通过平移、旋转和尺度来消除,所以只有在两套坐标系的中央子午线相同时,才无需考虑由此而产生的影响。
4 结论
(1)在平面直角坐标转换时,众多的投影参数中,中央子午线的差异对转换结果会产生很大影响,而其他投影参数的差异对转换结果影响很小可忽略不计。
(2)在实际的平面直角坐标转换中,只要保证公共点的两套平面直角坐标的中央子午线相同,即可进行转换,可获得理想的转换成果。当两套坐标系的中央子午线不同时不能进行直接转换,需分步进行转换,使得中央子午线一致后,再行转换。
(3)建立新的2000国家大地坐标系时,在旧坐标成果的匹配和延用上,遵循此结论,才能发挥出坐标转换的强大优势。
参考文献
[1] 薛君,张帆.工程测量中GPS坐标转换算法分析与设计[J].轻工科技,2019,35(1):82-83.
[2] 曾富全,庞咏.坐标系转换及相关问题的探讨[J].云南地质,2017,36(2):302-306.
[3] 刘山洪,邓彩群.坐标转换与坐标变换研究[J].吉林建筑大学学报,2016,33(1):43-47.
[4] 张宇.河道独立坐标系建立方法的研究[D].西安:西安科技大学,2017.
[5] 王兵刚.测量坐标转换模型研究与系统程序实现[D].上海:东华理工大学,2015.
[6] 高开强,徐泮林,赵晓旭.RTK坐标转换参数的应用与精度分析[J].测绘与空间地理信息,2019,42(8):108-113.
[7] 谢剑,郭先锋,赵雅君,等.坐标系转换[J].勘察科学技术,2017(S1):169-172.
