基于深度学习的能源系统需求响应短期负荷预测

黄远明，黄志生，周睿，向德军

（广东电力交易中心，广东广州 510000）

可再生能源以其自身的安全可靠、利用率高以及环境友好等特点，有效促进了能源的消纳和利用[1-3]。能源系统电力预测可实现能源的有效规划，同时也是保障能源系统可靠运行的基础[4]。需求响应（Demand Response，DR）是指在有效确保能源系统平稳可靠运行的基础上，通过提升能源系统收益，使用户在电价调整信号的作用下，改变原有用电习惯的短期行为。通过需求响应技术，可以在一定程度上提高负荷侧相关数据的挖掘效率，在一定程度上延缓电力需求的紧张状况[5]。

由于能源系统短期负荷预测过程中存在复杂度高、不确定性强的特点，因此，准确的能源系统负荷分析和高精准预测模型的建立是能源系统负荷预测的关键之处[6]。传统的短期负荷预测方法虽然可以测得负荷变化，但是难以精准地描述负荷变化情况，而深度学习为一种全新的机器学习算法[7]，具备优秀的数据处理能力。为此，文中提出一种栈式自编码神经网络（SAE-NN），在充分考虑能源系统需求响应的基础上，实现能源系统短期负荷预测。

1 能源系统需求响应短期负荷预测

1.1 SAE-NN深度学习模型的构建

由于在短期电力负荷预测过程中需要分析的环境数据和其他外部因素比较复杂，尤其是天气因素、日期和时间类型等，容易影响预测结果的准确性[8]。而深度学习算法是一种能够模拟出人脑神经结构的机器学习方法，突破了传统神经网络对分层节点数目的限制[9]。因此，可以较好地解决复杂因素影响下，短期电力负荷预测准确性的问题，为此构建栈式自编码神经网络（SAE-NN）深度学习模型。

栈式自编码器（SAE）和逻辑回归（LR）模型共同组成了栈式自编码神经网络（SAE-NN）深度学习模型[10]。SAE 模型处于SAE-NN 底层，由若干稀疏自编码器罗列而成，为去除解码层[11]。将当前自编码隐藏层l的输出h(l)视为下一自编码隐藏层l+1 的输入x(l+1)，表达式为：

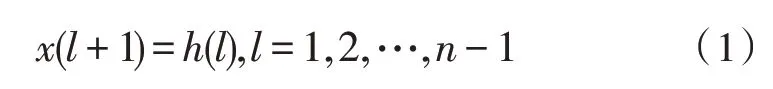
式（1）中，n表示底层SAE 模型中自编码器的数量。

能源系统的负荷不仅受到自身特性、气象类型、温度以及日型等因素影响，还受到用户需求响应负荷调整变化的影响[12]，所以在SAE-NN 模型中输入相关负荷资料、气象类型、温度、日型外，还需增加参与需求响应的负荷调整数据，以便提升能源系统短期负荷预测精度。

为了在能源系统中实现短期负荷预测目标，需要将LR 模型与底层SAE 模型相结合进行负荷预测，组成SAE-LR 模型，选择sigmoi 非线性神经元作为该模型的输出节点[13]。利用SAE 对输入样本x(l)展开多次变换后，获取包含重要预测目标信息的输入样本的n阶特征h(n)，并将其作为LR 模型的输入进行能源系统短期负荷预测。利用SAE 模型得到的不同层阶的特征作为预测器的初始输入，有效提升了网络泛化能力，并采用无监督方法训练SAE-NN模型，获取最优SAE-NN 预测模型。

1.2 负荷预测的实现

多数现有电力负荷预测方法纳入计算的因素较为单一，导致负荷预测结果不准确，不利于制定发电计划及电力发展规划。文中研究的电力负荷预测方法考虑了能源系统的需求响应负荷，并对其数据进行调整，以此提高预测结果的精度。

调整需求响应负荷的内容有：中断负荷和可转移负荷。在能源系统需求响应发布之后，系统中的用户就会根据发布的需求调整当前的用电负荷，并根据真实情况进行负荷转移或者中断操作[14-15]。在整个能源系统需求响应过程中，用户主要基于电价和舒适度两个角度调整负荷响应系统需求。分时电价需求响应和应急需求响应是能源系统需求响应的两种主要方式，其中应急需求响应执行后，主动降低负荷的用户会得到一定的奖励[16]。电价和舒适度分别从用户经济效益和用户舒适度体验两个角度影响着用户的需求响应程度[17]。

1）可中断负荷收益模型

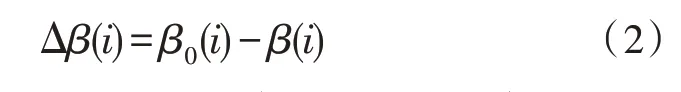
式（2）中，β0(i)和β(i)分别表示初始需求量和经济奖励后的需求量。采取应急需求响应后的总经济奖励为：

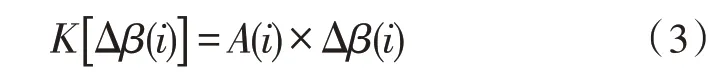
式（3）中A(i)表示时间段i的经济奖励，则时间段i时用户收益S的表达式为：

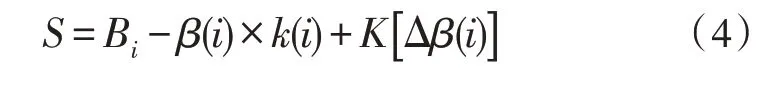
式（4）中，Bi用于描述经济奖励补偿前，处于时间段i内的用户供给量；k(i)表示补偿后的电价。

求解式（4）的偏导数[18]，使得，那么此时用户收益达到最大值：

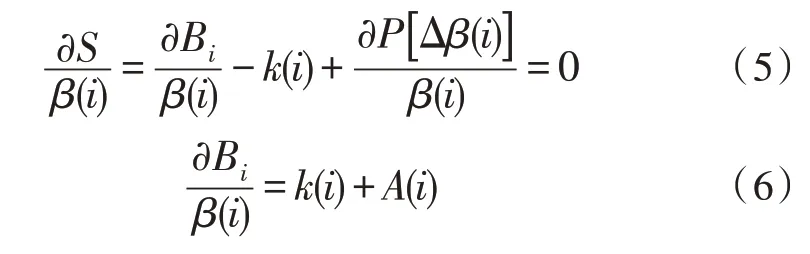
则用户收益函数计算表达式：

式（7）中，B0(i)、K0(i)分别表示初始收益、初始电价，E(i)表示价格弹性。

综合式（5）、（6）可获取用户用电需求：

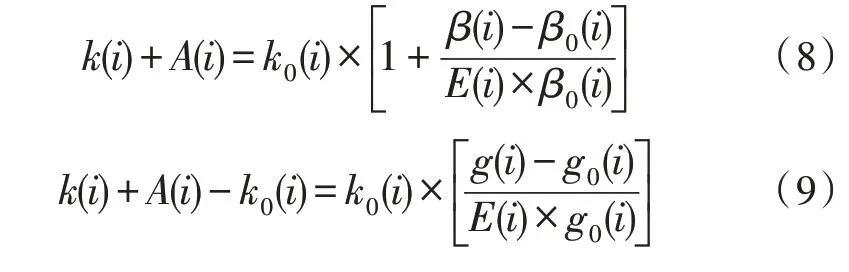
那么，用户需求响应函数表达式为：

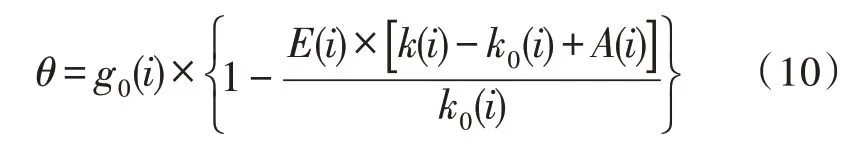
式（10）中，若k(i)的值为0，表示该时间段无经济奖励，此时的电价未产生变化，不存在价格弹性[19]。

2）可转移负荷收益模型

设定时间段i、j重叠部分的价格弹性表达式为：

若时间段i和时间段j为同一时间段，即i=j，那么E0(i,j)≤0；若时间段i、时间段j为不处于同一时间段，即i≠j，那么E0(i,j)≥0。

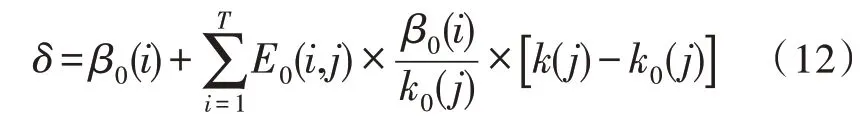
假设应急需求响应方式下，时间段j的经济奖励用ω(j)描述，那么将其引入电价中可获取：

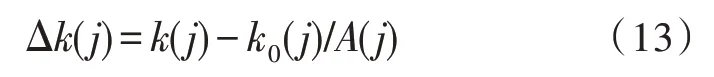
当能源系统负荷处于用电高峰阶段时，A(j)为正数，当能源系统负荷处于非高峰阶段时，A(j)为0。

综上，计及电价和经济奖励的可转移负荷模型中用户需求响应函数表达式为：

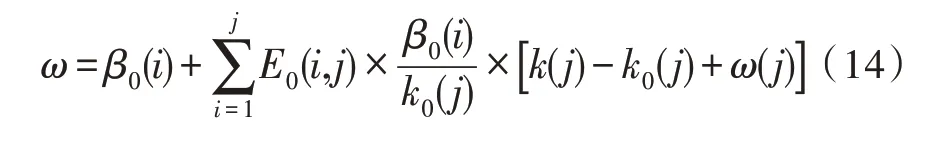
遵循可中断负荷模型以及可转移负荷模型的需求响应函数，式（15）为能够中断的负荷、能够转移的负荷合并预测的模型，表达式为：

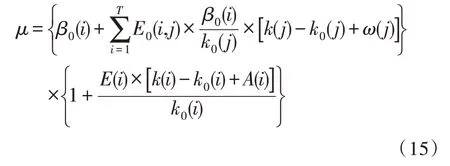
3）舒适度判断

基于电价角度分析用户收益，实现负荷调整是负荷调整的一个方面，舒适度角度是负荷调整的另一个方面。温度变化和功率变化是用户舒适度的两个重要指标[20-21]。设定由温度变化引起的舒适度用φw表示为：

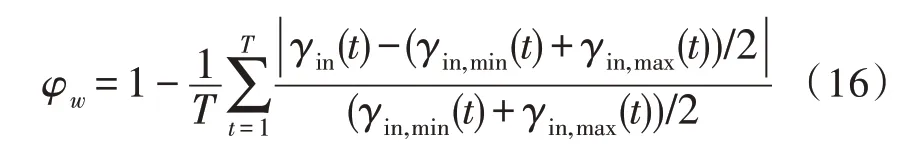
式（16）中，γin(t)、γin,min(t)、γin,max(t)分别表示实际温度、最小温度、最大温度；(γin,min(t)+γin,max(t))/2 表示预计温度、T为预计时间周期。

伴随功率的变化用户的舒适度也会发生变化，用φp来表示发生变化的舒适度，其表达式为：

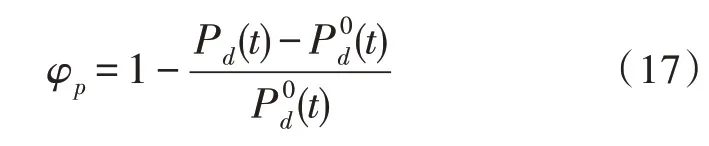
采用几何加权方式结合温度和功率的舒适度评判公式[22]，获取用户舒适度评判方程μcomfort为：

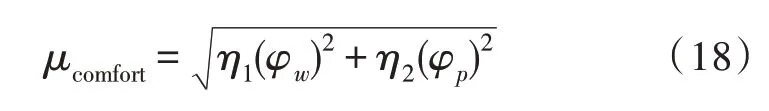
式（18）中，η1表示温度变化对用户舒适体验影响的权重系数，η2表示功率变化对用户舒适体验影响的权重系数[23]。

综上可知，基于需求响应某时间段的用户负荷调整的判断条件为：

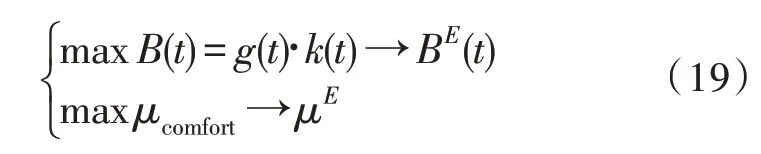
式（19）中，B(t)、maxB(t)分别表示用户预期收益、预期收益最大值；μcomfort、maxμcomfort分别表示用户舒适度、舒适度最大值；BE(t)表示某时间段的预期收益，μE表示某时间段的预期用户体验舒适度。如果用户收益和舒适度都满足了预期，那么负荷就会得到调整。如果用户收益和舒适度都不满足预期，就不需要调整。

若使用者的真实收益与预计收益接近，则将一部分能够调整的负荷转移到其他时段。若使用者的真实体验舒适度略高，就利用部分调整负荷的方式，中断可调节的负荷。如果使用者的收益和舒适度均未满足预期，则无需进行负荷调整；如果真实舒适度略高，但预期收益略低时，就利用部分调整负荷的方法，中断可调节的负荷。

因此，预期收益和舒适度为需求响应过程中影响负荷变化的重要因素。能源系统短期负荷预测中，应重点考虑这两个因素，以提升短期负荷的预测精度。

为了有效地获取能源系统负荷的内在变化特征、外在变化特征与负荷变化之间的内在联系，利用SAE-NN 模型进行负荷预测[24]，预测流程为：

1）修改、补充得到能源系统的非正常数据和丢失数据，并采用式（20）按照[0,1]标准进行归一化处理后，对样本数据实施重构以便获取符合SAE-NN预测模型的输入、输出要求。

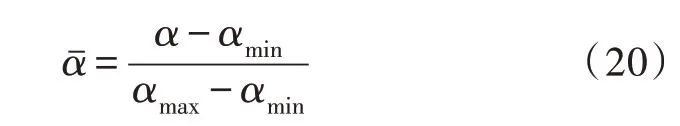
式（20）中，αˉ为归一化后的数值，α为归一化前的样本数据；αmax为归一化前数据中的最大值，αmin为归一化前数据中的最小值。

2）将训练样本输入SAE-NN 模型中进行训练，获取重构后的负荷、气象、温度、日型、需求响应等数据，微调参数后获取最优预测模型。

3）在最优SAE-NN 中输入测试样本，预测能源系统短期负荷，并利用预测结果对模型性能实施评价。

2 仿真实验与分析

选取某市某纺织工业园区2019 年6 月1 日至2019 年7 月31 日的实际运行数据为样本验证所提方法的预测性能，信息采样频率为10 min。将6 月1 日至7 月21 的数据作为训练样本，剩余数据作为测试样本，采样点缺失样本不参与计算。实验在Matlab 2015a 平台进行，运行系统为Windows2010，Intel core i5 9400 CPU，8 GB 运行内存。

基于上述数据与实验环境，为验证所提方法对短期负荷预测的精度，对比充分考虑用户预期收益和用户舒适度需求响应的短期负荷预测结果，和未考虑该方面的预测结果，经过100 min 的测试，并以实际负荷作为参考，越接近实际负荷值说明预测精度越精准。实验对比结果如图1 所示。

图1 未考虑需求响应、考虑需求响应的预测值与实际负荷对比

由图1 数据可知，相较于未考虑需求响应的模型预测值，考虑基于用户预期收益和用户舒适度需求响应后的模型预测结果与实际负荷结果更加接近，说明在模型中计及需求响应可显著提升模型的预测精准度。原因在于文中方法在预测模型中不但加入了能源系统负荷的内在变化特性及气象特征、温度、日型等外在影响因素，还充分考虑了需求响应下的负荷调整，因此，文中方法的预测精度较高，可得到与实际负荷值基本一致的负荷预测值。

为进一步验证所提方法的预测性能，选择基于支持向量机（SVR）模型的短期负荷预测方法以及基于GRU-NN 模型的短期负荷预测方法为对比方法，选择相对误差（RE）、平均绝对误差（MAPE）、均方根误差（RMSE）以及希尔不等系数（TIC）4 个指标为预测结果评估指标，对研究区域的短期负荷进行预测。各个指标评估结果如表1 所示。

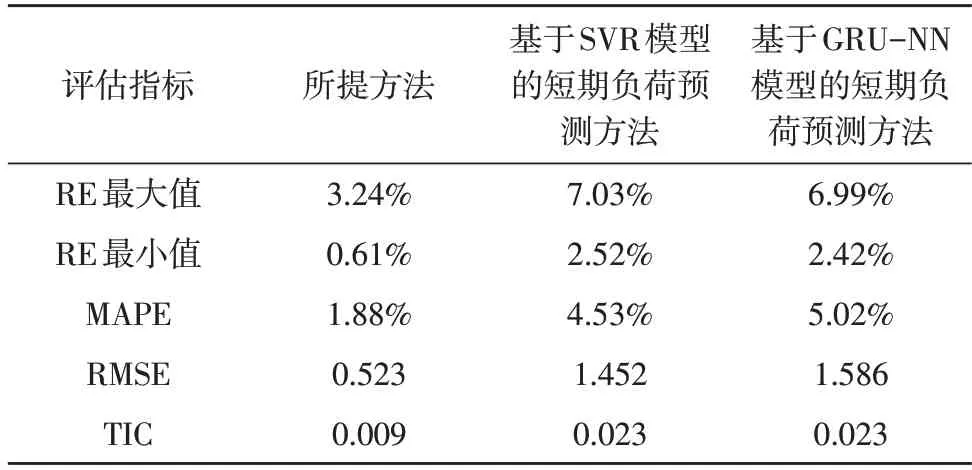
表1 各指标评估结果

分析表1 数据可知，文中方法的负荷预测相对误差（RE）最大值为3.24%，相比另外两种对比方法的负荷预测最大相对误差分别小3.79%、3.75%；所提方法的负荷预测相对误差（RE）最小值仅为0.61%，远远小于对比方法的负荷预测相对误差最小值。表明文中方法的短期负荷预测误差波动范围较小，负荷预测结果精确度高。平均绝对误差（MAPE）可有效衡量预测结果的整体预测精度，从表1 可知，文中方法的预测MAPE 仅为1.88%，显著低于另外两种对比方法，结果表明所提方法的短期负荷预测误差低，短期负荷预测效果较好。文中方法负荷预测均方根误差（RMSE）为0.523，显著低于另外两种对比方法，结果表明所提方法的非线性拟合能力强，获取的短期负荷预测结果与实际负荷值间的偏差较小，预测精度较高。希尔不等系数（TIC）可有效体现估计值与真实测量值的差别，TIC 的值越小两者之间的差异越小。如表1 所示，另外两种对比方法的TIC值均为0.023，所提方法的TIC 值仅为0.009，所提方法的差异数值小于对比的两种方法。

综上可知，文中方法具备较高的短期负荷预测精度。原因在于所提方法利用SAE 逐层学习提取深层特征，利用LR 模型预测能源系统短期负荷，进而提升了短期负荷预测的精度。

3 结论

文中研究有效利用基于深度学习算法的优秀信息表达能力，采用由底层栈式自编码器（SAE）和顶层逻辑回归（LR）模型组成的栈式自编码神经网络（SAE-NN）模型预测能源系统短期负荷。为提升预测精度充分考虑需求响应对能源系统的负荷调整，将需求响应与气象类型、温度以及日型等因素共同作为预测模型输入。仿真分析验证了文中方法具备较高预测精度和预测可行性。