基于二阶广义积分的单相有源电力滤波器

李 斌，肖景瑞，吴贵民

（1.国家电网公司直流建设分公司，北京 100000；2.国网黑龙江省送变电工程有限公司，黑龙江哈尔滨 150000）

在构成有源电力滤波器（Active Power Filter，APF）的各种组件中，数字信号处理器和电压传感器是成本最高的两个组件[1]。众所周知，使用电压传感器有助于提高APF 性能，但也会极大增加系统的复杂性和成本[2-4]，且尺寸较大。

目前，对无电压传感器单相APF 的研究比较少。为了降低系统成本，文献[5]仅使用一个电流传感器（负载侧）设计了并联混合型APF。文献[6]设计了一种无电压传感器的三相APF，并在三相线上使用了两个电流传感器，可以根据实际测得的相位进行估计计算。然而，大多数非线性负载是为低功率应用而设计的，这些负载可能具有高功率因数和高电流谐波。基于此，文中借鉴上述研究成果，提出了一种无电压传感器单相APF，可以有效抑制低功耗单相负载的谐波电流，并降低系统成本。在该系统中，仅使用两个电流传感器来测量负载电流和转换器电流。因此，不需要PI 调节器，也不需要进行其他计算便可确定功率损耗。

1 无电压传感控制器

文中所研究APF 的电源电路是一个具有直流电容Cdc的单相H 桥PWM 转换器。通过调节直流链电容上的电压并控制参考滤波器电流，以补偿栅极电流的电流谐波。电压源转换器（Voltage Source Converter，VSC）[7]的交流侧通过电感Lc连接到公共耦合点（Point of Common Coupling，PCC），流经电感的电流由电流互感2(CT2) 测量。在直流侧，电阻(RL)和电感(LL)元件组成的全桥二极管整流器提供非线性负载[8]。

使用电流互感1(CT1)测量非线性负载所消耗的负载电流，基于负载和滤波器电流测量，传统单相APF 的原理框图如图1 所示。

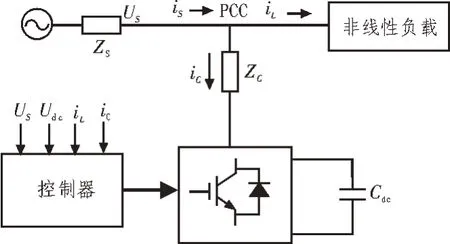
图1 传统的单相APF的原理框图

众所周知，单相非线性负载会产生正弦电流，可以将其表示为：

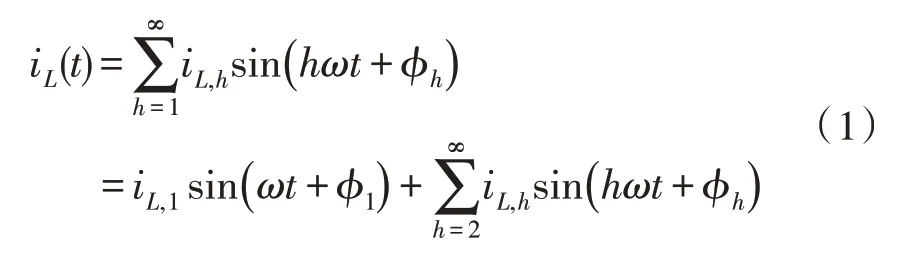
式中，h是谐波阶次，φh是谐波相位角，ω是基波谐波的角频率。从式（1）中可以看出，负载电流iL由基波电流iL,1和谐波电流{iL,h}h≠1 组成，即：

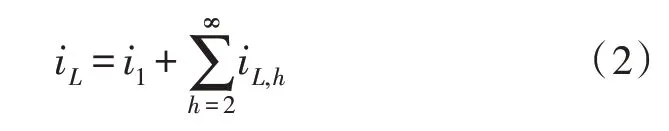
其中，通过CT2测量负载电流iL。APF 的主要目的是动态抑制所有谐波电流ih，为此，控制电路需要确定参考补偿电流，则VSC 需要生成补偿电流ic，该电流等于反相谐波，即：

该补偿电流由APF 注入PCC，并获得以下正弦栅极电流：

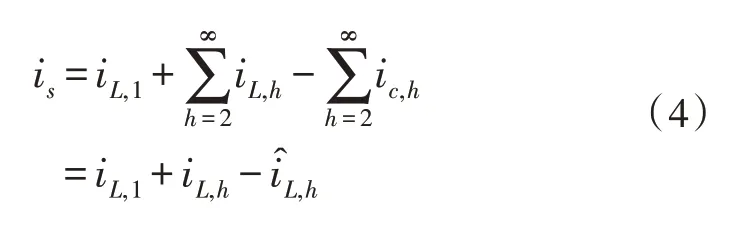
因此，得到的栅极电流波形将是正弦曲线，其形状为：

从式（6）中可以看出，确定参考栅极电流对于单相APF 控制电路非常重要。可以通过将栅极电流的幅值Is乘以正弦函数来计算参考栅极电流，即：

栅极电流的幅值Is主要根据PI调节器确定，即：

式中，kp和ki是直流链PI 调节器的比例和积分增益。为此，从实际测量的直流链电容电压udc中减去预先设定的直流链电容电压可得出瞬时误差Δudc：

在本研究中，低功率APF 的参考栅极电流i*s由负载和补偿电流来确定，如图2 所示。

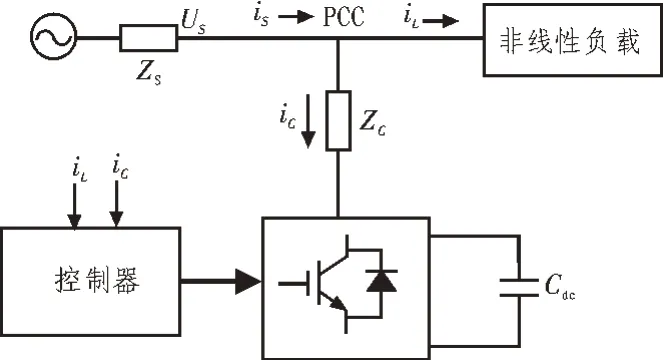
图2 单相APF的原理框图

在文中所提出的方法中，首先通过CT1对测得的负载电流iL(t)进行检测，然后采用二阶广义积分[9]（Second-Order Generalized Integrator，SOGI）算法对其进行处理。SOGI 的特征传递函数为：

且

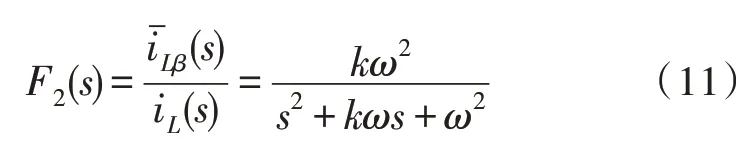
其中，ω是输入信号的角频率，且k是SOGI 的阻尼因数[10]，将频率ω调谐至314 rad/s，输入信号的频率等于调谐频率ω，F1(s)充当带通滤波器（BPF），F2(s) 充当低通滤波器（LPF）。输入信号iL(t) 和式（10）中的信号具有与基波谐波相同的相位和幅值。因此，可以将视为参考栅极电流，即：

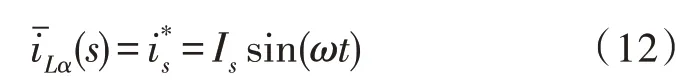
补偿电流误差Δic用于驱动VSC 开关（S1、S2、S3和S4），PCC 上的实际补偿电流ic由磁滞电流控制器控制。该控制器的结构简单，已广泛用于有源滤波器应用[11-14]。提出的无电压传感器单相APF系统如图3所示。

图3 基于SOGI的无电压传感器单相APF

2 实验结果与分析

2.1 仿真结果

首先使用Matlab/Simulink 对文中所提无电压传感器单相APF 进行仿真，以进行性能验证。两种不同的非线性负载（负载1 和负载2）被用于观察基于SOGI 的单相无电压传感器APF 的动态性能。仿真系统使用的参数如表1 所示。

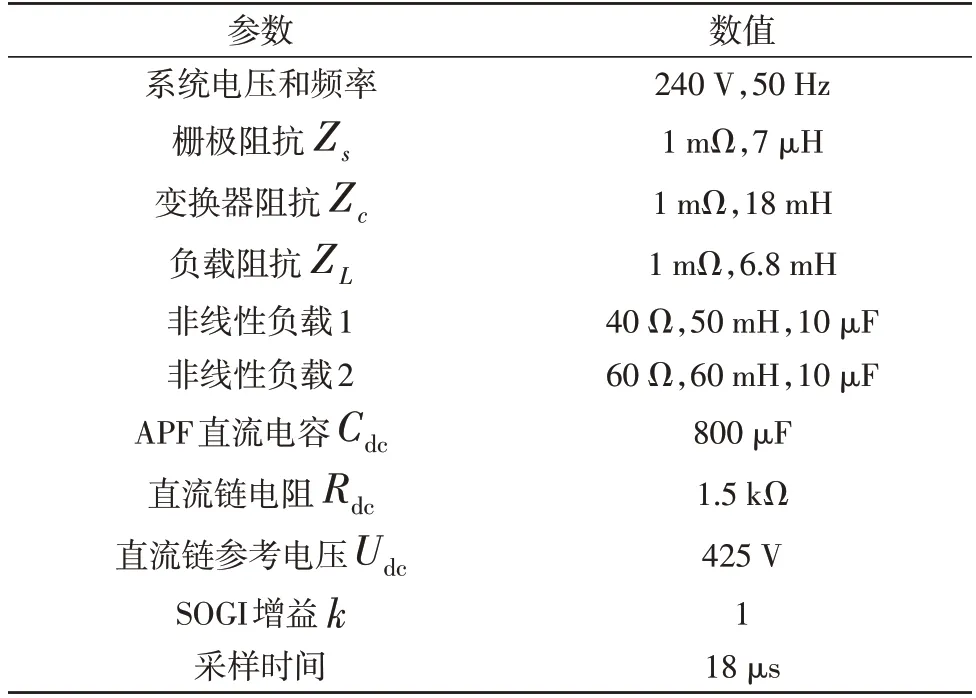
表1 仿真系统参数

负载电流波形如图4 所示，向PCC 注入的补偿电流如图5 所示，获得的栅极电流波形如图6 所示，最终直流链电压波形如图7 所示。

图6 栅极电流波形

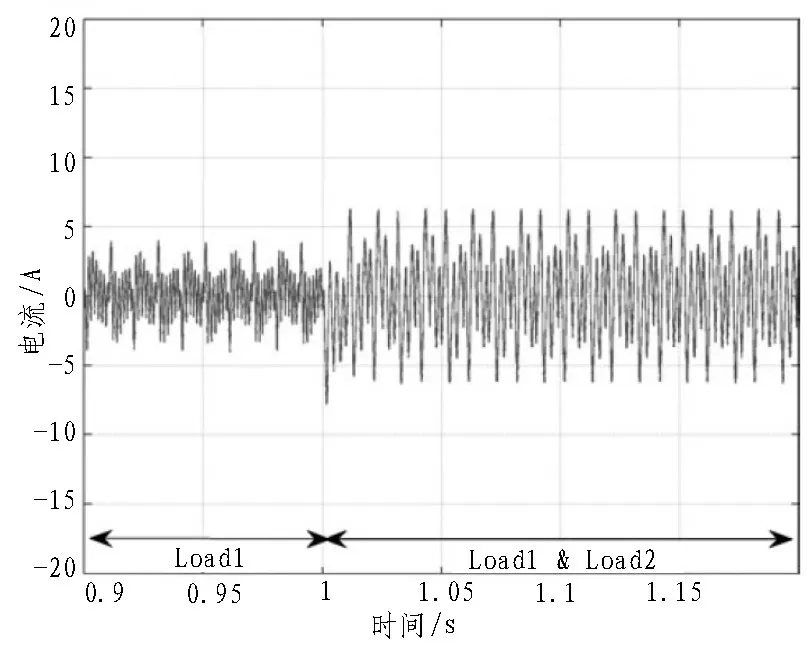
图5 补偿电流波形

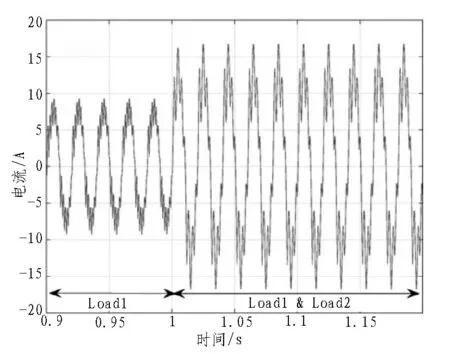
图4 失真的负载电流波形

从图7 可以看出，电容充电时直流链电容电压Udc稳定上升，然后电压Udc呈平稳状态，这在很大程度上取决于直流链电阻Rdc的稳定作用。需要注意的是，若未提供电阻Rdc，则电容电压将继续上升，这会对开关电路产生不利影响。

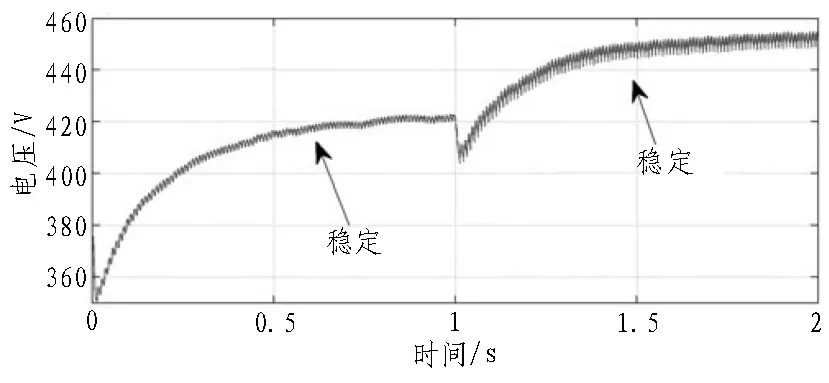
图7 直流链电压波形

2.2 真实测试结果

使用OP5600/RT-LAB 实时仿真平台[15-16]和FPGA 硬件进行了验证，以观察所提无电压传感器单相APF 在真实环境中的性能。具体来说，使用Xilinx系统生成工具在FPGA 上实现了提出的单相无电压传感器APF，测试中充分考虑了实时测量实际信号和实现控制信号所需的延迟。真实测试中使用的参数同表1 中数据一致。通过数字示波器观察实验结果，如图8 和图9 所示。

图8 （CH1）栅极电流、（CH2）补偿电流、（CH3）负载电流和（CH4）源电压

图9 滤波后的（CH1）栅极电流、（CH2）补偿电流、（CH3）负载电流

负载电流（Load1）的总谐波失真为27.35%，而均方根电流为5.51 A；当负载1 和负载2 都与栅极相连接时，均方根电流增加到9.17 A，且总谐波失真为24.85%。栅极电压uc和负载电流iL的波形如图8 所示（CH4 和CH3），其中，在CH3 中可以看到负载电流iL严重失真。

控制器所注入的转换器电流ic如图8（CH2）所示，栅极电流波形如图8（CH1）所示。最终的栅极电流、补偿电流和负载电流如图9 所示。因此，在第一个负载组合中，栅极电流的总谐波失真降低到4.03%，在第二个负载组合中降低到3.76%，符合推荐的IEEE 519-1992 标准。

3 结论

文中提出了一种基于SOGI 的单相APF。该单相APF 无需电压传感器，仅使用两个电流传感器来测量负载和转换器电流，成本较低。同时，不需要使用PI 调节器，也不需要计算负载电流幅值。因此，相关的控制电路不需要特殊的算法来处理栅极电压，大大降低了系统的复杂性。仿真和实时实验结果研究验证了文中控制技术的有效性。但是，在电压波动和频率变化的情况下，所提系统的动态补偿性能仍需要进一步验证，这也是后续研究的重点。