基于图覆盖的改进复杂网络免疫策略
2021-06-11肖詠
肖詠
摘 要: 提出一种基于图覆盖的改进复杂网络免疫策略。该方法引入模拟退火的思想,利用局部信息,以节点度大为原则选取免疫节点,同时以一定的概率接受度小的节点。使用交互式邮件传播模型,在真实的网络数据集上从免疫效率和免疫代价的角度进行了对比实验。实验结果发现,改进的方法在一些社团结构明显的网络中具有更好的效果,从而验证该方法的有效性。
关键词: 图覆盖; 免疫策略; 模拟退火; 免疫效率; 免疫代价
中图分类号:TP391 文献标识码:A 文章编号:1006-8228(2021)05-53-05
An improved complex network immunization strategy based on graph covering
Xiao Yong
(Information Technology Center, Chongqing Medical University, Yuzhong, Chongqing 400016, China)
Abstract: An improved complex network immune strategy based on graph coverage is proposed. This method introduces the idea of simulated annealing, uses local information, selects immune nodes according to the principle of large node degree, and accepts nodes with small degree with a certain probability. Using the interactive e-mail propagation model, a comparative experiment is conducted on real network data sets from the perspective of immune efficiency and immune cost. The experimental results show that the improved method has better effect in some networks with obvious community structure, which verifies the effectiveness of the method.
Key words: graph covering; immune strategy; simulated annealing; immune efficiency; immune cost
0 引言
現今,复杂网络的病毒传播相关研究已经成为复杂网络的重要研究分支,近年来的研究表明,网络的拓扑结构小世界和无标度特性,在很大程度上影响病毒的传播行为,在现实复杂网络中,发生少量病毒感染源即使病毒传播速率非常低,也可以在网络中广泛蔓延开来[1-3],故挖掘有效的免疫策略来控制病毒的爆发与传播具有重大现实意义。针对免疫策略,人们做了大量研究,提出了以随机免疫[4],目标免疫[5],熟人免疫[6],图覆盖免疫[7]为代表的一系列免疫策略。本文在图覆盖免疫的基础上,结合模拟退火思想,提出了一种改进的策略。通过在真实社团网络数据集上的实验,验证了本文策略具有更好的免疫效果。
1 复杂网络免疫策略
复杂网络一般用图来表示,一个具体的网络可抽象为图G=(V,E),由节点集V(vertex)和边集E(edge)组成,免疫的核心思想就是想办法找到一些重要的点,提前采取保护措施来降低节点感染的概率,从而阻止病毒的传播。
随机免疫,不考虑节点和网络拓扑结构的差异,在网络中随机选取一定比例的节点进行免疫,发现在均匀网络中是有效的,而在大规模无标度网络中几乎需要免疫所有节点才能控制病毒的传播,显然,这是没有意义的。
目标免疫,其核心思想是找到网络中一部分重要节点进行免疫,以节点度为代表,这是利用了无标度网络中大部分节点的度很小、小部分节点的度很大的特性,一旦控制住了度大的节点,其他节点被感染的几率会显著降低,花费比较小的代价起到了很好的控制效果。然而作为一个全局性的免疫策略,目标免疫必须遍历掌握整个网络的拓扑结构,对于现实大规模和动态网络,实施难度显而易见。
熟人免疫,试图找到一个方法既能克服目标免疫需要全局信息的缺点,又能达到目标免疫的效果,首先在网络中随机选取一部分节点,然后以他们为基础,再次随机选取他们周围一个或者多个节点进行免疫,因为无标度网络大部分节点的度很小,第一次随机到他们的可能性较大,他们往往连接着度大的节点,第二次随机到度大的节点概率也较大,故只需要局部信息,就可以获得比随机免疫好的效果,但是事实上,这种随机选择的方式,在效果上与目标免疫还是有一定的差距。
图覆盖免疫在熟人免疫的基础上加以改进,转换为一个图论覆盖问题,第一次仍然在网络中随机选取一部分节点,以他们为中心,再次选取d步以内邻居中度最大的节点进行免疫,d=1为选取节点的邻居节点,d=2为选取邻居的邻居节点,此方式也是利用了局部信息,第二次有目标的选择使得它具有比熟人免疫更好的免疫效果。
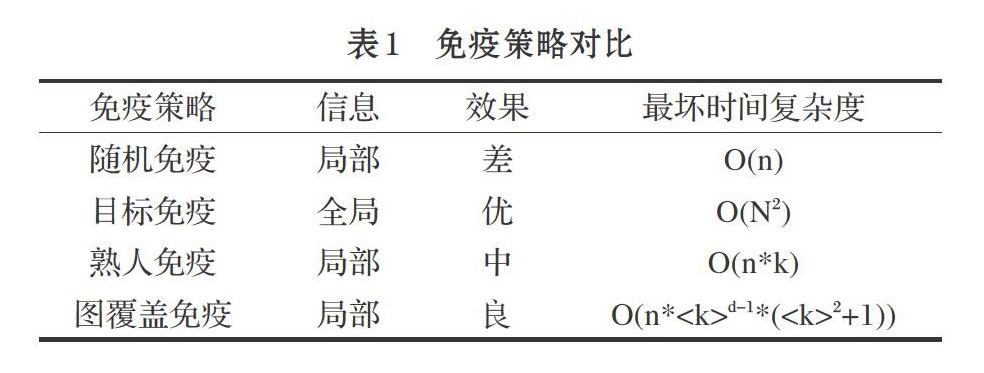
表1为不同免疫策略对比[8],其中N为节点总数,n为免疫节点数,
2 改进的免疫策略
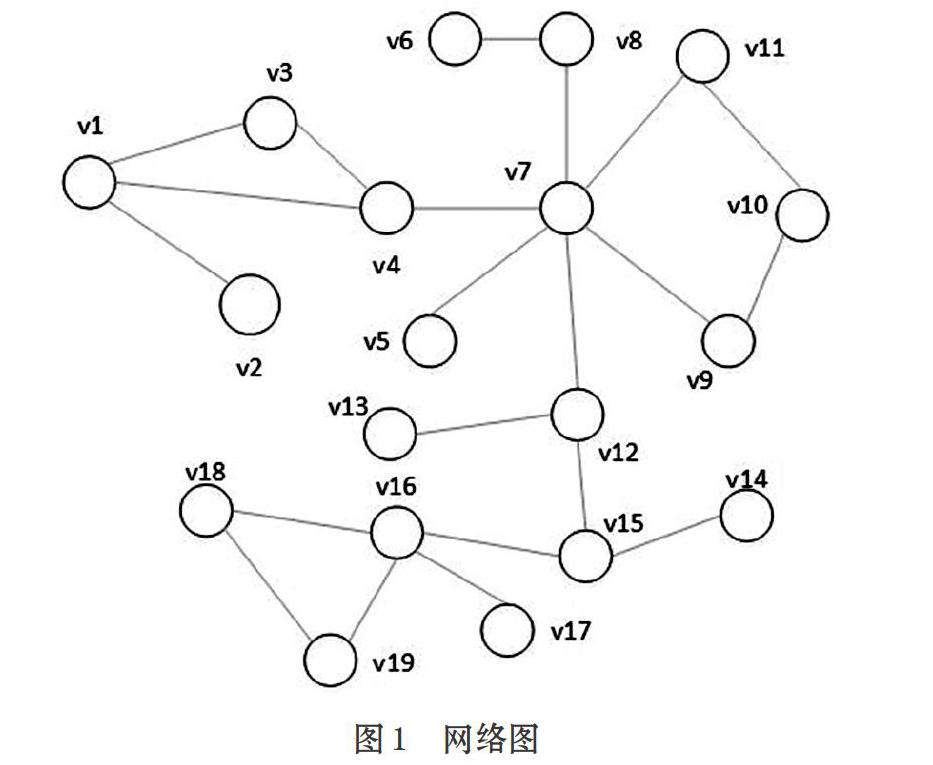
图覆盖免疫策略能够以局部信息获得较好的免疫效果,在现实网络中具有较好的操作性,但该策略选择节点行为固定,受网络拓扑, 特别是社团结构的影响较大,常陷入局部最优解[8],以图1为例,该网络有明显的社团结构,假设第一次随机选择到种子节点v15,d=1时,根据图覆盖免疫的原理,第二次应选择v16,而我们发现v12尽管不是d=1时的最大度节点,但是它起到更为重要的作为,保护v12能够阻止病毒朝着v5-v11这个社团传播,从这个角度看,v16只是局部最优解,从全局看并不能起到最优的效果。
所以图覆盖免疫要避免在社团结构明显的网络中陷入局部最优解,就不能在第二次选择过程中只考虑度最大的节点,度小的节点也需要加以考虑,但是也不能直接选择度小的节点。这里,我们引入模拟退火的思想[9-10],通过模拟物理中高温物体的退火过程寻找全局最优解,首先产生一个初始解为当前解,随着温度的下降,以一定的概率接受非局部最優解为新解,使之跳出局部最优的陷阱,并重复这个过程至条件结束,开始温度较高时,接受较差解的概率也比较高,会有更大的机会跳出局部最优解,随着退火的进行即温度的逐步下降,算法接收较差解的概率也变小。故我们在第二次选取种子节点的邻居节点时,不是直接选取度最大的节点,而是以一定的规则去选取,定义选取的规则如下:
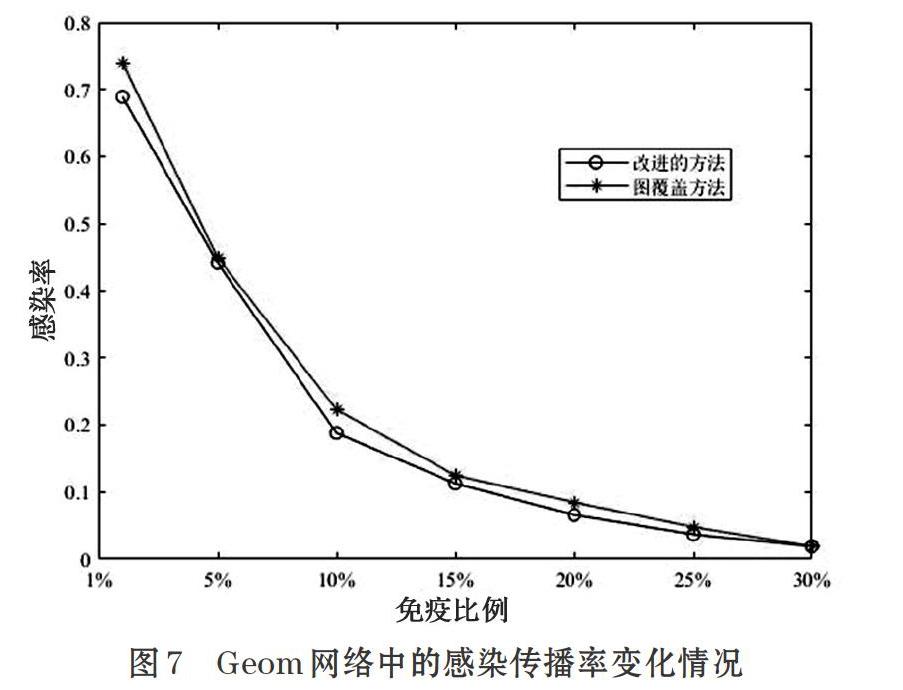
[Pvi=1, vj.deg 其中,T为温度,vj.deg为在遍历过程节点过程中临时解的度,vi.deg为目标节点的度。选取的过程如下。 ⑴ 在网络中第一次随机选取一部分节点,以它们为中心,假设取d=1,遍历它们的邻居节点。 ⑵ 初始化温度T,当前选取节点vj为初始解。 ⑶ 如果遍历到vi,节点vi的度大于vj的度,那么节点vi为新解,否则根据公示计算概率1/(1+exp((vj.deg-vi.deg)/T)),根据结果决定是否选取节点vi。 ⑷ 如果达到终止条件,则算法结束,否则按衰减函数得到新的温度T重复步骤⑵-⑷。 可以看出,开始温度较高时,选取度小的概率相对来说还比较高,随着算法迭代,温度不断降低,概率越来越低,并且目标节点的度越小,选取的概率越小,但是不代表一定不选取。为了更好的理解这个过程,我们还是以图1为例:假设第一次随机选择到种子节点v15,d=1,遍历v15的邻居节点,v16为初始解,开始设定温度为100,根据选取规则,选取v14的概率为49.25%,随着环境变化,假设温度下降到了10,选取v14的概率为42.56%,尽管概率变小,但还是有跳出局部最优解的可能。 改进后的免疫策略思路为:第一次在网络中随机选取一部分节点,以他们为中心,再次在d步以内的邻居中选取目标节点进行免疫,目标节点以尽量选取度大的为原则,同时以一定的概率接受度小的节点,以跳出局部最优解。 3 实验分析 3.1 实验数据集 本文选取NetScience网络数据集、Geom网络数据集来进行实验,NetScience[11]网络是一些科学家关于网络原理和实验研究的合作关系,Geom网络是科学家关于计算机几何学研究的合作关系,NetScience网络和Geom网络具有明显的社团结构,表2为它们的基本统计特性。 3.2 实验方案 尽管免疫的核心问题已经转化为找出一些重要的节点来进行保护,但评价一种免疫策略的有效性必须结合病毒传播模型,观察在病毒的传播过程中,是否有效地被抑制,本文选择交互式邮件传播模型[12]来观察实验结果。 在交互式邮件传播模型中,用户分为健康、危险、感染三种状态,病毒的传播主要与用户检查邮件的时间T和点击病毒邮件的概率C有关,T和C服从高斯分布,本文中T和C的设定与原文模型保持一致,即取T~N(40,202),C~N(0.5,0.32),算法步骤如下。 ⑴ 初始化网络结构。 ⑵ 初始化节点状态,选取感染节点。 ⑶ 根据免疫策略选取免疫节点。 ⑷ 针对每个节点,用户查看邮箱操作,如果检查邮件的时间满足,并且打开了病毒附件,则被感染,并且向邻居列表的所有用户发送病毒邮件,如果没有打开则默认恢复到健康状态。 ⑸ 更新下次查看邮箱时间。 ⑹ 输出每个时间步的感染节点数。 3.3 实验结果分析 当病毒在网络中的传播趋于相对稳定的状态时,通过对比被感染的节点数量来衡量免疫策略的效果,为了消除随机性对实验结果的影响,我们将对每次实验运行100次,取100次实验的平均值作为实验结果,算法时间步数为600,图覆盖半径d=1,初始随机感染节点数量为2,图2、图3为在2个网络数据集中取1%(分别为16、73个)的免疫节点后网络中被感染的节点数量随时间的变化趋势,实验结果表明,病毒攻击网络后,网络中被感染的节点快速上升,随着时间的增加,慢慢趋于平衡,对比原方法和本文改进的方法,采用本文改进的方法最终被感染的节点低于原方法,效果有所提升,在2个网络中分别提升约13%和7%。同时我们发现由于实验结果无法避免随机性,本文的方法也存在无法优于原方法的情形,出现这种情形是由于不是每次实验都会陷入局部最优解。 图4、图5为在不同免疫比例下被感染的节点数量,在同一免疫比例下,本文改进的方法效果优于原方法,随着免疫比例的提升,网络中被感染的节点数量明显下降,病毒的传播被控制在比较低的水平。 考慮免疫效率的同时,免疫代价也不可忽视,它也是衡量免疫策略有效性的一个重要指标,即采用较少的免疫节点使病毒感染传播率达到一个较低的水平,病毒感染传播率ρ=ρf/ρ0,ρf为采用免疫策略后的感染密度,ρ0为没有采用免疫策略的感染密度,感染密度为感染节点数与总节点数的比值,定义?c作为免疫临界值,表示当病毒的感染传播率ρ趋于0时,所需要的免疫节点比例值。本文对此设计了另一组实验,图6、图7的实验结果为网络中病毒感染传播率随免疫比例的变化情况,结果表明为了使病毒的感染传播率控制在一定比例下,在趋近免疫临界值时,本文改进的方法能够使用更小的免疫节点比例值,以较小的免疫代价有效地保护网络,控制病毒的传播。 4 结束语 复杂网络的免疫策略研究对抑制病毒传播具有重点现实意义,本文先对比分析了几种经典的免疫策略,基于图覆盖免疫策略,引入模拟退火的思想,提出一种改进方法,结合交互式邮件传播模型,在真实的网络数据上设计了多组实验,从免疫效率和免疫代价的角度对比了原方法和本文改进的方法,发现改进的方法在一些社团结构明显的网络中具有更好的效果,从而验证了本文方法的有效性。未来的研究方向是针对不同的网络,如何选取图覆盖距离d的取值。 参考文献(References): [1] 阮中远.复杂网络上的流行病传播[J].中国科学:物理学力学天文学,2020.1. [2] 葛新,赵海,张君.基于熟人免疫的复杂网络免疫策略[J].计算机科学,2011.38(11):83-86 [3] 李向华,王欣,高超.复杂网络免疫策略分析[J].吉林大学学报(理学版),2013.3:444-452 [4] Cohen J E. Infectious Diseases of Humans: Dynamics andControl[J].JAMA The Journal of the American Medical Association,1992.268(23):3381 [5] Pastor-Satorras R, Vespignani A. Immunization ofcomplex networks.[J].Physical Review E,2002.65(3):106-126 [6] Cohen R, Havlin S, Ben-Avraham D. Efficient Immuniza-tion Strategies for Computer Networksand Populations[J].Phys Rev Lett,2003.91(24)12343-12343 [7] P E, J G, Y M, et al. Distance-d covering problems inscale-free networks with degreecorrelations[J].Physical Review E,2005.71(3):142-154 [8] Gao C,Liu J, Zhong N.Network Immunization withDistributed Autonomy-Oriented Entities[J]. IEEE Transactions on Parallel & Distributed Systems,2011.22(7):1222-1229 [9] Metropolis N , Rosenbluth A W , Rosenbluth M N, et al.Equation of State Calculations by Fast Computing Machines[J].The Journal of Chemical Physics,2004.21. [10] Jinna Ma, Yong Xiao, Hailing Xiong. An Improved AOC-Based Immunization Strategy Based on Simulated Annealing[J]. Journal of Computational Information Systems,2015.11(8): 2915-292 [11] Newman M E. Finding community structure in networksusing the eigenvectors of matrices[J]. Physical Review E Statistical Nonlinear & Soft Matter Physics,2006.74(3 Pt 2):92-100 [12] Zou C C, Towsley D, Gong W. Modeling and SimulationStudy of the Propagation and Defense of Internet Email Worm[J]. IEEE Transactions on Dependable and Secure Computing,2007.
