差异六面体网格模型间数据映射传递研究
2021-06-11胡广旭苗玉刚巩庆涛
刘 安,胡广旭,苗玉刚,巩庆涛
(1.哈尔滨商业大学机械系,黑龙江哈尔滨 150028;2.哈尔滨工程大学船舶工程学院,黑龙江哈尔滨 150001;3.鲁东大学蔚山船舶与海洋学院,山东烟台 264025)
近些年来,由于制造行业对智能制造与数值模拟技术的广泛认可,制造工艺链模拟技术也随之诞生。制造工艺链模拟技术是工艺模拟技术向多工序制造流程的延伸。随着工艺模拟研究的逐渐深入,采用多工艺制造的复杂零部件在不同工艺下的物理化学作用以及相互影响,渐渐受到工艺研究者的重视。欧洲先进制造领域研究者首先探索了制造工艺链模拟技术的相关研究。针对汽车结构制造优化问题,Papadakis L 等基于有限元方法开展了车体薄板结构冲压、焊接以及强度与碰撞计算的连续模拟,系统地分析了各工艺环节对结构制造最终质量的影响,进而全面协调各工艺环节进行整体优化,提高了产品的综合制造性[1]。Alexander Govik,Zaeh 等进一步开展了轻质合金的成形与焊接制造工艺链模拟研究[2-3]。在此基础上,为了保证工艺模拟数据传递,Afazov 开发了用于不同有限元计算软件之间的数据格式转换系统FEDES[4],并实现航空发动机圆盘组件的制造工艺链模拟,以保证应力应变数据在不同制造工艺模型间的继承与传递,进而实现了热处理、机械加工、喷丸处理等多种工序的制造工艺链模拟[5]。然而,尽管上述制造工艺链模拟技术可以“透视”整个制造过程,但实现制造工艺链模拟需有效地将有限元模拟数据在不同工艺模型间进行映射与传递,Afazov 相关程序代码尚未公开和商业化,限制这项技术进一步普及应用。因此,国内连续模拟仍处于单工艺连续模拟阶段,主要用于板料塑性成形工艺优化研究[6-7]。其中限制这项技术普及应用的关键问题是不同工艺模拟间的数据映射与传递技术,尤其是采用形函数法实现差异六面体网格间数据传递时,需求解非线性方程组,涉及迭代循环计算,计算数据量大,限制了该项技术的普及应用[8]。因此,文中将在前期研究基础上[9-10],通过直接计算方法代替迭代循环计算,实现了差异六面体网格的有效数据映射,并开发其用户程序。
1 差异网格数据映射技术
开展制造工艺链模拟时,为了保证模拟物理数据在不同工艺阶段数值模型的连续性,需将前道工序的模拟结果数据传递至后道工序的模型中。如果前后工序采用不同网格模型,还需将模拟结果数据映射至后道工序网格模型对应网格节点。常用差异网格间的映射插值技术有最近点法、点场距离法、单元距离法及形函数法[4]。其中,形函数法符合有限元网格原理,传递精度最高。该方法利用有限元单元形函数将单元节点的结果数据插值获得单元内任意位置点的结果数据。
如式(1)所示,其中Dp为单元内任意点P的结果数据值(应力、应变或位移)。

Di为单元节点上的结果数据值,ηi为Di相应的形函数参量。
计算8 节点的3D 六面体网格内任意点P的数据值时,其形函数如式(2)[4]。
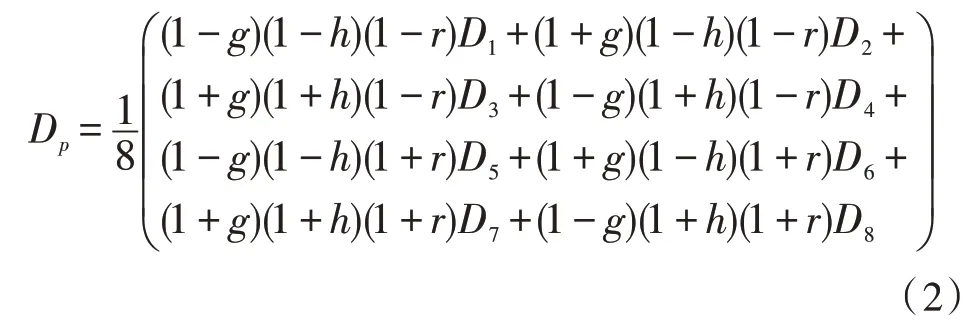
预求解六面体网格单元内任意点P对应映射局部坐标点(g,h,r)位置时,需求解式(3)的非线性方程组[4]。

此时计算式(3)时,需采用牛顿拉夫森进行循环迭代计算,且计算的精度取决于收敛精度。但采用上述方法实现三维六面体网格的差异网格数据传递时,求解局部坐标点(g,h,r)位置增加了网格传递循环计算量。
2 形函数法有限元数据传递算法流程
如图1 所示网格模型A 的节点数据传递至模型B 时,其算法流程为:
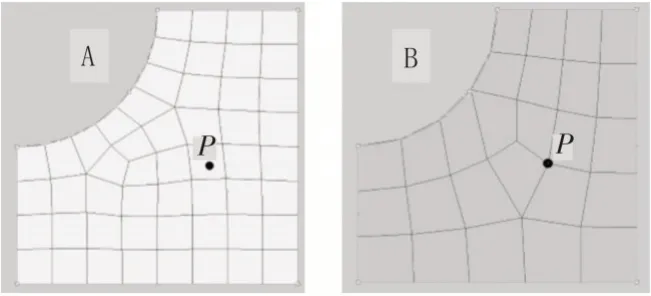
图1 数据映射的差异网格
1)在模型B 中循环获取任意节点的全局坐标值,即为P(x,y,z);
2)查找P(x,y,z)点在模型A 中所在单元EAi;
3)获取单元EAi的节点坐标数据Nj(x,y,z);
4)基于单元形函数,求解非线性方程组,如式(3),获得P(x,y,z)点的局部坐标映射值P(g,h,r);
5)在模型A 的模拟结果数据(应力、应变、温度等)中查找单元EAi的节点或积分点结果数据;
6)采用形函数插值法,如式(2),通过单元EAi的节点模拟数据,计算获取P(g,h,r)的插值映射值DP;
7)步骤循环1)~6),直至获取模型B 中所有节点的模拟数据值,退出循环。
按照上述算法[11-13],实现差异网格数据传递时,算法总循环为模型B 的总数CNB,传递其每一个节点数据时,都要循环获取EAi,对于六面体网格为8节点,此时计算所需循环数为CEA×8;进行算法步骤4)时,求解非线性方程组进行牛顿拉夫森迭代时,仍需循环计算,循环数为nC,取决于迭代步长和收敛精度;获取模型A 指定单元EAi模拟结果数据时,仍需进行循环A 单元数次εCEA,ε表示当获取指定单元后剩余单元数无需循环的系数,0<ε<1,可近似为0.5。基于上述可知总算法循环数为式(4):

假设模型A 六面体网格数量为10 万,网格B 节点数量为7 万,假设牛顿拉夫森循环数平均为50 次,此时总循环数按上式计算为2.803 5×1012次,且在每个循环下都进行大量空间计算,因此网格数据传递计算时间较长。数据传递的算法中,针对模型A 与B 的循环是不可避免的,因此为提高数据传递效率,本研究预实现步骤4)的简化直接计算,进而使nC值为1 次,从总循环数将降为5.95×1010。
3 六面体网格分解直接计算法
数据传递算法步骤4)计算主要实现单元内P点对应的局部坐标系值P(g,h,r)。该局部坐标系是用于定义六面体网格形函数建立,如图2 所示为局部坐标系定义[10,14-16]。该局部坐标系内,单元平面上局部坐标系值分别为-1≤g,h,r≤1。计算中,只要得到实际网格内任意点P(g,h,r)对应的局部坐标系点P(g,h,r)即可实现形函数方法映射。

图2 六面体单元及局部坐标
为了避免求解式(3)非线性方程组,分解的比例系数法获取P(g,h,r)值。首先进行如图3 所示的单元分解,点O(xO,yO,zO)为当前单元中心点,即为:

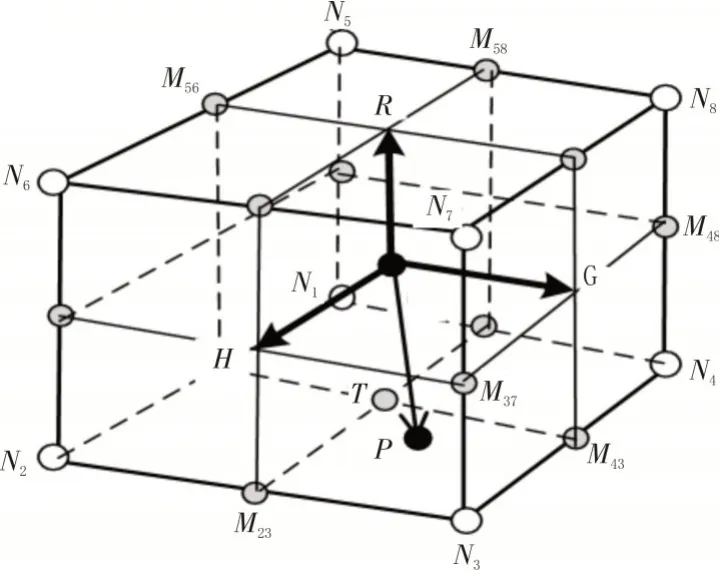
图3 单元分解示意图
构建G(xg,yg,zg),H(xh,yh,zh),R(xr,yr,zr),形成确定向量3 个方向向量以及面GOH,面HOR,面GOR,从而将单元划分为8 个子域空间。根据向量与面GOH法向量nGOR的夹角θnGOR值可以判断P点位于面GOR的正方向或负方向。


表1 P点子域判断规则
根据P点所在子域位置,进一步计算P(g,h,r)。按照图3 所示,此时,P点位于子域六面体Esub{O,H,M37,G,T,M23,N3,M43} 内。由于实际六面体网格为非理想等边六面体,此时计算P点局部坐标值(g,h,r)时,g不仅仅是沿的投影,还需协调考虑相关向量。此时,为了近似求解(g,h,r),该研究将的向量和平均值近似视为理想六面体的方向值,即为,如式(7)所示。

因此可以得到近似局部坐标系值如式(8)所示。

同理可得:
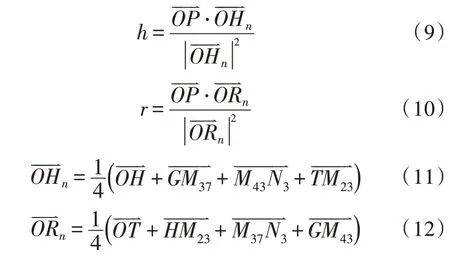
基于上述计算,即可获得单元内任意点P对应的局部坐标系映射值(g,h,r),实现了直接计算代替了迭代计算。
4 数据传递实例及分析
基于VC 对话框程序设计了用于网格数据传递的用户界面,如图4 所示。利用软件用户界面可以通过简单操作实现网格数据映射传递。具体流程如下,首先读取所需映射计算的A 与B 网格数据,然后读取A 网格的模拟结果数据,进而在程序中建立映射所需的网格与模拟数据相关的数组与类信息,最后点击“开始数据映射计算”按钮实现数据映射计算并监控运算进度。
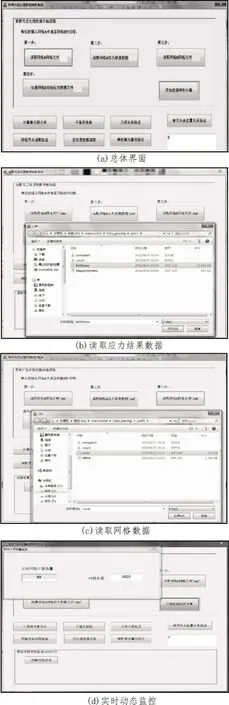
图4 软件用户界面
如图5 和图6 所示分别为将孔板与T 型焊接结构的细网格A 模拟数据传递至粗网格B。由云图结果可知,两种结构网格A 与网格B 的应力分布基本一致,由表2 数据可知,孔板结构差异网格数比为ηk=12.7,而T 型焊接件的差异网格数比为ηt=62.6 。由图7 和图8 所示的Mise 应力曲线对比可知,对比范围内数据传递获得粗网格的应力值基本与细网格的值一致,仅在结构边缘附近,由于网格尺寸差距,传递精度稍低,而在大部分位置传递数据基本与源数据一致,说明该研究采用直接计算法获取局部坐标映射点(g,h,r)是有效的。

图5 孔板结构Mise应力云图

图6 T型焊接结构Mise应力云图
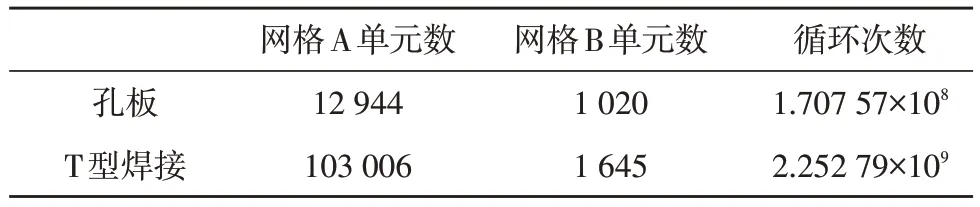
表2 网格数据传递信息

图7 T型结构背侧Mise应力随纵向焊接路径
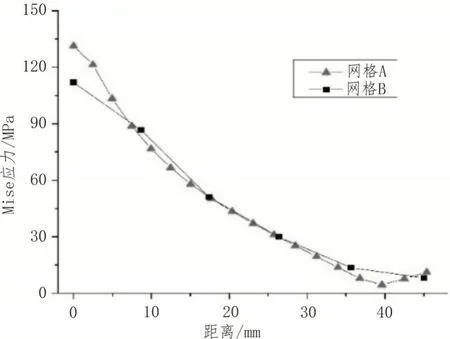
图8 孔板中心至边缘不同距离的Mise应力曲线
5 结论
基于对单元形函数分析,设计并开发了实现差异六面体网格间模拟数据传递的程序,并成功实现了孔板与T 型焊构件由粗网格向细网格的模拟数据传递,对比数据传递前后结果可知,其应力值传递结果数据与源结果模拟数据基本一致,且其传递精度与差异网格的网格数比值无关。与此同时,在差异六面体网格数据映射计算过程中,为了避免迭代循环计算单元内任意点的映射局部坐标值,提出了单元分解直接计算代替迭代求解计算方法,从而显著减少了网格数据传递的程序循环次数,提高了差异六面体网格间数据传递技术的可用性。
