基于ECG和HRV特征提取的情绪状态分析

郭景诗，乔晓艳

(山西大学 物理电子工程学院，山西 太原 030006)

情感在人们日常生活中发挥着非常重要的作用，是决定认知、 沟通和决策能力的关键因素. 情绪是情感的具体表现，利用机器分析和识别情绪是学者们一直追求的研究目标. 心电(ECG)是心脏每一个心动周期所产生的电活动变化，心电相邻心拍中R-R间期的变化称为心率变异性(HRV)，ECG信号和HRV信号可以直观地反映心脏活动，与自主神经系统有着密切关系，不同情绪状态有特定的自主神经反应模式，因而，ECG和HRV可以反映人体情绪变化[1]. 目前，国内外采用ECG和HRV信号进行情绪识别研究取得了一定进展. 如易慧、 陈瑞娟、 邓光华等[2]提取了ECG信号的时域特征和频域特征参数，并用支持向量机算法实现了情绪的分类，对于不同情绪的识别精度达到60%～75%； Nardell[3]等提取了HRV信号的时域、 频域特征、 近似熵、 去趋势波动分析(DFA)和滞后庞加莱图(LPP)特征参数，使用二次判别分类器进行情绪的分类识别，达到84%的正确率； Yu等[4]提取了HRV信号的11种时域特征、 6种频域特征和庞加莱图特征，采用遗传算法进行特征选择后，利用支持向量机进行情绪的4分类，最后得到了90%的平均分类正确率. 但是，用ECG和HRV信号进行情绪识别提取特征过多，其特征对不同情绪状态之间的特异性关系尚不明确，有效性也有待进一步探讨研究. 此外，心电和心率变异的非线性特征在情绪识别和分析中研究的不充分，而情绪的表现很复杂，时频非线性特征更容易描述情绪的复杂性和动态特性. 通过提取较多信号特征量，再进行特征优化选择，不利于情绪状态实时分析，特别是针对可穿戴设备动态监测情绪的实际应用，需要获得与情绪密切相关、 有特异性关系的少量生理特征. 因此，本文通过小波分解提取小波系数模极大极小值和过零点，充分利用小波变换对突变点检测的有效性和准确性，实现心电R波精确定位，获得准确反应情绪的HRV特征信号. 然后，分别提取ECG和HRV信号时域、 频域和时频非线性特征，在统计分析ECG、 HRV情感特征的基础上，旨在寻找到差异最显著的生理信号特征，为利用心电信号进行实时动态情绪识别提供有力支持.

1 情感生理数据库和情感模型

1.1 情感生理数据库

德国 Augsburg 大学 HCM 实验室的情感生理数据库是最简单也最为常用的数据库. 它采用4种不同风格的音乐作为情感诱发素材，在25 d内连续采集单一受试者4种离散情感状态： 高兴(joy)、 愤怒(anger)、 悲伤(sadness)和愉悦(pleasure)的生理信号，包括心电、 肌电、 皮肤电以及呼吸. 每种数据的长度是2 min，其中，心电的采样频率为256 Hz，心电信号含有100(25×4)个数据样本，4种情绪状态各25个心电数据样本，该数据库是目前对单人进行情感研究最常用的数据库. 为了更有效地处理数据，本文以60 s为时间间隔将每个ECG信号分成2段，得到200(50×4)个心电样本，每种情感状态包含50个ECG，选取30个组成ECG数据样本集； 然后，从原始ECG信号以及ECG组合信号中，经过HRV特征提取，截取HRV序列长度为130个采样点，对4种情绪状态各选取30组HRV特征信号，组成HRV数据样本集. 该ECG和HRV数据样本集用于后续的特征提取和情绪状态分析.

1.2 情感模型

对于情绪的表征方式，目前在学术界达成明确共识的主要有离散情感模型和连续情感模型两类. 离散模型认为，所有的情绪是由若干基本情绪或对基本情绪组合而构成的,如Plutchik[5]等人提出了8种基本情绪： 愤怒，恐惧，期待，悲伤，厌恶，惊讶，接受和欢乐. 除此之外，其他情绪都可以通过这些基本情绪的组合形成，如失望可由悲伤和惊讶组合而成. 连续情感模型是用多维连续矢量表征情绪状态，例如把情绪映射到效价(valence)、 唤醒度(arousal)、 优势度(dominance)3个维度上的V-A-D三维模型. 可以根据研究需求，对模型的表征空间进行划分，维度空间不同区域表示不同情绪类型： 如高兴可认为是一种高效价、 高唤醒程度的情绪，而愤怒则对应低效价、 高唤醒程度的情绪. 本文所采用的情感生理数据库是基于离散情感模型.

2 心电R波检测与HRV特征提取

2.1 心电信号预处理

图1 是一段典型的ECG信号波形，主要由P波、 T波和QRS波群构成.

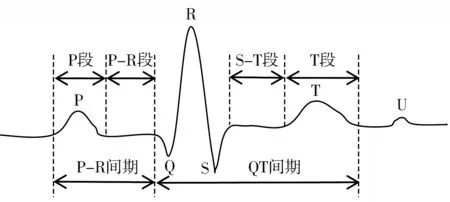
图1 心电图波形Fig.1 ECG waveform

人体的ECG信号频率低且非常微弱，一般地，其幅值在5 mV以下，主要频率范围为0.051 Hz. 受周围环境和人工测量的影响，ECG信号通常存在3种干扰类型： 肌电(EMG)干扰、 基线漂移和工频干扰. 结合Augsburg数据库的心电数据和本研究只需提取心电R波的实际情况，本文对ECG信号进行滤除肌电干扰的预处理.

由于肌电信号的主要频带范围为100 Hz～300 Hz，主要的能量集中在150 Hz. 论文采用5阶Butterworth数字低通滤波器滤除肌电干扰[6].

图2 所示是滤除肌电干扰前、 后的ECG信号(仅显示5 s时长)，可以看出，高频的肌电干扰得到有效滤除.

图2 原始ECG信号和预处理后的ECG信号Fig.2 Original ECG signal and pre-processed ECG signal

2.2 小波变换的R波检测

获得HRV特征信号首先需要提取ECG信号的R波，根据小波变换(WT)检测信号突变点的方法，选取与ECG信号形态近似的mexh小波作为小波母函数，提取ECG信号的R波. 具体算法过程如下：

1) 确定WT系数： 将预处理后的ECG信号进行6层mexh小波分解，得到WT系数矩阵wsig.

2) 检测极大极小值对： 在小波变换域上，首先找到所有峰值点并放入sigmax矩阵中； 将矩阵sigmax中的数据进行排序，获得前8个极大值点和后50个极小值点的两个均值后，以两者之间差值的25%～55%(根据不同数据幅值的差异来进行灵活调整)作为阈值，检测整条数据的极大极小值点来获得极大极小值对(Max-Min Pairs)[7].

3) 初步确定R波峰值点： 求取Max-Min Pairs的零交叉点，记此点的位置点为rvalue(i)，初步确定rvalue(i)是R波峰值点，以此类推求取整条ECG数据的R波波峰.

4) 排除误检漏检： 计算相邻极值点之间的时间间隔Rt，若Rt小于100 ms或大于300 ms，则删掉幅值较小的一个，以获取新的R波峰值点矩阵rvalue.

5) 对原始信号进行精确校准： 在rvalue(i)之前和之后取5个采样点，在这10个采样点中找到最大值，并将该点重新确定为R波的峰值.

由此提取得到的心电R波波峰(圆点)如图3 所示，R波的检测精度为100%.

图3 小波变换提取的R波波峰Fig.3 R wave peak extracted by wavelet transform

2.3 HRV特征信号提取

HRV信号用来反映心脏在每个跳动节拍内存在的周期差异变化现象，HRV的大小反映自主神经系统的交感神经活性与迷走神经活性及平衡的协调关系，提供自主神经系统和压力状态的信息，HRV能一定程度上表征情绪变化. 论文通过计算心电R波波峰对应时间的一阶差分，得到HRV特征信号，计算公式为

HRV(i)=R(i+1)-R(i),

(1)

式中：i为R波峰位置对应的采样点.

图4 为四种情绪状态的HRV信号时域图，横坐标为心电R波波峰位置对应的采样点，纵坐标代表每种情绪的HRV值.

图4 4种情绪状态HRV信号波形图Fig.4 HRV signal of different emotions

由图4 中的HRV信号可以看出，不同情绪状态下的HRV信号波形存在明显差异，可通过分析HRV信号的各种特征来判断被试者的情绪状态.

2.4 小波熵

小波熵(WE)是结合小波变换与信息熵理论的一种特征分析方法，可以反映信号的复杂性并获得非线性动态时频特征信息，其值越大，说明复杂性越高. 计算WE的过程如下：

2) 小波系数能量分布表示为Pi=Ei/E；

3) 计算小波熵WE(P)=-∑Piln(Pi).

3 ECG和HRV信号情感特征分析

提取ECG，HRV信号的时域、 频域、 时频非线性特征，进一步分析不同情绪状态的ECG，HRV特征差异.

3.1 时域特征

3.1.1 ECG时域特征

不同情绪的ECG信号在时域上存在差异，本文采用标准差来度量每一种不同情绪ECG信号的离散程度，标准差计算公式为

(2)

分别计算4种情绪状态ECG信号的标准差，图5 所示为其归一化后标准差值的柱状图，表 1 为其差异性分析结果，其中SS为偏差平方和，df为自由度，MS为均方值；F为检验统计量，等于组间MS与组内MS的比值，Fcrit是检验临界值；P-value是显著性差异水平. 在F>Fcrit时，若P-value<0.05，表明特征在显著水平α上差异显著，当P-value<0.01时，表明特征在显著水平α上差异极显著.

表 1 ECG信号标准差的方差分析Tab.1 The variance analysis of standard deviation for ECG signals

图5 不同情绪下的ECG信号标准差柱状图Fig.5 The histogram of standard deviations for ECG signalsunderfour emotions

3.1.2 HRV时域特征

HRV的时域分析是对提取到的RR时间间隔进行数学运算，可以评估自主神经系统对心率变化的调节情况. 本文选用的时域评价指标为：

1)SDNN： RR间期的标准差，单位为ms.

2)SDSD： 相邻RR间期时间长度之差的标准差，单位为ms.

对4种情绪状态HRV信号的SDNN，SDSD特征进行统计分析，如图6 为其归一化后SDNN，SDSD的柱状图，表2为其差异性分析结果.

表 2 HRV信号时域特征的方差分析Tab.2 The variance analysis of time-domain featuresfor HRV signal

图6 不同情绪下的HRV信号时域特征柱状图Fig.6 The histogram of time-domain features forHRV signals under four emotions

3.1.3 时域特征分析

从图5 的柱状图可以看出，不同情绪下ECG信号的标准差存在明显差异. 其中，愤怒和悲伤的标准差值较高兴和愉悦的标准差值更高，表明愤怒和悲伤情绪的ECG信号与其平均值的离散程度大，ECG信号波动更大. 从图6中的柱状图可以看出，不同情绪下HRV信号的SDNN，SDSD特征存在明显差异. 其中，高兴和悲伤的SDNN值较愤怒和愉悦的SDNN值更大，表明高兴和悲伤情绪的心率总体变化较大； 负性情绪(愤怒和悲伤)的SDSD值较正性情绪(愉悦和高兴)的SDSD值大，表明负性情绪的心率变化快的成分更多.

从表 1、 表 2 的差异性分析结果可以看出，ECG信号标准差的方差分析P-value=0.049<0.05，表明4种情绪下ECG标准差时域特征差异显著； HRV信号SDNN特征的方差分析P-value=0.013 4<0.05，表明4种情绪下HRV的SDNN特征值差异显著，SDSD特征的方差分析P-value=0.004 66<0.01，表明4种情绪下HRV的SDSD特征值差异极显著. 同时，HRV信号时域特征的P-value明显要比ECG信号时域 特征的P-value更小，表明4种情绪下HRV信号时域特征比ECG信号时域特征差异性更显著.

3.2 频域特征

3.2.1 ECG频域特征

对信号进行功率谱分析可以提取不同情绪状态ECG信号频域特征. 基于自回归(AR)模型的现代谱估计，相比经典周期图谱估计得到的频谱曲线更平滑，谱峰的中心频率容易识别，对时间序列长度要求更短[8]. 本文采用pburg法AR模型功率谱估计，模型阶数设置为8，计算4种情绪状态ECG信号的功率谱密度. 为了能够定量分析，对得到的功率谱密度进行标准差计算，得到4种情绪状态ECG信号功率谱密度的标准差. 图7 为归一化后的功率谱密度标准差柱状图，其差异性分析结果如表 3 所示.

表 3 ECG信号功率谱密度标准差的方差分析Tab.3 The variance analysis of PSD standard deviationfor ECG signal

图7 不同情绪下ECG信号功率谱密度标准差柱状图

3.2.2 HRV频域特征

正常人基础状态下HRV频谱的频率范围为0 Hz～0.4 Hz，其中，0.003 Hz～0.04 Hz为甚低频段(VLF)，0.04 Hz～0.15 Hz 为低频段(LF)，0.15 Hz～0.4 Hz 为高频段(HF). 对HRV信号进行频域分析时，发现频谱的不同频段对应着不同神经电活动，如低频功率主要反映交感神经的活动，高频功率反映迷走神经的活动[9]. 本文提取了4种情绪状态下HRV信号频谱的总功率TP、 高频功率PHF、 低频功率PLF、 低频功率与高频功率之比LF/HF4个频域特征，绘制了如图8 所示的归一化后HRV频域特征的柱状图，并进行差异性分析，结果如表 4 所示.

表 4 HRV信号频域特征的方差分析Tab.4 Variance analysis of frequency domain features for HRV signals

图8 不同情绪下HRV信号频域特征柱状图Fig.8 The histogram of frequency domain features forHRV signal under four emotions

3.2.3 频域特征分析

从图7 柱状图可以看出，不同情绪下ECG信号的功率谱密度存在明显差异. 其中，愤怒和悲伤的功率谱密度的标准差值较高兴和愉悦的更高，表明愤怒和悲伤情绪的ECG信号功率谱密度值波动更大.

从图8柱状图可以看出，不同情绪下HRV信号的TP，PHF，PLF，LF/HF特征皆存在明显差异. 其中，悲伤和愉悦的TP值较高兴和愤怒的TP值更大，表明悲伤和愉悦情绪的自主神经系统整体的活性较大； 愤怒和悲伤的高频功率PHF值较愉悦和高兴的PHF值大，表明愤怒和悲伤情绪下个体的迷走神经对心率的调节更大； 高兴和悲伤的低频功率PLF值较愉悦和愤怒的PLF值大，表明高兴和悲伤情绪下个体的交感神经和迷走神经对心率的共同调节更大； 高兴和愤怒的LF/HF值较愉悦和悲伤的LF/HF值更大，表明高兴和愤怒情绪下自主神经系统的平衡状态更好.

从表 3、 表 4 的差异性分析结果可以看出，ECG信号的功率谱密度标准差的方差分析P-value=0.013 4<0.05，表明4种情绪下ECG功率谱密度差异显著； HRV信号的TP，PHF，PLF，LF/HF特征的方差分析P-value值皆小于0.01，表明4种情绪下HRV的TP，PHF，PLF，LF/HF特征值差异极显著. 同时，HRV信号频域特征的P-value值明显小于ECG信号频域特征的P-value值，表明4种情绪状态HRV信号频域特征相比ECG信号频域特征的差异性更显著.

3.3 时频非线性特征

3.3.1 ECG小波熵特征

在不同情绪状态下，ECG和HRV信号的幅度不同，而且不同情绪状态的ECG信号小波分解后各尺度对应频带上的能量也不相同，小波熵可以反映信号不同尺度小波系数能量分布的非线性复杂程度，所以采用小波熵对不同情绪状态及具有非平稳特性的ECG和HRV信号进行分析是可行的[10]. Kutlu和Kuntalp[11]用不同小波基对ECG信号分解结果进行了对比，指出db6小波基的平滑特性使得其分析ECG信号时可得到最好的特征集，更加适合用于心电信号的处理. 本文选取db6小波基函数对ECG信号进行3层分解，提取4种情绪状态下ECG信号的小波熵特征，绘制如图9 所示的小波熵柱状图，并进行情绪状态的差异性分析，结果如表 5 所示.

图9 不同情绪下ECG信号的小波熵柱状图Fig.9 WE histogram of ECG signal under four emotions

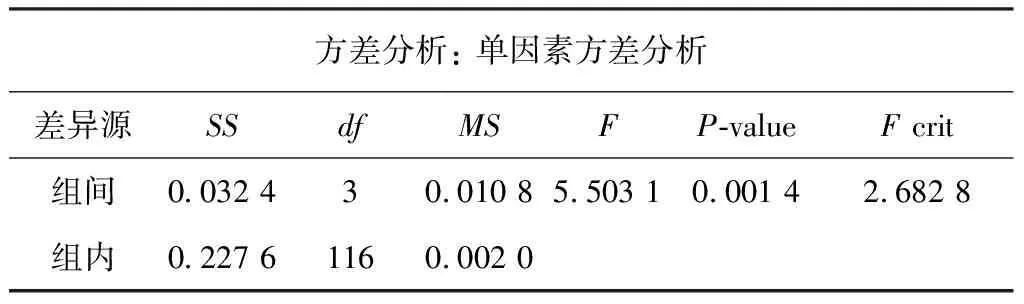
表 5 4种情绪状态的ECG信号小波熵方差分析Tab.5 WE variance analysis for ECG signal under four emotions

3.3.2 HRV小波熵特征

对HRV信号小波基函数的选取根据自相似原则[12]，即若小波基函数与信号具有相似性，则小波变换后的能量比较集中，可减少计算量，本文选取db10小波基函数对HRV信号进行3层小波分解. 然后，提取4种情绪下HRV信号的小波熵特征，绘制如图10 所示的HRV小波熵柱状图，并进行情绪状态差异性分析，结果如表 6 所示.

表 6 4种情绪状态的HRV信号小波熵方差分析Tab.6 WE variance analysis for HRV signal under four emotions

图10 不同情绪下HRV信号小波熵柱状图

3.3.3 时频非线性特征分析

从图9 柱状图可以看出，不同情绪下ECG信号的小波熵存在明显差异. 其中，高兴和愉悦的小波熵值较愤怒和悲伤的小波熵值更高，表明高兴和愉悦情绪的ECG信号复杂性和动态不确定性更高. 从图10 柱状图可以看出，不同情绪下HRV信号的小波熵特征存在明显差异. 其中，愤怒和悲伤的小波熵值相比高兴和愉悦情绪的小波熵值更大，表明对于愤怒和悲伤情绪，HRV特征的复杂性和动态不确定性更高.

从表 5、 表 6 的差异性分析结果可以看出，ECG信号的小波熵方差分析P-value=0.001 4<0.01，HRV信号的小波熵特征方差分析P-value=2.483 01E-05<0.01，表明4种情绪下ECG，HRV信号的小波熵特征差异极显著. 同时，HRV信号小波熵特征的P-value值明显要比ECG信号小波熵特征的P-value值更小，表明4种情绪状态HRV信号小波熵特征相比ECG信号差异性更显著.

4 结 语

本文采用小波变换检测奇异点的方法，通过提取ECG信号的模极值点和过零点，准确定位R波并计算其波峰的一阶差分，得到HRV特征信号. 然后提取ECG信号和HRV信号在时域、 频域、 时频非线性特征，实现对高兴、 悲伤、 愤怒、 愉悦4种情绪状态的特征分析. 结果表明，使用HRV特征对情绪进行分析识别相比直接采用ECG特征更准确、 差异性更显著，而且小波熵、 HRV的频谱总功率两个生理特征量对应的情绪状态差异显著性最高，故而在可穿戴设备情绪动态监测分析中可以采用，该研究为情绪的机器识别提供了良好的借鉴.