锥形聚音器声传播特性研究
2021-06-11刘康驰
高 斌,杨 录,张 梁,田 力,刘康驰
(1. 中北大学 信息与通信工程学院,山西 太原 030051;2. 中北大学 电子测试国家重点实验室,山西 太原 030051)
0 引 言
聚音器是一种提高声学系统性能的有效装置,如图1 所示,通过可变截面面积的声导管,将声信号集中放大,实现高效率声电转换,在设备故障检测中应用广泛[1-3].
图1 聚音器应用原理图Fig.1 Schematic diagram of the sound concentrator
针对聚音器中声传播问题的求解,韦伯斯特提出声波在圆截面导管中近似平面波传播,将导管中的三维波动方程转换为一维,简化了对聚音器模型的求解[4-6]; Tamanoi等人针对机器故障振动信号,设计了一种声音收集罩,实现准确检测并诊断旋转机械中微小声音信号[7]; 羽田野甫等人设计了一种旋转抛物面声音收集器,将设备振动信号收集起来,便于信号分析[8]; Kleeman针对声纳环接收问题设计了用于缩小声发射器垂直波束宽度的抛物线反射器,并提出抛物线反射器声环境的仿真模型[9]; 对于指数型、 圆锥型、 抛物线型、 级联型、 正弦型等多种形状导管中声传播问题,Putland采用韦伯斯特理论进行分析[10],但针对上述结构未得到具体声压解析式; Olson设计了抛物面聚音器,通对低频声音信号有效采集,并获得一定增益,给出了两端声压比解析式[11]; 孙生生等人对锥形管内的声场作了简单的理论分析,得出渐缩锥形管具有增强压比的功能[12], 但没有计算渐缩锥形管的声损耗; 项端祈比较了几种消声器常用公式的计算值,但同样没有讨论针对锥形管声损耗[13].
目前,针对聚音器对声损耗影响的研究较少. 鉴于此,本文基于韦伯斯特理论和别洛夫声损耗原理,建立锥形聚音器声传播与声衰减理论模型,利用有限元软件对锥形聚音器中的声传播进行数值模拟.
1 聚音器理论
声波在聚音器中的传播规律满足波动方程,在笛卡尔坐标系中可以表示为

(1)
式中:φ为速度势;c为空气中声速,由于方程在变截面声导管中的求解较为复杂,韦伯斯特[2]提出将方程(1)从三维简化为一维问题的解决方案:假设声能在垂直于变截面导管轴均匀分布,并且只考虑在轴向的运动,推导出韦伯斯特方程[14]

(2)
式中: 横截面积σ为x的函数,由文献[11]可得聚音器中声波动方程为
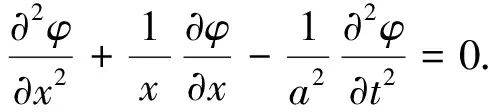
(3)
对式(3)进行求解可得速度势φ,该解可确定聚音器任何一点的声压值[11].
φ=[AJ0(Kx)+BY0(Kx)]eiωt,
(4)
式中:A,B为常系数;J0(Kx)为零阶贝塞尔函数;Y0(Kx)为零阶诺依曼函数.

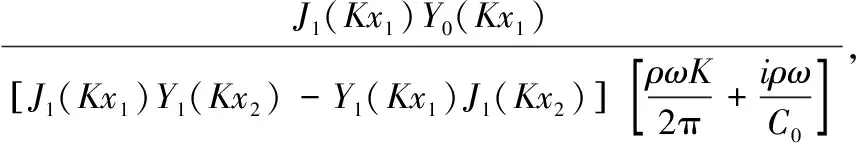
(5)
式中:J1(Kx),Y1(Kx)分别为一阶贝塞尔函数和一阶诺伊曼函数,ω=2πf为圆频率;K=2π/λ为波数;ρ为空气密度;σ1为大端面面积;R为大端面的开口半径;C0=4R为聚音器结构参数.
2 聚音器内壁声损耗
由文献[13,15]可知,对于直管中声衰减量

(6)
式中:L为气流通道断面的周长,单位为m;S为气流通道的截面面积,单位为m2;l为管道长度,单位为m;φ(α0)为消声系数,与材料吸声系数α0有关.
式(6)为直管中声衰减量计算公式,下面分析锥形管的声衰减量:在如图2 所示锥形管结构中,R1为大端半径,1/2锥形夹角θ=arctan(R1/m+n),声波入射角β=π/2-θ.

图2 聚音器结构示意图Fig.2 Schematic diagram of sound concentrator
内壁声反射系数Cr与材料声阻抗、 空气声阻抗、 声波入射方向有关,可以表示为

(7)
式中:z为聚音器外壳材料的声阻抗;ρ为空气密度;c为空气中声的传播速度. 通过式(7)声反射系数可求得内壁吸声系数

(8)
由式(8)推出聚音器内壁消声系数,其换算公式为
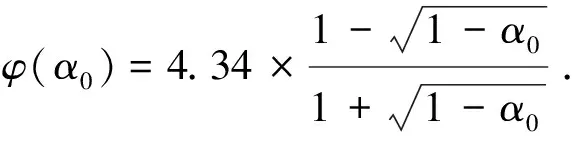
(9)
图3 中,取无穷小长度微元dx,锥形管可以等效为无数直管组成,对长度进行积分,通过式(10)可得,声信号从x1到x2的声衰减量为

图3 微元等效模型Fig.3 Microelement equivalent model

(10)
式中:x1和x2取大小端面中心点,锥型声导管斜率k=tanθ.
3 聚音器有限元模型及仿真分析
使用有限元分析软件建立如图4 所示聚音器结构,在大端面加载入射声波脉冲,求解小端声压值,大端与小端声压比值为聚音器声压放大倍数.

图4 聚音器尺寸示意图Fig.4 Schematic diagram of the size of the sound concentrator
根据文献[16,17],硬声场边界条件下声波全反射,不存在透射情况,即传播界面上没有声能的损耗. 鉴于此,本文将内壁设为硬声场边界,此条件下声传播没有损耗,所以聚音器声压放大倍数最大. 为进一步研究材料对聚音效果的影响,将上述结论作为理想情况,比较钢、 铝、 聚苯乙烯、 尼龙4种材料聚音器声传播特性.
硬声场边界下声压变化仿真求解:大端面加载f=40 kHz的正弦单周期脉冲超声信号. 信号表达式为
x(t)=5sin(2πft)[u(t)-u(t-Ts)],
(11)
式中:Ts=2.5e-5,单位为s. 物理场选择压力声学和固体力学,使用压力声学模块对聚音器内部的空气域进行分析,材料使用固体力学分析,使用声-结构边界将压力声学场和固体力学场进行耦合. 网格划分采用自由4面体网格,最大网格尺寸hmax为声波波长的1/5,最小网格尺寸为声波波长的1/6. 时间步长的选择受到稳定性条件的限制,为了保证计算收敛,选择时间步长为(1.25e-6) s. 由于仿真模拟超声波随时间的变化关系,研究选择瞬态. 仿真结果后处理中,绘制聚音器内部的声压剖面云图如图5 所示.
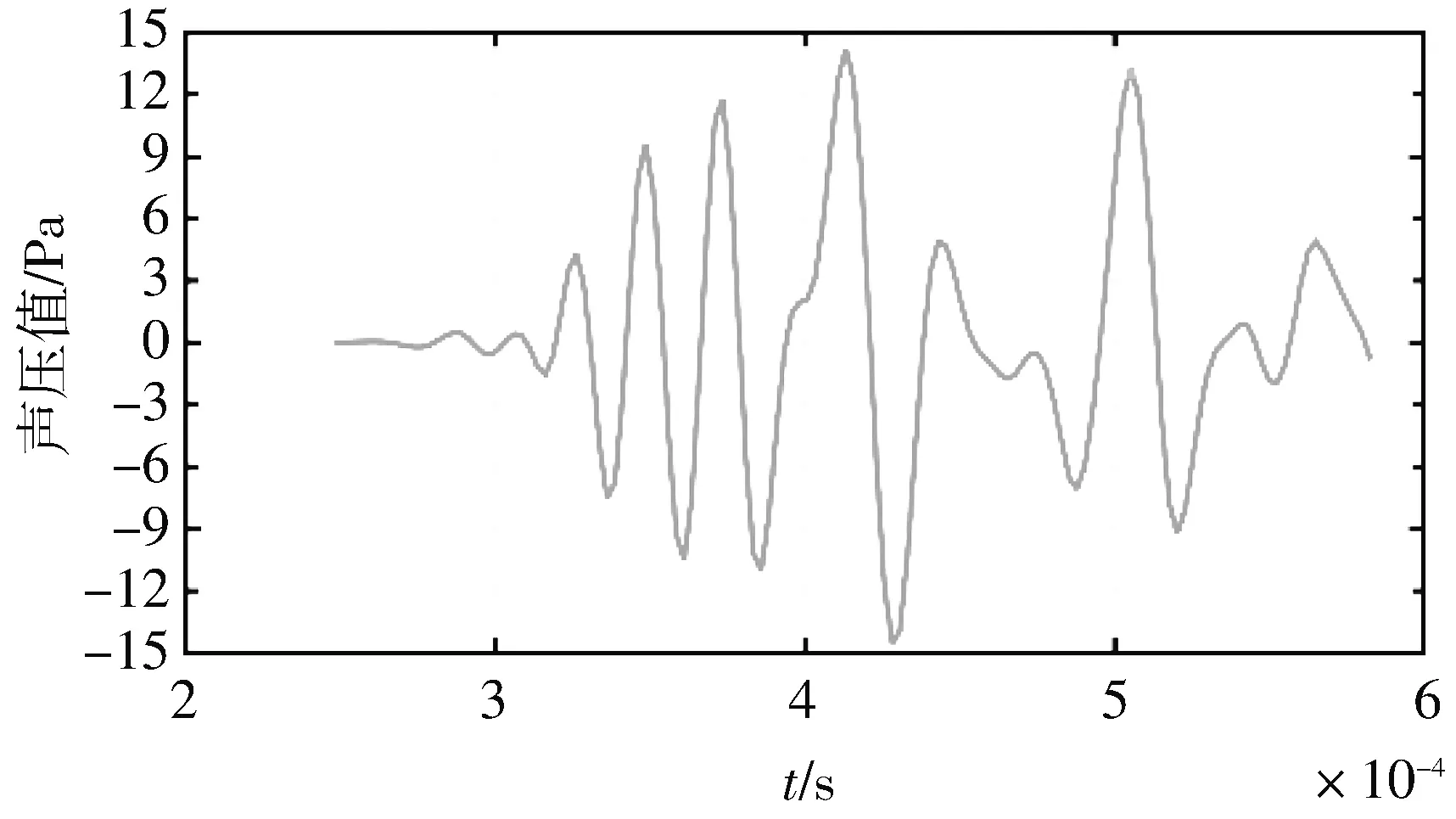
在剖面云图中接近上方的区域,声压值越高. 由图5(a) 中可得出,在大端面声压幅值最高6.83 Pa,声脉冲信号传播至小端时,如图5(b)所示,声压幅值最高为26.9 Pa. 进一步分析聚音器对声压的放大倍数,在大、 小端选取点(0,0,0)和(0,0,140.6)绘制声压点图,结果如图6 所示.
(a) 开始加载声脉冲的剖面声压云图

(b) 声脉冲传播到小端剖面声压图图5 聚音效果云图(材料壁为硬声场边界)Fig.5 Polyphonic effect Cloud map (the material wall is theboundary of hard sound field)
(a) 硬声场边界

(b) 钢材料

图6 硬声场边界入射脉冲与小端声压点图Fig.6 Hard sound field boundary incident pulse and small endsound pressure point diagram
图6 中左侧波形为聚音器大端面加载信号x(t)的声压点图,右侧波形为小端面声压点图. 声压幅值为4.762 Pa的信号经过聚音器到达小端时幅值变为14.19 Pa,声压幅值放大2.98倍,将此结果作为基准对不同材料声阻抗条件下声压放大倍数作数值分析.
为了定量计算材料内壁声阻抗对聚音效果的影响,将内壁由硬声场改为钢、 铝、 聚苯乙烯和尼龙的声阻抗条件,其他参数不变,对比4种不同材料下声压值的变化. 对聚音器进行声传播仿真,其内部声压剖面云图如图7 所示.
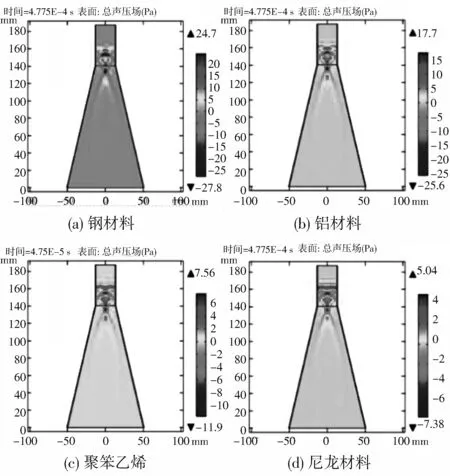
图7 4种材料聚音器小端剖面云图Fig.7 Small end profile cloud map of the soundconcentratorof four materials
从仿真结果可得出,锥形聚音器小端最大声压分别为24.7 Pa, 17.7 Pa, 7.58 Pa, 5.04 Pa,钢材料声压最大,尼龙材料声压最小. 将4种材料与硬声场边界条件下基准声压幅值进行对比,选取坐标点(0,0,140.6),绘制声压点图,结果如图8 所示.

(c) 铝材料

(d) 聚苯乙烯
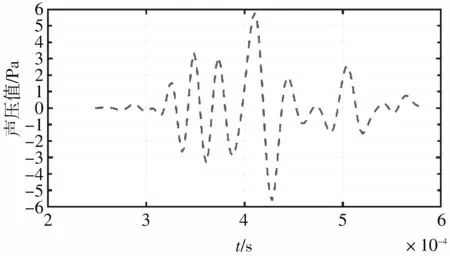
(e) 尼龙材料图8 硬声场边界与4种材料聚音器小端面声压对比图Fig.8 Hard sound field boundary and four kinds of material soundconcentrator sound pressure contrast diagram of small end face
图8 中,实线为小端在硬声场边界条件下无声损耗的声压点图,虚线为4种材料声阻抗条件声压点图. 计算可得钢、 铝、 聚苯乙烯、 尼龙4种材料小端声压幅值和声压放大倍数,如表 1 所示.

表 1 不同边界条件聚音器小端声压幅值和放大倍数Tab.1 Sound pressure amplitudes and amplification multiplesat the small end of the sound concentrator
从表1中可以得出,使用钢,铝,聚苯乙烯和尼龙作为聚音器外壳材料时,声波脉冲到达小端时的声压值、 放大倍数依次减小,表明上述4种材料对声的损耗依次增加.
分别计算内壁为硬声场条件和不同材料阻抗条件下小端声压级
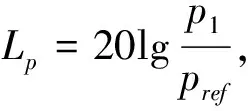
(12)
式中:p1为小端声压幅值;pref为基准参考声压,空气中取pref=2×10-5Pa.
由式(12)可求得硬声场边界下小端声压级Lp1与4种不同材料声阻抗条件下小端声压级Lp2,两者之差ΔLp即为声脉冲信号在内壁因透射而造成的声衰减量
ΔLp=Lp1-Lp2.
(13)
利用式(13)计算硬声场边界下声压变化并计算差值ΔLp即为仿真得到的聚音器内壁声损耗值,而理论值由式(10)得出,具体分析理论值和仿真值得到聚音器中声损耗机理. 因声损耗理论计算和仿真结果均与材料声阻抗密切相关,如下给出4种材料声阻抗下声损耗的理论和仿真对比,如表 2 所示.

表 2 4种聚音器材料声损耗理论值与仿真值对比Tab.2 Comparison of theoretical and simulated values of acousticlosses of four kinds ofsound concentrator
表 2 中,钢、 铝材料声阻抗较大,分别为4.6×106g/cm2·s和1.69×106g/cm2·s,聚音器中声损耗值较小,仿真值分别为0.527 8 dB和1.393 8 dB; 聚苯乙烯和尼龙的声阻抗较小,分别为0.246 7×106g/cm2·s和0.198×106g/cm2·s,声损耗值较大,仿真值分别为5.763 8 dB和7.792 9 dB. 从表 2 中可以得出,随着材料声阻抗的减小,聚音器内部的声损耗增大,仿真值符合理论计算值.
本节利用有限元仿真计算在不同材料下聚音器小端声压值,得出4种材料对声的损耗值,验证了仿真结果和锥形管声损耗理论的一致性.
4 结 论
聚音器作为声接收设备,声压放大倍数和声损耗是评价其性能优劣的重要指标. 本文利用有限元仿真软件定量计算钢、 铝、 聚苯乙烯、 尼龙4种材料聚音器性能参数. 仿真结果表明,材料声阻抗增大,聚音器内壁的声损耗减小; 声压放大倍数越高,聚音效果越好,与理论推导相符. 所得结果为研究锥形管中声传播与损耗机理提供了理论支撑,且对聚音器材料选择具有重要参考价值. 后续将考虑结构参数与聚音效果之间的相关性,寻找几何结构对聚音效果的最优解.
