综合考虑多目标、多资源约束及接力势的关键链缓冲区计算方法研究

2021-06-11聂相田

水力发电 2021年3期

聂相田，凌磊，苏博，王博

(1.华北水利水电大学水利学院，河南郑州 450046；2.水资源高效利用与保障工程河南省协同创新中心，河南郑州 450046；3.河南省水环境模拟与治理重点实验室，河南郑州 450046)

0 引言

关键链项目管理中，缓冲区大小的计算方法主要有剪切-粘贴法[1]和根方差法[2]。许多学者以根方差法为基础，提出了多种改进缓冲区设置方法，如Radovililsky[3]将成本因素考虑到缓冲区计算中，运用排队系统的优化方法，提出了单资源约束下缓冲区计算方法；张俊光等[4]提出了综合考虑多目标、多项目关键链缓冲区计算方法；徐小峰等[5]充分考虑项目工序安全工期等影响因素，提出了多因素扰动的缓冲区计算模型；王景桦等[6]将人为因素以及项目的制约因素融入缓冲区计算中，通过关键链项目管理对项目进度风险进行定量分析。Tukel[7]等考虑资源利用程度及项目复杂程度，提出了多资源约束下缓冲区计算方法；胡晨等[8]综合考虑了活动工期风险、资源影响系数和非关键链剩余缓冲等因素，提出了一种新的缓冲区设置方法。蒋红妍等[9]在文献[8]基础上考虑活动之间的信息流的传递与反馈作用对活动工期的影响，提出了信息综合影响系数的计算方法，改进了关键链缓冲区大小的计算方法。上述研究成果完善和改进了缓冲区大小的计算方法，但仍存在以下问题：①缓冲区大小计算时，没有考虑工序与工序之间存在的相互协作、交叉施工及资源共享的关系对后续节点持续时间的影响；②在确定工序安全时间时未综合考虑成本、质量及安全对工序工期的影响。针对以上局限性，本文提出了一种综合考虑项目多目标、多资源约束及接力势的缓冲区计算方法。

1 成本、质量、安全目标对工期的影响

1.1 成本对工期的影响

根据文献[10]中成本与工期关系确定工序直接成本与工期之间的关系如图1所示。

图1 工序直接成本—工期关系

假设工序持续时间与直接成本存在反曲函数关系，则工序直接成本与工期关系为

(1)

(2)

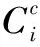
1.2 质量对工期的影响

根据文献[11]中质量与工期关系确定工序质量与工期关系图如图2所示。

图2 工序质量—工期关系

假设质量与持续时间之间存在着二次抛物线函数关系，则工序持续时间与工序质量关系为

(3)

(4)

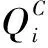
1.3 安全对工期的影响

根据文献[12]中安全与工期关系确定工序活动持续时间与安全水平存在一次函数关系为

(5)

式中，Si为工序i的安全水平指数，d；TiS为安全因素影响下工序i的持续时间；μi为工序i持续时间与Si之间的系数；TS为工序i的最短工期。

1.4 安全时间的确定

工序最可能的持续时间Zi为

Zi=max{TiC，TiQ，TiS}

(6)

工序i的安全时间STi为

(7)

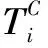
2 资源影响系数的确定

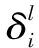
(8)

资源受限系数εl为

(9)

资源影响系数RIi[8]为

(10)

上述方法考虑各资源的受限程度以及各工序对资源需求强度的影响，资源影响系数越大，说明资源不能充分供应给该工序带来的影响越大，所需缓冲越大。

3 工序接力势的计算

定义1[14-16]：接力势是指在接力链网络中接力点的紧前工序通过协作、交叉施工及资源的调配后所具备的资源。

令工程按计划施工的人均平均速度

(11)

式中，Qi为工序i的工程量；Ti为工序i的持续时间；Yij为工序i的第j种职称的人数。

使用接力链技术进行施工时，考虑工序的难易程度、人员素质、人材机配合效率以及机械设备使用率等影响，得到工序i的人均施工速度

(12)

(13)

(14)

式中，ηi为工序i的综合能力指数；αi为工序i人员的平均素质；γi为资源储备系数；βi为工序i交叉施工时人材机配合的效率系数；D为工序的难易程度；M、N分别为设备的配备率和使用率；Eij为工序i的第j种职称权重，人员职称权值及权重分配如表1所示。

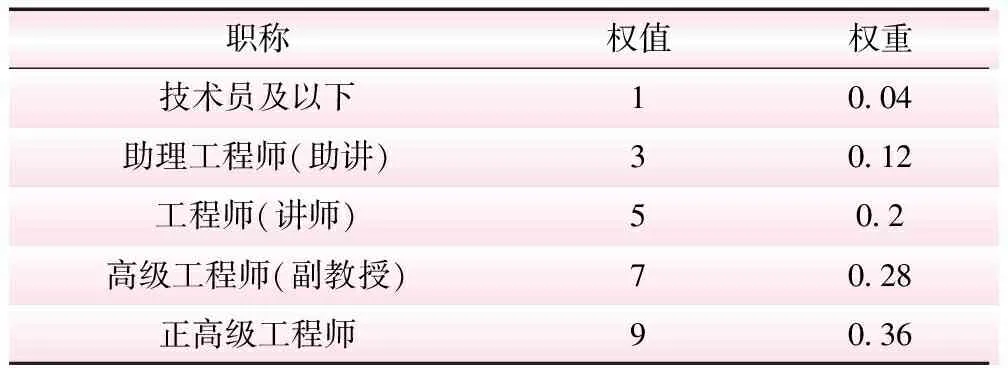
表1 人员职称权值及权重分配

4 缓冲区大小的计算

4.1 初始缓冲计算

第l条线路初始缓冲缓冲区bufferl为

(15)

式中，Pi为工序i的接力势。

4.2 非关键链汇入缓冲计算

令非关键链初始缓冲与非关键链最后一个工序的自由时差中的最小值计为汇入缓冲区，记第l条非关键链的汇入缓冲区的大小FBl，即

FBl=min(FFi，bufferl)

(16)

式中，FFi为工序i的自由时差。

4.3 非关键链剩余缓冲计算

令汇入缓冲与自由时差的差值(正值)为剩余缓冲，记为KB，第l条非关键路径的剩余缓冲KBl为

(17)

多条非关键路径汇入同一节点的剩余缓冲KB*为

KB*=max(KBl1，KBl2，…，KBln)

(18)

4.4 项目缓冲区大小计算

项目缓冲区PB计算公式为

(19)

式中，ll为项目的关键线路工序的集合。

5 实例分析

5.1 项目背景

某工程项目由A～I 9个工序组成，共4种资源，每个活动可能用到至少一种资源，各工作的时间参数及网络计划进度如图3所示，工序多目标因素相关参数如表2所示。

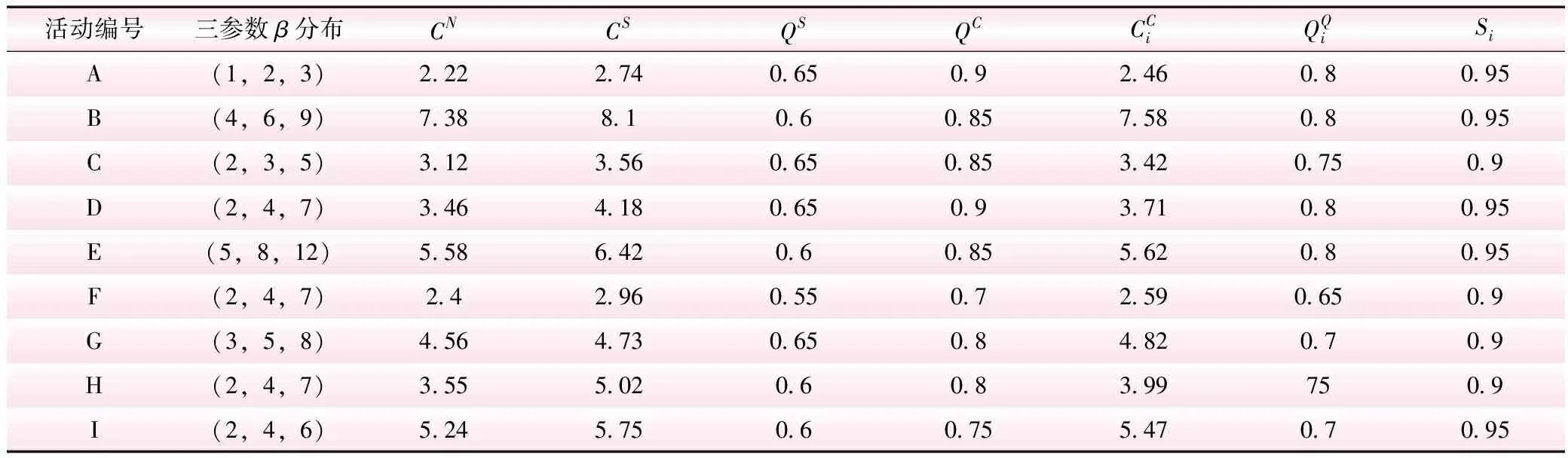
表2 工序多目标因素相关参数

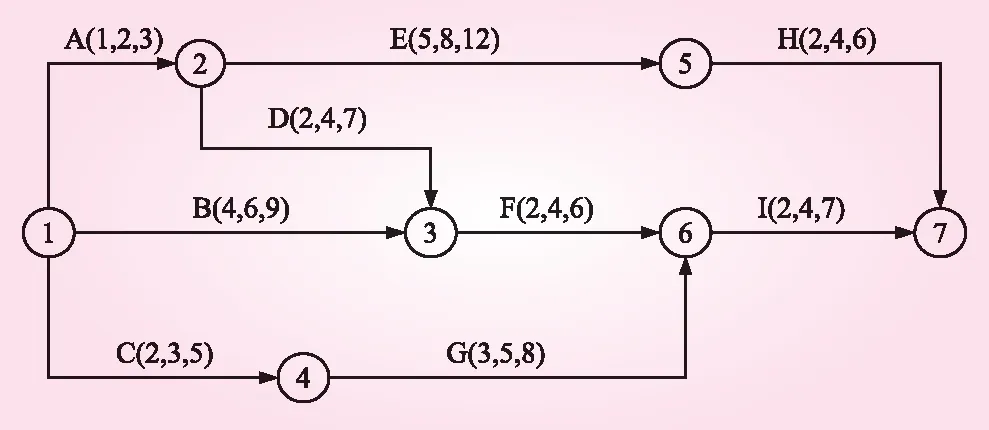
图3 网络进度计划

5.2 确定关键路径

5.2.1多目标约束下关键路径

对该项目各工序使用Beta(B)PERT分布进行蒙特卡罗仿真模拟，抽取10 000次仿真结果，得到每

个工序的时间参数输出结果，记T50%为每个工序的正常持续时间，以D工序为例，D工序的PERT分布图如图4所示，D工序正常持续时间为4.12 d，确定关键路径为A-D-F-I。

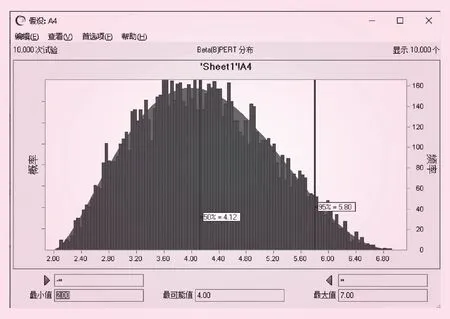
图4 D工序PERT分布模拟仿真

5.2.2多资源约束下关键路径

该项目活动受到4种资源限制，经式(8)～(10)计算得4种资源约束下各工序的资源影响系数，4种资源的受限系数εl为(0.43，1，0.5，0.25)，资源限量Rl为(8，1，2，4)，以A工序为例，计算得A的资源影响系数RIA=1.47，同理，计算其他工序的资源影响系数。关键路径为B-A-D-E-I，项目工期为24.48 d，资源影响系数计算结果如表3所示。

表3 资源影响系数计算

5.3 缓冲区大小计算

5.3.1工序安全时间计算

以A工序为例，在成本、质量以及安全3个目标约束下，令μi=0.6，由式(1)～(7)得：k1=-0.52，TAC=1.37 d；k2=0.25，TAQ=2.16 d；TAS=2.58(d)。A的最可能持续时间为Z1=max {2.49，2.32，2.58} =2.58(d)；工序A安全时间ST1=2.58+2.62-2×2.01=1.18(d)；在成本、质量、安全3个目标约束下的各工序安全时间计算如表4所示。

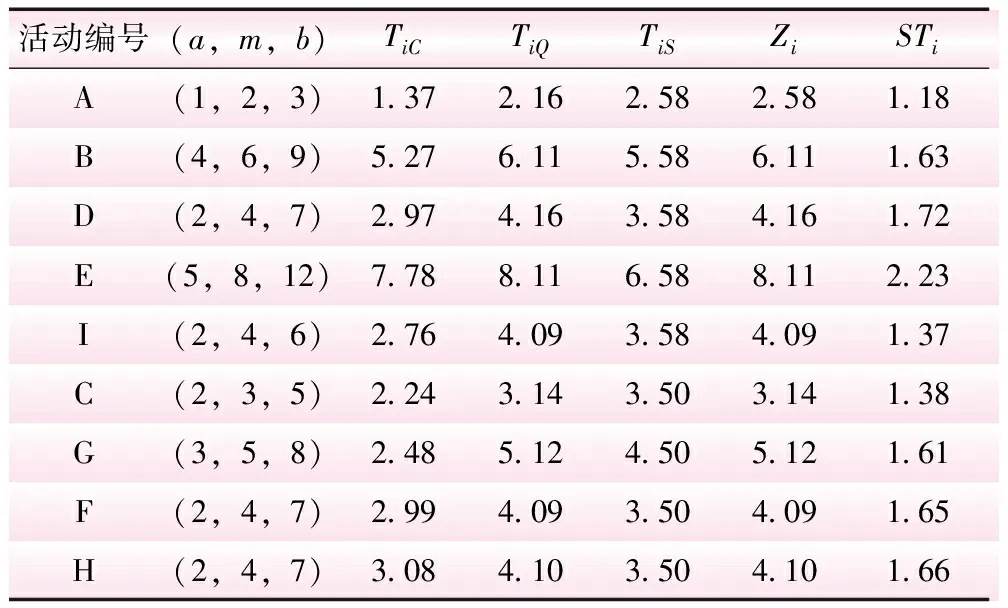
表4 多目标约束下工序时间计算 d

5.3.2工序接力势的计算

以工序D和G为例，关键链上工序D和非关键链上的工序G都为节点5的紧前工作。工序D人员配备为高级工程师1名，技术员3人；工序G人员配备为高级工程师1名，工程师1名，助理工程师2名，技术员1名；交叉施工时人材机的配合效率系数βD=0.95，βG=0.9；工序E、F的设备配置率MD=MG=0.99；工序难易程度DD=0.95，DG=0.8；资源储备系数γ=0.98；设备使用率ND=0.95，NG=0.9；E、F工序计划时间TD=3.13 d，TG=5.13 d；由式(11)～(14)得该项目接力网络平

均速度v=1.94，其中vD=2.45，vG=2.07。由“vD>vG>v，TD

由此计算各工序接力势，接力势网络进度计划如图5所示。